Brendan O’Connor
Symbolic Systems 205, Spring 2005
Systems, Theory and Metaphor
Instructor: Todd Davies
Simulation versus analytic methods:
a computational game theory story of Hope and Disillusionment
In their extended study/manifesto Growing Artificial Societies: Social Science from the Bottom Up, Joshua Epstein and Robert Axtell argue a simulations methodology is essential for researchers to study the emergence and network effects prevalent throughout social phenomena. They illustrate a series of intriguing experiments in “Sugarscape,” a simulated world of agents moving and interacting on a grid. Epstein and Axtell experiment with resource competition, trade, cultural transmission, pathogens, and other aspects of social systems.
Frustratingly, however, they often refrain from relating their work to existing analytic results and findings. While not as bad as the Stephen Wolfram’s egotistical soapbox A New Kind of Science, it sometimes seems that they neglect the rigor and intellectual merit of existing knowledge. Instead of challenging specific theories and findings from the literature, they make sweeping summaries of entire academic disciplines and then proceed to proclaim they do it differently and better. Instead of being its own discipline with its own rules, and findings (and therefore limited impact on the greater academic community), simulation as a science methodology should speak directly to the problems and engage the current answers that have been found with non-simulation techniques.
To that end, I have been interested in exploring simulation methodology and economic game theory, a field with a tremendous body of analytic findings. In this paper, I will describe a question about the behavior of a stochastic game theory learning process that I recently addressed in an exam question. (For Organizational Behavior 686 / Political Science 365, “Organizational Decision Making”, Jonathan Bendor.) First, using my intuitions and some standard analytic/classical game theory tools, I gave a verbal argument for what the behavior would be; I subsequently analyzed the question through computer simulation. In this paper I will present (with modifications) those analyses, and then examine it as an example of analytic versus simulation for scientific reasoning.
The problem
Consider two agents playing a game similar to a prisoners’ dilemma:[1] with simultaneous moves for the following payoff matrix, x > z > w > y.
|
|
D |
C |
|
D |
w,w |
x,y |
|
C |
y,x |
z,z |
Each agent has a strategy – a probability distribution over actions. For player i, their strategy is described by p_i, the probability to cooperate (move down, move right). The players play the game many times in sequence.
The agents each adjust their strategy through a simple satisficing process. Agent i has an aspiration level a_i. If i’s payoff PI_i exceeds its aspiration level, it then satisfices, doing two things: (1) it revises its strategy to increase the propensity to choose the action it just performed, and (2) it raises its aspiration level. If i’s payoff underperforms (is lower than its aspiration level), then it searches, decreasing its propensity to choose the action it just performed, and lowering its aspiration level. It is thought that this is a heuristic used for real-world decision-making, e.g. XXX Simon, March
The question asks what will happen if aspirations change via the Cyert-March update rule:
a_i,t+1 = lambda * a_i,t + (1 – lambda) * PI_i,t
The new aspiration is at a midpoint (weighted average)
between the old aspiration and the just-received payoff. The parameter lambda controls how fast the
updating happens.
The details of how the strategy shifts as a result of satisficing or search are left ambiguous.
The verbal analytic
approach
My initial intuitions were that the system would converge towards the Nash equilibrium. Here were my verbal intuitions:
The following diagram illustrates
the unilateral best moves at each state (pointing to the best reply against the
other’s move.)
D C
D w,w <-- x,y
^ |
| v
C y,x --> z,z
I argue the satisficing process
with weighted average aspiration adjustment will tend to follow these best
reply arrows.
Whatever the strategy update
rule is, assume no boundary cases, so you can’t get stuck on p_cooperate = 1.0
and never explore the D strategy.
Then, each player’s strategy mix
(probability distribution) will weigh more and more heavily toward D, which
provides a better payoff than C no matter what the opponent does.
possible
payoffs if opponent plays D: w vs.
y ==> D is better move
possible
payoffs if opponent plays C: x vs.
z ==> D is better move
First assume the other player
holds their move constant. If your
aspiration level is higher or lower than either payoff, it will eventually be
brought between them. In that case, you
will tend to satisfice on D and search on C.
Now let the other player switch back
and forth as well. This complicates
things since your aspiration can fluctuate a lot when they switch which column
you’re playing in. [imagine that lambda
is almost 1, so aspirations change minimally each round. this makes it easier to think about, but
hopefully the analysis should generalize to any lambda.] If your aspiration gets to the between
region of either payoff pair, it will tend to stick near the upper payoff,
since you’ll search on C but satisifice on D, thus spending more time on D.
Both players are following this pattern, so both end up playing a more and more of D.
This verbal description notes some mathematical facts and makes decently logical inferences, but it doesn’t completely solve the problem. Here’s one possibility it doesn’t consider: what if both players switch to cooperation at the same time? Isn’t it possible for their aspirations to simultaneously increase to match that, and therefore stay up there? What happens on the diagonal moves not seen in the best-reply graph? I don’t think this can be easily answered via verbal theory. Mathematical theory would be best, but seems (to me at least) difficult for this problem. Therefore, I tried testing this theory via simulation.
Simulation details for aspects underspecified in the original problem:
(1) I never allowed pure strategies, so some exploration was always forced. If agents can fall into pure strategies, then it’s possible to have low aspirations and get stuck on (C,C) because neither agent ever tries the better move D.
(2) Changes in an agent’s strategy are linear: searching and satisficing either increment or decrement p_i by a constant amount.
Results:
The results are heavily dependent on the lambda parameter in the update rule. The results are not so dependent on initial aspirations, or initial strategies. This is useful, at least for me: I had little intuition about what different lambda values would do to the stochastic process when writing that verbal theory.
High lambda = adjust aspirations very slowly. If aspirations adjust slowly (are very stable), things tend to settle around Nash – the prediction of the verbal analysis above. If aspirations adjust quickly (are unstable), things kind of settle near cooperation (pareto optimality) – violating the verbal argument’s assumption that the process generalizes to any lambda value.
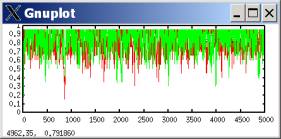
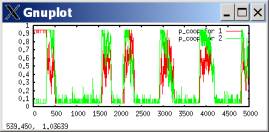
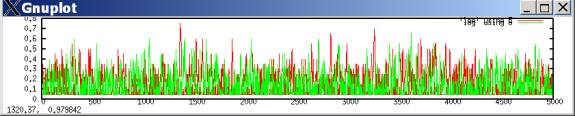
If aspirations adjust very slowly, they tend to stabilize around the mutual defection payoff (the (D,D) payoff of (w,w)). The following plots both agents’ aspiration levels with lambda=.99 with w=1 and z=2 (the payoffs for mutual defection and cooperation, respectively.) Most of the time, the agents expect (aspire to) mutual defection, but occasionally during outbreaks of cooperation their aspirations can temporarily rise to expect mutual cooperation.
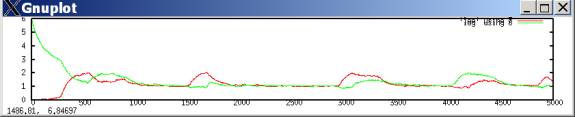
(here, aspirations started at greatly differing levels. However, starting aspirations at high, low, or in-between levels makes no difference to the long-run behavior.)
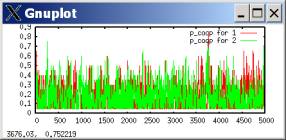
In such a case, defection tends to predominate, with occasional outbreaks of cooperation. These outbreaks occur when both players luckily explore cooperation and get higher aspirations; they then keep searching for a while, allowing some cooperation moves, until eventually better-paying defection tends to win out. The following plots the probability of a cooperate move for each player during the same simulation run.[2]

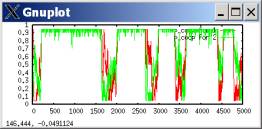
However, if aspirations update extremely fast, then the whole system is much more chaotic (randomly moving), BUT cooperation is more common.
For lambda=0.01:
The plot of aspiration levels is all over the map! Aspirations zoom from minimum to maximum levels quite readily.
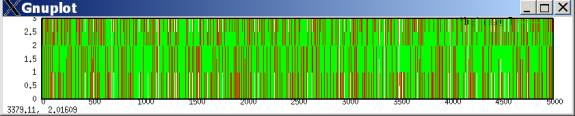
Plot of cooperation propensities: manages to be predominantly cooperative, though not really at a clear equilibrium. I even tried starting both players with 90% defection strategies, but still got predominant cooperation:
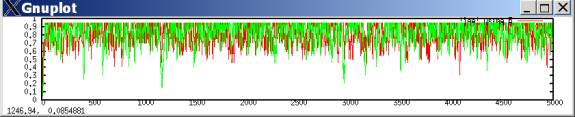
[The above graph, zoomed in at t<170. At beginning, cooperation takes off:

]
Finally, similar results can be obtained with quite high lambda values. Cooperation propensities for lambda=0.8:

Further, the results still hold if the exploiter’s x payoff is really high, and mutual cooperation is very bad in comparison. The previous graphs all used (x,z,w,y) = (3,2,1,0). The following uses (3, 0.2, 0.1, 0) and lambda=.01:

Why doesn’t this settle on Nash? My explanation is, every once in a while, both players try cooperation, then raise their aspiration levels up to, or close to, w. If they both move off to mutual defection, that is no longer satisfactory, so will keep searching. If one moves off to the sucker’s payoff, that is not satisfactory, so will search back to mutual cooperation.
Game structure
The structure of the game is very important to a stochastic search process around strategies, thus the payoff ordering tends to be important. For the above analysis, what’s important is that w>x and y>z, and that w>z.
If we violate w>z and make the mutual-C payoff worse than the mutual-D payoff, of course the flexible aspiration model can’t sustain C moves at all. Mutual defection now dominates mutual cooperation, so when both sides accidentally get mutual cooperation, aspirations don’t rise to attract them there. For y,z,w,x = 3,2,1,0, both the slow-aspiration Nash-like and fast-aspiration pareto-like equilibriums are now for defection:
lambda=.99 [slow adjustments], cooperation propensities
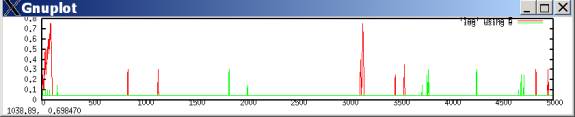
(also note: the defection equilibrium is much stronger than the slow-adjustment version in the PD)
lambda=.01 [fast adjustments], cooperation propensities
Relevance of these
results for theories of decision-making
The Nash equilibrium, seemingly founded upon such odd ideas of unboundedly rational iterated strategy deletion and the like, is actually useful to predict results in a world of bounded rationality (BR): a satisficing learning process can converge on an NE. It does so for the same reason that NE’s are predicted in unboundedly rational decision-making: it doesn’t pay for either player to unilaterally move away from an NE. Therefore, low-memory satisficing can move towards more rational outcomes.
However, BR can display quite complex complicated behavior. A multi-agent BR system can get to equilibriums that aren’t Nash.
There also are implications for the study of cooperation. For the most problematic social-dilemma cases of cooperation like the PD, BR can learn through a repeated game to settle, or kind-of-settle, on an efficient cooperative outcome.
What’s extremely interesting is that fast-moving aspirations got the system tending towards the pareto solution of mutual cooperation. Is this because mutual cooperation is pareto optimal, or is it for other reasons in the structure of the PD? This would be good to further investigate; a relationship between BR and pareto optimality would be good to know, because it would have implications for the study of cooperation and social welfare.
The code for the simulation
Language: python, which is open source and also quite readable. I had problems with bugs for a while, but seem to be solved now. The program simply outputs values as a table of numbers, which can be graphed with a variety of programs; I used Gnuplot.
import random
# x > z > w > y
x,z,w,y = 3,2,1,0
#x,z,w,y = 3, .2, .1, 0
# alternative suggested in part [3]
#y,z, w,x = 3,2,1,0
## for moves, 0 means up, 1 means down
def payoffs(move1, move2):
global
x,z,w,y
if move1
== 0 and move2 == 0:
return w,w
if move1
== 1 and move2 == 0:
return y,x
if move1
== 0 and move2 == 1:
return x,y
if move1
== 1 and move2 == 1:
return z,z
#aspirations
a1, a2 = 0,6
#strategies: prob move down
p1,p2 = .9, .1
def choose_down_with_prob(p):
if
random.random() < p:
return 1
else:
return 0
### cyert-march weighted average updating of
aspirations
lmbda = 0.99
def update_aspir(a, payoff):
global
lmbda
return
lmbda* a + (1-lmbda)* payoff
### strategy updating
### stepwise update rules as in part (a) of the
problem
### we want to always allow possibility of
exploring, so no 1.0 or 0.0 allowed
delta_p = 0.05
def update_strat(p, a, payoff, move):
if payoff
>= a: return update_p_via_satisfice(p, move)
if payoff
< a: return update_p_via_search(p,
move)
## move toward what you just did
def update_p_via_satisfice(p, move):
if move
== 1: return move_p_down(p)
if move
== 0: return move_p_up(p)
## move away from what you just did
def update_p_via_search(p, move):
if move
== 1: return move_p_up(p)
if move
== 0: return move_p_down(p)
### these don't allow 0.0 or 1.0 probabilities
# the .000001 crap solves for weird floating point
arithmetic rules/bugs
def move_p_up(p):
global
delta_p
if p <
1-delta_p -.0000001:
return p + delta_p
return p
def move_p_down(p):
global
delta_p
if p >
delta_p +.0000001:
return p - delta_p
return p
### main loop
for iter in xrange(5000):
move1 =
choose_down_with_prob(p1)
move2 =
choose_down_with_prob(p2)
payoff1,
payoff2 = payoffs(move1, move2)
p1 =
update_strat(p1, a1, payoff1, move1)
p2 =
update_strat(p2, a2, payoff2, move2)
a1 =
update_aspir(a1, payoff1)
a2 =
update_aspir(a2, payoff2)
print
"%s %s %s %s %s %s
%s %s" %(move1,move2, payoff1,payoff2, p1,p2, a1,a2)
Reflections
For this particular problem, I found simulations invaluable for testing my
intuitions and teasing apart assumptions in my verbal analysis. While it’s true that I didn’t spend
extensive time trying verbal or even mathematical analysis of the problem, I’m
not sure that I could have reached the conclusions I did without the help of
simulation.
Simulations seem to be most valuable for this sort of strictly theoretical work when they are as simple as possible. Writing, running, and analyzing the simulation results took about 4 hours total. A good portion of that time was writing and debugging the program; several times I found results opposite of what I expected, only to find I had accidentally reversed the signs on the increment calculation, ran into the oddities of Python/C floating point arithmetic, or other bugs. After spending a lot of time pouring over this short program, I am now reasonably certain it isn’t buggy, and that my results are real. If the simulation was much more complex, I would have a very hard time convincing myself of its correctness.
Simulation was most valuable as an intermediate aid to verbal analysis. Using simulation, I found a discrepancy in
behavior of fast- versus slow-moving aspirations. Analyzing the results, I found a verbal explanation for the
discrepency.
Trouble...
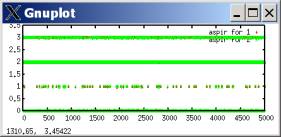
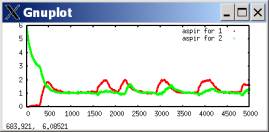
The fact that it’s so easy to find new reasons behind the data gives one pause, however. If arguments are easy to come by, how do you know that any of them are actually true? When re-examining the results, I was curious how the outbreaks of cooperation in the slow-adjusting case (lambda=.99) could ever happen. With a typical simulation run, I analyzed an outbreak of cooperation.
Cooperation propensities:

Zoomed in on the outbreak of cooperation at t=1000. Remember: payoffs are 3,2,1,0.
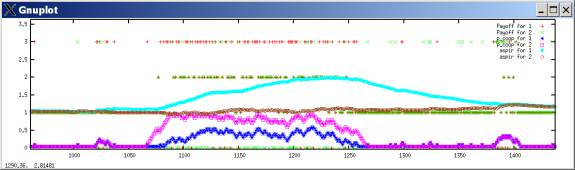
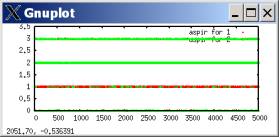
Agent 2 somehow gets suckered in to becoming more cooperative around t=1070. Now, during the usual defection-dominated periods, whenever and agent tries cooperation, they get punished with a 0 sucker’s payoff, which always is less than their aspiration, and so they are reinforced against cooperation. However, now that Agent 2 is cooperative, Agent 1 exceeds aspirations with cooperation. It’s true that it does better exploiting than cooperating, but both actions exceed aspirations. Thus it is possible for Agent 2 to become more cooperative, though not unreservedly so.
But why does Agent 2 ever start cooperating in the first place? A closer analysis is puzzling.
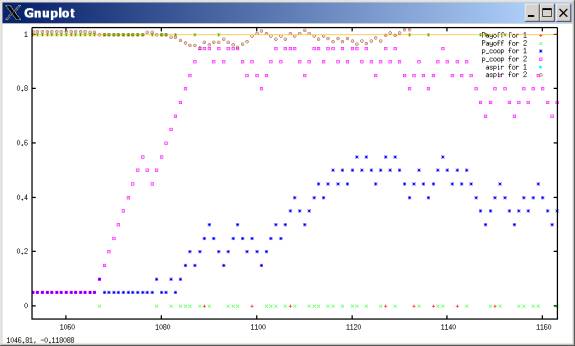
At round 1068, it plays C and is exploited. Its aspiration lowers very slightly, dipping below 1.0. This seems to be the trigger for a sudden increase in cooperation propensity. During the ascent of Agent 2’s cooperativeness, both sides are playing mutual defection like usual. However, for Agent 2, we would expect the OPPOSITE effect: the mutual defection outcome now satisfies 2’s aspirations! If you’re defecting, and defecting is satisfactory, then you should increase your propensity to defect. We should expect an opposite pattern: when aspirations are above 1.0, mutual defections should reinforce propensity to cooperate, while when aspirations are below 1.0, mutual defections should reinforce propensity to defect.
In fact, we would expect right. Those 90 short lines of code have a terrible bug: the learning logic is reversed, due to a confusing use of the terms “up” and “down.” move_p_up() increments the value of p upwards by delta_p. However, the code identifies p as the probability of a down movement. The caller of the move_p_up/down() functions are the update_p_via_satisfice/search() functions, which use “up” and “down” as identifiers for the direction of movement. These meanings are opposite, and this is an error.
The origins of this error stem from the original formulation of the problem, which described the payoffs without the “cooperate” and “defect” labels, and without any mention of the PD or cooperation games. The code was originally written only with abstract up and down moves; calling them defection and cooperation was a later innovation.
Error fixed
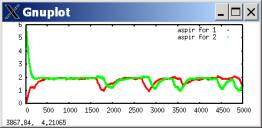
I fixed the error in the move_p_up/down() functions, and all the results from the previous section were completely reversed. Fast-moving aspirations tend to all-defection, and slow-moving aspirations tend toward cooperation.
lambda=0.1 (fast-moving aspirations)
WRONG: RIGHT:
cooperation propensities
|
|
|
|
|
|
aspirations
lambda=0.99 (slow-moving aspirations)
WRONG: RIGHT:
cooperation propensities
|
|
|
|
|
|
aspirations
Reflections
To say the least, it’s pretty disturbing that all of the big verbal analysis I did was completely wrong. In fact, the truth is often OPPOSITE of what I concluded.
This bug is really simple: just a question of direction. It would have been easier to avoid had I spent more time analyzing the problem – for example, determining what sorts of movements should happen given different aspiration levels. That was the sort of analysis I needed to do to discover the programming error in the first place. Once that analysis is done, it’s easy to set up parameters in the code and test to make sure the expected behavior happens. Only once you’re certain that the code is functioning as expected, is it safe to move to full-fledged simulation.
Maybe I’m just a sloppy programmer, and this play-it-safe methodology is an overreaction. However, it seems reasonable to think it at least somewhat necessary. The enterprise of software development in general is infamous for the indeterminacy and prevalence of bugs and problems in computer code. It is very difficult to know if problems exist, or where they are, or in what conditions things will not work correctly. If it’s the case that bugs are a big problem –that is, they often exist and cause unwanted aberrations in program behavior – then this is a huge problem with simulation science methodology, since it casts doubt on your simulations results, especially for more complex simulations. Even if scientists are careful to document their code make it public for peer review, it seems unlikely that it will receive rigorous scrutiny. And the experiences of software development seem to indicate that without rigorous scrutiny & testing, computer code tends to be buggy ... and if the code could be buggy, you can’t trust any of the results.
Hopefully it’s possible for a tradition of rigorous software engineering to develop for simulation science, much like how most sciences have a tradition & widespread training in statistics. Robert Axelrod advocated features like this in his “Advancing the State of Simulation Science,” where he argued for using common software platforms and reproducible experiments. This may be necessary to prevent a future scandal when some major simulation study gets discredited due to bugs or arbitrary features in its code. (E.g. Huberman & Glance (1993)[3]: they re-ran some space/time-embedded PD simulations and found dramatic differences in results when changing seemingly unimportant details of the granularity of space and time.) If you want to be sure that simulation methodology isn’t just the interpretation of artificial results, progress needs to be made in this direction.