Large Deviations for the Empirical Mean of an M/M/1 Queue
J. Blanchet , P. W. Glynn, and S. Meyn
Queueing Systems: Theory and Applications, Vol 73, No. 4, 425-446 (2013)
Let 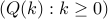 be an M/M/1 queue with traffic intensity
be an M/M/1 queue with traffic intensity 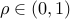 . Consider the quantity
. Consider the quantity
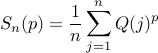
for any 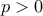 . The ergodic theorem yields that
. The ergodic theorem yields that ![S_n(p)to mu(p):= E[Q(infty)p]](eqs/9041184216064832473-130.png) , where
, where 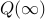 is geometrically distributed with mean
is geometrically distributed with mean 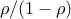 . It is known that one can explicitly characterize
. It is known that one can explicitly characterize 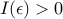 such that
such that
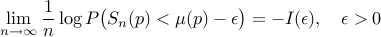
In this paper, we show that the approximation of the right tail asymp-totics requires a different logarithm scaling, giving
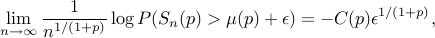
where 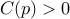 is obtained as the solution of a variational problem.
is obtained as the solution of a variational problem.
We discuss why this phenomenon — Weibullian right tail asymptotics rather than exponential asymptotics — can be expected to occur in more general queueing systems.