On the Convergence of Finite Order Approximations of Stationary Time Series
S. D. Gupta, R. R. Mazumdar, P. W. Glynn
Journal of Multivariate Analysis Vol. 121, 1-21,(October 2013),
The approximation of a stationary time-series by finite order autoregressive (AR) and moving averages (MA) is a problem that occurs in many applications. In this paper we study asymptotic behavior of the spectral density of finite order approximations of wide sense stationary time series. It is shown that when the on the spectral density is non-vanishing in ![[-pi,pi]](eqs/8740547434289145383-130.png) and the covariance is summable, the spectral density of the approximating autoregressive sequence converges at the origin. Under additional mild conditions on the coefficients of the Wold decomposition it is also shown that the spectral densities of both moving average and autoregressive approximations converge in
and the covariance is summable, the spectral density of the approximating autoregressive sequence converges at the origin. Under additional mild conditions on the coefficients of the Wold decomposition it is also shown that the spectral densities of both moving average and autoregressive approximations converge in 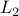 as the order of approximation increases.
as the order of approximation increases.