ADMM

The alternating direction method of multipliers (ADMM) is an algorithm that solves convex optimization problems by breaking them into smaller pieces, each of which are then easier to handle. It has recently found wide application in a number of areas. On this page, we provide a few links to to interesting applications and implementations of the method, along with a few primary references.

ADMM is used in a large number of papers at this point, so it is impossible to be comprehensive here. We only intend to highlight a few representative examples in different areas. To keep the listing light, we have only listed more detailed bibliographic information for papers that are not easy to find online; in any case, the information given should be more than enough to track down the papers.

Main references

Distributed optimization and statistical learning via the alternating direction method of multipliers: S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, 2011
Proximal algorithms: N. Parikh and S. Boyd, 2014

Software

Classic papers

On the numerical solution of heat conduction problems in two and three space variables: J. Douglas and H. H. Rachford, Transactions of the American Mathematical Society, 1956

Sur l'approximation, par éléments finis d'ordre un, et la résolution, par pénalisation-dualité d'une classe de problèmes de Dirichlet non linéares: R. Glowinski and A. Marrocco, Revue Française d'Automatique, Informatique, et Recherche Opérationelle, 1975

A dual algorithm for the solution of nonlinear variational problems via finite element approximations: D. Gabay and B. Mercier, Computers and Mathematics with Applications, 1976

Splitting algorithms for the sum of two nonlinear operators: P. L. Lions and B. Mercier, 1979

On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators: J. Eckstein and D. Bertsekas, Mathematical Programming, 1992

Generic problems

Alternating direction augmented Lagrangian methods for semidefinite programming: Z. Wen, D. Goldfarb, and W. Yin, 2010
Block splitting for distributed optimization: N. Parikh and S. Boyd, 2014
Operator splitting for conic optimization via homogeneous self-dual embedding: B. O'Donoghue, E. Chu, N. Parikh, and S. Boyd, 2014

Applications

Robust Principal Component Analysis?: E. J. Candès, X. Li, Y. Ma, and J. Wright, 2009
An alternating direction method for dual MAP LP relaxation: O. Meshi and A. Globerson, 2011
An augmented Lagrangian approach to constrained MAP inference: A. Martins, M. Figueiredo, P. Aguiar, N. Smith, and E. Xing, 2011
Dual decomposition with many overlapping components: A. F. T. Martins, N. A. Smith, P. M. Q. Aguiar, and M. A. T. Figueiredo, 2011
Decomposition methods for large scale LP decoding: S. Barman, X. Liu, S. Draper, and B. Recht, 2011
Scaling MPE inference for constrained continuous Markov random fields with consensus optimization: S. Bach, M. Broecheler, L. Getoor, and D. O'Leary, 2012
Distributed robust multicell coordinated beamforming with imperfect CSI: an ADMM approach: C. Shen, T.-H. Chang, K.-Y. Wang, Z. Qiu, and C.-Y. Chi, 2012
Design of optimal sparse feedback gains via the alternating direction method of multipliers: F. Lin, M. Fardad, M. R. Jovanovic, 2013
Tensor completion for estimating missing values in visual data: J. Liu, P. Musialski, P. Wonka, J. Ye, 2013
A lasso for hierarchical interactions: J. Bien, J. Taylor, and R. Tibshirani, 2013
Statistical estimation and testing via the sorted 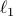norm: M. Bogdan, E. van den Berg, W. Su and E. J. Candès, 2013
The joint graphical lasso for inverse covariance estimation across multiple classes: P. Danaher, P. Wang, and D. Witten, 2013
Distributed robust power system state estimation: V. Kekatos and G. B. Giannakis, 2013
A splitting method for optimal control: B. O'Donoghue, G. Stathopoulos, and S. Boyd, 2013
Dynamic network energy management via proximal message passing: M. Kraning, E. Chu, J. Lavaei, and S. Boyd, 2014

Theory and variations

On the 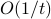convergence rate of the Douglas-Rachford alternating direction method: B. He and X. Yuan, 2012
Fast alternating direction optimization methods: T. Goldstein, B. O'Donoghue, S. Setzer, and R. Baraniuk, 2012
Augmented Lagrangian and alternating direction methods for convex optimization: a tutorial and some illustrative computational results: J. Eckstein, 2012