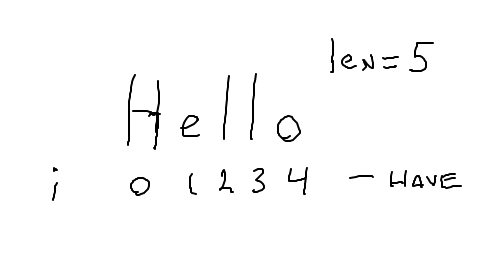
Today: Idiomatic phrases, "reverse" chronicles, Better/shorter code invariant, more string functions, unicode

Today - Better / Shorter / Cleaner

Today, I'll show you some techniques where we have code that is already correct, but we can write it in a better, shorter way. It's intuitively satisfying to have a 10 line thing, and shrink it down to 6 lines that reads better.

Technique: Build on Idiomatic Phrases

You can think of every program as having some phrases of stock, idiomatic code, and then some phrases that are custom, idiosyncratic bits particular to that algorithm. We'll just say, use the idiomatic bits where they come up — easy to type in, easy to understand. Build your needed changes around the idiomatic code. The first 3 reverse() solutions below work in this way.

The "Reverse" Rosetta Stone

> Reverse problems

How many ways can you think of to reverse a string in Python? A sort of parlor trick to see a series of python techniques worked out, compare them.

'Hello' -> 'olleH'

Aside: there is a scene in the Movie Amadeus where Motzart plays a piece one way, then gets under the piano, reaches hands up and plays it again upside down. I believe today this would be called a "flex"? In any case, it is reminiscent of the problem here of taking the normal thing and dong it backwards. youtube

reverse1() - Muggle i_rev

We are very familiar with the idiomatic for i in range(len(s)), running i through the index numbers from start to end: 0, 1, 2, ... len-1. Start with that idiomatic loop. Think about computing an i_rev from each i, which will go through the string backwards: the last char, then the next to last, and so on. There turn out to be easier ways, but this is a reasonable approach.

I think of this as the "muggle" solution - using intricate devices to get the effect where there are easier ways. We could give this full credit, possibly pointing out the easier ways to do it.

Sketch out the idea on this drawing

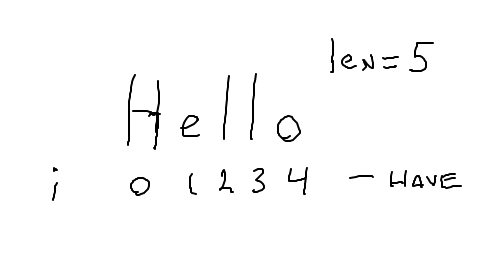
alt: s with regular index i

Something like this:

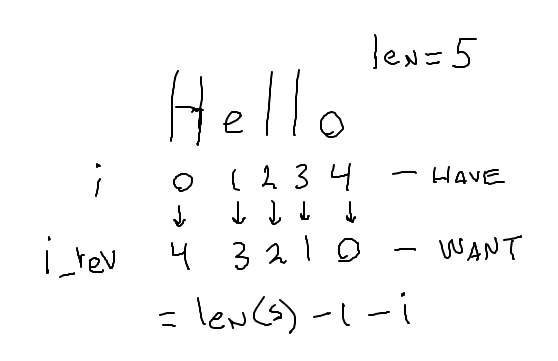
alt: compute i_rev for each i into s

reverse2() - reversed()

Using the well known, idiomatic for i in range(len(s)) is a good idea. The reversed() function is less well known, yielding a sequence in reverse order, but here it solves the problem very neatly.

reverse3() - +=

There's a very neat way to solve this using just the plain old for ch in s loop. Think about how you might re-write the += line. This is perhaps the most elegant, if non-obvious, solution, as it is short and uses simple Python features.

reverse4() - while

Instead of reversed() and range(), could write a while loop to manually generate the index numbers in the order we want. This is no longer a great solution - doing manually something that range() and reversed() provide for free.

reverse5 and reverse6

These are more silly uses of Python techniques, although they are code patterns we will cover later in CS106A, so we can check these out then.

Technique: Better/Shorter Code with Invariant

> Better problems

Suppose we have
Some lines for case-1
Other lines for case-2
"Invariant" = condition is true about a line for all cases
Fix things so 1 set of lines
the lines handle all cases
vs. separate lines for each case
In these examples, use a variable to make lines work for all cases

speeding() Example

speeding(speed, birthday): Compute speeding ticket fine as function of speed and birthday boolean. Rule: speed under 55, fine is 100, otherwise 200. If it's your birthday, the allowed speed is 5 mph more. Challenge: change this code to be shorter, not have so many distinct paths.

The code below works correctly. How to write it better/shorter? How are the if-lines different?

def speeding(speed, birthday):
    if not birthday:
        if speed < 50:
            return 100
        else:
            return 200
    else:  # is birthday
        if speed < 55:
            return 100
        else:
            return 200

Invariant Var Solution

These lines look really similar
They differ by the value in the if-test
Solution: introduce "limit" variable
limit holds the value that distinguishes 100/200 fines
Code can adjust limit up/down
Don't need 2 if-statements
Use 1 if-statement that uses limit
Summary
Used to have if-stmt1 and if-stmt2
Set a variable above that lets one if-stmt handle both cases
Minor: Can write without else, "pick off" return style

speeding() Better Solution

def speeding(speed, birthday):
    # Setup limit var
    limit = 50
    if birthday:
        limit = 55
    
    # Invariant: limit holds value to use
    if speed < limit:
        return 100
    return 200

Tradeoff: we're adding a variable to remove an if-statement

ncopies() Demo/Exercise

Change this code to be better / shorter. Look at lines that are similar - make an invariant.

ncopies(word, n, suffix): Given name string, int n, suffix string, return n copies of string + suffix. If suffix is the empty string, use '!' as the suffix. Challenge: change this code to be shorter, not have so many distinct paths.

Before:

def copies(word, n, suffix):
    result = ''
    
    if suffix == '':
        for i in range(n):
            result += word + '!'
    else:
        for i in range(n):
            result += word + suffix
    return result

ncopies() Better Solution

Solution: use logic to set "suffix" to hold the suffix to use for all cases. Later code just uses suffix vs. separate if-stmt for each case.

def copies(word, n, suffix):
    result = ''
    # Set suffix to be value to use regardless
    if suffix == '':
        suffix = '!'
 
    # invariant: suffix is value to use
    for i in range(n):
        result += word + suffix
    return result

String - More Functions

See guide for details: Strings

Thus far we have done String 1.0: len, index numbers, upper, lower, isalpha, isdigit, slices, .find().

There are more functions. You should at least have an idea that these exist, so you can look them up if needed. The important strategy is: don't write code manually to do something a built-in function in Python will do it for you. The most important functions you should have memorized, and the more rare ones you can look up.

s.startswith() s.endswith()

These are very convenient True/False tests for the specific case of checking if a substring appears at the start or end of a string. Also a pretty nice example of function naming.

>>> 'Python'.startswith('Py')
True
>>> 'Python'.startswith('Px')
False
>>> 'resume.html'.endswith('.html')
True

String - replace()

str.replace(old, new)
Returns a new string with replacements done (immutable)
Does not respect word boundaries, just dumb replacement
Anti-Pattern:
Given s to compute something
e.g. count the digits in s
Do not use replace() to modify s as a shortcut to computing about s
Not a good strategy

>>> s ='this is it'
>>> s.replace('is', 'xxx')  # returns changed version
'thxxx xxx it'
>>> 
>>> s.replace('is', '')
'th  it'
>>> 
>>> s        # s not changed
'this is it'

Recall: s.foo() Does Not Change s

Recall how calling a string function does not change it. Need to use the return value...

# NO: Call without using result:
s.replace('is', 'xxx')
# s is the same as it was


# YES: this works
s = s.replace('is', 'xxx')

String - strip()

Removes whitespace chars from either end
Use with for line in f to trim off \n

>>> s = '   this and that\n'
>>> s.strip()
'this and that'

String - split()

Nice feature to parse a line of text
e.g. from a file line 11,45,19.2,N
str.split() -> array of strings
str.split(',') - splits on ',' substring
str.split() - zero params
special
splits on 1 or more whitespace chars
combines multiple whitespace chars
handy primitive "word" from line feature

>>> s = '11,45,19.2,N'
>>> s.split(',')
['11', '45', '19.2', 'N']
>>> 'apple:banana:donut'.split(':')
['apple', 'banana', 'donut']
>>> 
>>> 'this    is     it  '.split()  # special whitespace form
['this', 'is', 'it']

String - join()

Reverse of split()
Given list of strings, puts them together to make a big string
Mnemonic: str.split() and str.join()
The string is the noun in noun.verb form

>>> foods = ['apple', 'banana', 'donut']
>>> ':'.join(foods)
'apple:banana:donut'

String - format()

You have a string and want to paste values into it
str.format() does this
The marker {} marks where to paste in
Simple first way: use + and str(12) to assemble string

>>> 'Alice' + ' got score:' + str(12)  # old: + and str()
'Alice got score:12'
>>>
>>> '{} got score:{}'.format('Alice', 12) # new: format()
'Alice got score:12'
>>>

String Unicode

In the early days of computers, the ASCII character encoding was very common, encoding the roman a-z alphabet. ASCII is simple, and requires just 1 byte to store 1 character, but it has no ability to represent characters of other languages.

Each character in a Python string is a unicode character, so characters for all languages are supported. Also, many emoji have been added to unicode as a sort of character.

Every unicode character is defined by a unicode "code point" which is basically a big int value that uniquely identifies that character. Unicode characters can be written using the "hex" version of their code point, e.g. "03A3" is the "Sigma" char Σ, and "2665" is the heart emoji char ♥.

Hexadecimal aside: hexadecimal is a way of writing an int in base-16 using the digits 0-9 plus the letters A-F, like this: 7F9A or 7f9a. Two hex digits together like 9A or FF represent the value stored in one byte, so hex is a traditional easy way to write out the value of a byte. When you look up an emoji on the web, typically you will see the code point written out in hex, like 1F644, the eye-roll emoji 🙄.

You can write a unicode char out in a Python string with a \u followed by the 4 hex digits of its code point. Notice how each unicode char is just one more character in the string:

>>> s = 'hi \u03A3'
>>> s
'hi Σ'
>>> len(s)
4
>>> s[0]
'h'
>>> s[3]
'Σ'
>>>
>>> s = '\u03A9'  # upper case omega
>>> s
'Ω'
>>> s.lower()     # compute lowercase
'ω'
>>> s.isalpha()   # isalpha() knows about unicode
True
>>>
>>> 'I \u2665'
'I ♥'

For a code point with more than 4-hex-digits, use \U (uppercase U) followed by 8 digits with leading 0's as needed, like the fire emoji 1F525, and the inevitable 1F4A9.

>>> 'the place is on \U0001F525'
'the place is on 🔥'
>>> s = 'oh \U0001F4A9'
>>> len(s)
4

Unicode and Ethics

In the early days of computing in the US, computers were designed with the ASCII character set, supporting only the roman a-z alphabet. This hurt the rest of the planet, which mostly doesn't write in English. There is a well known pattern where technology comes first in the developed world, is scaled up and becomes inexpensive, and then proliferates to the developing world. Computers in the US using ASCII broke that technology pipeline. Ethically, realize that choosing a US-only solution makes the technology hard to access for most of the world - somewhere between unethical and ungenerous.

Unicode is a good solution for what it does - a freely available available standard. If a system uses Unicode, it and its data can interoperate with the other Unicode compliant systems - demonstrating the value created by a standard vs. having a bunch of incompatible systems.

Unicode vs. Moore's Law

There is something of an economic view to the transition from ASCII to unicode. In the 1950's every byte was literally expensive. An IBM model 360 could be leased for $5,000 per month and had about 32 kilobytes of RAM (not megabytes or gigabytes .. kilobytes!). A unicode character that required 2 or 4 bytes was quite unattractive if you could get away with 1 byte. Of Course Unicode had not been invented yet, and the price of RAM is part of why.

Say 30 years later when Unicode became more common. Using double-every-2-years Moore's law as an estimate, 30 years = 15 doublings.

>>> 2 ** 15
32768

So RAM is on the order of 32,000 times more prolific by the 1990s. The costs don't track Moore's law exactly, but that gives you the idea. Anyway, adopting Unicode was the ethical and efficient thing to do, allowing software, files etc. to work across languages and across the world. The plummeting price of the extra RAM required no doubt helped move things along.