Today: black box, string loops, Start movie example, grid, grid testing.

Black Box - Describing Code

Suppose there were a function named alpha_only(s), and we tried to describe it, talking about its code. Code has a lot of detail and complexity to it, so it's not a good way to characterize a function.

Black Box - Inputs and Outputs

Instead, we wall off the code, not looking inside the function. Instead, characterize the function by talking only about its input and output data - parameters and return value.

Black Box Design

• The Black Box "paradigm" works great for designing and combining functions
• A sort of design rule - the function looks only at its input parameters
  "Repeatable"
  Calling the function with the an input returns the same output every time
• Helps your own brain
  Imagine you are working a program of 10 functions
  Need to keep straight in your own mind what each function does
• Black box also works well for testing .. later today!

Strings

Continue with strings. For more details, see the Python guide chapter on strings

Useful Pattern: s = s + something

• Use + to add something at the end of a string, yielding a new bigger string
• Use = to assign the new string back to the original variable
• e.g. s = s + 'xxx'
• The += operator works here too
• We are constructing a new, bigger string with each step

>>> s = 'hello'
>>> s = s + '!'
>>> # Q: What is s now?

Answer: s is 'hello!' after the two lines. So s = s + xxx is a way of adding something to the right side of a string. The following form does the exactly the same thing using += as a shorthand:

>>> s = 'hello'
>>> s += '!'

String Index Numbers

Here is our string, using zero-based index numbers to refer to the individual chars..

>>> s = 'Python'
>>> s[0]
'P'
>>> s[1]
'y'
>>>

How To Loop Over Those Index Numbers?

The length of the string is 6. The index numbers are 0, 1, 2, 3, 4, 5. How to write a loop that generates those numbers? It's the same loop we used to, say, loop over the x values of an image. If the image width was 100, we wanted the index numbers 0, 1, 2.. 99. Strings are exactly the same, feeding len(s) into the range() function.

Standard loop: for i in range(len(s)):

This is the standard, idiomatic loop to go through all the index numbers. It's traditional to use a loop variable with the simple name i with this loop. Inside the loop, use s[i] to access each char of the string.

• The standard loop to go through all the index numbers
• e.g. s = 'Python'
• Length is 6
• Want index numbers 0, 1, 2, 3, 4, 5
• Recall range(n) goes 0 .. n-1
• So use range(6) aka range(len(s))
• for i in range(len(s)):
• Use s[i] to access each char in the loop
• Standard to use the variable name i for this loop
• This loop is so common, it's idiomatic
• We'll see another way to do this later

# have string s
for i in range(len(s)):
    # access s[i] in here

1. double_char() Example

double_char(s): Given string s. Return a new string that has 2 chars for every char in s. So 'Hello' returns 'HHeelllloo'. Use a for/i/range loop.

> double_char

Also, see the experimental server section string2 for many problems like double_char()

• Standard for/i/range loop to look at every char
• Initialize result = '' variable before loop
• Update in loop: result = result + xxxx
• Use s[i] to access each char in loop
• Return result at end
• Could use += shortcut
• Q: does it work on empty string input?

Solution code

def double_char(s):
    result = ''
    for i in range(len(s)):
        result = result + s[i] + s[i]
    return result

Extra: not_ab()

not_ab(s): Given string s. Return a new string made of all the chars in s which are not lowercase 'a' or 'b'. Use a for/i/range loop.

Try to solve using for/i/range loop with the += pattern like double_char(). Test each char to see if it is 'a' or 'b' using !=.

> not_ab

String Testing: 'a' vs. 'A'

We've used == already. 'a' and 'A' are different characters.

>>> 'a' == 'A'
False
>>> s = 'red'
>>> s == 'red'   # two equal signs
True
>>> s == 'Red'   # must match exactly
False

String Testing - in

• The word in - test if a substring appears in a string
• Mnemonic: same word inside for-loop, like Python wants to introduce very few new words
• Chars must match exactly - upper/lower are considered different

>>> 'c' in 'abcd'
True
>>> 'bc' in 'abcd'
True
>>> 'bx' in 'abcd'
False
>>> 'A' in 'abcd'
False

String Character Class Tests

• String is made of characters
• Categorize characters into major classes:
• 1. Alphabetic - 'a' 'Z' .. used to make words
• 2. Digits - '0' '2' .. used to make numbers
• 3. Space - space, tab, newline - aka "whitespace"
• There are noun.verb tests for the above 3, returning boolean True or False
• For empty string return False (a weird edge case)
• All the other chars form a miscellaneous class - '$' '%' ';' ... any char not in the first 3 categories

s.isdigit() - True if all chars in s are digits '0' '1' .. '9'

s.isalpha() - True for alphabetic word char, i.e. 'a-z' and 'A-Z'. Each unicode alphabet has its own definition of what's alphabetic, e.g. 'Ω' below is alphabetic.

s.isalnum() - alphanumeric, just combines isalpha() and isdigit()

s.isspace() - True for whitespace char, e.g. space, tab, newline

>>> 'a'.isalpha()
True
>>> 'abc'.isalpha()  # works for multiple chars too
True
>>> 'Z'.isalpha()
True
>>> '$'.isalpha()
False
>>> '@'.isalpha()
False
>>> '9'.isdigit()
True
>>> ' '.isspace()
True

Exercise: alpha_only(s)

> alpha_only

• Given string s
• Return a string of its chars which are alphabetic
  Use the .isalpha() test for each char in s
• e.g. 'H4ip2' returns 'Hip'
• Use the standard for/i/range loop
• If logic inside the loop
  Control if a char is grabbed or not
• This loop pattern generalizes:
  Look at every char in input s
  Build up result string with +=

Solution code

def alpha_only(s):
    result = ''
    
    # Loop over all index numbers
    for i in range(len(s)):
        # Access each s[i]
        if s[i].isalpha():
            result += s[i]
    
    return result

if Variation: if / else

See guide for more if/else details: Python-if

if test-expr:
  Lines-A
else:
  Lines-B

• Regular if - do the body lines, or do nothing
• if/else variant:
  Choose between 2 actions
  Always do one of them
• Run lines-A if test is True
• Run lines-B if test is False
• Style: use if/else to choose 1 of 2 actions
• Only use "else" if it is needed
  Regular "if" solves most problems and is simpler
  Sometimes you "else" to switch between 2 actions
• There is a more rare "elif" option we may cover later

Example: str_dx()

> str_dx

• Return string where every digit changes to 'd'
  And every other char changed to 'x'
• e.g. 'ab42z' returns 'xxddx'
• Use if/else

Solution code

def str_dx(s):
    result = ''
    for i in range(len(s)):
        if s[i].isdigit():
            result += 'd'
        else:
            result += 'x'
    return result

else vs. not

Sometimes beginners sort of back into using else to do something if the test is False, like this:

if some_test:
     pass  # do nothing here
else:
     do_something

The correct way to do that is with not:

if not some_test:
    do_something

Big Picture - Program, Functions, Testing

• Big Picture
• Program Made of many functions

Best Practices

• Divide and Conquer strategy
• Divide program into many functions
• Work on one function at a time
  Deal with each function in isolation
• Test that function
• Write helper functions first, test them
• Later functions can call the helpers after they are tested
• Avoid debugging multiple functions at once
• Today: Python built-in tech for testing a function as you go

str1 project

• Download str1.zip project
• Expand to get "str1" folder
• Open the folder in PyCharm

Python Function - Pydoc

• See digits_only() or str_dx() below
• See triple-quote description at top
• Inside each ">>>" thing within triple quote is a test
• This is known as "Doctest" of the function
  What inputs fn takes
  What it promises to return on the next line
  Black box model
  "Contract" idea

def digits_only(s):
    """
    Given a string s.
    Return a string made of all
    the chars in s which are digits,
    so 'Hi4!x3' returns '43'.
    Use a for/i/range loop.
    (this code is complete)
    >>> digits_only('Hi4!x3')
    '43'
    >>> digits_only('123')
    '123'
    >>> digits_only('')
    ''
    """
    result = ''
    for i in range(len(s)):
        if s[i].isdigit():
            result += s[i]
    return result

Python Function - Doctest

Here are the key lines that make one Doctest:

    >>> digits_only('Hi4!x3')
    '43'

• That syntax spells a test of 1 case
• Looks like a fn call
• Input between the parens
• Output on the next line
• In PyCharm:
  Right click on the test
  Select "Run Doctest ..."
• Output: Process finished with exit code 0
  Also look for "Tests passed" and green checkmark on horizontal bar
  That means it worked perfectly
  This message could be more fun about it the message
• Otherwise get error output
• Experiment: try putting in a bug, run Doctest, fix the bug
• Protip:
  Green "play" button at left re-runs most recent test
  See also top of "Run" menu
  Avoid having to re-click every time

Doctest - Important for Strategy

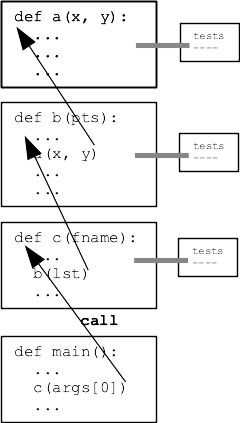
Divide and conquer - want to be able to divide your program up into separate functions, say A, B, and C. Want to work on one function at a time, including testing. Doctests make this really easy - just author the tests right next to where you write the code.

Doctest Workflow

• Starting work on a function
• Write two or three Doctests first, before writing code
• The first test can just be an obvious case, like 'Hi4!x3'
• Add an "edge" case test, like the empty string ''
• Work on the code, run the tests to see where you are
  Debugging with these little tests is relatively easy
  Use green triangle button to re-run easily (control-r may work too)
• Eventually the tests pass and your done!
• Green Checkmark!

We'll use Doctests to drive the examples in section and on homework-3. (Not on the quiz though)

Grid - Peeps Example

Today's grid example peeps.zip

Grid Utility Code

• We have done lots of 2d algorithms on images
  Always with RGB input/output
  Nice, but just one corner of 2d algorithms
• Grid - generic 2d facility
• In the grid.py file
• 2d storage of str, int, .. anything
• Reference: Grid Reference

Grid Functions

• grid = Grid(3, 2) - create, all None initially
• Zero based x,y coordinates for every square in the grid:
  origin at upper left
  x: 0..grid.width - 1
  y: 0..grid.height - 1
• grid.width, grid.height - access width or height
• grid.get(0, 0) - returns contents at x,y (error if out of bounds)
• grid.set(0, 0, 'a') - set at x,y
• grid.in_bounds(2, 2) - return True if x,y is in bounds

Grid Example Code

grid = Grid(3, 2)
grid.width # returns 3
grid.set(2, 0, 'a')
grid.set(2, 1, 'b')

Grid Peeps Problem

Suppose we have a 2-d grid of peeps candy bunnies. A square in the grid is either 'p' if it contains a peep, or is None if empty. We'll say that a peep is "happy" if it has another peep immediately to its left or right.

Peep Happy

Look at the grid squares above. For each x,y .. is that a happy peep x,y?

x, y happy?
(top row)
0, 0 -> False (no peep there)
1, 0 -> True
2, 0 -> True

(2nd row, nobody happy)
0, 1 -> False
1, 1 -> False
2, 1 -> False

Peep Plan

• Build the is_happy(grid, x, y) function
• Write Doctests to check its output
• Need to be able write out a little grid for the testse

Square Bracket Syntax for Grid

Here is the syntax for the above grid. The first [ .. ] is the first row, the second [ .. ] is the second row. This is fine for writing the data of a small grid, which is good enough for writing a test.

grid = Grid.build([[None, 'p', 'p'], ['p', None, 'p']])

Write is_happy() Doctests

def is_happy(grid, x, y):
    """
    Given a grid of peeps and in bounds x,y.
    Return True if there is a peep at that x,y
    and it is happy.
    A peep is happy if there is another peep
    immediately to its left or right.
    >>> grid = Grid.build([[None, 'p', 'p'], ['p', None, 'p']])
    >>> is_happy(grid, 0, 0)
    False
    >>> is_happy(grid, 1, 0)
    True
    >>> is_happy(grid, 2, 0)
    True
    >>> is_happy(grid, 0, 1)
    False
    >>> is_happy(grid, 2, 1)
    False
    """
    pass

Write is_happy() Code

• Use the if/return pick-off strategy
• 1. Pick off the case where x,y is not a peep
• Below (1), know that x,y is a peep
• 2. Look for another peep to the left
  Left is x-1
  Must check that x-1 is in bounds before calling get()
  Without the check, get a "bad list index" error, out of bounds
• 3. Look for another peep to the right .. similar code
• 4. If (2) and (3) did not find anything, return False

is_happy() Code v1

This code is fine. Using the "pick-off strategy, looking for cases to return True. Then return False as the bottom if none of the cases found another peep.

def is_happy(grid, x, y):
    """
    Given a grid of peeps and in bounds x,y.
    Return True if there is a peep at that x,y
    and it is happy.
    A peep is happy if there is another peep
    immediately to its left or right.
    >>> grid = Grid.build([[None, 'p', 'p'], ['p', None, 'p']])
    >>> is_happy(grid, 0, 0)
    False
    >>> is_happy(grid, 1, 0)
    True
    >>> is_happy(grid, 2, 0)
    True
    >>> is_happy(grid, 0, 1)
    False
    >>> is_happy(grid, 2, 1)
    False
    """
    # 1. Check if there's a peep at x,y
    # If not we can return False immediately.
    if grid.get(x, y) != 'p':
        return False

    # 2. Happy because of peep to left?
    # Must check that x-1 is in bounds before calling get()
    if grid.in_bounds(x - 1, y):
        if grid.get(x - 1, y) == 'p':
            return True

    # 3. Similarly, is there a peep to the right?
    if grid.in_bounds(x + 1, y):
        if grid.get(x + 1, y) == 'p':
            return True

    # 4. If we get to here, not a happy peep,
    # so return False
    return False

is_happy() Using and

The in_bounds() checks can be done with and instead nesting 2 ifs. This works because the "and" works through the tests left-to-right, and stops as soon as it gets a False. This code is a little shorter, but both approaches are fine.

    # 2. Happy because of peep to left?
    # here using "and" instead of 2 ifs
    if grid.in_bounds(x - 1, y) and grid.get(x - 1, y) == 'p':
        return True

Doctest Strategy

We're just starting down this path Doctests. Doctests enable writing little tests for each black-box function as you go, which turns out to be big productivity booster. We will play with this in section and on homework-3.