Today - big picture divide and conquer, black box examples, boolean logic, string introduction, string +=, string for/i/range loop -->

Big Picture Strategy - Divide and Conquer

• Q: What is the main technique for solving big problems?
• A: Divide and Conquer
• Divide the big program into functions
• Work on one function at a time
• aka decomposition
• As we build up Python techniques ...
  Many techniques will work in service of this big-picture goal

Work on One Function At a Time
Keep Functions Independent

For Divide-and-Conquer strategy to work, we want to work on one function at a time. To do that, we need the functions to be independent of each other. When working on a function, we're just looking at its code, not having to think about lines from other functions.

We'll work on Python techniques this week, and they will be in service of this one-function-at-a-time strategy.

"Black Box" Function Model - Data Flow

We have this goal of independent functions. How do we think about them so we can fit them together to build the program?

We will characterize each function by its inputs and outputs. This works well for keeping the functions independent, yet having enough information to fit them together.

Black-box model of a function: function runs with its input data, producing the function's output. In Python the input is the functions parameters, and the function's output is from the Python return directive.

Repeatable - Same input, Same Output

Since the function computes using its input data, if called two times with the same inputs, it should produce the same outputs.

Fix Phone Example

Say we are working on an app where people type in phone numbers, like 555-1212.

Suppose that sometimes the user types in a phone number kind of incompetently, with extra spaces and dashes. Imagine a function fix_phone() that takes in the malformed number as an input, and returns a cleaned up phone number as output, with the digits in the right places and one dash.

Think of it as a black box with an input and output, that would look like this:

Cases - Table of Input Output

You could think about fix_phone(), you could think of all the different inputs it should handle, and what the output should be for each one. These leads naturally to thinking about the "Cases" for a function — a table of inputs, and for each input, what should be the output.

In this case, we'll say that if an input number does not have 7 digits, then it is unfixable, and in that case the output should be the special value None, signalling that that input was beyond repair.

Cases - Framework to Think About Function Code

Now we'll starting coding up many black-box input/output functions, starting in the logic 1 section on the experimental server.

The "cases" for each function give us a framework to think about what all different inputs the code needs to handle and what the output should be for each one.

Getting started — thinking about the various cases is a good way to get started with the code for a function. We might use the word systematic to describe the approach, thinking through all the cases to make sure each is handled.

1. winnings1() Example

> winnings1()

• This is a first, simple example, just showing the mechanics
• Say we are writing a function for a lottery game
• Rules: input is an int score 0..10 inclusive
• score 0-4 -> winnings is score * 10
• score 5-10 -> winnings is score * 12
• Can make a table showing output for each input

score -> winnings
0        0
1        10
2        20
3        30
4        40
5        60  # 12x kicks in here
6        72
7        84
8        96
9        108
10       120

1. Function Input: Parameter

def winnings1(score):
    ...

• The parameters to a function are its inputs
  Left side of black-box picture
• e.g. score is the input here
• Code inside the function just uses the parameter value - easy

2. Function Output: return result

def winnings1(score):
    return score * 10

• When a return line runs in a function
• 1. It exits the run of the function immediately
• 2. It specifies the return value that will go back to the caller
  The output or "result" of the function
• So the return statement makes the output of the function right then

Experiment 1 - winnings1()

You can type these in and hit the Run button as we go or just watch as we go. The results are pretty easy to follow.

def winnings1(score):
    return score * 10

• Try 1 line for the function:
  return score * 10
• Look at the table of output
• See the basic roles of parameter/return
• But this output is wrong half the time

Experimental Server Output Format

• Run function on experimental server, generates table of outputs
• It calls the function with many inputs
• Each row shows one input + result
• First "call" column is the input
• Second "got" column is what the function returned
• Easy to see the function's behavior this way
• Black box model: think of function as its inputs and outputs

if-return Pick-Off Strategy

• The function needs to handle all possible input cases
• Have if-logic to detect one case
  Return the answer for that case
  Exiting the function
• Lines below have if-return logic for other cases
• Code is "picking off" the cases one by one
• As we get past if-checks .. input must be a remaining case
• Analogy: coin sorting machine
  Coin rolls past holes, smallest to largest
  1st hole dime, 2nd hole penny, 3rd nickel, 4th quarter
  A dime never makes it to the quarter-hole
  The dime is picked-off earlier

Experiment 2

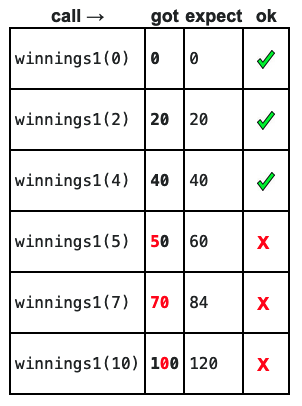
def winnings1(score):
    if score < 5:
        return score * 10

Add if-logic to pick off the < 5 case. Run it. We can see that it's right for half the cases.

None Result

• None is Python's formal value representing nothing
• None is also the default return value of a function
• None is returned if there is no explicit return
• This can happen by "falling off the end" of the function
  All its lines have run and the function is finished
• Above example, we see None if score >= 5
• If you see None like this
  Look at your code: how is the code not doing a return?

Experiment 3 - Very Close

def winnings1(score):
    if score < 5:
        return score * 10

    if score >= 5:
        return score * 12

Add pick-off code for the score >= 5 case (>= means greater-or-equal). This code returns the right result in all cases. There is just at tiny logical flaw.

Experiment 4 - Perfect

def winnings1(score):
    if score < 5:
        return score * 10
    
    # Run gets here: we know score >= 5
    return score * 12

• Each pick-off recognizes a case and exits the function
• Therefore for lines below the pick-off, the picked-off case is excluded
• That is, the score >= 5 test is unnecessary
• This helps with your one-at-a-time attention
  Work on code for case-1
  When that's done, put it out of mind
  Work on case-2, knowing case-1 is out of the picture
• Demo: try < vs. <= Off By One Error
  Good to test both sides of the boundary: inputs 4 and 5

What About This Code?

What about this solution...

def winnings1(score):
    if score < 5:
        return score * 10
        return score * 12

The above does not work. The second return is in the control of the if because of the indentation. It never runs because the line above exits the function. Obviously indentation is very significant for what code means in Python.

Programming - Systematic Cases

• Think through the cases systematically - case-1, then case-2, ...
• This is helpful when you are staring at a blank screen
• Think .. ok, what's one case
  Write if/return to pick-off that one

2. (on your own) Winnings2

Similar practice example on your own.

> winnings2()

Say there are 3 cases. Use a series of if-return to pick them off. Need to think about the order. Need to put the == 10 case early.

Winnings2: The int score number is in the range 0..10 inclusive. Bonus! if score is 10 exactly, winnings is score * 15. If score is between 4 and 9 inclusive, winnings is score * 12. if score is 3 or less, winnings is score * 10. Given int score, compute and return the winnings.

Solution

def winnings2(score):
    if score == 10:
        return score * 15
  
    if score >= 4:  # score <= 9 is implicit
        return score * 12
    
    # All score >= 4 cases have been picked off.
    # so score < 4 here.
    return score * 10

    # Here the cases are handled from 10 to 0.
    # The opposite order would be fine too.

Boolean Values

For more detail, see guide Python Boolean

• "boolean" value in code - True or False
• if-test and while-test work with boolean inputs
• e.g. bit.front_clear() returns a boolean
• So we have if bit.front_clear():

Ways to Get a Boolean

• == operator to compare two things
  2 == 1 + 1 returns True
  Two equal signs
  Since single = is used for var assignment
• != - not-equal test
  2 != 10 returns True
• Compare greater-than / less-than
• < is strict less-than
• <= is less-or-equal
  6 < 10 returns True
6 < 6 returns False (strict)
  6 <= 6 returns True
• > is strict greater-than
• >= is greater-or-equal
• These all work with ints, floats, other types of data

Can try these in the interpreter (Interpreter)

>>> n = 5   # assign to n to start
>>> n == 6
False
>>> n == 5
True
>>> n != 6
True
>>> 
>>> n < 10
True
>>> n < 5  # < is strict
False
>>> 
>>> n <= 5  # less-or-equal
True
>>> 
>>> n > 0
True

Boolean Operators: and or not

• An operator combines values in an expression
  e.g. + operator, 1 + 2 returns 3
• Boolean operators combine True False values
• Boolean operators: and or not
• Suppose here that b1 and b2 are boolean values
• b1 and b2 - if both sides are True, then it is True
  aka all the inputs must be True
• b1 or b2 - if either side or both sides are True, it is True
  aka some input must be True
• not b1 = inverts True/False
  Why does not go to the left?
  It's like the - for a negative number
  e.g. -6

Weather Examples - and or not

Say we have temp variable is a temperature, and is_raining is a Boolean indicating if it's raining or not. Here are some examples to demonstrate and or not:

# have: int temp, boolean is_raining
# OR:  one or the other or both are true
# AND: both must be true

# Say we don't want to go outside if
# if it's cold or raining...

if temp < 50 or is_raining:
    print('not going outside!')

# Say we do want to go outside if
# it's snowing...

if temp < 32 and is_raining:
    print('yay snow!')

Boolean Exercise - Springtime!

What is the code to detect if the temp is over 70 and it's not raining?

if -what goes here?-:
    print('Sunny and nice!')

if temp > 70 and not is_raining:
    print('Sunny and nice!')

Style Note: no == True

In an if or while test, do not add == True or == False to the test - though the English phrasing of it does tend to include those words.

Do it like this:

if is_raining:           # YES like this
    print('raining')

Not like this:

if is_raining == True:   # NO not like this
    print('raining')

The if/while checks if the test is True or False on its own.

Numeric and Example

Suppose we have this code, and n holds an int value.

if n > 0 and n < 10:
   # get here if test is True

What must n be inside the if-statement? Try values like 0 1 2 3 . 8 9 10

You can work out that n must be a an int value in the range 1..9 inclusive.

(optional) 3. is_teen(n) Example

> is_teen()

is_teen(n): Given an int n which is 0 or more. Return True if n is a "teenager", in the range 13..19 inclusive. Otherwise return False. Write a boolean test to pick off the teenager case.

Solution

def is_teen(n):
    # Use and to check
    if n >= 13 and n <= 19:
        return True

    return False

    # Future topic: possible to write this
    # as one-liner: return n >= 13 and n <= 19

4. (optional) Lottery Scratcher Example

> scratcher()

A similar example for practice.

Lottery scratcher game: We have three icons called a, b, and c. Each is an int in the range 0..10 inclusive. If all three are the same, winnings is 100. Otherwise if 2 are the same, winnings is 50. Otherwise winnings is 0. Given a, b and c inputs, compute and return the winnings. Use and/or/== to make the tests.

Solution:

def scratcher(a, b, c):
    # 1. All 3 the same
    if a == b and b == c:
        return 100
    
    # 2. Pair the same (3 same picked off above)
    if a == b or b == c or a == c:
        return 50
    
    # 3. Run gets to here, nothing matched
    return 0

Strings

For more detail, see guide Python Strings

• A very widely used data type
• e.g. a string: 'Hello'
• String is a sequence of "characters" or "chars"
• e.g. urls, paragraphs
• A string written in code is called a "literal"
• e.g. 'This is a string'
• Python string literals written on one line with single quotes ' (prefer)
• Double quote also works " - two ways of writing the same string:
  'Hello'
"Hello"

len() function

• Returns number of chars in string
• Works on other collections too
• Not noun.verb style

>>> len('Hello')
5
>>> s = 'Hello'   # Equivalently
>>> len(s)
5
>>> len('x')
1
>>> len('')
0

Empty String ''

• The "empty string" is the string of 0 chars
• Written like: '' or ""
• This is a valid string, its len is 0
• A common edge case to think about with string algorithms
• Does the code need to work on the empty string?
• Probably yes

Zero Based Indexing - Super Common

• Characters in strings are indexed starting with 0 for the first char
  Index numbers are: 0, 1, 2 .... (length-1)
• Everything in computers uses this zero-based indexing scheme
• Pixels within an image used this, x/y vs. width/height
• Index number addresses each char in the string
• Foreshadow: we'll use index numbers, [ ], and len()...
  For many many linear type data arrangements
  But for today strings

String Square Bracket Index

• Use square bracket to access a char by index number
• Valid index numbers: 0..len-1
• Get out of bounds error for too large index number

>>> s = 'Python'
>>> s[0]
'P'
>>> s[1]
'y'
>>> s[4]
'o'
>>> s[5]
'n'
>>> s[6]
IndexError: string index out of range

String Immutable

• A string in memory is not editable
• "Immutable" is the official word for this
• e.g. square bracket cannot change a string

>>> s = 'Python'
>>> s[0]        # read ok
'P'
>>> s[0] = 'X'  # write not ok
TypeError: 'str' object does not support item assignment

String +

• Plus operator + combines 2 strings to make a new, bigger string
  aka "concatenate"
• Uses new memory to hold the result
• Does not change the original strings

>>> a = 'Hello'
>>> b = 'there'
>>> a + b
'Hellothere'
>>> a
'Hello'

1. Set Var With =

We've already used = to set a variable to point to a value. The code below sets s to point to the string 'hello'.

s = 'hello'

2. Change Var With =

What if we use = to set an existing variable to point to a new value? This just changes the variable to point to the latest value, forgetting the previous value. The assignment = could be translated to English as "now points to".

s = 'hello'
# change s to point to 'bye'
s = 'bye'

Useful Pattern: s = s + something

• Use + to add something at the end of a string, yielding a new bigger string
• Use = to assign the new string back to the variable
• e.g. s = s + 'xxx'
• The += operator works here too
• We are constructing a new, bigger string with each step

>>> s = 'hello'
>>> s = s + '!'
>>> # Q: What is s now?

Answer: s is 'hello!' after the two lines. So s = s + xxx is a way of adding something to the right side of a string. The following form does the exactly the same thing using += as a shorthand:

>>> s = 'hello'
>>> s += '!'

String += Strategy

Use a series of += to add on the end.

>>> s = 'hello'
>>> s += '!'
>>> s += '!'
>>> s
'hello!!'

Recall: String Index Numbers

Here is our string, using zero-based index numbers to refer to the individual chars..

>>> s = 'Python'
>>> s[0]
'P'
>>> s[1]
'y'
>>>

How To Loop Over Those Index Numbers?

The length of the string is 6. The index numbers are 0, 1, 2, 3, 4, 5. How to write a loop that generates those numbers? Use the same range(n) we used to generate x values for an image. Length is 6 and want numbers 0, 1, 2, 3, 4, 5 *mdash; range(6) generates those numbers. Or more generally, use: range(len(s)) generates the index numbers for a string.

Standard loop: for i in range(len(s)):

This is the standard, idiomatic loop to go through all the index numbers. It's traditional to use a loop variable with the simple name i with this loop. Inside the loop, use s[i] to access each char of the string.

• The standard loop to go through all the index numbers
• e.g. s = 'Python'
• Length is 6
• Want index numbers 0, 1, 2, 3, 4, 5
• range(n) returns 0, 1, 2, .. n-1
• So use range(6) aka range(len(s))
• for i in range(len(s)):
i will go through: 0, 1, 2, 3, 4, 5
• Use s[i] to access each char in the loop
• Standard to use the variable name i for this loop
• This loop is so common, it's idiomatic
• We'll see another way to do this later

# have string s, loop over its chars
for i in range(len(s)):
    # access s[i] in here

1. double_char() Example

double_char(s): Given string s. Return a new string that has 2 chars for every char in s. So 'Hello' returns 'HHeelllloo'. Use a for/i/range loop.

> double_char

• This function is a good example
  Loop over s
  Look at each char
  Add to result string
• Standard for/i/range loop to look at every char
• Initialize result = '' variable before loop
• Update in loop: result = result + xxxx
• Use s[i] to access each char in loop
• Return result at end
• Could use += shortcut
• Q: does it work on empty string input?

Solution code

def double_char(s):
    result = ''
    for i in range(len(s)):
        result = result + s[i] + s[i]
    return result

Practice: add_exclaim(s)

If we have time, students do one. Look at each char, like double_char().

'xyz' -> '!x!!y!!z!'

> add_exclaim

Also, see the experimental server section string2 for many problems like double_char()

print() In The Loop

Optional - this is a neat feature, not sure if we're doing it today.

The experimental server has a feature to give a little insight about what's going on inside the loop.

Add inside the loop: print(i, s[i])

def double_char(s):
    result = ''
    for i in range(len(s)):
        print(i, s[i])
        result = result + s[i] + s[i]
    return result

This will print one line for each iteration of the loop, showing what i and s[i] are as the loop runs.

Recall that the print() output is separate from the formal return output of the function. In the experimental server, the print output is shown below the function result, looking like this for the 'xyz' input:

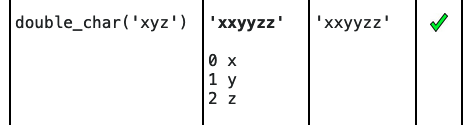
print(i, s[i]) - Think About Output

Say the input is 'xyz'

Q: How many iterations will the loop run?

A: 3 - it runs through the index numbers 0, 1, 2

Q: What lines will print(i, s[i]) produce?

A:

0 x
1 y
2 z