Today: loose ends - comprehension, truthy logic, #! line, float flaws, open source

List Comprehensions

List comprehensions are a beautiful Python feature. For certain problems, they are a short and unbeatable solution. If you are interviewing for an internship, and let slip that you like comprehensions, you will get a knowing nod from the interviewer, like "this kid gets it." (Not needed for any of our homeworks.)

[1, 2, 3, 4] -> [1, 4, 9, 15]

• Like map(), but nicer
• It's fine to use this instead of map()
• Have list of XXX want list of YYY
  e.g. squares [1, 2, 3, 4] -> [1, 4, 9, 16]
• Pattern that appears in code 15% of the time
• Comprehensions are such a beautiful solution for that 15%

Comprehension Syntax 1

• Given a list of elements
• Compute a new list, populated by an expression
  expression: old elem → new elem
• e.g. compute square of each num element

Comprehension 1-2-3

• Nick's mnemonic: re-use syntax of other Python features
• 1. Type in a pair of outer brackets [ ]
• 2. Inside write a foreach for n in nums
  Choose an appropriate var name for the loop, e.g. n or s
• 3. Then the result expression n * n goes on the left
• example: squares, * -1, string uppercase
• example. Make the string form of each number with '!!' after it , like '5!!'
  Type of output does not need to be the same as the input
  Type of output is just whatever expression is on the left

>>> nums = [1, 2, 3, 4, 5, 6]
>>> [n * n for n in nums]
[1, 4, 9, 16, 25, 36]
>>> [n * -1 for n in nums]
[-1, -2, -3, -4, -5, -6]
>>>
>>> strs = ['the', 'donut', 'of', 'destiny']
>>> [s.upper() for s in strs]
['THE', 'DONUT', 'OF', 'DESTINY']
>>> [str(n) + '!!' for n in nums]
['1!!', '2!!', '3!!', '4!!', '5!!', '6!!']

(optional) Try In Interpreter

• Say you have nums = [1, 2, 3, 4, 5, 6]
• 1. Compute num + 10 for each num
• 2. Compute absolute value of n - 3 for each num

>>> nums = [1, 2, 3, 4, 5, 6]
>>> [n + 10 for n in nums]
[11, 12, 13, 14, 15, 16]
>>> [abs(n - 3) for n in nums]
[2, 1, 0, 1, 2, 3]

Comprehension Examples / Exercises

Section on server: Comprehensions

> power2()

> diff21()

> make_upper()

Comprehension + If

• Can add "if" filter on the right hand side
  add at right: if n > 3
  Mnemonic: re-use syntax again
• Left hand side can be just n to pass value through unchanged

>>> nums = [1, 2, 3, 4, 5, 6]
>>> [n for n in nums if n > 3]
[4, 5, 6]
>>> [n * n for n in nums if n > 3]
[16, 25, 36]

(optional) Comprehension-If Exercises

These are all 1-liner solutions with comprehensions.

Syntax reminder - e.g. make a list of nums doubled where n > 3

[2 * n for n in nums if n > 3]

> even_ten (has if)

> up_only (has if)

Comprehensions Replace map()

Comprehensions are easier to write than map(), so you can use them instead. Why did we learn map() then? Because map() is the ideal way to see how lambda works. At this point, you can use comprehensions instead of map, (and exam problems will give full credit to either form, your choice).

Avoid Comprehension Mania - 1 Line Is Ideal

Programmers can get into Comprehension Fever - trying to write your whole program as nested comprehensions. Or it may be a spirit of one-upmanship, like shrinking down the code more than everyone else. However, using comprehensions for everything is a mistake. Comprehensions are so dense, they can be unreadable if too long. Probably 1-line is the sweet spot for a comprehension.

Using regular functions, loops, variables etc. for longer phrases is fine.

Explain Glossed Over Python Lines - see
wordcount.py / pylibs.py

There are lines of Python code we have glossed over. Today we will explain these.

Usual practice: to create a new Python file, copy an existing Python file you have laying around. In this way, you get the #!/usr/bin... and other bits of rote syntax mentioned here.

What is up with that very first line: #!..

#!/usr/bin/env python3

"""
Stanford CS106A Pylibs Example
...

1. #!/usr/bin/env python3

• #!/usr/bin/env python3
• This should be the very first line of your python file
• This indicates that this file contains python-3 code
• Not a requirement, but a good practice
• Unix is an old and super influential operating system
• This is an ancient Unix "shebang" syntax for specifying the type of a file
  For more detail see: Shebang-line
• Most modern Operating Systems include some Unix heritage: Mac OS, Linux, iOS, Android
  Windows is the exception
  But windows software can still use that line

1. #!/usr/bin/python - python2

This is an older form of the first line.

This first line specifies that the file is Python 2 code

#!/usr/bin/python

import sys
...

There are not huge differences between Python version-2 and version-3. You could easily write Python-2 code if you needed to, but Python-3 is strongly preferred for all new work.

Legacy code - that said, many orgs may have old "legacy" python-2 programs laying around, and it's easiest if they just use them and don't update or edit them. The first line #!/usr/bin/env python3 is a de-facto way of marking which version the file is for.

3. End With Boilerplate If-Statement

You do not need to remember all those details. Just remember this: have that if-statement at the bottom of your file as a couple boilerplate lines. It calls the main() function when this file is run on the command line.

...
... python file ..
...

if __name__ == '__main__':
    main()

Run foo.py From Command Line

When you run a program from the command line like this, Python loads the whole file, and then finally calls its main() function.

$ python3 pylibs.py

The if-statement shown above is the bit of code that calls main(). It's a historical quirk that Python does not simply call main() automatically, but it doesn't, so we have this if-statement at the bottom of the file.

Typically, when starting a new Python project, you copy a Python file you have laying around. In this way, you get the boilerplate #!/usr/bin.. line at the start, and this if-main line at the end of the file.

(optional) Why Do We Need This If-statement?

Consider a Run of the Program

Say you run a program like this:

$ python3 wordcount.py poem.txt

In that case, the if __main__ expression will be True. What does it do? It calls the main() function. So if the python file is run from the command line, call its main() function. That is the behavior we want, and it is what the above "if" does.

What Is The Other Way To Load?

What is the other way to load a python file? There is some other python code, and that code imports the python file.

# In some other Python file
# and it imports wordcount
...
import wordcount

In this more unusual case, the above "if" will be False. Loading a python file (module) does not run its main(). So the if-statement runs main() when the python file is itself run from the command line, but does not run main() when the file is imported by another file.

Two Math Systems, "int" and "float" (Recall)

• Two Systems
• int and float are two different worlds
• "float" .. floating decimal point, moves around
• Float and int - each have their own area on the chip
• Look similar, but distinct
• 6 - the int six
• 6.0 - the float six

# int
3  100  -2

# float, has a "."
3.14  -26.2  6.022e23

Math Works, but (clickbat):
Float Has This One Crazy Flaw

• Math works: + - * / min() max() for both int and float fine:
• i.e. mostly don't have to think about it
• Need to use int for indexing - [ ], grid.get(x, y)
• Foreshadow:
  Float mostly works easily
  BUT Float has one crazy flaw .. revealed below

Abstract Math vs. Applied Arithmetic

Crazy Flaw Demo - Adding 1/10th

Note: do not panic! We can work with this. But it is shocking.

What is happening here?

• Garbage digits are almost always part of a float value
• Printing omits a few stored digits at right
• So often do not see the garbage
• But eventually the garbage gets big enough to print...

>>> 0.1
0.1
>>> 0.1 + 0.1
0.2
>>> 0.1 + 0.1 + 0.1    # this is why we can't have nice things
0.30000000000000004
>>> 
>>> 0.1 + 0.1 + 0.1 + 0.1
0.4
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.5
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.6
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.7
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.7999999999999999     # here the garbage is negative
>>> 7 * 0.1
0.7000000000000001

Another example with 3.14

>>> 3.14 * 3
9.42
>>> 3.14 * 4
12.56
>>> 3.14 * 5
15.700000000000001   # d'oh

Float Garbage Digits

• Float arithmetic is a little imprecise, there is a small error
• Off at the 15th digit .. there are erroneous "garbage" digits
• 1. Idea of 1/10th, mathematically pure
• 2. In Python code: looks like this 0.1
• 3. In the computer memory, actually: 0.100000000000013
• There are some garbage digits way off to the right
• The Math Will Not Come Out Exactly Right
• This is a deep feature of float numbers in the computer, applies to all languages
• The print routine hides a few digits, so often the garbage is hidden
  But in the computation, the garbage is there

Conclusion: float math is slightly wrong

Why Must We Have This Garbage?

The short answer, is that with a fixed number of bytes to store a floating point number in memory, there are some unavoidable problems where numbers have these garbage digits off to the right. It is similar to the impossibility of writing the number 1/3 precisely as a decimal number — 0.3333 is close, but falls a little short.

• We think in base 10
• So 0.1 and 2.5 come out "even"
• But 1/3 does not come out even
• Try to write 1/3 out as a decimal number
  Say stop at 10 digits: 0.3333333333
  This 10 digit number differs from 1/3 by a tiny "error" amount
• Some fractions come out even in base 10, and some don't
• The computer uses base 2 internally - 0's and 1's
• In base 2, a different set of numbers don't come out even
  0.1 does not come out even in base 2
• The garbage digits off to the right are due to the tiny error

Crazy, But Not Actually A Problem

• Everyone needs to remember:
• float numbers are generally a little bit wrong
• (int arithmetic, comes out perfect)
• The error is typically far less than 1-trillionth part
• But the error is not zero
• Most computations can handle an error of 1-trillionth part
• So not much of a problem in practice
• e.g. software to decelerate spacecraft as distance to surface decreases
  We can tolerate an error less than 1 trillionth in the distance to the surface
• Indeed, how many digits of accuracy does the input have, maybe 6 digits?

Must Avoid One Thing: no ==

• There is one concrete coding rule
• Do not use == with float
• Exception: 0.0 is reliable for ==
• Any float value * 0.0 will be exactly 0.0

>>> a = 3.14 * 5
>>> b = 3.14 * 6 - 3.14
>>> a == b   # Observe == not working right
False
>>> b
15.7
>>> a
15.700000000000001

How To Compare Floats

• Compare float values
• Do not use ==
• Instead use builtin function math.isclose()
• Or look at abs(a - b)
abs(x) - the absolute value function
  Check if absolute value of difference is very small

>>> a = 3.14 * 5
>>> b = 3.14 * 6 - 3.14
>>>
>>> import math
>>> math.isclose(a, b)
True
>>>
>>> abs(a - b) < 0.0001
True
>>>

int Arithmetic is Exact

• int arithmetic does not have the error problem of float
• int results are exactly correct and repeatable, matching abstract mathematics
• Except overflow - many languages, have a maximum possible int
  Int arithmetic that goes over the max will get the wrong answer - aka "overflow"
  Uniquely, Python does not have a max int

>>> # Int arithmetic is exact
>>> # The two expressions are exactly equal, "precise"
>>> 2 + 3
5
>>> 1 + 1 + 3
5
>>> 
>>> 2 + 3 == 1 + 1 + 3
True
>>>

Doesn't seem like such a high bar .. and yet float does not give us this!

int Bank Balance

Bank balance example: Float is not a good choice for bank balances. Customers do not want to see math a little bit off. Bank balances can be stored as int number of pennies. That way, adding and subtracting from one account to another comes out exactly right and balanced.

# balance is $ 457.12
# store as int pennies
bal = 45712

# withdraw $10, i.e. 1000 pennies
bal -= 1000

# balance is exactly right
bal == 44712

# when printing, put in the '.'
'447.12'

int Bitcoin

In fact, Bitcoin wallets use exactly this int strategy - the amount of bitcoin in a wallet is measured in "satoshis". One satoshi is one 100-millionth of 1 bitcoin. Each balance is tracked as an int number of satoshis, e.g. an account with 0.25 Bitcoins actually has 25,000,000 satoshis. Using ints in this way, the addition and subtraction to move bitcoin (satoshis) from one account to another comes out exactly correct. int is precise!

# bitcoin wallet containing 0.25
# actually int 25,000,000 satoshis
bal = 25000000

# spend 0.1 bitcoin, int 10,000,000
bal -= 10000000

# balance comes out exactly right
bal == 15000000

Optional - if we have time.

Open Source - Python is an Example

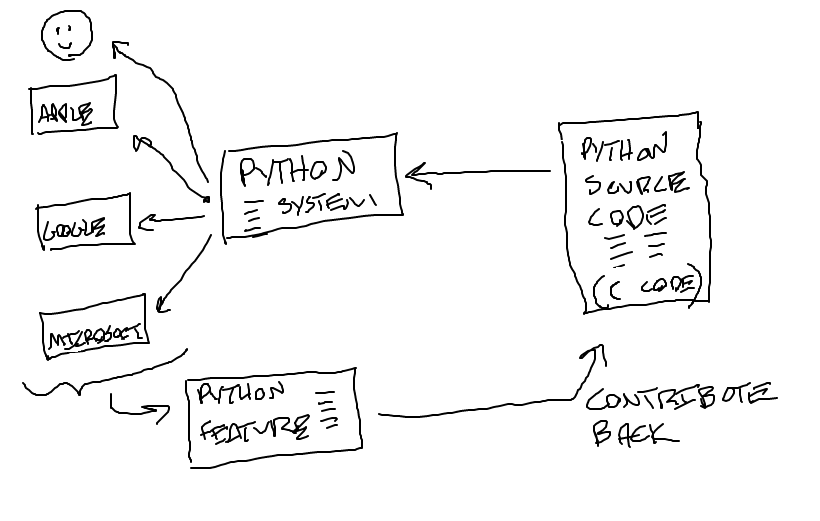
You have noticed that Python works well on your machine, and yet it's free. How does that work? Python is a great example of "open source" software.

Much of the internet is based on open standards - TCP/IP, HTML, JPEG - and open source software: Python (language), Linux (operating system), R (statistics system).

How Open Source Works:

Let's look at Python

Open Source License - Contributions

• Python is distributed for free
• The "source code" of Python is the code to produce Python itself
  Python itself is written in the computer language "C" (CS107)
• Python has an "open source" license
  The source code of Python is distributed liberally
  The license encourages contributing improvements back to Python source code to benefit everyone
• There are many variations in open source licenses, but free and "contribute-back" are the keys

Open Source Economics

• This is an incredibly successful model
• Anyone can build their work on Python, free, not dependent on one vendor
  e.g. Build on Microsoft Visual Basic
  Microsoft charged for it
  And eventually they discontinued it
  Building your expensive technology depending on one vendor looks bad!
• Google, Microsoft, and Apple .. all compete with each other
• But they all use Python
• All contribute to it
• Open source: common infrastructure, we'll all use, nobody's competitive advantage
• A sort of De-Militarized Zone - DMZ
  Apple, Google etc: You can use it for free, if I can use it for free
• Advantage: notice lack of duplication of effort
  Apple, Microsoft, Google .. all using the same infrastructure code!
  This creates some value, not duplicating effort
• Obviously in other domains they have their own tech and compete