Stanford, Fall 2025-26
# CS106A Exam Reference Reminder
# [square brackets] denote functions listed here that we have not used yet
# Exam questions will not depend on functions we have not used yet
Bit:
bit = Bit(filename)
bit.front_clear() bit.left_clear() bit.right_clear()
bit.get_color()
bit.move() bit.left() bit.right()
bit.paint('red') [bit.erase()]
General functions:
len() int() str() range() [list() sorted()]
String functions:
isalpha() isdigit() isspace() isupper() islower()
find() upper() lower() strip()
List functions:
append() index() [extend() pop() insert()]
SimpleImage:
# read filename
image = SimpleImage(filename)
# create blank image
image = SimpleImage.blank(width, height)
# foreach loop
for pixel in image:
# range/y/x loop
for y in range(image.height):
for x in range(image.width):
pixel = image.get_pixel(x, y)
Grid 2D:
grid = Grid.build([['row', '0'], ['row', '1']])
grid.width, grid.height - properties
grid.in_bounds(x, y) - True if in bounds
grid.get(x, y) - returns contents at that x,y, or None if empty
grid.set(x, y, value) - sets new value into grid at x,y
a. Write what value comes from the Python expression:
>>> 2 + 2 * 5 - 3
>>> 104 % 5
>>> 10 ** 2
>>> s = 'Python' >>> s[2:4]
b. What 3 numbers print when the caller() function runs? This code runs without error.
def foo(a, b):
a += 1
b *= 2
return a + b
def caller():
a = 2
b = 3
c = foo(b, a)
print(a, b, c)
# What 3 numbers print?
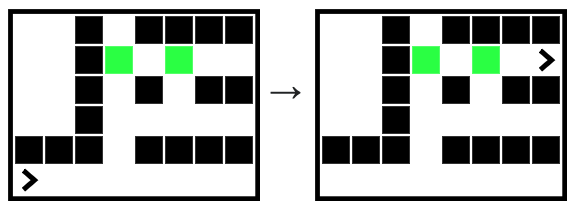
Bit is in a 1-high tunnel, facing the right side of the world. Move bit forward until an opening appears above, the entrance to a vertical hole. Move bit upwards, towards the top of the world until encountering a painted square, i.e. a non-blank square. This marks the entrance to a second tunnel towards the right side of the world. Move bit along this tunnel until blocked. Use three loops.

def loop3(filename):
bit = Bit(filename)
# Your code here
Given an image filename and ints a, b, and c which are 1 or more.
Produce a new out image with three features: (1) A blank vertical rectangle a pixels wide at the left edge of the output, with an aqua rectangle b pixels wide immediately to its right. (2) To the right of the rectangles, a horizontally flipped copy of the original image. (3) Above and below the image, blank rectangles c pixels high and the same width as the image.
1. Write one line of code to create the out image.
2. Almost all of the code to write the flipped image is provided — looping over the original image, writing the colors at each "pixel" to "pixel_out". Write the one line of code which sets the "pixel_out" variable used by the later lines in this loop. It's fine to write the parameters on multiple lines to make them fit. Please avoid writing too near the paper edge, as this makes it hard on the graders.
3. Write the loops and other needed code to produce the aqua rectangle. These are separate loops, not nested inside the earlier loops. To set each white pixel to aqua, the last line in the loop is like pixel_out.red = 0. We'll assume there is a return out as the last line.
def do_image(filename, a, b, c):
image = SimpleImage(filename)
#### 1. Create "out" image
# Write flipped image to out
for y in range(image.height):
for x in range(image.width):
pixel = image.get_pixel(x, y)
#### 2. Set "pixel_out"
pixel_out.red = pixel.red
pixel_out.green = pixel.green
pixel_out.blue = pixel.blue
#### 3. Fill aqua rectangle
a. Given a string s. If the first and last chars of the string are both alphabetic, then return a string length 2 made of those 2 chars. For example 'Py67on' returns 'Pn'. Otherwise return the empty string.
alpha2('a$cd') -> 'ad'
alpha2('abc$') -> ''
alpha2('x') -> 'xx'
alpha2('') -> ''
def alpha2(s):
b. This function has two parameters — s is a string, and add_parens is a boolean, either True or False. Return a new string made of the alphabetic chars in s. If add_parens is True, surround each added char with parenthesis like '(a)', and otherwise add the char just by itself 'a'. Solve using the loop of your choice.
parens('Ab5by$', True) -> '(A)(b)(b)(y)'
parens('Ab5by$', False) -> 'Abby'
def parens(s, add_parens):
c. Given a string s.
There are two ways to return a number from the string.
(1) If there is an '@' char, and the char immediately after it is a digit,
then return the value of that digit + 1.
If the '@' does not work, we have (2): if there is an '!',
and it is not the first char in s, then the whole substring of s before the '!'
is guaranteed to be a number. Return the value of that number + 1.
If the '!' does not work, return -1.
adder('123@59x') -> 6
adder('123@x') -> -1
adder('123!59@') -> 124
adder('!xyz') -> -1
def adder(s):
d. Given a "chars" list containing individual chars, e.g. ['7', 'b', 'o'].
Construct and return a new list containing the chars
from the chars list which are alphabetic, except do not add a char to the result if that char is already in the result. Therefore, there will be no duplicate chars in the result. Solve with a loop.
alpha_x(['7', 'b', 'o', 'o', 't', '$', 'b', 's']) ->
['b', 'o', 't', 's']
def alpha_x(chars):
e. Given a string s. We'll call a '^^^' substring in s a "hats". Find the first hats in s, and then find a second, non-overlapping hats that comes after the first. If there are not two hats, then return the empty string. Otherwise, if both hats exist, then consider the substring between the hats, and the substring after the second hats. If the between substring is the longer of the two, choose the between substring for the last step. Otherwise, choose the after substring. For the last step, call the alpha2(s) function from part (a), passing in the chosen substring, and return the value alpha2(s) returns. For this problem, we assume that alpha2(s) works correctly. Use s.find() and slices.
'x^^^abc^^^xy' -> choose 'abc' -> 'ac' 'x^^^ab^^^xy' -> choose 'xy' -> 'xy' 'xyz' -> '' def hats(s):
In this problem, every square is one of these three values: empty None, bear 'b', honey 'h'. As usual, you can get full credit for each part independently of what you write on the other parts.
Write code for rotate(grid, x, y, down, left)x, y which are in-bounds, and down, left which are int values, 1 or greater. The square down squares straight below x, y, we'll call the "down" square. The square down squares below and left squares to the left of x, y we'll call the "down-left" square. There are three conditions for the rotation to happen:
1. There must be a bear at x, y.
2. The down square must be empty.
3. The down-left square must be non-empty (i.e. it could contain a honey or a bear)
If the 3 conditions are met, the function should move the contents of the down-left square to the down square, and move the bear at x, y to the down-left square, making its original square empty. If the conditions are not met, return the grid unchanged. If you need to write a long line of code, you can write "..." at the end of a line and continue writing on the next line.
def rotate(grid, x, y, down, left):
(b) Add the two lines to complete the following Doctest for a call to rotate() where the action succeeds and the bear moves. The first Grid.build() line is provided, building a small grid suitable for this Doctest.
>>> grid = Grid.build([['b', 'b', 'b'], [None, 'h', None]]) >>>
This problem resembles the homework encryption, but with some differences. As a simplification, we will not handle uppercase input chars. The source and slug lists contain lowercase chars as usual, except there is a single '@' in the slug list, and it may be at any index. The slug list is 1 longer than the source list because of this extra char.
If the input char is in the source, and its index is before the index of the '@', then the encrypted form is the char at the same index in the slug. Alternately, if the index of the input char is not before the '@' index, then the encrypted form is at the input char index plus 1 in the slug, converted to upper case. If the input char is not in the source, then the encrypted form is the input char unchanged.
Examples using above lists encrypt 'a' -> 'c' encrypt 'e' -> 'B' encrypt '$' -> '$'
def encrypt_char(source, slug, ch):
##### 1. Short Answer
9
4
100
'th' # ok if they omit the quote marks
2 3 8
##### 2. Bit
def tmp(filename):
bit = Bit(filename)
# Move to the vertical hole
while not bit.left_clear():
bit.move()
# Move up to the non-blank
bit.left()
while bit.get_color() == None:
bit.move()
# Move to end of the tunnerl
bit.right()
while bit.front_clear():
bit.move()
##### 3. Image
out = SimpleImage.blank(image.width + a + b, image.height + 2 * c)
pixel_out = out.get_pixel(a + b + image.width - 1 - x, y + c)
# or out.width - 1 - x
for y in range(out.height):
fox x in range(b):
pixel_out = out.get_pixel(a + x, y)
pixel_out.red = 0
##### 4. Strings
def alpha2(s):
# If length is 0, the first/last access don't work
if len(s) == 0:
return ''
if s[0].isalpha() and s[len(s) - 1].isalpha():
return s[0] + s[len(s) - 1]
return ''
def parens(s, add_parens):
result = ''
for ch in s:
if ch.isalpha():
# Either add with parens, or plain
if add_parens:
result += '(' + ch + ')'
else:
result += ch
# or with a series of 3 +=
# if add_parens:
# result += '('
# result += ch
# if add_parens:
# result += ')'
return result
def adder(s):
at = s.find('@')
if at != -1:
if at + 1 < len(s) and s[at + 1].isdigit():
return int(s[at + 1]) + 1
exclaim = s.find('!')
if exclaim != -1 and exclaim > 0:
before = s[:exclaim] # all the text before the !
return int(before) + 1
return -1
def alpha_x(chars):
result = []
for ch in chars:
if ch.isalpha() and ch not in result:
result.append(ch)
return result
def hats(s):
a = s.find('^^^')
b = s.find('^^^', a + 3)
if a == -1 or b == -1:
return ''
# Putting the substrings in vars helps a bit
between = s[a + 3:b] # between the hats
after = s[b + 3:] # after the second hat
if len(between) > len(after):
return alpha2(between)
return alpha2(after)
##### 5. Bear Rotation
def rotate(grid, x, y, down, left):
# x,y must be bear
if grid.get(x, y) != 'b':
return grid
# (here testing the must-be-true series)
# down should be in bounds and empty
if grid.in_bounds(x, y + down) and grid.get(x, y + down) == None:
# down-left should not be empty
if grid.in_bounds(x - left, y + down) and grid.get(x - left, y + down) != None:
# if we get here - move happens
# move thing at down-left to down
# here holding "thing" in a var, or there are
# other ways
thing = grid.get(x - left, y + down)
grid.set(x, y + down, thing)
# move bear
grid.set(x - left, y + down, 'b')
grid.set(x, y, None)
return grid
return grid
# -OR- could detect / return the various ways it can fail.
# # down square should be in bounds and empty
# if not grid.in_bounds(x, y + down):
# return grid
# if grid.get(x, y + down) != None:
# return grid
#
# # down-left should be bounds and not empty
# if not grid.in_bounds(x - left, y + down):
# return grid
# if grid.get(x - left, y + down) == None:
# return grid
##### 6. Encryption
def encrypt3(source, slug, ch):
if ch in source:
# Get the index of the '@' for use in the algo
at = slug.index('@')
idx = source.index(ch)
# 1. Before the at
if idx < at:
return slug[idx]
# 2. After the at, add 1 to index
return slug[idx + 1].upper()
return ch