Trees
CS 106B: Programming Abstractions
Spring 2021, Stanford University Computer Science Department
Lecturer: Chris Gregg, Head CA: Chase Davis

Slide 2
Announcements
- Assignment 5 is due tomorrow (late extension until Sunday), and Assignment 6 is due next Wednesday
- We will post Assignment 6 today. It is a scaled-back assignment, so should be doable by Wednesday
- You should start working on your personal project
- The personal project is your final assessment!
Slide 3
Today's Topics
- Refresh on what pointer diagrams represent
- Quick comment on doubly-linked lists
- Introduction to the tree data structure
- You've already seen lots of tree structures
- Tree terminology
- How do we build trees programatically?
- Writing code to traverse a tree
Slide 4
Pointer Diagram Refresh
- The following diagram was put together by a student last Spring:
- Pointers have values that are memory addresses.
- All variables and objects have their own memory address where they are located
- The
nextpointer is a memory address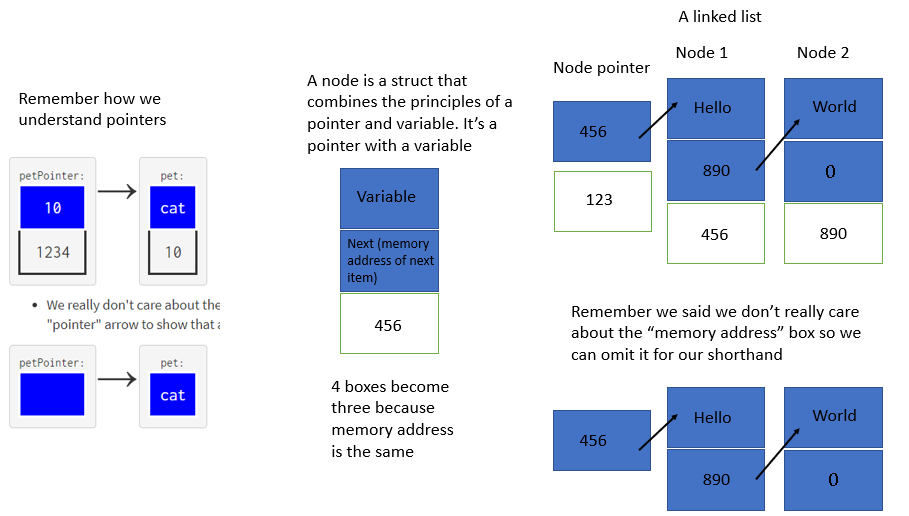
Slide 5
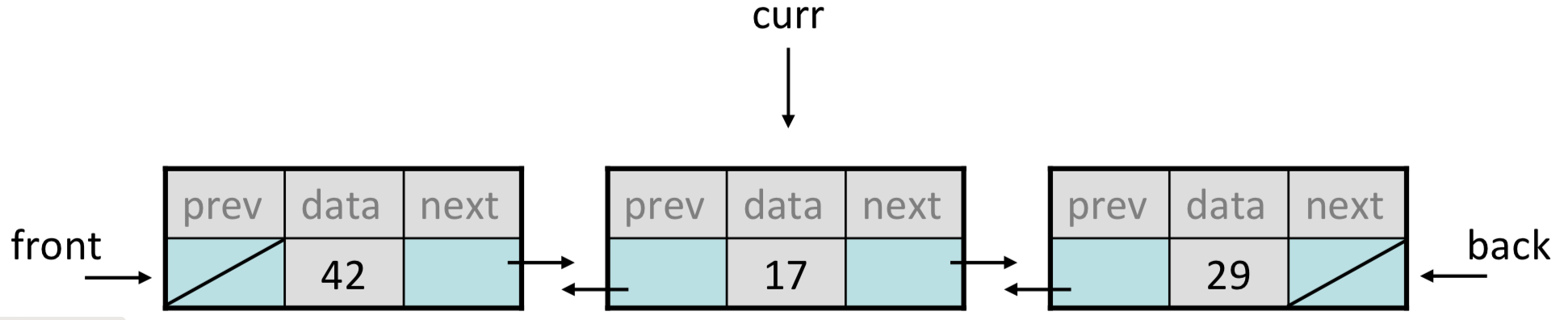
Doubly-linked lists
- Last time, we discussed linked lists. Specifically, we discussed singly linked lists, which have a single
nextpointer in each node, and are strictly one-way. - We also can create a doubly linked list, which has pointers in both directions:
struct ListNode { int data; ListNode* prev; ListNode* next; }; - We will keep a
_frontand a_backpointer in the class, too:class DoublyLinkedList { ... private: ListNode* _front; ListNode* _back; }; -
We can draw the nodes sideways for a bit more intuitive pictures: ```

- We can traverse in either direction with a doubly linked list:
ListNode* curr = _front; // print in forward order while (curr != nullptr) { cout << curr->data; curr = curr->next; } ListNode* curr = _back; while (curr != nullptr) { // print in reverse order cout << curr->data; curr = curr->prev; }
Slide 6
Adding nodes to a doubly linked list
- If we want to add a new node to a doubly-linked list, we don't have to stop on the previous node, and we could find the node in either direction.
- However, we have to change four pointers, which can make coding up a doubly lnked list tricky.
- Let's say we want to add the following
newNodebefore the 17, and we havecurron the 17: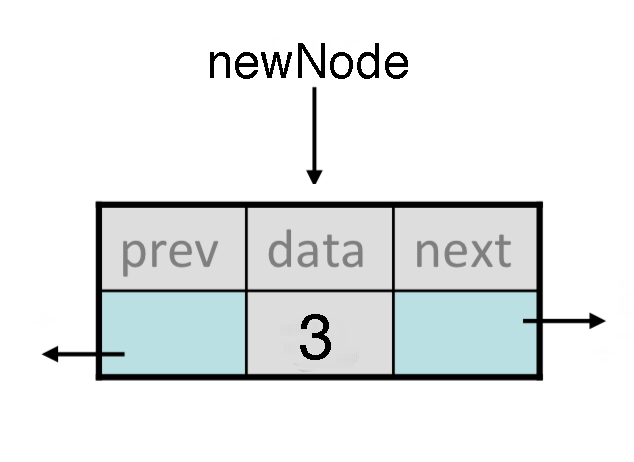
- We would have to change four different pointers. Here's how we would make those changes (and order is important!):
curr->prev->next = newNode; newNode->prev = curr->prev; curr->prev = newNode; newNode->next = curr;Removing nodes from a doubly linked list
- If we want to remove a new node to a doubly-linked list, we don't have to stop on the previous node, and we could find the node in either direction.
- In this case, we only have to make changes to two pointers, the previous node's
next, and the next node'sprev. - Let's say we want to remove the 17 from the list below, and we've stopped
curron that node:
- Here are the changes we have to make:
curr->prev->next = curr->next; curr->next->prev = curr->prev; delete curr;
Slide 7
Trees
- We have seen trees in this class before, in the form of decision trees:
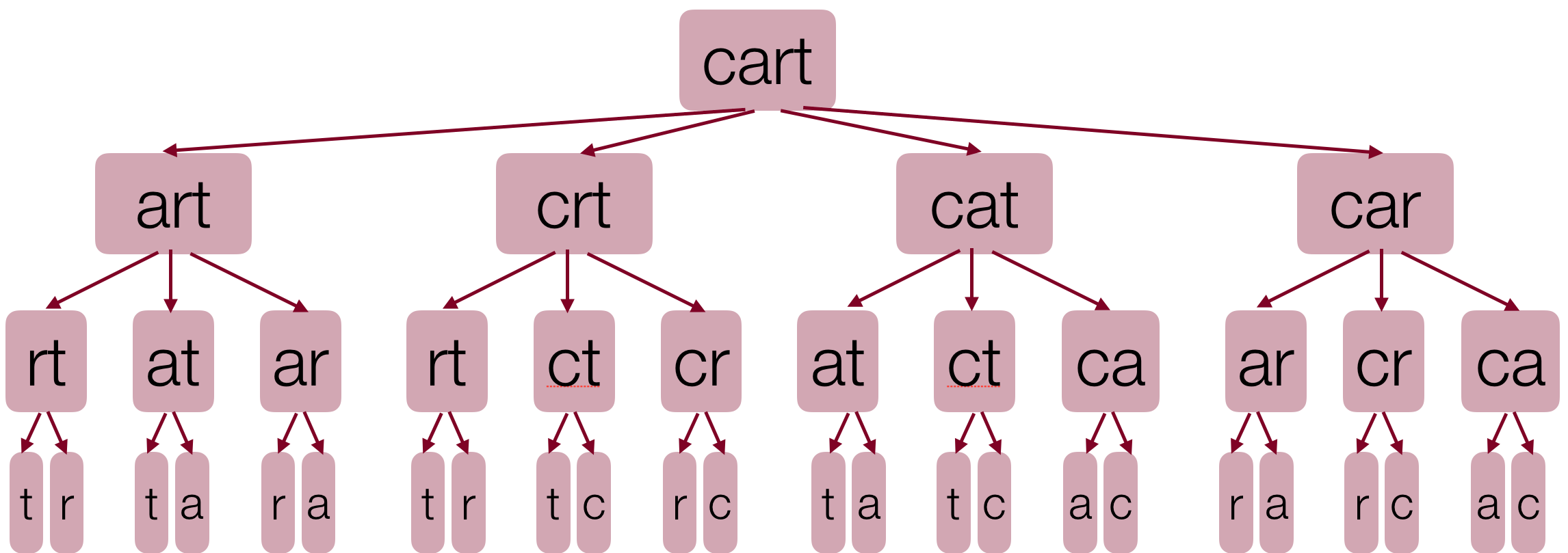
- Trees can describe hirearchies:
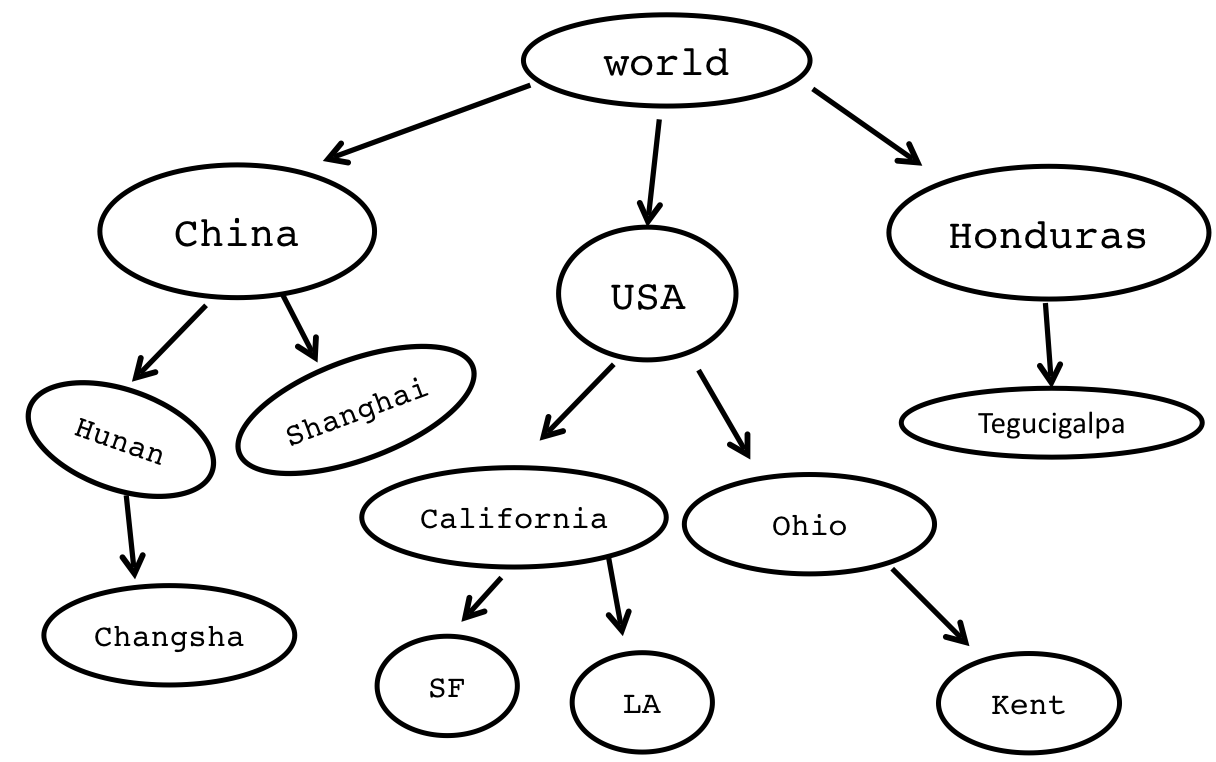
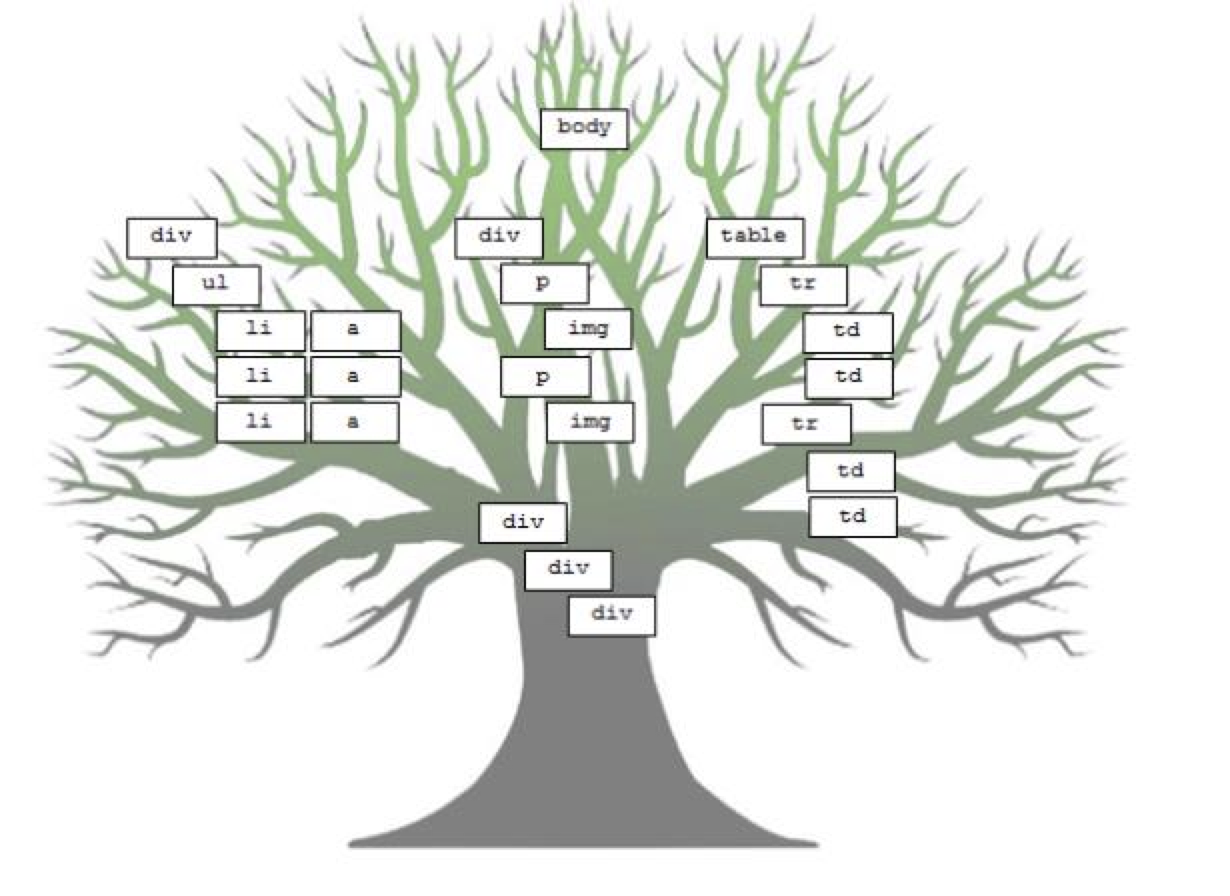
- Trees can describe websites:
- Trees can desceribe programs (we often call them abstract syntax trees (the following is a figure in an academic paper written by a recent CS 106 student!)
// Example student solution function run() { // move then loop move(); // the condition is fixed while (notFinished()) { if (isPathClear()) { move(); } else { turnLeft(); } // redundant move(); } }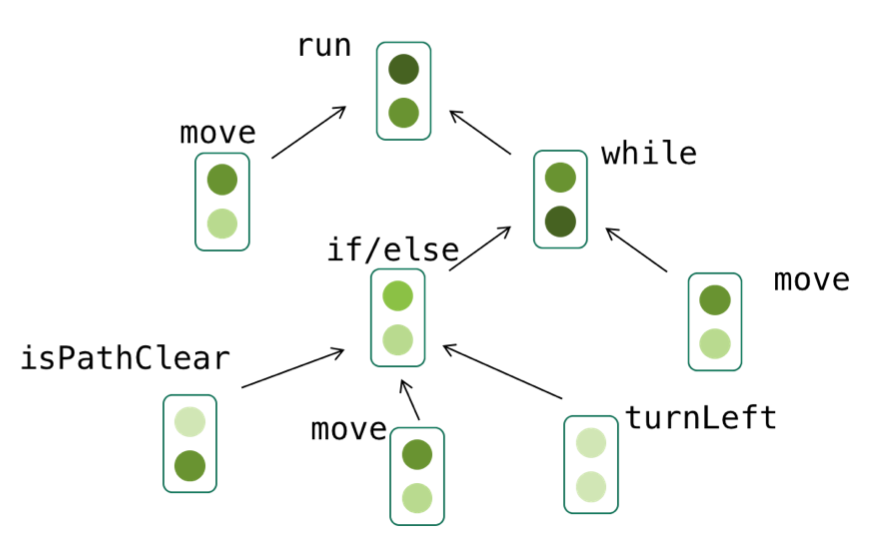
Slide 8
Trees are inherently recursive
- What is a tree in computer science?
- A tree is a collection of nodes, which can be empty. If it is not empty, there is a root node,
r, and zero or more non-empty subtrees,T1,T2, …,Tk, whose roots are connected by a directed edge fromr.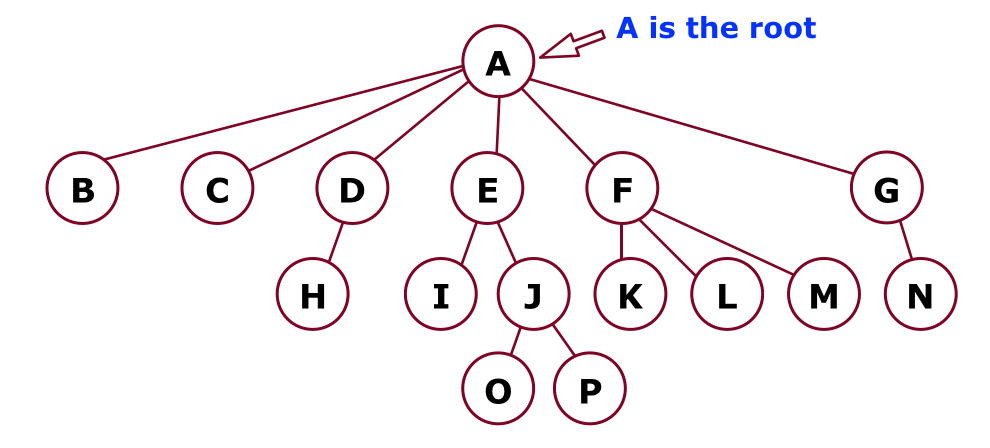
- A tree is a collection of nodes, which can be empty. If it is not empty, there is a root node,
(root)
-----------A--------------
↙︎ ↙︎ ↙︎ ↓ ↘︎ ↘︎
B C D E F-- G
↙︎ ↙︎ ↘︎ ↙︎ ↘︎ ↘︎ ↘︎
H I J K L M N
↙︎ ↘︎
O P
- There are N nodes and N-1 edges in a tree.
- Tree terminology. In the diagram above:
- B is a child of A, and F is a child of A and a parent of K, L, M.
- Nodes with no children are leaves. Nodes B, C, H, I, K, L, M, N, O, and P are all leaves.
- Nodes with the same parent are siblings. I and J are siblings. K, L, and M are siblings. Nodes O and P are siblings. Nodes H and N do not have any siblings (only children).
Slide 9
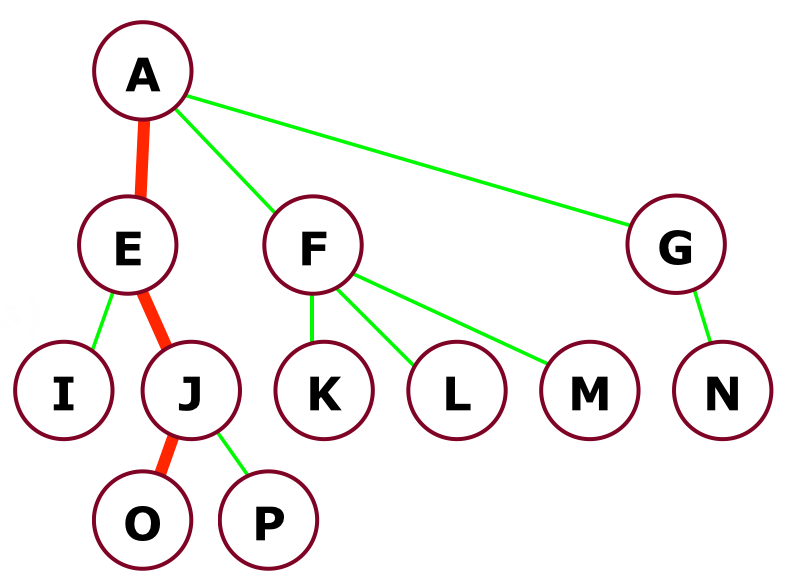
More Tree Terminology
(root)
A--------------
↓ ↘︎ ↘︎
E F G
↙︎ ↘︎ ↙︎ ↘︎ ↘︎ ↘︎
I J K L M N
↙︎ ↘︎
O P
- We can define a path from a parent to its children. The path from A to O is: A-E-J-O.
- The path A-E-J-O has a length of three (the number of edges).
- The depth of a node is the length from the root. The depth of node J is 2. The depth of the root is 0.
- The height of a node is the longest path from the node to a leaf. The height of node F is 1. The height of all leaves is 0.
- The height of a tree is the height of the root. The height of the above tree is 3.
Slide 10
One Parent, No Cycles

- Tree nodes can only have one parent, and they cannot have cycles
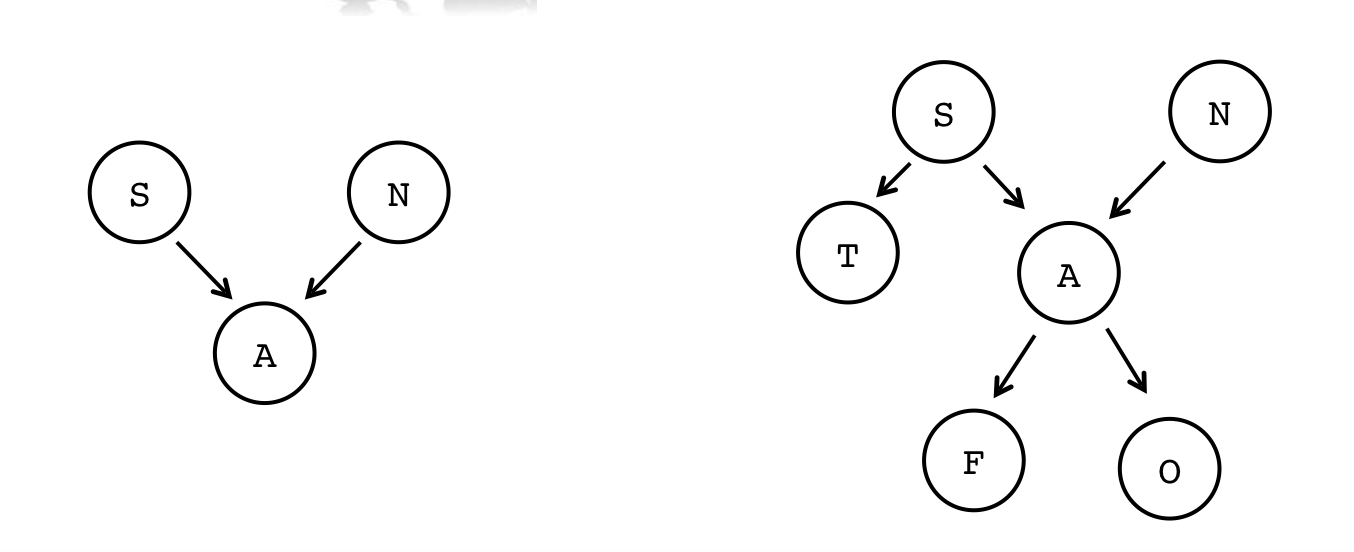
- Not a tree (A has two parents):
S N ↘︎ ↙︎ A - Again: not a tree (A has two parents):
S N ↙︎ ↘︎ ↙︎ T A ↙︎↘︎ F O - The following are not trees, either, because you can cycle through the tree. Nodes cannot have children that are on the same level or above on the tree:
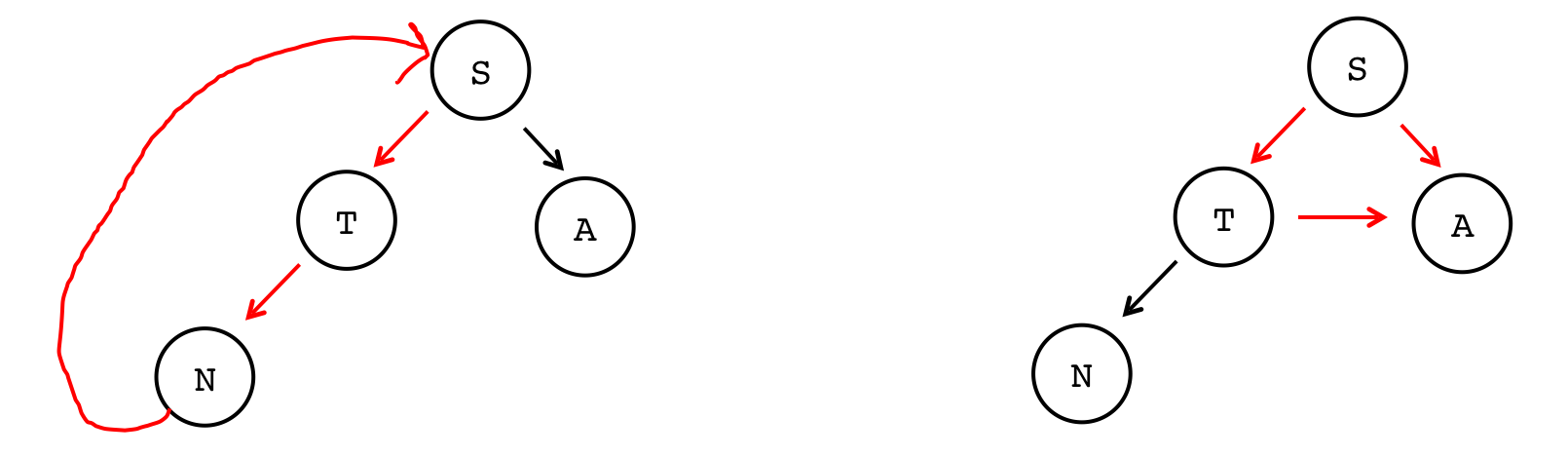
- Not a tree (cycle from N back to S):
→→→→S ↑ ↙︎ ↘︎ ↑ T A ↑↙︎ N - Again: not a tree (the arrow from T to A causes a cycle):
S ↙︎ ↘︎ T→→→A ↙︎ N
Slide 11
Building trees programatically
- To build a tree, we need a new version of our
Node. In this case, we want eachNodeto have a data value (like a linked list), but now we want to pointers, one to the left child, and one to the right child:struct TreeNode { string data; TreeNode* left; TreeNode* right; };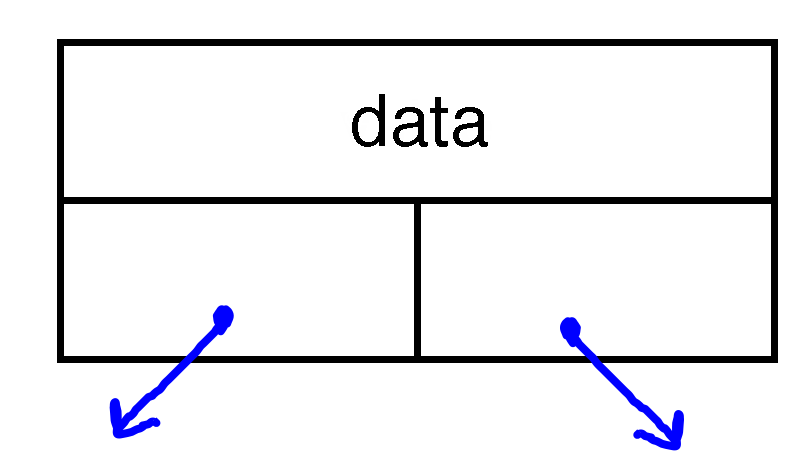
- We don't have to limit ourselves to binary trees, by the way: we could have a ternary tree:
struct TernaryTreeNode { string data; TernaryTreeNode* left; TernaryTreeNode* middle; TernaryTreeNode* right; };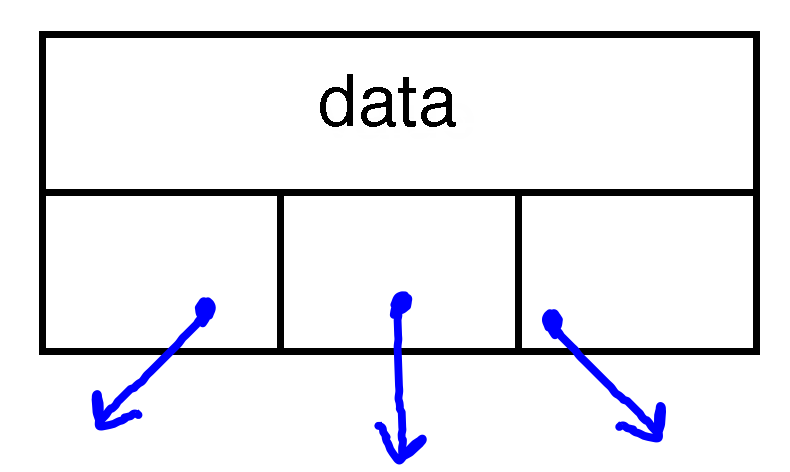
- In fact, we could have any number of children (we may look at the Trie data structure, which can be built this way). This is an N-ary Tree:
struct NAryTreeNode { string data; Vector<NAryTreeNode*> children; };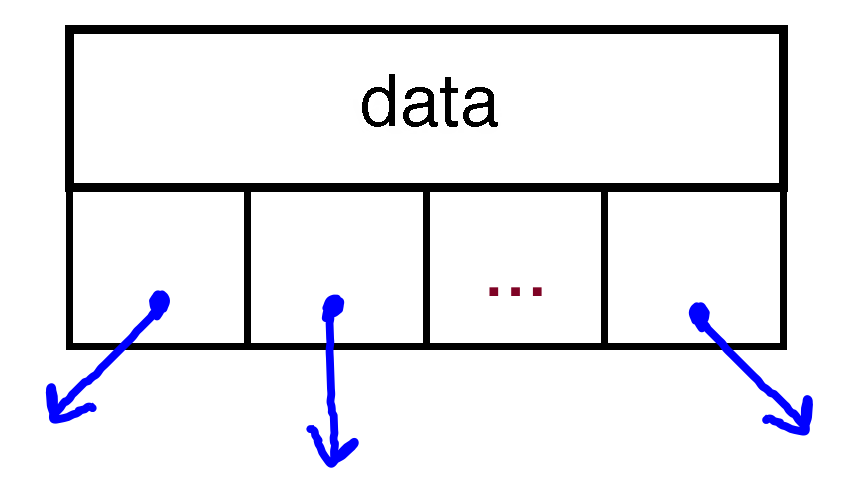
Slide 12
Traversing a Tree
- Often, we will want to do something with each node in a tree. Like linked lists, we can traverse the tree, but it is more involved because of all the branching.
- There are four different ways to traverse a binary tree:
- Pre-order
- In-order
- Post-order
- Level-order
- Let's write some code for each traversal to see the differences. We'll look at two trees:
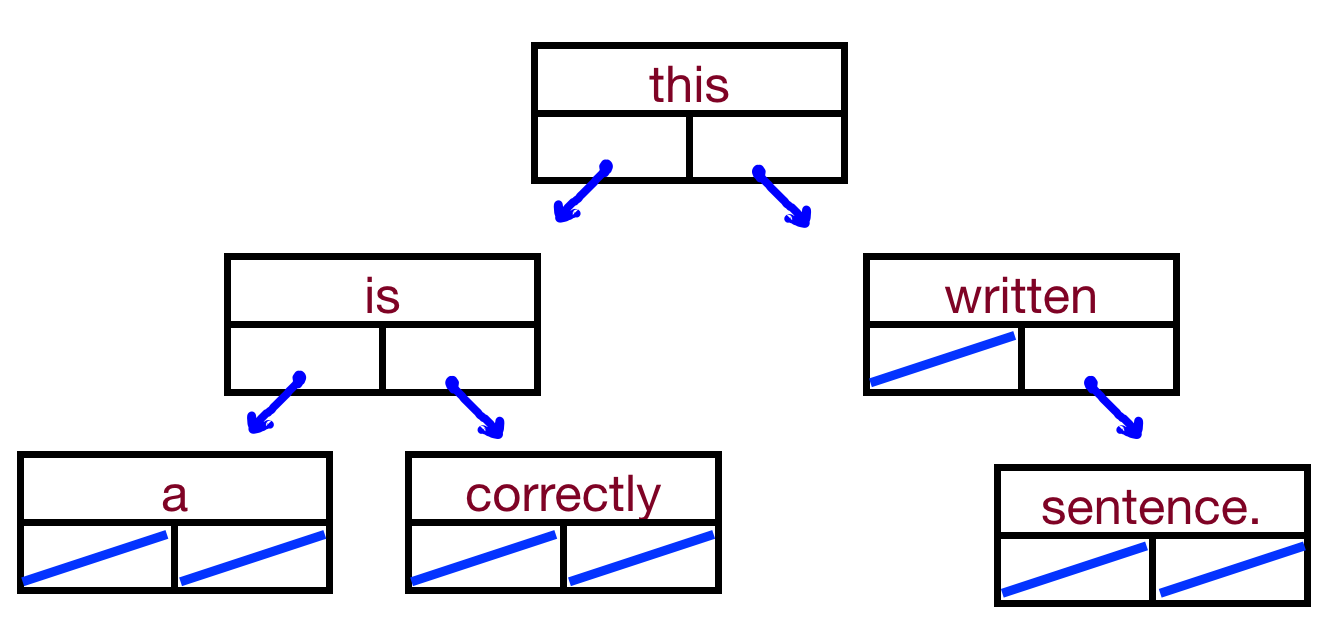
this ↙︎ ↘︎ is written ↙︎ ↘︎ ↘︎ a correctly sentence - We'll also look at:
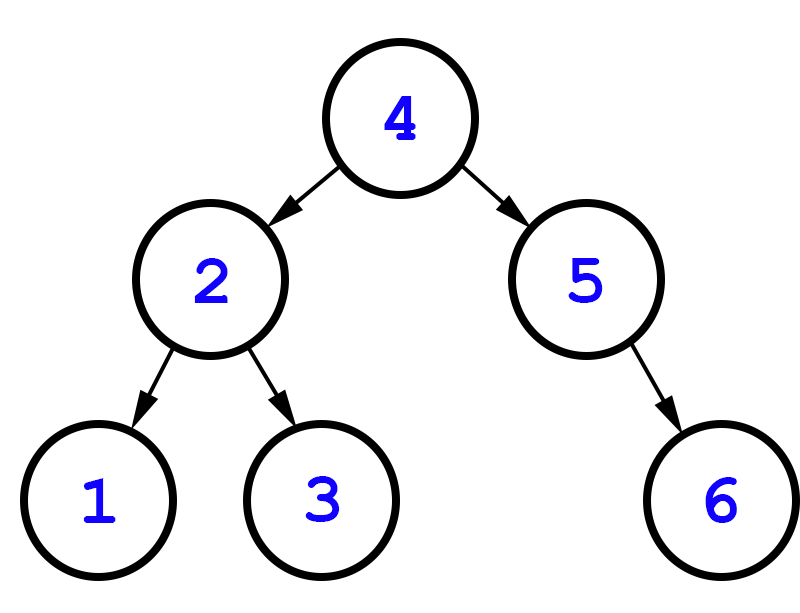
4 ↙︎ ↘︎ 2 5 ↙︎ ↘︎ ↘︎ 1 3 6 - By the way: trees do not have to be complete, like heaps. Any node can have 0, 1, or 2 children.
Slide 13
Pre-order traversal
- The algorithm for a pre-order traversal is as follows:
- Do something
- Go left
- Go right
- This is an inherently recursive algorithm
- For our tests, let's make the "Do something" part print the data at a particular node.
- Code:
void preOrder(TreeNode* tree) { if(tree == nullptr) return; cout<< tree->data <<" "; preOrder(tree->left); preOrder(tree->right); }
Slide 14
In-order traversal
- The algorithm for a in-order traversal is as follows:
- Go left
- Do something
- Go right
- This is also an inherently recursive algorithm
- Code:
void inOrder(TreeNode* tree) { if(tree == nullptr) return; inOrder(tree->left); cout<< tree->data <<" "; inOrder(tree->right); }
Slide 15
Post-order traversal
- The algorithm for a post-order traversal is as follows:
- Go left
- Go right
- Do something
- This is also an inherently recursive algorithm
- Code:
void postOrder(TreeNode* tree) { if(tree == nullptr) return; postOrder(tree->left); postOrder(tree->right); cout<< tree->data <<" "; }
Slide 16
Level-order traversal
- A level order traversal is different than all the others – we want to go one level at a time and print out each node, then go to the next level.
- For this tree, it would be:
this is written a correctly sentence
- Can we do this recursively!
- But, we can use an algorithm you've seen before: breadth first search!
- This is going to use a queue, just like the BFS you did for your maze solving assignment.
- Enqueue the root node
- While the queue is not empty
- dequeue a node
- do something with the node
- enqueue the left child if it exists
- enqueue the right child if it exists
- This is going to use a queue, just like the BFS you did for your maze solving assignment.
- Code:
void levelOrder(TreeNode *tree) { Queue<TreeNode *>treeQueue; treeQueue.enqueue(tree); while (!treeQueue.isEmpty()) { TreeNode *node = treeQueue.dequeue(); cout << node->value << " "; if (node->left != nullptr) { treeQueue.enqueue(node->left); } if (node->right != nullptr) { treeQueue.enqueue(node->right); } } }