Lecture Preview: Spanning Trees and Kruskal's Algorithm
(Suggested book reading: Programming Abstractions in C++, Chapter 18 section 18.6)
Today we will learn about minimum spanning trees in graphs. A spanning tree of a graph is a set of edges that connects all vertices in the graph with no cycles. The following figure shows a graph at left, and a spanning tree of that graph at right:

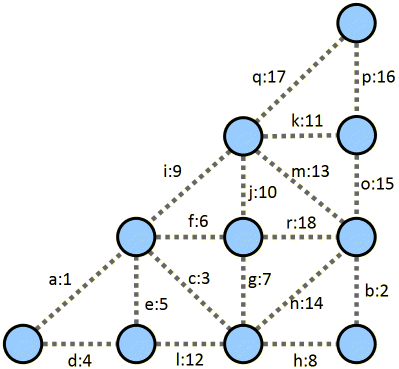
In weighted graphs, we are often interested in finding a minimum spanning tree, which is a spanning tree whose total edge weight is as low as possible. Consider the following weighted graph. A minimum spanning tree on that graph would be {a, b, c, d, f, h, i, k, p}, with a total edge weight of 60.
 →
→
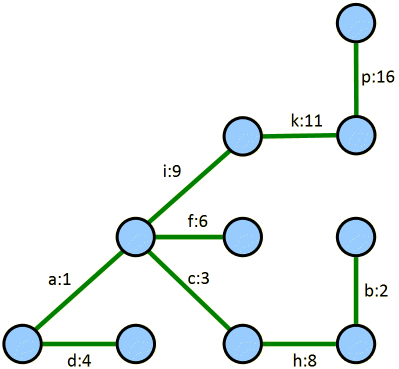
There are several algorithms for finding minimum spanning trees. In lecture we will learn about one called Kruskal's algorithm, which basically just adds edges into the graph in ascending weight order until the graph is connected.
