Friday, January 7, 2022
Computer Systems
Winter 2022
Stanford University
Computer Science Department
Reading: Reader: Bits and Bytes, Textbook: Chapter
2.2
Lecturer: Chris Gregg
CS 107
Lecture 2: Integer
Representations
Today's Topics
•Logistics
•Assign0 —Due Monday
•Labs start Tuesday
•Office hours in full coverage
•Reading: Reader: Bits and Bytes, Textbook: Chapter 2.2 (very mathy…)
•Integer Representations
•Unsigned numbers
•Signed numbers
•two's complement
•Signed vs Unsigned numbers
•Casting in C
•Signed and unsigned comparisons
•The sizeof operator
•Min and Max integer values
•Truncating integers
•two's complement overflow
Information Storage
In C, everything can be thought of as a block of 8 bits
Information Storage
In C, everything can be thought of as a block of 8 bits
called a "byte"
Information Storage
We will discuss manipulating bytes on a bit-by-bit level, but we won't be
able to consider an individual bit on its own.
In a computer, the memory system is simply a large array of bytes (sound
familiar, from CS106B?)
728314 99 -6 3 45 11
200 201 202 203 204 205 206 207 208 209
0xc8 0xc9 0xca 0xcb 0xcc 0xcd 0xce 0xcf 0xd0 0xd1
values (bytes):
address (decimal):
address (hex):
Each address (a pointer!) represents the next byte in memory.
E.g., address 0 is a byte, then address 1 is the next full byte, etc.
Again: you can't address a bit. You must address at the byte level.
Byte Range
Because a byte is made up of 8 bits, we can represent the range of a byte
as follows:
00000000 to 11111111
This range is 0 to 255 in decimal.
But, neither binary nor decimal is particularly convenient to write out bytes
(binary is too long, and decimal isn't numerically friendly for byte
representation)
So, we use "hexadecimal," (base 16).

Hexadecimal
Hexadecimal has 16 digits, so we augment our normal 0-9 digits with six
more digits: A, B, C, D, E, and F.
Figure 2.2 in the textbook shows the hex digits and their binary and
decimal values:

Hexadecimal
•In C, we write a hexadecimal with a starting 0x. So, you will see
numbers such as 0xfa1d37b, which means that it is a hex number.
•You should memorize the binary representations for each hex digit. One
trick is to memorize A (1010), C (1100), and F (1111), and the others
are easy to figure out.
•Let's practice some hex to binary and binary to hex conversions:
Convert: 0x173A4C to binary.
0x173A4C is binary
0b000101110011101001001100

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Hexadecimal
Convert: 0b1111001010110110110011 to hexadecimal.
0b1111001010110110110011
is hexadecimal 3CADB3
(start from the right)

Decimal to Hexadecimal
To convert from decimal to hexadecimal, you need to repeatedly divide
the number in question by 16, and the remainders make up the digits of
the hex number:

Hexidecimal to Decimal
To convert from hexadecimal to decimal, multiply each of the hexadecimal
digits by the appropriate power of 16:

Let the computer do it!
Honestly, hex to decimal and vice versa are easy to let the
computer handle. You can either use a search engine (Google
does this automatically), or you can use a python one-liner:

Let the computer do it!
You can also use Python to convert to and from binary:
(but you should memorize this as it is easy and you will use it
frequently)
Integer Representations
Integer Representations
The C language has two different ways to represent numbers, unsigned and
signed:
unsigned: can only represent non-negative numbers
signed: can represent negative, zero, and positive numbers
We are going to talk about these representations, and also about what happens
when we expand or shrink an encoded integer to fit into a different type (e.g., int
to long)
Unsigned Integers
For positive (unsigned) integers, there is a 1-to-1 relationship between the
decimal representation of a number and its binary representation. If you have a
4-bit number, there are 16 possible combinations, and the unsigned numbers go
from 0 to 15:
0b0000 = 0 0b0001 = 1 0b0010 = 2 0b0011 = 3
0b0100 = 4 0b0101 = 5 0b0110 = 6 0b0111 = 7
0b1000 = 8 0b1001 = 9 0b1010 = 10 0b1011 = 11
0b1100 = 12 0b1101 = 13 0b1110 = 14 0b1111 = 15
The range of an unsigned number is 0 → 2w- 1, where wis the number of bits
in our integer. For example, a 32-bit int can represent numbers from 0 to
232 - 1, or 0 to 4,294,967,295.
Signed Integers: How do we represent them?
What if we want to represent negative numbers? We have choices!
One way we could encode a negative number is simply to designate some bit as
a "sign" bit, and then interpret the rest of the number as a regular binary number
and then apply the sign. For instance, for a four-bit number:
0 001 = 1
0 010 = 2
0 011 = 3
0 100 = 4
0 101 = 5
0 110 = 6
0 111 = 7
1 001 = -1
1 010 = -2
1 011 = -3
1 100 = -4
1 101 = -5
1 110 = -6
1 111 = -7
This might be okay...but we've only represented 14 of our 16 available numbers...
Signed Integers: How do we represent them?
0 001 = 1
0 010 = 2
0 011 = 3
0 100 = 4
0 101 = 5
0 110 = 6
0 111 = 7
1 001 = -1
1 010 = -2
1 011 = -3
1 100 = -4
1 101 = -5
1 110 = -6
1 111 = -7
What about 0 000 and 1 000? What should
they represent?
Well...this is a bit tricky!
Signed Integers: How do we represent them?
0 001 = 1
0 010 = 2
0 011 = 3
0 100 = 4
0 101 = 5
0 110 = 6
0 111 = 7
1 001 = -1
1 010 = -2
1 011 = -3
1 100 = -4
1 101 = -5
1 110 = -6
1 111 = -7 0 000 1 000Let's look at the bit patterns:
What about 0 000 and 1 000? What should
they represent?
Well...this is a bit tricky!
Should we make the 0 000 just represent decimal 0? What about 1 000? We
could make it 0 as well, or maybe -8, or maybe even 8, but none of the choices
are nice.
Signed Integers: How do we represent them?
0 001 = 1
0 010 = 2
0 011 = 3
0 100 = 4
0 101 = 5
0 110 = 6
0 111 = 7
1 001 = -1
1 010 = -2
1 011 = -3
1 100 = -4
1 101 = -5
1 110 = -6
1 111 = -7 0 000 1 000Let's look at the bit patterns:
Should we make the 0 000 just represent decimal 0? What about 1 000? We
could make it 0 as well, or maybe -8, or maybe even 8, but none of the choices
are nice.
What about 0 000 and 1 000? What should
they represent?
Well...this is a bit tricky!
Fine. Let's just make 0 000 to be equal to decimal 0. How does arithmetic
work?
Well…to add two numbers, you need to know the sign, then you might have to
subtract (borrow and carry, etc.), and the sign might change…this is going to
get ugly!

Signed Integers: How do we represent them?

Signed Integers: How do we represent them?
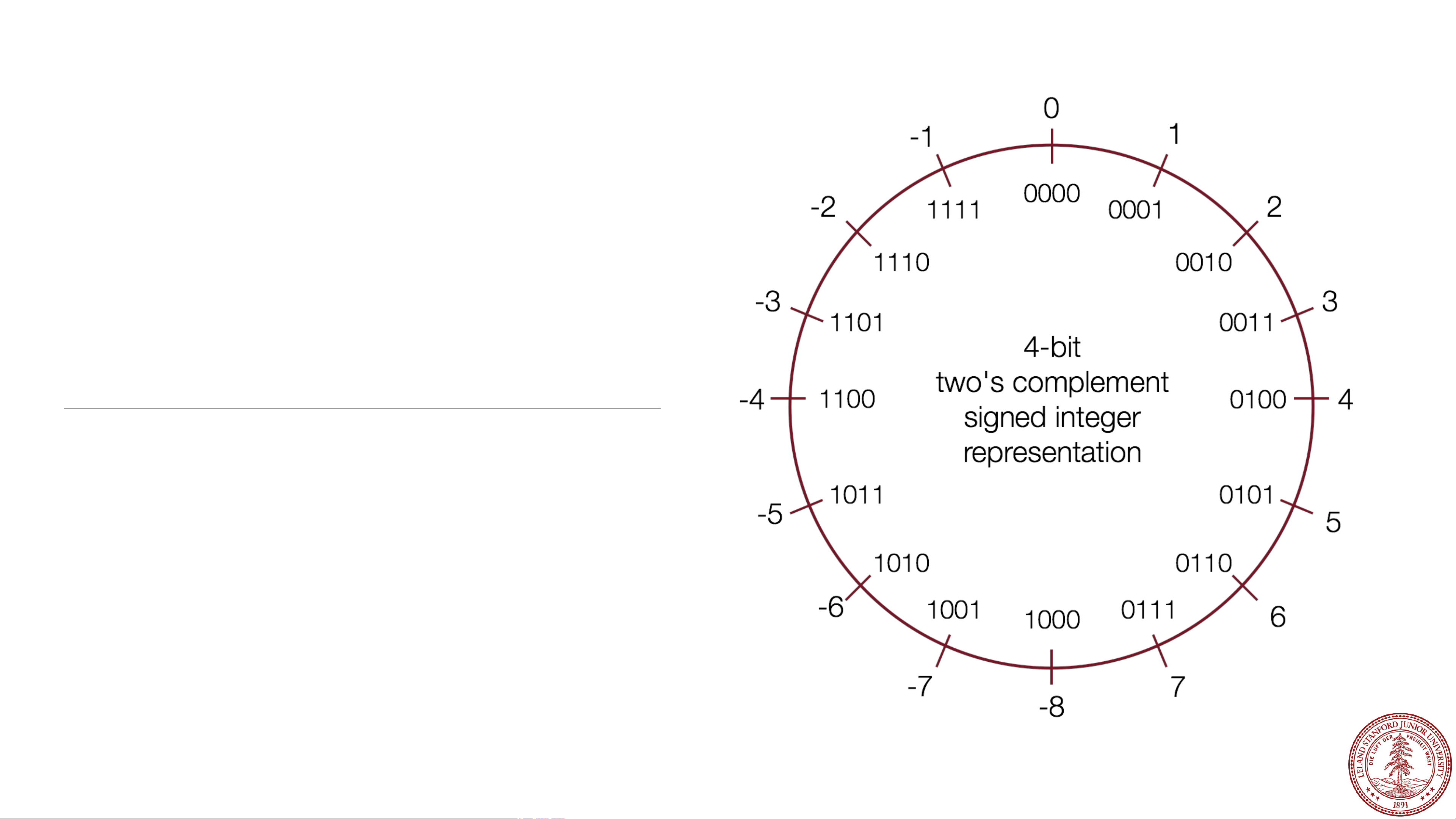
Behold: the "two's complement" circle:
In the early days of computing*, two's
complement was determined to be an
excellent way to store binary numbers.
In two's complement notation, positive
numbers are represented as
themselves (phew), and negative
numbers are represented as the two's
complement of themselves (definition
to follow).
This leads to some amazing arithmetic
properties!
*John von Neumann suggested it in 1945, for the EDVAC
computer.

Two's Complement
In practice, a negative number in two's complement is obtained by
inverting all the bits of its positive counterpart*, and then adding 1.
*Inverting all the bits of a number is its "one's complement"
Definition:
A two's-complement number system encodes positive
and negative numbers in a binary number
representation. The weight of each bit is a power of two,
except for the most significant bit, whose weight is the
negative of the corresponding power of two.
B2Twmeans "Binary to Two's complement function"
Two's Complement
In practice, a negative number in two's
complement is obtained by inverting all
the bits of its positive counterpart*, and
then adding 1, or: x = ~x + 1
*Inverting all the bits of a number is its "one's complement"
Example: The number 2 is represented as normal in
binary: 0010
-2 is represented by inverting the bits, and adding 1:
0010 ☞1101
1101
+ 1
1110
Two's Complement
Trick: to convert a positive number to
its negative in two's complement, start
from the right of the number, and write
down all the digits until you get to a 1.
Then invert the rest of the digits:
*Inverting all the bits of a number is its "one's complement"
Example: The number 2 is represented as normal in
binary: 0010
Going from the right, write down numbers until you
get to a 1:
10
Then invert the rest of the digits:
1110
Two's Complement
To convert a negative number to a
positive number, perform the same
steps!
Example: The number -5 is represented in two's
complements as: 1011
5 is represented by inverting the bits, and adding 1:
1011 ☞0100
0100
+ 1
0101
Shortcut: start from the right, and write down
numbers until you get to a 1:
1
Now invert all the rest of the digits:
0101
Two's Complement: Neat Properties
There are a number of useful
properties associated with two's
complement numbers:
1. There is only one zero (yay!)
2. The highest order bit (left-most) is 1
for negative, 0 for positive (so it is
easy to tell if a number is negative)
3. Adding two numbers is
just…adding!
Example:
2 + -5 = -3
0010 ☞2
+1011 ☞-5
1101 ☞-3 decimal (wow!)
Two's Complement: Neat Properties
More useful properties:
4. Subtracting two numbers is simply
performing the two's complement
on one of them and then adding.
Example:
4 - 5 = -1
0100 ☞4, 0101 ☞5
Find the two's complement of 5: 1011
add:
0100 ☞4
+1011 ☞-5
1111 ☞-1 decimal
Two's Complement: Neat Properties
More useful properties:
5. Multiplication of two's complement
works just by multiplying (throw
away overflow digits).
Example: -2 * -3 = 6
1110 ☞-2
x1101 ☞-3
1110
0000
1110
+1110
10110110 ☞6
Two's Complement: Powers of two remain!
From the definition of a two's
complement number, we can see that we
are still dealing with bits being equal to
their powers-of-two place: there isn't
anything magical about the placement of
the bits:
-5 = 1 0 1 1
(1 * -23) + (0 * 22) + (1 * 21) + (1 * 20)
Practice
Convert the following 4-bit numbers
from positive to negative, or from
negative to positive using two's
complement notation:
a. -4 (1100) ☞
b. 7 (0111) ☞
c. 3 (0011) ☞
d. -8 (1000) ☞
Practice
Convert the following 4-bit numbers
from positive to negative, or from
negative to positive using two's
complement notation:
a. -4 (1100) ☞
b. 7 (0111) ☞
c. 3 (0011) ☞
d. -8 (1000) ☞
0100
1001
1101
1000 (?! If you look at
the chart, +8 cannot be represented
in two's complement with 4 bits!)
Practice
Convert the following 8-bit numbers
from positive to negative, or from
negative to positive using two's
complement notation:
a. -4 (11111100) ☞
b. 27 (00011011) ☞
c. -127 (10000001) ☞
d. 1 (00000001) ☞
00000100
11100101
01111111
11111111
Casting Between Signed and Unsigned
Converting between two numbers in C can happen explicitly (using a
parenthesized cast), or implicitly (without a cast):
int tx, ty;
unsigned ux, uy;
…
tx = (int) ux;
uy = (unsigned) ty;
1
2
3
4
5
int tx, ty;
unsigned ux, uy;
…
tx = ux; // cast to signed
uy = ty; // cast to unsigned
1
2
3
4
5
explicit implicit
When casting: the underlying bits do not change, so there isn't any
conversion going on, except that the variable is treated as the type that it is.
You cannot convert a signed number to its unsigned counterpart using a
cast!
Casting Between Signed and Unsigned
// test_cast.c
#include<stdio.h>
#include<stdlib.h>
int main() {
int v = -12345;
unsigned int uv = (unsigned int) v;
printf("v = %d, uv = %u\n",v,uv);
return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
$ ./test_cast
v = -12345, uv = 4294954951
When casting: the underlying bits do not change, so there isn't any
conversion going on, except that the variable is treated as the type that it is.
You cannot convert a signed number to its unsigned counterpart using a
cast!
Casting Between Signed and Unsigned
int x = -1;
unsigned u = 3000000000; // 3 billion
printf("x = %u = %d\n", x, x);
printf("u = %u = %d\n", u, u);
1
2
3
4
5
6
7
8
9
10
11
$ ./test_printf
x = 4294967295 = -1
u = 3000000000 = -1294967296
printf has three 32-bit integer representations:
%d : signed 32-bit int
%u : unsigned 32-bit int
%x : hex 32-bit int
As long as the value is a 32-bit type, printf will treat it according to the
formatter it is applying:

Signed vs Unsigned Number Wheels
Comparison between signed and unsigned
integers
When a C expression has combinations of signed and unsigned variables,
you need to be careful!
If an operation is performed that has both a signed and an unsigned value,
C implicitly casts the signed argument to unsigned and performs the
operation assuming both numbers are non-negative. Let's take a look…
Expression Type Evaluation
0 == 0U
-1 < 0
-1 < 0U
2147483647 > -2147483647 - 1
2147483647U > -2147483647 - 1
2147483647 > (int)2147483648U
-1 > -2
(unsigned)-1 > -2
Comparison between signed and unsigned
integers
When a C expression has combinations of signed and unsigned variables,
you need to be careful!
If an operation is performed that has both a signed and an unsigned value,
C implicitly casts the signed argument to unsigned and performs the
operation assuming both numbers are non-negative. Let's take a look…
Expression Type Evaluation
0 == 0U Unsigned 1
-1 < 0 Signed 1
-1 < 0U Unsigned 0
2147483647 > -2147483647 - 1 Signed 1
2147483647U > -2147483647 - 1 Unsigned 0
2147483647 > (int)2147483648U Signed 1
-1 > -2 Signed 1
(unsigned)-1 > -2 Unsigned 1

Comparison between signed and unsigned
integers
Let's try some more…a bit more abstractly.
int s1, s2, s3, s4;
unsigned int u1, u2, u3, u4;
Which many of the following
statements are true? (assume that
variables are set to values that place
them in the spots shown)
s3 > u3
u2 > u4
s2 > s4
s1 > s2
u1 > u2
s1 > u3

Comparison between signed and unsigned
integers
Let's try some more…a bit more abstractly.
int s1, s2, s3, s4;
unsigned int u1, u2, u3, u4;
Which many of the following
statements are true? (assume that
variables are set to values that place
them in the spots shown)
s3 > u3 : true
u2 > u4 : true
s2 > s4 : false
s1 > s2 : true
u1 > u2 : true
s1 > u3 : true
The sizeof Operator
As we have seen, integer types are limited by the number of bits they hold. On
the 64-bit myth machines, we can use the sizeof operator to find how many
bytes each type uses:
int main() {
printf("sizeof(char): %d\n", (int) sizeof(char));
printf("sizeof(short): %d\n", (int) sizeof(short));
printf("sizeof(int): %d\n", (int) sizeof(int));
printf("sizeof(unsigned int): %d\n", (int) sizeof(unsigned int));
printf("sizeof(long): %d\n", (int) sizeof(long));
printf("sizeof(long long): %d\n", (int) sizeof(long long));
printf("sizeof(size_t): %d\n", (int) sizeof(size_t));
printf("sizeof(void *): %d\n", (int) sizeof(void *));
return 0;
}
$ ./sizeof
sizeof(char): 1
sizeof(short): 2
sizeof(int): 4
sizeof(unsigned int): 4
sizeof(long): 8
sizeof(long long): 8
sizeof(size_t): 8
sizeof(void *): 8
Type Width in bytes Width in bits
char 1 8
short 216
int 432
long 864
void * 8 64
MIN and MAX values for integers
Because we now know how bit patterns for integers works, we can figure out
the maximum and minimum values, designated by INT_MAX, UINT_MAX,
INT_MIN, (etc.), which are defined in limits.h
Type Width
(bytes)
Width
(bits) Min in hex (name) Max in hex (name)
char 1 8 80 (CHAR_MIN) 7F (CHAR_MAX)
unsigned char 1 8 0 FF (UCHAR_MAX)
short 216 8000 (SHRT_MIN) 7FFF (SHRT_MAX)
unsigned short 216 0 FFFF (USHRT_MAX)
int 432 80000000 (INT_MIN) 7FFFFFFF (INT_MAX)
unsigned int 432 0FFFFFFFF (UINT_MAX)
long 864 8000000000000000 (LONG_MIN) 7FFFFFFFFFFFFFFF (LONG_MAX)
unsigned long 864 0FFFFFFFFFFFFFFFF (ULONG_MAX)
Expanding the bit representation of a number
Sometimes we want to convert between two integers having different sizes.
E.g., a short to an int, or an int to a long.
We might not be able to convert from a bigger data type to a smaller data
type, but we do want to always be able to convert from a smaller data type
to a bigger data type.
This is easy for unsigned values: simply add leading zeros to the
representation (called "zero extension").
unsigned short s = 4;
// short is a 16-bit format, so s = 0000 0000 0000 0100b
unsigned int i = s;
// conversion to 32-bit int, so i = 0000 0000 0000 0000 0000 0000 0000 0100b
Expanding the bit representation of a number
For signed values, we want the number to remain the same, just with more
bits. In this case, we perform a "sign extension" by repeating the sign of the
value for the new digits. E.g.,
short s = 4;
// short is a 16-bit format, so s = 0000 0000 0000 0100b
int i = s;
// conversion to 32-bit int, so i = 0000 0000 0000 0000 0000 0000 0000 0100b
—or —
short s = -4;
// short is a 16-bit format, so s = 1111 1111 1111 1100b
int i = s;
// conversion to 32-bit int, so i = 1111 1111 1111 1111 1111 1111 1111 1100b
Sign-extension Example
// show_bytes() defined on pg. 45, Bryant and O'Halloran
int main() {
short sx = -12345; // -12345
unsigned short usx = sx; // 53191
int x = sx; // -12345
unsigned ux = usx; // 53191
printf("sx = %d:\t", sx);
show_bytes((byte_pointer) &sx, sizeof(short));
printf("usx = %u:\t", usx);
show_bytes((byte_pointer) &usx, sizeof(unsigned short));
printf("x = %d:\t", x);
show_bytes((byte_pointer) &x, sizeof(int));
printf("ux = %u:\t", ux);
show_bytes((byte_pointer) &ux, sizeof(unsigned));
return 0;
}
$ ./sign_extension
sx = -12345: c7 cf
usx = 53191: c7 cf
x = -12345: c7 cf ff ff
ux = 53191: c7 cf 00 00
(careful: this was printed
on the little-endian myth
machines!)
Back to right shift: arithmetic -vs- logical
Recall that the right-shift (>>)
operator behaves differently for
unsigned and signed numbers:
•Unsigned numbers are
logically-right shifted (by
shifting in 0s, always)
•Signed numbers are
arithmetically-right shifted (by
shifting in the sign bit)
// show_bytes() defined on pg. 45, Bryant and O'Halloran
int main() {
int a = 1048576;
int a_rs8 = a >> 8;
int b = -1048576;
int b_rs8 = b >> 8;
printf("a = %d:\t", a);
show_bytes((byte_pointer) &a, sizeof(int));
printf("a >> 8 = %d:\t", a_rs8);
show_bytes((byte_pointer) &a_rs8, sizeof(int));
printf("b = %d:\t", b);
show_bytes((byte_pointer) &b, sizeof(int));
printf("b >> 8 = %d:\t", b_rs8);
show_bytes((byte_pointer) &b_rs8, sizeof(int));
return 0;
}
$ ./right_shift
a = 1048576: 00 00 10 00
a >> 8 = 4096: 00 10 00 00
b = -1048576: 00 00 f0 ff
b >> 8 = -4096: 00 f0 ff ff
(run on a little-endian machine)
Truncating Numbers: Signed
What if we want to reduce the
number of bits that a number
holds? E.g.
int x = 53191;
short sx = (short) x;
int y = sx;
What happens here? Let's look at the bits in x (a 32-bit int), 53191:
0000 0000 0000 0000 1100 1111 1100 0111
When we cast x to a short, it only has 16-bits, and C truncates the
number:
1100 1111 1100 0111
What is this number in decimal? Well, it must be negative (b/c of the initial
1), and it is -12345.
Truncating Numbers: Signed
What if we want to reduce the
number of bits that a number
holds? E.g.
int x = 53191; // 53191
short sx = (short) x; // -12345
int y = sx;
This is a form of overflow! We have altered the value of the number.
Be careful!
We don't have enough bits to store the int in the short for the value we
have in the int, so the strange values occur.
What is y above? We are converting a short to an int, so we sign-extend,
and we get -12345!
1100 1111 1100 0111 becomes
Play around here: http://www.convertforfree.com/twos-complement-calculator/
1111 1111 1111 1111 1100 1111 1100 0111
Truncating Numbers: Signed
If the number does fit into the
smaller representation in the
current form, it will convert just
fine.
int x = -3; // -3
short sx = (short) -3; // -3
int y = sx; // -3
x: 1111 1111 1111 1111 1111 1111 1111 1101 becomes
Play around here: http://www.convertforfree.com/twos-complement-calculator/
sx: 1111 1111 1111 1101
Truncating Numbers: Unsigned
We can also lose information
with unsigned numbers:
unsigned int x = 128000;
unsigned short sx = (short) x;
unsigned int y = sx;
Bit representation for x = 128000 (32-bit unsigned int):
0000 0000 0000 0001 1111 0100 0000 0000
Truncated unsigned short sx:
1111 0100 0000 0000
which equals 62464 decimal.
Converting back to an unsigned int, y = 62464
Overflow in Unsigned Addition
When integer operations overflow in C, the runtime does not produce an error:
#include<stdio.h>
#include<stdlib.h>
#include<limits.h> // for UINT_MAX
int main() {
unsigned int a = UINT_MAX;
unsigned int b = 1;
unsigned int c = a + b;
printf("a = %u\n",a);
printf("b = %u\n",b);
printf("a + b = %u\n",c);
return 0;
}
$ ./unsigned_overflow
a = 4294967295
b = 1
a + b = 0
Technically, unsigned integers in C don't
overflow, they just wrap. You need to be
aware of the size of your numbers. Here is
one way to test if an addition will fail:
// for addition
#include <limits.h>
unsigned int a = <something>;
unsigned int x = <something>;
if (a > UINT_MAX - x) /* `a + x` would overflow */;

Overflow in Signed Addition
Signed overflow wraps around to the negative numbers:
YouTube fell into this trap —their view counter was a signed, 32-bit int. They
fixed it after it was noticed, but for a while, the view count for Gangnam Style
(the first video with over INT_MAX number of views) was negative.
Overflow in Signed Addition
Signed overflow wraps around to the negative numbers.
$ ./signed_overflow
a = 2147483647
b = 1
a + b = -2147483648
#include<stdio.h>
#include<stdlib.h>
#include<limits.h> // for INT_MAX
int main() {
int a = INT_MAX;
int b = 1;
int c = a + b;
printf("a = %d\n",a);
printf("b = %d\n",b);
printf("a + b = %d\n",c);
return 0;
}
Technically, signed integers in C produce
undefined behavior when they overflow. On
two's complement machines (virtually all
machines these days), it does overflow
predictably. You can test to see if your addition
will be correct:
// for addition
#include <limits.h>
int a = <something>;
int x = <something>;
if ((x > 0) && (a > INT_MAX - x)) /* `a + x` would overflow */;
if ((x < 0) && (a < INT_MIN - x)) /* `a + x` would underflow */;
References and Advanced Reading
•References:
•Two's complement calculator: http://www.convertforfree.com/twos-complement-
calculator/
•Wikipedia on Two's complement:
https://en.wikipedia.org/wiki/Two%27s_complement
•The sizeof operator: http://www.geeksforgeeks.org/sizeof-operator-c/
•Advanced Reading:
•Signed overflow: https://stackoverflow.com/questions/16056758/c-c-unsigned-
integer-overflow
•Integer overflow in C: https://www.gnu.org/software/autoconf/manual/autoconf-
2.62/html_node/Integer-Overflow.html
•https://stackoverflow.com/questions/34885966/when-an-int-is-cast-to-a-short-and-
truncated-how-is-the-new-value-determined
01
2
3
4
-1
-2
-3
-4
7
6
5
-7
-6
-5
-8
0000 0001
0010
0011
0100
0101
0110
0111
1111
1110
1101
1100
1011
1010
1001 1000
4-bit
two's complement
signed integer
representation
01
2
3
4
15
14
13
12
7
6
5
9
10
11
8
0000 0001
0010
0011
0100
0101
0110
0111
1111
1110
1101
1100
1011
1010
1001 1000
4-bit
unsigned integer
representation
