CS 101
Data and Storage
Recap from last time
Plan for today
Today, we'll learn how computers store information ("data"). We'll also learn how we can manipulate data in code.
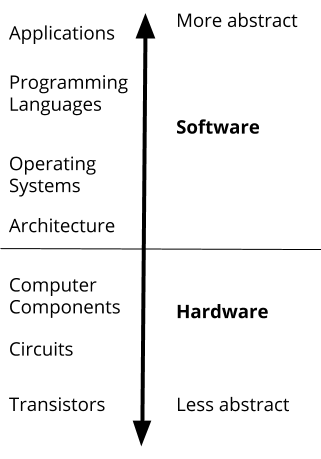
Bits
- Recall: transistors are on or off (two states)
- Use binary (base 2) instead of decimal (base 10)
- "Bit": 0 or 1 (off/on)
- Equivalent to digit in decimal
- How many numbers can we store with 1 bit? 2? 10?
| Decimal | 0 |
| Binary | 0 |
Bytes and Words
- Individual bits aren't that useful
- Solution: group 8 bits together into bytes
- Optimized to handle bytes instead of bits
- Hexadecimal vs. binary
- Group 4 or 8 bytes together to make a word
- Number of bits the CPU reads from memory at a time
- Part of the architecture
Representing Data: Characters
- Plain text uses ASCII (a numbering system for characters)
- Recall: ASCII art
- Each character is represented by one byte (8 bits)
- Unicode
- Used for representing "special" characters and emojis
- Controlled by The Unicode Consortium
- Represented with two bytes (65,536 combinations)
- Unicode Consortium controls emojis - lots of controversy over which emojis to make official
- Words are just a sequence of characters (computers use ASCII when possible)
Representing Data: ASCII
Representing Data: Integers
- Represented with one computer word (32 or 64 bits)
- Problems with 32 bits:
- Not enough options to label all computers in the world
- Gangnam Style "overflow"

Source: http://www.exploringbinary.com/gangnam-style-video-overflows-youtube-counter/
Representing Data: Adding Integers
- Adding integers in binary is exactly like adding integers in decimal
- Examples:
0101 (5) + 0111 (7)
0101 (5) + 1011 (11)
0111 (7) + 0011 (3)
Representing Data: Real Numbers
- Usually called doubles
- Represented with one computer word
- Much like scientific notation (IEEE Floating Point)
- Keeps track of the sign, the exponent, and the fractional part
- Idea: 7.5 can be represented as
1.875*2^2
- Tradeoff: fixed number of bytes means not perfectly precise
Lots of Bytes
- Fact: 2^10 is 1024 (about 1000)
- 1 kilobyte (KB) = 1024 bytes
- About the size of a 1000 character (200-250 word) paper
- Measures emails and text documents (each email is about 2KB)
- 1 megabyte (MB) = 1024KB (about 1 million bytes)
- MP3 audio is about 1 MB per minute
- Used to measure audio clips and image sizes
- 1 gigabyte (GB) = 1024MB (about 1 billion bytes)
- 1 hour of video is about 2GB
- Used to measure video sizes and computer storage space
- 1 terabyte (TB) = 1024GB (about 1 trillion bytes)
- Used to measure computer storage space
- Sometimes used in the context of "big data", along with petabytes (1024TB)
Storage space practice
| Word Problems | Solution |
|---|---|
| Alice has 600 MB of data. Bob has 700 MB of data. Will it all fit on Alice's 2 GB thumb drive? |
Yes it fits: 600 MB + 700 MB is 1300 MB. 1300 MB is 1.3 GB, so it will fit on the 2 GB drive no problem. Equivalently we could say that the 2 GB drive has space for 2000 MB, so the 1300 MB fits.
|
| Alice has 100 small images, each of which is 500 KB. How much space do they take up overall in MB? |
100 times 500 KB is 50000 KB, which is 50 MB.
|
| Your ghost hunting group is recording the sound inside a haunted Stanford classroom for 20 hours as MP3 audio files. About how much data will that be, expressed in GB? |
MP3 audio takes up about 1 MB per minute. 20 hours, 60 minutes/hour, 20 * 60 yields 1200 minutes. So that's about 1200 MB, which is 1.2 GB.
|
Megabytes vs. Mebibyte
- Marketers like to interpret a megabyte as 1 million bytes (less memory to make)
- Mebibyte is the actual 1024 * 1024 bytes
Data Compression
- Compression involves storing information using fewer bytes
- Lossless vs. lossy compression
- Original data
- 12000, 12002, 12006, 12007, 12010, 12006, 12005
- One potential lossless scheme - store differences:
- 12000, +2, +4, +1, +3, -4, -1
- One potential lossy scheme: store every other number
- 12000, (xxx), 12006, (xxx), 12010, (xxx), 12005
- Recreated data: 12000, (12003), 12006, (12008), 12010, (12007), 12005
Huffman Compression
- Lossless text compression
- Idea: not every letter is used equally
- Give each character a custom encoding
- More frequent characters get shorter encodings, z and q get encodings longer than a byte
- Note: computers are fastest at reading at the byte level
| Character | ASCII value | ASCII (binary) | Huffman (binary) |
|---|---|---|---|
' ' |
32 |
00100000 |
10 |
'a' |
97 |
01100001 |
0001 |
'b' |
98 |
01100010 |
0111010 |
'c' |
99 |
01100011 |
001100 |
'e' |
101 |
01100101 |
1100 |
'z' |
122 |
01111010 |
00100011010 |
Source: Marty Stepp
Other compression schemes
| Scheme | Lossless vs. Lossy? | Medium | Notes |
|---|---|---|---|
| MP3 | Lossy | Audio | 10x less space, but still sounds good |
| JPEG | Lossy | Images | Free and open source; very widely used and supported |
| GIF and PNG | Lossless | Images | PNG is a little bit better;mostly used for non-photographs |
Lossy Compression

|

|
The image on the right has been extremely compressed, taking up about 29% of the space as the image on the left.
Announcements
- A note on the readings (they're optional)
- First homework due tomorrow
- Thanks to Shreya for covering Thursday's lecture!
- Please email Shreya and me if you need any accommodations
Recall: Coding
Code: Variables
- Variable: a name for a piece of memory
- Quickly change code output
- Store value for easy access
- Name (
myName) without spaces and value ("Ashley Taylor") - Change value with an equals (
=) sign
Code: Getting input
- Already seen output
- Input keyword:
prompt - The argument is the question you ask the user
A very fancy calculator
- Variables can store numbers too
- Math operations work as normal:
+ - * / - Use
=to store the result
You try it!
- Write code to ask the user for two numbers, then print their sum.
- Hint:
parseInt("4")gives you the number 4
- Hint:
Conclusions
- Computers store data in bits using binary.
- Collections of bits are more useful for communicating information.
- Different types of information are stored differently. Data can be compressed to maximize storage space.
- We can label places in memory using variables.