CS 101
The Internet
Plan for Today
- Feedback
- Paper instructions
- How the internet works (how computers communicate and are connected):
- Abstraction
- Protocols (rules) for communication
Course Feedback
- As part of your next homework, please give us feedback on the course.
- Feedback is completely anonymous
- We really appreciate the opportunity to improve
Paper
- Information here
- Goal: demonstrate understanding of technical problems in society
- Goal: read and understand technical articles (at the level of WIRED, not research papers)
- Goal: weigh the advantages and disadvantages of new technology
- A fun series of comics that you might want to keep in mind as you write your paper
What is the Internet?
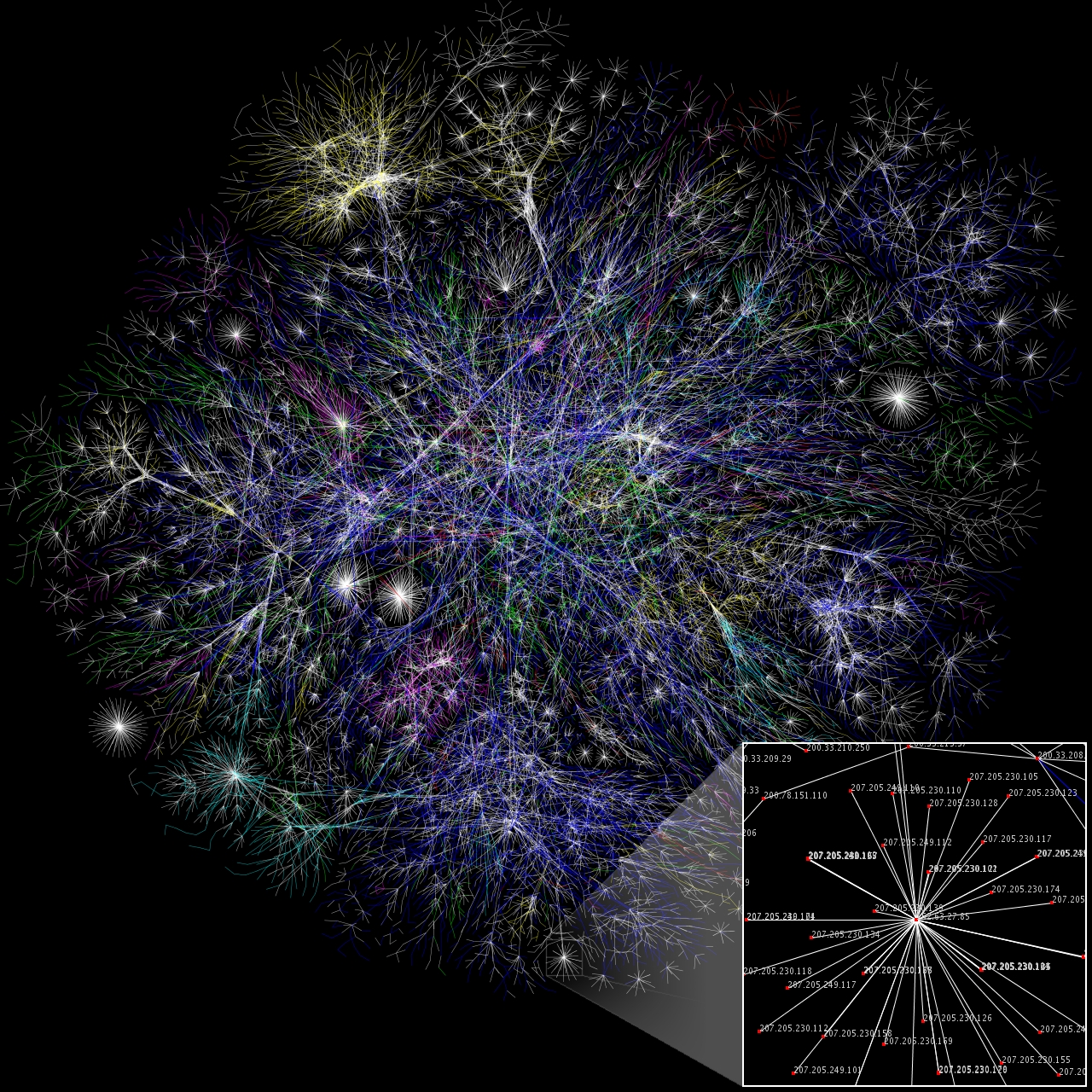
- A global system of computers connected together
- A network of networks!
- Designed to be redundant - can reach a computer through multiple paths
- Hierarchical - organized into ever smaller groups (like mail addresses)
- Internet allows computers to send information (bytes) to each other
Client-Server Model:
Loading a website
- Ask for a webpage (with a URL)
- Your computer (client) asks another computer at that URL (server) for the information (request)
- Request is sent to the server through a sequence of routers
- Server decodes the request, sends back the information (response)
- Client interprets the response
Accessing Information: URLs

- Uniform Resource Locator (URL)
- Protocol (rules for the information) (http)
- Domain name (gets converted to an IP address) via a Domain Name Server (DNS)
- IP address is computer-readable (e.g. 216.58.194.196 for google.com; 216.58.194.206 for images.google.com)
- Each byte of the address gets more specific, just like human mail addresses or URLs (Hierarchy)
- Try: 171.67.215.200/class/cs101/
Routers
- Each router is a gateway: connects one network to another
- LAN: Local Area Network
- Home router connects your LAN to the Internet Service Provider (ISP)
- Computers are connected on the internet through a sequence of routers (some for small areas, like LANs, others for larger areas)
- Hierarchy in networks
- Example: traceroute
Challenges of the Internet
Brainstorm some challenges of sending information over the internet
Challenges of the Internet
- How does the receiving computer know how to interpret the response?
- How to communicate across multiple operating systems?
- How do we know all the information was transferred?
- How do we handle lots of requests and responses to the same router at the same time?
- How do routers know where to send the information?
TCP/IP Protocol
- Rules for sending information between computers
- Followed by both clients and servers
- Developed by the Department of Defense, used by everyone
- Four layers of abstraction (most to least abstract)
- Application Protocol
- Transmission Control Protocol
- Internet Protocol
- Link Layer
Application Protocol
- Standardizes how different types of data (e.g. files, emails, http) are interpreted
- Way of interpreting the bits of data sent from one computer to another
- Http response codes
- 200s: all is good
- 400s: client errors
- 500s: server errors
Transmission Control Protocol (TCP)
- Separates the information into chunks (packets)
- Sends packets to receiver
- Reassembles the packets into the full request/response
- Figures out if packets are missing (checksum)
- Reorders packets
- Responsible for ensuring the information is complete and correct
Internet Protocol (IP)
- XX.XX.XX.XX (each XX is a byte) - you can Google for your IP address
- First byte is large area, and so on (hierarchical)
- Determines the path to send the packets (the next router to send to)
- Protocol for IP addresses
- Expanding to IPv6 (6 bytes of addresses instead of 4)
- Also includes Domain Name Servers (DNS)
- Convert from domains to IP addresses
- Internet Service Provider has DNS servers
- Kept up to date as IP addresses can change
Link Layer
- Converts between binary and network signals
- Wired uses Ethernet protocol
- Signals sent via voltages in a wire
- Wireless uses Wi-Fi protocol
- Signals sent via amplitude modulation of radio waves (like AM radio)
- Handles communication to/from router
- Note: packets are sent to every computer on the LAN at once
- Computers figure out which to listen to and which to ignore
Improving the Internet:
Content Distribution Networks (CDNs)
- Imagine millions of people go to hbo.com to watch Game of Thrones at once (real problem)
- Akamai and The Phantom Menace Trailer
- Redistribute requests and responses through routers to avoid traffic (like we do in cars)
- Cache (save) frequently requested resources
- Store the resource across multiple servers and route requests to servers with less "load" (less busy) or to servers closer to the client
Recap
- Recurring theme: abstraction (domain names and TCP/IP protocol)
- Internet is a connection of computers through routers
- Protocols define how computers interact with each other