For this project you will write 2-d algorithmic code to implement a kind of 2-d world of sand. What my kids have described as the world's worst version of Minecraft. When it's working, it's kind of fun to play and watch in its low-key way.
The starter code handles setting up the GUI window, and handling the controls and drawing. All the logic that makes the world work will be built by you.
All parts of HW3 are due Wed Jan 28th at 11:55 pm. To get started, download sand.zip.

We will use the simple CS106A Grid utility class to store the 2-d data. See Grid Reference
Using the Grid looks like this
grid = Grid(3, 2) # make 3 by 2 grid, initially all None grid.set(0, 0, 'hi') # set a value at 0,0 val = grid.get(0, 0) # get a value out at 0,0 if grid.in_bounds(4, 5): # is 4,5 in bounds? ...
We'll start with the waterfall problem as a warmup. Look at the file waterfall.py - there are two function for you to write.
In the waterfall grid every square is either rock 'r', water 'w', or empty None. Every turn, every water moves. The only question is, which way will the water move, or will it disappear from the world.
We'll decompose the problem into two functions — (a) dest_ok() checks boolean True/False if a destination square is available for a move, and (b) move_water() looks at a specific water and moves it.
def dest_ok(grid, x_to, y_to):
"""
Given a grid and possibly out-of-bounds x_to, y_to
return True if that destination is ok, False otherwise.
...
"""
The dest_ok() helper function checks if a particular x_to,y_to is a valid destination for water to move with the following checks:
1. If x_to,y_to is not in-bounds, the destination is not available, and nothing else needs to be checked.
2. If the x_to,y_to square is not empty, the destination is not available.
3. Otherwise, the destination is ok.
This function does not require much code and does not need any loops. There are several ways a destination might be unavailable. Therefore, one approach uses a series of if-statements to recognize and return False for each form of unavailable destination, with a final return True as the last line. If the move gets past all the if-statements, then the destination is ok.
We provide a set of Doctests in the starter code. Look them over, but you do not need to add any. Most of the Doctests use this grid as their input:
Use the Doctests to get this helper function working perfectly before moving on to the next step. Doctest pro-tip: when you have run a Doctest once, you can re-run it by clicking the green "play" button at the left-edge of the window. Running a Doctest again and again is the common pattern as you work on the functions like this, so you want to have a quick way to do it.
def move_water(grid, x_from, y_from):
"""
There is water at the given x_from, y_from.
Move the water to one of the 3 squares below,
or erase it, as described in the handout.
Return the grid when done.
(tests provided, code TBD)
>>> grid = Grid.build([['w', 'w', 'w'], ['r', None, 'w']])
>>> move_water(grid, 1, 0) # down ok
[['w', None, 'w'], ['r', 'w', 'w']]
...
"""
The move_water() function takes in the x_from, y_from of a square of water in the world and moves it in one of four ways and then returns the changed grid. There are no loops in this function. It works on a single x_from, y_from. Note: don't check if there is water at x_from,y_from just assume it is there, since that is the official precondition for move_water().
There are four possible moves for the water, checked in this order:
1. down If the square directly below the water is available for a move, move the water there and take no further actions. It's handy to use return grid to leave the function, avoiding the later steps. Move the water by setting its original square to None, and the new square to 'w'.
2. down-left If the square down-left is available, move the water there and take no further actions.
3. down-right If the square down-right is available, move the water there and take no further actions.
4. blocked If none of the three move above are available, the water disappears from the world.
In effect, the water tries down, down-left, down-right in that order, taking the first that works. If none of those work, the water disappears. In any case, return the changed grid.
CS106A mantra: use your helper function.
We provide basic Doctests which should be enough to get this working. Use the Doctests to perfect the code in this function before going on.
The Doctests use the same grid input as above:
For example, here is the first move_water() Doctest which tests a water which should go straight down:
>>> grid = Grid.build([['w', 'w', 'w'], ['r', None, 'w']])
>>> move_water(grid, 1, 0) # down ok
[['w', None, 'w'], ['r', 'w', 'w']]
It tries to move the middle water in the top row at (1, 0). The square immediately below that is empty, so the water should move from (1, 0) to (1, 1), resulting in the grid on the last line above.
Each Doctest needs to re-build the grid before calling move_water() .. why? This is necessary because each call to move_water() changes the grid. The later tests need a new grid, back in its initial state.
The "tall" Doctest checks that one run of move_water() moves the water only one square.
The move_water() function only does the work for a single x, y. A common question is — how is it that all the waters across the whole grid move? The following function is the answer.
The move_all_water() function is provided; please take a look at its code below so you see how the whole thing works. The function simply loops over the whole grid and calls your move_water() function to move each water it comes across:
def move_all_water(grid):
"""
Move every water 'w' in the world
once by calling move_water() for each.
(provided)
"""
for y in reversed(range(grid.height)):
for x in range(grid.width):
if grid.get(x, y) == 'w':
move_water(grid, x, y)
return grid
With the Doctests for your two functions passing, run the waterfall program from the command line. It's a little entrancing. If you look carefully, you should see the three cases. Water dodging to the left around rocks is common, and in rare cases water going to the right when hitting the right of two or more rocks, and very rarely water disappearing when hitting the middle of three or more rocks. You may need to run a few times to get a random world that exhibits all the cases.
$ python3 waterfall.py
Of course watching the program run in realtime, it's impossible to see that it's behaving correctly all the time. We use the small, frozen-in-time Doctests to really see (and debug!) code like this.
You can also add width and height numbers at the end of the command line to run a different size waterfall. The default is 50 by 30. Run a nice big world and see how long you can entrance your roommate into watching it. See if they can figure out all the rules just by watching it.
$ python3 waterfall.py 80 50
If the code crashes with some sort of an error (hardly an unusual occurrence), the error message will print in the command-line window. You have to look past the graphics window in front, seeing the error listing in the terminal. The error listing can be quite long. Read it from the bottom up, looking for the line that is in your code.
Sand is a more complicated and interactive program. We'll use the same divide-and-conquer strategy to divide the large program into many functions, and leverage Python's Doctests to test each function in isolation before moving on to the larger functions. You need to write five functions to make the whole thing work.
Every square in the Sand grid holds one of three things:
1. Sand represented by 's'
2. Rock represented by 'r'
3. Empty represented by None
In the sand world, each turn a sand 's' can move one square in one of five directions or stay where it is. First there are three basic moves: down, left, and right. These require only that the destination square is available. Then there are two diagonal moves, down-left and down-right, which have an additional constraint detailed later. Unlike waterfall, the sand does not disappear from the world.
The code for do_move() is provided. It's only two lines long. The """Docstring""" defines what this function does: move a sand from x_from,y_from to x_to,y_to, and return the changed grid to the caller. The function assumes that the move is legal (different code checks that first). Two Doctests are provided.
def do_move(grid, x_from, y_from, x_to, y_to):
"""
Given grid and x_from,y_from with a sand,
and x_to,y_to. Move the sand to x_to,y_to
and return the resulting grid.
Assume that this is a legal move: all coordinates are in
bounds, and x_to,y_to is empty.
(i.e. a different function checks that this is a
legal move before do_move() is called)
(provided code)
>>> grid = Grid.build([['r', 's', 's'], [None, None, None]])
>>> do_move(grid, 1, 0, 1, 1)
[['r', None, 's'], [None, 's', None]]
>>>
>>> grid = Grid.build([['r', 's', 's'], [None, None, None]])
>>> do_move(grid, 2, 0, 2, 1)
[['r', 's', None], [None, None, 's']]
"""
The code for do_move() is short, but it is good example of using Doctests to spell out test cases. Run the Doctests and they should pass.
The dest_ok() function can be called before a move to check if the "destination" x_to,y_to is available for a move. A square is ok for a move if it is in-bounds and is empty. This function should return True if x_to,y_to is ok for a move and False otherwise. (Other functions use both the "from" and "to" coordinates, but this one only needs the "to".) The code for this is the same or very similar to the code you built for waterfall, so you can copy that code to here and re-use it. Keep the Doctests here so we don't have inexplicable 'w' showing up in the sand tests.
Rather than being called for any move, diagonal_ok() should only be called for a diagonal move to check its specific constraints.
First, the destination of the diagonal move must be available. If the destination is not available, return False and no further checking is required.
If the destination is ok, the diagonal move must obey the corner rule, which requires that the "corner" square immediately above the destination square must be empty. Return False if the move violates the corner rule, and True otherwise.
For example in the following diagram, the diagonal down-left move is not ok because of the corner rule, and the diagonal down-right move is not ok because the destination is not ok.
The provided diagonal_ok() Doctest builds a 3x2 grid with two sand 's' in it. Each sand has two possible diagonal moves, down-left or down-right, so that's 4 possible diagonal moves total. One test is provided, moving the sand at (1, 0) down-left, which returns True since that move is ok. Add three more tests to cover the 3 other possible diagonal moves.
>>> grid = Grid.build([[None, 's', 's'], [None, None, None]])
>>> diagonal_ok(grid, 1, 0, 0, 1) # down-left ok, corner rule
True
Write the Doctests first, and then work on the code for diagonal_ok(). The code can assume that the coordinates describe a diagonal move, since that is the precondition for this function. This is a good time to make a drawing, sorting out the x's and y's to test the corner square. A reasonable structure for this function is a series if/return to detect the various ways the move might not be ok and return False, with a single return True at the bottom of the function.
Consider an x,y in the grid. The do_gravity() function implements one "gravity" move for that x,y to move any sand there one square as follows. In our gravity algorithm, the moves are handled in a specific order:
1. If there is not a sand 's' at x,y, do nothing, the move is over.
2. down: If the sand can move down to the square below, do it, and this ends the move. The down move needs only that the destination square is available.
3. down-left: otherwise if the sand can do a diagonal down-left move, do it, this ends the move.
4. down-right: otherwise if the sand can do a diagonal down-right move, do it, this ends the move.
In all cases, return the grid when the function is done. Use your helper functions to do the checking work. This function should not contain any loops. We provide a pretty thorough set of Doctests for this function, but of course you still need to write the code to actually solve the problem. You can add more tests, but it's not required.
A test may fail here because of a bug in your do_gravity() code, or because the run here exposes a previously undiscovered bug in your helper function. That happens sometimes. If the bug is in the helper, you might want to go back to the helper and add a test to get that code right, coming back here once the helper is sorted out.
For the moment, ignore the "brownian" parameter which is handled in a later step.
Write code and tests for a do_whole_grid() function which calls do_gravity() once for every x,y in the grid. This is the function that goes through all the x,y, calling your other functions. Return the grid when done. Write two tests, with at least one test featuring a 3x3 world with sand at the top row. In your test, pass 0 for the brownian parameter to do_whole_grid().
The standard y/x nested loops go through the coordinates top-down, and normally that's fine. However, in this case, it's important to reverse the y-direction, going bottom-up, i.e. visit the bottom row y = height-1 first, then y = height - 2, and so on with the top row y = 0 last. Suggestion: use the reversed() function.
What's wrong with regular top-down order? Suppose the loops went top-down, and at y=0, a sand moved from y=0 down to y=1 by gravity. Then when the loop got to y=1, that sand would get to move again. Going bottom-up avoids this problem.
Run your Doctests in do_whole_grid() to see that your code is plugged in and working correctly.
The do_whole_grid() does one "turn" of the world, calling do_gravity() a single time for each square. The provided GUI code calls this function again and again when the gravity checkmark is checked to make the game run.
With your functions tested, you can try running the whole program. Click the mouse button on a spot of the screen to scribble sand there. Gravity should work, but brownian is not done yet. Normally when a program runs the first time, there are many problems. But here we have leaned on decomposition and testing pretty hard, so there is a chance your code will work perfectly the first time. If your program works the first time, try to remember the moment. On projects where code is not so well tested, the first run of the program is often a mess. Having good tests changes the story.
Bring up the terminal and run the program like this (no command line arguments are required, on Windows its "py" or "python"):
$ python3 sand.py
Now for the last little bit of algorithm. Brownian motion is a real physical process, documented first by Robert Brown, who observed tiny pollen grains jiggling around on his microscope slide.
The "brownian" parameter is a number in the range 0..100 inclusive. When brownian is 20, that means there is a 20% chance that each sand will randomly try to move one square left or right each turn. The brownian number is taken in real time from the little slider at the top of the window, with the slider at the left meaning brownian=0 and at right meaning brownian=100. The Doctests are provided but you write the code (see below).
Here are the steps for the function do_brownian(grid, x, y, brownian):
1. Check if the square at x,y is sand. Proceed only if it is sand.
The Python function random.randrange(n) returns a random number uniformly distributed in the range 0..n-1. This is similar to the familiar range() function which is why "range" appears in the name of this function.
2. Create a random number in the range 0..99 with the following call.
num = random.randrange(100)
Proceed only if num < brownian. In this way, for example, if brownian is 50, we'll do the brownian move about 50% of the time.
3. Decide if the random move will be to the left or right. Set a "coin" variable like a coin flip with the following line. This lines sets coin to either 0 or 1:
coin = random.randrange(2)
4. If the coin is 0, try to move left. If the coin is 1, try to move right. Use your helper functions to check if the move is possible and do all the actual work (decomposition FTW). The coin indicates the direction for a single attempted move, and that's it. In this way the brownian motion is evenly balanced between left and right moves.
Testing an algorithm that behaves randomly is tricky. We have a little hack in the do_brownian() Doctest code that enables Docests there. The Doctest includes the following highly unusual line of code which we will further explain in week 9:
>>> # Hack: tamper with randrange() to always return 0
>>> # So we can write a test.
>>> # This only happens for the Doctest run, not in production.
>>> random.randrange = lambda n: 0
The line modifies the normal random.randrange() function so it returns 0 every time. Not exactly random! A couple tests are then written, knowing that the "random" value will always be zero when the Doctest runs. It's not a complete test, but it's better than nothing. When the code runs in production, the random numbers will behave normally.
Edit the loop body in do_whole_grid() so after do_gravity() for each x,y, it also calls do_brownian() for that x,y.
Try running the program with brownian switched on, which creates lively, less artificial look. Play around with the brownian slider to see your code in action.
You can provide 2 command line numbers to specify the number of squares wide and high for the grid. The default is 50 by 50 squares. So the following creates a grid 100 by 50
$ python3 sand.py 100 50
An optional third parameter specifies how many pixels wide each square should be. The default is 14. So this creates a 100 by 50 world with little 4 pixel squares, which changes the feel of the program.
$ python3 sand.py 100 50 4
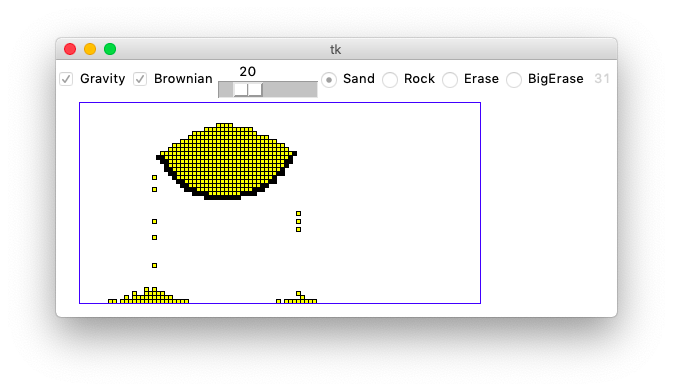
The Sand program is pretty demanding on your computer. It runs a lot of computation without pause. You may notice the fans on your laptop spinning up. At the upper right of the window is a little gray number, which is the frames-per-second (fps) the program is achieving at that moment, like 31 or 52. The animation has a more fluid look with fps of, say, 50 or higher.
The more grid squares there are, and the more grains of sand there are, the slower the program runs. For each gravity round, your code needs to at least glance at every square and every grain of sand. By making the world large or by adding lots of sand, the fps of the game should go down. Play around with different grid and pixel sizes to try out the different esthetics.
Once you get that all working, congratulations. That's a real program with complex logic, deep use of function decomposition and testing, and some neat output.
When your code is working and has good cleaned up style, please turn in your waterfall.py and sand.py on paperless as usual.
This assignment is based on the "Falling Sand" assignment by Dave Feinberg at the Stanford Nifty Assignment archive. Nick Parlante re-built it in Python, adding in the emphasis on 2-d testing and decomposition, and created the waterfall as a warmup. In 2026, separating out the diagonal_ok() from dest_ok(), hopefully making a cleaner design.