Today: parsing, complex while loops, parse words out of string patterns

Data and Parsing

Here's some fun looking data...

$GPGGA,005328.000,3726.1389,N,12210.2515,W,2,07,1.3,22.5,M,-25.7,M,2.0,0000*70
$GPGSA,M,3,09,23,07,16,30,03,27,,,,,,2.3,1.3,1.9*38
$GPRMC,005328.000,A,3726.1389,N,12210.2515,W,0.00,256.18,221217,,,D*78
$GPGGA,005329.000,3726.1389,N,12210.2515,W,2,07,1.3,22.5,M,-25.7,M,2.0,0000*71
$GPGSA,M,3,09,23,07,16,30,03,27,,,,,,2.3,1.3,1.9*38
$GPRMC,005329.000,A,3726.1389,N,12210.2515,W,0.00,256.18,221217,,,D*79
$GPGGA,005330.000,3726.1389,N,12210.2515,W,2,07,1.3,22.5,M,-25.7,M,3.0,0000*78
$GPGSA,M,3,09,23,07,16,30,03,27,,,,,,2.3,1.3,1.9*38
...

• The above is what a GPS chip outputs
• buried deep in your phone, this is going on
  It's a standard: NMEA_018
• Notice: it's just text
  a series of text lines ending with \n
  each line is made of chars
  We will use s.split(',') on lines like this later
• Text is a super common exchange format between systems
• "Parsing"
  Have raw text like this example
  Find and pull out the data you want
• On the surface, we are doing parsing examples today
• Really you want experience with loops and complex logic
  Parsing is just a handy domain

Things from last time, use today:

Recall 1: while Equivalent of for/range

The while-loop is more flexible than the for-loop. Here is the while-equivalent to for i in range(n)

i = 0         # 1. init
while i < n:  # 2. test
    # use i
    i += 1    # 3. update at loop-bottom
              # (easy to forget this line)

Recall 2 - When is i In Bounds?

Suppose the int i is indexing into a string, and I am changing it with i += 1 or i -= 1. What are the bounds for i remaining a valid index into the string?

In-bounds for increasing i:

i < length

In-bounds for decreasing i:

i >= 0

Python detail: surprisingly s[-1] does not give an error in Python, it accesses the last char, although this may not be what you want. For our algorithms, we treat i >= 0 as the boundary.

Foreshadow: Advance With var += 1

• Framing for today's example
• Imagine a text string on paper
• A finger is pointing at some char to start
• Move the finger to the right, say until pointing at a space char
• Python: have a var end with an index into string
• e.g. end is 4, pointing at the 'a'
• end += 1 .. like moving one to the right
• Continue end += 1 until get to a space

Start with end = 4. Advance to space char with end += 1 in loop

Aside - the CS106A Story Arc

• Have some problem IRL
• Think about what we want - a drawing or scheme about a data structure
• Think about steps on the drawing
• Translate into code
• Debug the code,
  Look at the error message
  Look at the drawing
• Add fixes to the code until it works
• Profit!
• Todays examples show every step

Example: at_word()

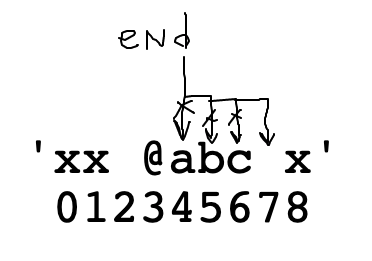
'xx @abcd xyz' -> 'abcd'
'x@ab^xyz' -> 'ab'

at_word(s): We'll say an at-word is an '@' followed by zero or more alphabetic chars. Find and return the alphabetic part of the first at-word in s, or the empty string if there is none. So 'xx @abc xyz' returns 'abc'.

• Realistic parsing problem, extracting the wanted part of a string
• Demonstrate several patterns on this one
• We'll re-use these patterns
• We'll work through this one carefully
• Points about this code:
  Use str.find() to locate each @
  Use while to skip over alpha chars to find end
  Use var < len(s) to protect use of s[var]
  Var names: search, at, end - try to keep things straight

at_word() Strategy 1

First use s.find() to locate the '@'. Then start end pointing to the right of the '@'.

at_word() Start Picture

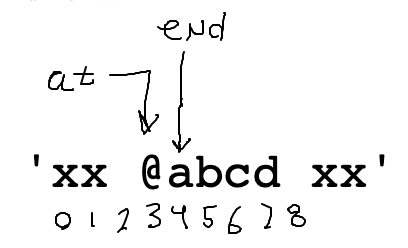
Code to set this up:

    at = s.find('@')
    if at == -1:
        return ''
    
    end = at + 1

at_word() Goal Picture

at_word() While Test

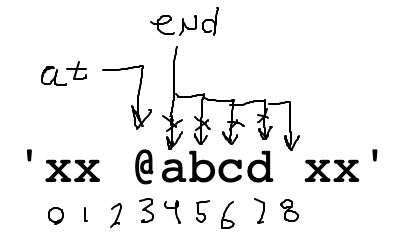
Use a while loop to advance end over the alphabetic chars. What is the test for this loop? Work it out on the drawing.

    while ???? 
        end += 1

• AKA skip over the alpha chars
• Loop test: this is true = advance end by one
• Test: s[end].isalpha()
• Reminisce : Bit "true = go" pattern for moving forward
• This code will 90% work, with one case to fix later
• Loop leaves end pointing to the first non-alpha char

This loop is 90% correct to advance end:

    # Advance end over alpha chars
    while s[end].isalpha():
        end += 1

at_word() Slice with end

Once we have at/end computed, pulling out the result word is just a slice.

    word = s[at + 1:end]
    return word

at_word() V1

Put those phrases together and it's an excellent first try, and it 90% works. Run it.

def at_word(s):
    at = s.find('@')
    if at == -1:
        return ''
    
    end = at + 1
    # Advance end over alpha chars
    while s[end].isalpha():
        end += 1

    word = s[at + 1:end]
    return word

at_word: 'woot' Bug

That code is pretty good, but there is actually a bug in the while-loop. It has to do with particular form of input case below, where the alphabetic chars go right up to the end of the string. Think about how the loop works when advancing "end" for the case below.

    at = s.find('@')
    end = at + 1
    while s[end].isalpha():
        end += 1

'xx@woot'
 01234567

Problem: keep advancing "end" .. past the end of the string, eventually end is 7. Then the while-test s[end].isalpha() throws an error since index 7 is past the end of the string.

The loop above translates to: "advance end so long as s[end] is alphabetic"

To fix the bug, we modify the test to: "advance end so long as end is valid and s[end] alphabetic".

In other words, stop advancing if end reaches the end of the string.

Loop end bug:

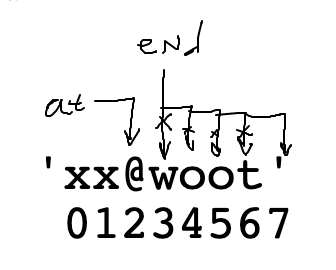
Solution: end < len(s) Guard Test

This "guard" pattern will be a standard part of looping over something. We cannot access s[end] when end is too big. Add a "guard" test end < len(s) before the s[end]. This stops the loop when end gets to 7. The slice then works as before. This code is correct.

def at_word(s):
    at = s.find('@')
    if at == -1:
        return ''

    # Advance end over alpha chars
    end = at + 1
    while end < len(s) and s[end].isalpha():
        end += 1
    
    word = s[at + 1:end]
    return word

Guard / Short Circuit Pattern

The "and" evaluates left to right. As soon as it sees a False it stops. In this way the < len(s) guard checks that "end" is a valid number, before s[end] tries to use it. This a standard pattern: the index-is-valid guard is first, then "and", then s[end] that uses the index. We'll see more examples of this guard pattern.

Loop / Guard Summary

With a loop that advances some index i to look in a string, add a i < len(s) guard to avoid going off the end of the string:

while i < len(s) and .... s[i] ...:
    i += 1`

Fix End Bug Recap

• Bug: run end off the end of s, testing non-existent s[end]
• e.g. this happens if input is s = 'xx @woot'
  Think through how the loop works for that case
• Solution:
• Add guard <
• This is the fixed loop:
  while end < len(s) and s[end].isalpha():
• Q: How to test if index i is valid in s?
• A: i < len(s)
• Only look at s[end] char after checking that end is valid
• Boolean Short Circuit
  Python evaluates expression left-right
  As soon as boolean value determined, stops trying
  A False in the midst of an and stops
  So the < guards the s[end].isalpha()

Note This Works ok: s[at + 1:end]

• Accessing s[end] off the end of the string is an error
  So we need the guard
• What about the slice s[at + 1:end]
• That actually works fine, for two reasons...

Reason 1 - UBNI

• Why does s[at + 1:end] work fine?
• Up To But Not Including - UBNI
• The char at the second index is not included in the slice
• So the fact that it's one past the end is fine - it is not included
• This is the best reason, so focus on this one

Reason 2 - Slice Tolerates Garbage

• The other reason it works is a little sketchy
• It turns out, slices never raise an error about bad out of bounds index numbers
• They will work with any old garbage numbers
• If a number is too big, it is interpreted as "the end of the string"
• This does not mean you can stop caring about index numbers
• It just means the slice is not checking for you
• Our above solution is fine - the end index is managed accurately
  Going exactly one past the chars we want in all cases

>>> s = 'Python'
>>> len(s)
6
>>> s[2:5]
'tho'
>>> s[2:6]
'thon'
>>> s[2:46789]
'thon'

at_words() - Zero Char Case - Works?

• What about 'xx @ xx'
• Consider slice of @ above
  s[at + 1:end]
  Turns out to be like s[4:4]
  Which is the empty string '', so the code we have works perfectly for this edge case

Example/Exercise: exclamation()

exclamation(s): We'll say an exclamation is zero or more alphabetic chars ending with a '!'. Find and return the first exclamation in s, or the empty string if there is none. So 'xx hi! xx' returns 'hi!'. (Like at_word, but right-to-left).

Set a variable start to the left of the exclamation mark. Move it left over the alphabetic chars.

Starter code

def exclamation(s):
    exclaim = s.find('!')
    if exclaim == -1:
        return ''

    # Your code here
    start = ???

Will need a guard here, as the loop goes right-to-left. The leftmost valid index is 0, so that will figure in the guard test.

exclamation() Solution

def exclamation(s):
    exclaim = s.find('!')
    if exclaim == -1:
        return ''
        
    # Your code here
    # Move start left over alpha chars
    # guard: start >= 0
    start = exclaim - 1
    while start >= 0 and s[start].isalpha():
        start -= 1
    
    # start is on the first non alpha
    word = s[start + 1:exclaim + 1]
    return word

Boolean Expressions

See the guide for details Boolean Expression

• Boolean operators: and or not
• Mixture of these, can add parenthesis to force order of operation
  "precedence" in CS parlance
• Say have three boolean variables, each True/False
  age - say age is good if less than 30
  is_raining - True if raining
  is_weekend- True if it's the weekend
• Define: to be a good day, need two things:
  1. it must not be raining
  2. then either age is under 30 or it's the weekend

The code below looks reasonable, but doesn't quite work right

def good_day(age, is_weekend, is_raining):
    if not is_raining and age < 30 or is_weekend:
        print('good day')

Boolean Precedence:

• "Precedence" is the order of operations
• not = highest, (like - in -7)
• and = next highest (like *)
• or = lowest (like +)

What The Above Does

Because and is higher precedence than or as written above, the code above acts like the following (and evaluates before or):

   if (not is_raining and age < 30) or is_weekend:

You can tell the above does not work right, because any time is_weekend is True, the whole thing is True, regardless of age or rain. This does not match the good-day definition above, which requires that it not be raining.

Boolean Precedence Solution

The solution we will spell out is not difficult.

• Many programmers do not have boolean precedence memorized .. fine
• Do remember that "not" is the highest precedence
• Solution: note when you have a mixture of and + or
  When there is a mixture, the precedence will matter
  put in parenthesis to set the order you want
• We will never complain about extra parenthesis, so add them to spell out the order you want
• In this case, put parens to group the or part, separating from not-raining
• BTW similar logic applies to math - if there's a mixture of * and +, add parenthesis

Solution

def good_day(age, is_weekend, is_raining):
    if not is_raining and (age < 30 or is_weekend):
        print('good day')

(optional) Exercise Boolean oh_no()

Parse "or" Example - at_word99()

'xx @ab12 xyz' -> 'ab12'

at_word99(): Like at-word, but with digits added. We'll say an at-word is an '@' followed by zero or more alphabetic or digit chars. Find and return the alpha-digit part of the first at-word in s, or the empty string if there is none. So 'xx @ab12 xyz' returns 'ab12'.

We've reached a very realistic level of complexity for solving real problems.

"end" Loop For at_words99()

Like before, but now a word is made of alpha or digit - many real problems will need this sort of code. This may be our most complicated line of code thus far in the quarter! Fortunately, it's a re-usable pattern for any of these "find end of xxx chars" problems.

The most difficult part is the "end" loop to locate where the word ends. What is the while test here? (Bring up at_word99() in other window to work it out). We want to use "or" to allow alpha or digit.

at = s.find('@')
end = at + 1
while ??????????:
    end += 1

at_word99() While Test

1. Still have the < guard
2. Use "or" to allow isalpha() or isdigit()
3. Need to add parens, since this has and+or
combination
while end < len(s) and (s[end].isalpha() or s[end].isdigit()):
    end += 1

at_word99() Solution

def at_word99(s):
    at = s.find('@')
    if at == -1:
        return ''

    # Advance end over alpha or digit chars
    # use "or" + parens
    end = at + 1
    while end < len(s) and (s[end].isalpha() or s[end].isdigit()):
        end += 1
    
    word = s[at + 1:end]
    return word

If we have time, we'll look at these.

(optional) Exercise: dotcom2()

 'xx www.foo.com xx' -> 'www.foo.com'

dotcomt2(s): We are looking for the name of an internet host within a string. Find the '.com' in s. Find the series of alphabetic chars or periods before the '.com' with a while loop and return the whole hostname, so 'xx www.foo.com xx' returns 'www.foo.com'. Return the empty string if there is no '.com'. This version has the added complexity of the periods.

Ideas: find the '.com', loop left-right to find the chars before it. Loop over both alphabetic and '.'

dotcom2() Solution

def dotcom2(s):
    com = s.find('.com')
    if com == -1:
        return ''
    
    # "or" logic - move leftwards over
    # alphabetic or '.'
    start = com - 1
    while start >= 0 and (s[start].isalpha() or s[start] == '.'):
        start -= 1
    
    return s[start + 1:com + 4]

Style: Long Lines

Normally each Python line of code is un-broken. BUT if you add parenthesis, Python allows the code to span multiple lines until the closing parenthesis. Indent the later lines an extra 4 spaces - in this way, they have a different indentation than the body of the while. There's also a preference to end each line with an operator like or .. to suggest that there's more on the later lines.

    while (end < len(s) and 
            (s[end].isalpha() or
            s[end].isdigit())):
        end += 1