Table of Content

• Overview of Our Approach
• Training and Testing Data
• Compressed File Structure
• Two classes of Coders
• Character-Level Coders
  • Naive
  • TrainedHuffman
  • AdaptiveHuffman
  • TrainedBigram
  • TrainedArithmetic
  • LZ
• Word-Level Coders
  • Huffman
  • AdaptiveHuffman
  • EnglishHuffman
  • Arithmetic
  • TrainedEncoder1
  • TrainedEncoder2
• Results
  • Comparing with gzip and bzip2
  • Experimenting with Different coders
  • Graphs and Tables
• Analysis of Failed Models
  • Normalization by Stemming
  • Normalization by Decapitalization
• Conclusion

Overview of Our Approach

The goal of this project is to investigate the numerous assumptions that can be made about the English language to help compress a large amount of English text efficiently and losslessly. The following is a list of generalizable properties of the English language we will attempt to exploit:

• The structure of the text follows an alternating [separator] [word] ... [word] [separator] pattern. "Separators", like spaces and newlines, tend to be more similar to each other than "words", and vice versa. We are hoping this implicit pattern reorders text to a more compressible form. Specifically, letting H be the information entropy function, we speculate that:

  H(text) > H(separators) + H(words)

  Because the alternating pattern is implicit, the cost of decomposition (i.e: bits to represent the decomposition) is free.
• Uncompressed, each character in a text file takes up 8 bits, but the fact is virtually all characters are confined to a small subset of the ASCII table, such as the English alphabets, numerals, and some punctuations. Any decent character-level coder should give us a lot of saving.
• The distribution of ASCII characters tends to generalize across different documents. For example, "e" and "i" always appear more frequently than "x" and "z". In fact, the bigram distributions also generalize, and should form a much better model in predicting the next character. An extreme example is the p(w2|w1='q') distribution, where p(w2='u'|w1='q') is going to be much greater than the norm.
• The frequency of terms in a document more or less follows Zipf's law, and that means it will be advantageous to do a word-level analysis, where more frequent terms are assigned shorter encodings.
• Stemming a word token into [canonical] [suffix] might be advantages similar to how the [separator] [word] ... [separator] pattern reorders text to a more compressionable state. The basic intuition is that words like "look" and "looked" will share the same dictionary entry, reducing the number of emittable symbols and thus shortening assigned encodings in general. The associated suffix dictionary should be small, so the suffix encodings ought to be minimal. We can further normalize a word token by representing its capitalization status separately, such that "The" and "the" will be shared in the main dictionary.

Eventually and surprisingly, we are able to cream gzip and even to beat bzip2 when compressing large English text.

Training and Testing Data

For some coders that require a language model, we preprocessed a bunch of New York Times articles from /afs/ir/data/linguistic-data/Newswire/nyt to form a unigram model. We concluded that a bigram model is too sparse to be beneficial. The same data was also used to train the ASCII distributions. To avoid the issue of overfitting our models, we used a set of test files provided by ACT Text Compression Test.

We have also gathered some big text files from Project Gutenberg to stress test the compression engine, and to see whether performance improves and degrades as the size of input files increase.

These test files will be hereby abbreviated as "anne", "musk" and "world95", "g161", and "mtent" in the rest of this report.

statistics of test files

name	size (bytes)
anne	586,969
musk	1,344,739
world95	2,988,578
g161	14,729,083
mtent	59,004,086

Compressed File Structure

The structure we have chosen is fairly straightforward. We have two independent streams of data in a compressed file:

1. Separator token stream
2. Word token stream

Note that all serialization and coding processes retain the "strictly causal" property in the signal processing sense. That means they do not need to skip around the bitstream, and need not even a single bit of lookahead. Such an requirement, or "prefix property", is imposed to minimize memory usage and facilitate modularity of the bitstream.

Following the serialized models, we have a gamma-coded number representing the number of word tokens N. The presence of this number makes encoding and decoding less complicated because we don't have to deal with "end markers" (i.e: needs escaping) denoting the end of a stream, but we pay for the convenience by having to make one extra pass over the input file in order to count tokens.

There are N word tokens but N+1 separator tokens. To generalize the process, we isolated the very first separator as a special case and encode it outside of the normal blockings.

Finally, we encode the blocks. Each block contains two sections corresponding to M separators and M word tokens tokens. Since there are a total of N word tokens, there are ceiling(N/M) number of blocks. Initially, we organized the file without blocking, or M=1. We had to change it to its current form because some coders to be efficient must process one large window at a time. For example, the Arithmetic coder must write a few trailing bits after each block. In this case, a large M means lower overhead, but at the same time, increases memory usage (though bounded) because the three streams each of length M must be buffered in memory for decomposition during compression, and reassembly during decompression.

top level structure

separator stream model (serialized separator coder)

word stream model (serialized word coder)

# of tokens N

first separator encoded

block 1

...

block N-1

block N

block k

M encoded separators

M encoded word tokens

Two Classes of Coders

In the top level, we have word-level coders that deal with data in unit of tokens. They are used to encode the separator or word streams one token at a time. For serialization purposes, character-level coders are needed to encode a huffman tree, for example.

For this project, we have implemented a wide variety of both word-level and character-level coders in the spirit of experimentation. They all differ in their compression efficiency, speed, and memory usage. Some are more optimized for a certain type of text data than others, but usually at the cost of pulling suboptimal numbers in other kinds of data.

The following two sections will briefly describe their pros and cons.

Character-Level Coders

Naive (static, 0-order)

parameters: none

This is a direct ASCII coder. It writes out every character as its 8-bit ASCII code. Although this is useless for compressing data, we used it to cleanly measure the effectiveness of performing a word-level compression since the dictionary of word types (serialized by a word-level coder) is not compressed.

using Huffman at the word-level with a Naive character-level coder

name	size (bytes)	compressed
anne	586969	230988
musk	1344739	446312
world95	2988578	995928

Considering the speediness of the coder, the result is spectacular.

TrainedHuffman (static, 0-order)

parameters: static unigram ASCII distribution

Given an estimated ASCII distribution, TrainedHuffman assigns optimal 0-order codes from a huffman tree. Because this is a static coder, it doesn't need to serialize itself to the compressed file. It works well because unigram ASCII distributions tend not to change drastically across English texts.

Note that the ASCII distribution must be learned directly from the output of the targeted serialization function rather than from a text file directly. Serialization process tends to insert control many characters like '\0', which must be accounted for. Otherwise, a frequent null terminator which appears in a serialized stream but not in a text file would be assigned a horrible coding. I learned this mistake after seeing a "compressed" larger than its original size.

AdaptiveHuffman (adaptive, 0-order)

parameters: initial unigram ASCII distribution, UPDATE_THRESHOLD

A problem with TrainedHuffman is that it does not handle abnormal ASCII distributions gracefully, although such a situation happens rarely. One solution is to use an adaptive coder that, as the name implies, adapts its model of the ASCII distribution as it encodes. AdaptiveHuffman uses a huffman tree to assign optimal 0-order codes given its most up-to-date distribution.

Unfortunately, implementing an adaptive huffman tree is somewhat complicated, so we approximate the adapation effect by reconstructing the tree after processing a block of UPDATE_THRESHOLD characters. Because the reconstruction process involves a non-trivial amount of computation, UPDATE_THRESHOLD=1 is costly. Instead, we set it to 1000, assuming that a distribution doesn't swing wildly within a small block of text.

AdaptiveHuffman encodes slightly efficiently than Huffman, but is slower.

TrainedBigram (static, 1st-order)

parameters: static bigram ASCII distributions

In English text, the probability of a character appearing next is most definitely not independent from the characters before it.

p(w1,w2,...,wn) = p(w1)p(w2|w1)...p(wn|wn-1,...w1) (n-gram)
p(w1,w2,...,wn) = p(w1)p(w2)...p(wn) Naive Bayes Assumption (unigram)

Representing a full n-gram model is obviously unfeasible as the size of the tables grow exponentially in n. However, we can approximate a large portion of the information contained in a n-gram model with a bigram model. For example, a bigram model captures the fact that a vowel is likely followed by a consonant, and vice versa.

p(w1,w2,...,wn) = p(w1)p(w2|w1)...p(wn|wn-1)

To reduce memory consumption and take advantage of English text, TrainedBigram only conditions on the English alphabets and numerals, and uses its unigram model for all other characters. This reduces the number of ASCII distributions from 257 to 26+26+10+1=63.

Even with a static bigram distribution, TrainedBigram works remarkedly well, especially in coding the word type dictionary of the word stream where most characters are English alphabets and digits.

TrainedArithmetic (static, 0-order)

parameters: static unigram ASCII distribution

This character-level coder uses arithmetic coding which in theory is more optimal than huffman coding in compression efficiency especiallly with highly skewed distributions. However, because ASCII distribution of English text is not highly skewed, the advantage of using arithmetic coding goes away.

Due to the nature of the algorithm, arithmetic coding is extremely slow in decoding. Without offering any advantages, TrainedArithmetic is largely unused.

Lempel-Ziv (LZ) (adaptive, k-order)

parameters: none

This encoder uses the LZW encoding scheme to compress a character stream. Instead of just using a fixed-length integer of a single size to encode the characters, we extended the encoder to incrementally increase the size of the fixed length integer encoding as the number of elements in the dictionary increased.

Because the LZW encoder uses repetition to encode longer and longer strings with a fixed length integer, the LZW encoder does well when there is a significant amount of repetition at the character level. Thus it is not surprising that the LZW encoder does well on encoding the separator stream, where there is expected to be few different characters and a lot of repetition.

Word-Level Coders

Huffman (semi-static, 0-order)

parameters: character-level coder, enumeration of tokens of the text

This word-level coder scans through the entire stream once to build a term-frequency dictionary, and assigns an optimal 0-order code to each term. Since the term-frequency dictionary information, or huffman tree to be specific, must be known by the corresponding word-level decoder, it is serialized to the compressed file. The serialization uses the provided character-level coder.

According to lecture notes, the number of word types grows as the square root of the number of tokens. This means the in memory huffman tree takes up O(n^0.5) space where n is the length of the document to be compressed.

Because Huffman does not make use of word ordering information, it can't compress frequently occuring phrases. However, due to the sheer size of the word-level symbol set (i.e: the set of word types), the compression gain by taking advantage of ordering information is much less pronounced than dealing with character-level symbol set.

This coder is fast and gives good compression result. The downsides are moderate memory usage, and it requires an extra pass to build the semi-static huffman tree.

AdaptiveHuffman (adaptive, 0-order)

parameters: character-level coder

Like its character-level counter part, AdaptiveHuffman behaves like the above Huffman word-level coder, except it adapts its symbol distribution on the fly. A major complication with any adaptive word-level coder is the uncertainty of the symbol set because the set of word types in English is infinite in size. If we were to scan the document first to build the symbol set, then we might as well use Huffman which assigns optimal codings.

AdaptiveHuffman solves this problem by building the term-frequency dictionary on the fly. For each block of the stream, it scans for new words and serialized them to the compressed file. For each word token coded, it perturbs the distribution. It rebuilds the huffman tree after processing each block of word tokens.

The main advantage of AdaptiveHuffman over Huffman is it doesn't require an initial pass over the file. Thus, it's able to deal with encode streaming data. Unfortunately, it's not nearly as efficient in compression as Huffman, so its applicability is narrow.

EnglishHuffman (semi-static, 0-order)

parameters: character-level coder, English codebook, enumeration of tokens of the text

One problem with the word-level Huffman coder is that the serialized huffman tree can be substantial. For example:

size of a serialized huffman tree (in bytes)

original file size	2988578
raw serialized huffman tree	232912
compressed file size	874400
compressed serialized huffman tree	115272

Although an appropriate character-level coder can compress the raw serialized huffman tree quite well (over 50%), it doesn't exploit the English language enough. Common words like "the", "to", and "of" will certainly appear in all text documents, and it's a waste to encode them in the same way as we encode less common words like "wolves".

EnglishHuffman uses an English "codebook" to help encode the top-most common terms. The size of the codebook determines the length of the codes, so while a large codebook will cover more word types, it uses more bits per coding. Experiments indicated that a codebook of size=2^16=65536 entries works well, and achieves a hit rate of over 70% on average. Words that are not defined in the codebook are encoded explicitly with the provided character-level coder.

EnglishHuffman is our best word-level coder for the word stream of data.

comparing Huffman and EnglishHuffman (in bytes)

compressed serialized Huffman tree	115272
compressed serialized EnglishHuffman tree	102516

Arithmetic (semi-static, 0-order)

parameters: character-level coder, enumeration of tokens of the text

The word-level Arithmetic coder is much more interesting than its character-level counterpart. For a symbol-set distribution that is highly skewed, such as the separator stream where " " typically appears over 75% of time, Huffman becomes suboptimal because it can't assign a "fraction bit". Arithmetic coder does it in an ingenious way.

This coder is our best word-level coder for the separator stream, but its decoding speed is excruciating slow.

TrainedEncoder1/2(semi-static, 0-order)

parameters: character-level coder, enumeration of tokens of the text

The idea behind a TrainedEncoder is to use a data-independent dictionary in order to encode words whenver possible. The advantage of using a pre-compiled dictionary is that the dictionary does not have to serialize itself. However, when writing out word encodings extra space must be used in order to indicate whether or not the the pre-compiled dictionary was used.

It turned out that the extra cost in indicating which dictionary to use was greater than the savings of not serializing the dictionary for the two different schemes that we tried.

Results

To interpret the results more conveniently, we will use the following notation to signify which coders are chosen to compress the separator and word streams.

sep = Huffman(LZ)
word = EnglishHuffman(TrainedBigram)

In this example, the separator stream uses the word-level Huffman with the character-level LZ coders, while the word stream uses word-level EnglishHuffman with character-level TrainedBigram coders. Unless indicated otherwise, this particular configuration was used to generate result data.

Comparing with gzip and bzip2

So as you can see, our compression engine always beats gzip by quite a significant margin, at times by over 10% of the original file size. bzip2 is tough to beat , but our compression engine eventually beats bzip2 as the size of the input file increases. We consider this quite an accomplishment given that our engine does not do the Wheeler-Burrows Transform.

gzip and bzip2 results

file	size (bytes)	our result	gzip 1.2.4	bzip2 1.0.1
anne	586969	0.3014	0.3795	0.2776
musk	1344739	0.2733	0.3646	0.2600
world95	2988578	0.2881	0.2922	0.1931
newswire	6534225	0.3010	0.3937	0.2863
g161	14729083	0.2684	0.3821	0.2747
mtent	59004086	0.2765	0.3894	0.2902

Experimenting with Different Coders

Interesting Configurations

• sep = Arithmetic(LZ)
  word = EnglishHuffman(TrainedBigram)
  This configuration offers the best compression ratios when tested using our test data. Use this if you want the absolute best compression regardlessly of time.

  file	ratio	bit/char
  anne	0.3014	2.41
  musk	0.2733	2.19
  world95	0.2881	2.31

• sep = Huffman(LZ)
  word = EnglishHuffman(TrainedBigram)
  (default configuration)
  This configuration offers a compression ratio almost as competitive as the above, but is much faster especially in decoding. This setting strikes a good balance among performance, speed, and memory usage, and this is why it was chosen as our "main" config. It's perfectly suitable for practical usage.

  file	ratio	bit/char
  anne	0.3065	2.45
  musk	0.2774	2.22
  world95	0.2883	2.31

Graphs and Tables

In order to label the graphs (without cluttering the graph too much), we had to abbreviate each configurations into a 4-tuple:

4-tuple = (word-level separator stream encoder,
character-level separator stream encoder,
word-level word stream encoder,
character-level word stream encoder).

Below is a table giving the mapping between integers and encoders.

0	Naive Character-Level
1	Trained Huffman Character-Level
2	Adaptive Huffman Character-Level
3	Trained Bigram Character-Level
4	Trained Arithmetic Character-Level
5	Lempel-Ziv (LZ) Character-Level
6	Huffman Word-Level
7	Arithmetic Word-Level
8	Adaptive Huffman Word-Level
9	English Huffman Word-Level
10	Trained Huffman #1 Word-Level
11	Trained Huffman #2 Word-Level

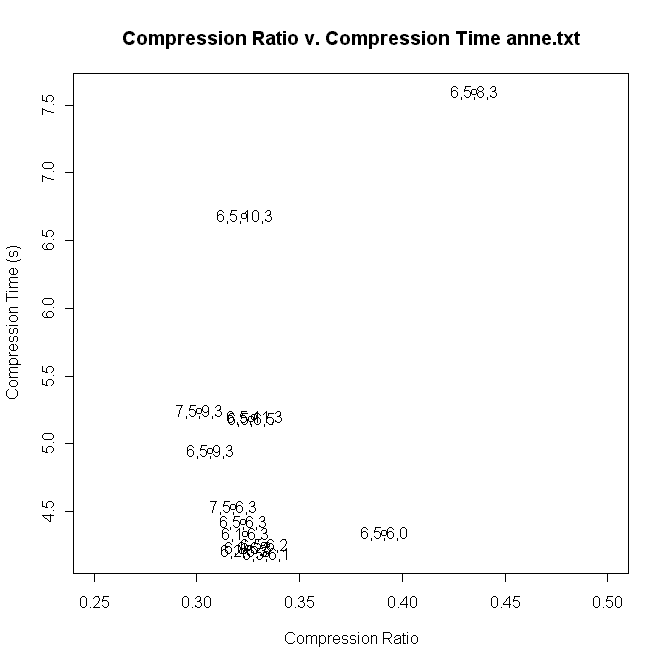
A scatter graph of the compression ratio v. the compression time for the file anne.txt. In general, methods that perform well should be to the lower left of the graph, and poorer methods to the upper right. Each point is labeled by the 4-tuple that indicates the encoders used to compress anne.txt. Our 'straw-man' for comparison is the (6,5,6,0), which uses a naive character-level encoder.


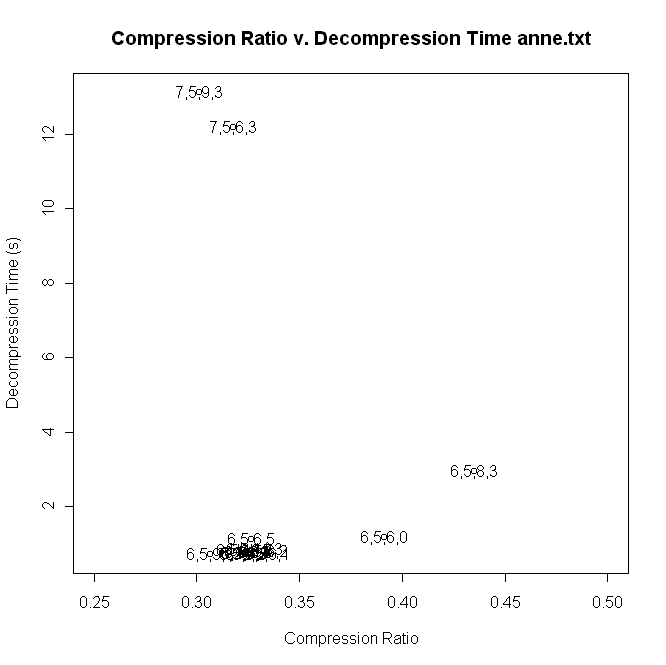
A scatter graph of the compression ratio v. the decompression time for the file anne.txt. (7,5,9,3) and (6,5,9,3) are the best performers in terms of compression ratio, but (6,5,9,3) has a big advantage in decompression time. You can see that the Arithmetic word-level encoder (7,x,x,x) is very expensive in terms of the decompression time costs.

More compression ratio vs time scatter graphs:

ratio vs time compressing musk
ratio vs time decompressing musk
ratio vs time compressing world
ratio vs time decompression world

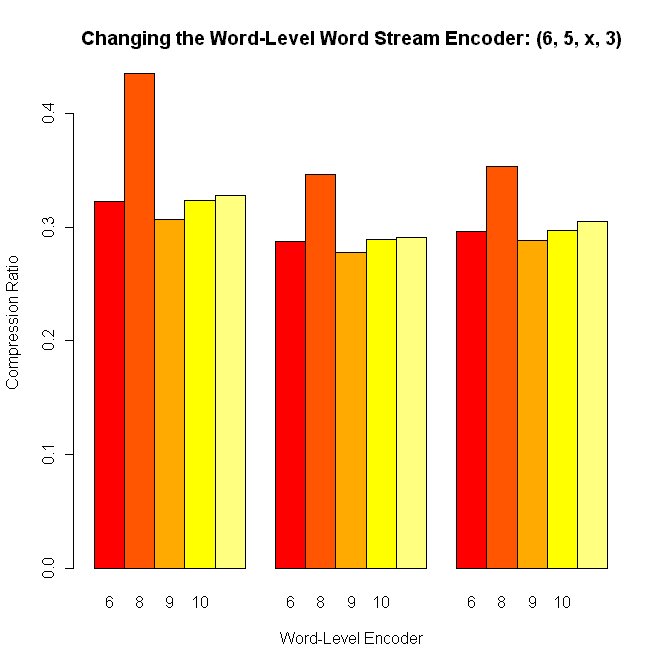
This type of graph compares the effect of varying one type of encoder on the compression ratio. Here, the label (6,5,x,3) indicates that the word-level separator stream encoder, the character-level separator stream encoder, and the character-level word stream encoder are all kept constant while the word-level word stream encoder is varied. The three sets of bar graphs represent the compression of three different test files (anne, musk, world95). It is clear from the graphs that the English Huffman Word-Level encoder performs the best, while the Adaptive Huffman Word-Level encoder performs the worst. One thing to note is that for graphs of this kind some combinations may not be shown simply because certain types of encoders do not work with other types.

More inter-coder comparison graphs:

Changing the Character-Level Word Stream Encoder: (6,5,6,x)
Changing the Word-Level Separator Stream Encoder: (x,5,6,3)
Changing the Character-Level Separator Stream Encoder: (6,x,6,3)

Analysis of Failed Models

Normalization by Stemming

Originally, instead of two streams - separator and word - we had a third stream to store stemmed suffixes. We used a modified Porter stemmer to decompose a word token into [canonical] [suffix]. The basic intuition was normalizing word tokens should decreases the size of the main dictionary substantially.

It turned out that most word tokens, over 90% on average, have empty strings as their suffixes. Therefore in the majority of the time, normalization by stemming actually performs slightly worse because some bits are needed to represent all those empty strings. Even the mighty Arithmetic coder was unable to amend the shortcomings.

one particular configuration with suffix stream enabled

file	ratio
anne	0.3187
musk	0.2840
world95	0.2925

the same configuration with suffix stream disabled

file	ratio
anne	0.3183
musk	0.2839
world95	0.2924

The degradation in compression efficiency isn't significant, but it must rely on the slow Arithmetic coder. Since this model didn't offer any advantage, we concluded that normalization by stemming does not aid compression.

Normalization by Decapitalization

Similar to above, we tried normalize a capitalized word token by converting it to lower case (note: we don't touch tokens like aBC or USA in order to preserve lossless compression).

one particular configuration with capitalization normalization

file	ratio
anne	0.3882
musk	0.3462
world95	0.3443

the same configuration without capitalization normalization

file	ratio
anne	0.3737
musk	0.3311
world95	0.3315

Using one bit to denote capitalization status, the normalization actually worsens compression efficiency. The percentage of capitalized tokens, below 10%, is tiny compared to the percentage of non-capitalized tokens. Such a skewed distribution calls for an Arithmetic coder (or run-length coding). But even so, performance did not improve. We had to conclude that normalization by decapitalization also does not help text compression.

Conclusion

Our attempt to achieve superior compression by specializing in English language text was fairly successful. While we were able to beat bzip2 on large enough files, we were better by at most a percent. It seems like the ratio of our compression ratio to bzips compression ratio would be likely to decrease even more on larger files.

We were surprised by the fact that stemmed data were not more compressible than the unstemmed data--however this may be because other forms of stemming may have been better--for example lemmatization.

While we chose to compare our compression application to bzip2 and gzip, it is worth mentioning that there are compression tools out there that can compress English text better than bzip2--with the caveat that they take a very long time.