Course Notes: Idempotent Productions
AbstractThis document provides an introduction to the concepts, methods and technologies covered in this course. The research and engineering disciplines spanned by this introduction are evolving so fast that by this time next year much of the content will be obsolete. Why would anyone bother to learn this material? The answer is that the ideas explored in this course will transform how we think about machine intelligence and make possible the next generation of smart systems. This class will prepare students to contribute to the development of this technology and help shape the way it is employed in society1.
Contents
1 Artificial Neural Networks & Machine Learning
1.1 Basic Terminology
1.2 Network Components
1.3 Vectors and Matrices
1.4 Activation Functions
1.5 Perceptron Models
1.6 Connection Matrices
1.7 Differentiable Models
1.8 Learning the Weights
1.9 Convolutional Layers
1.10 Multilayer Networks
1.11 Energy Landscapes
1.12 Accelerating Returns
1.13 Recurrent Networks
1.14 Signifying Meaning
1.15 The History of Ideas
1.16 Key Ideas Summary
2 Accelerated Evolution of Artificial Intelligence
2.1 Technology Predictions
2.2 Thinking About Thinking
2.3 Programmer's Apprentice
2.4 Memory and Computation
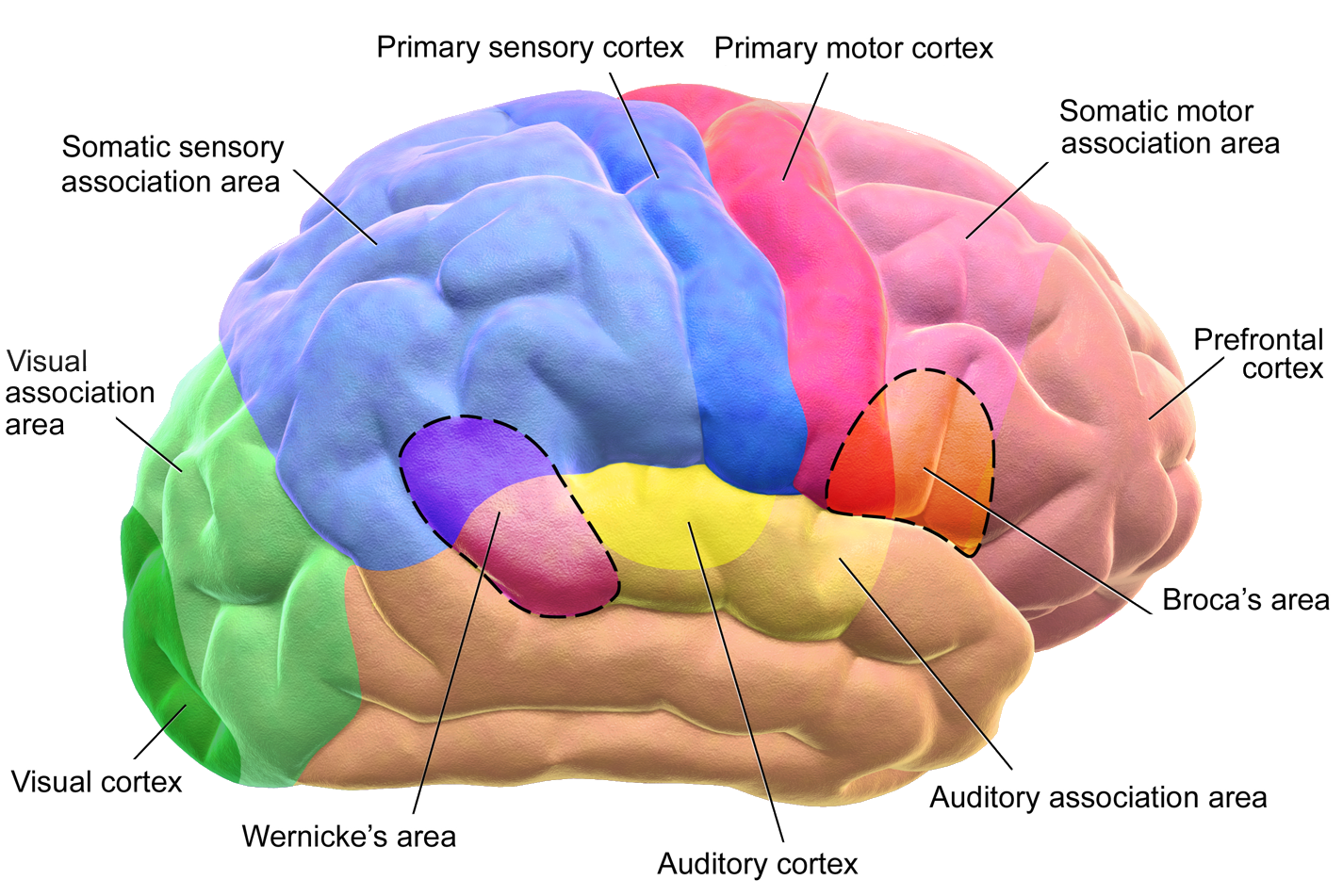
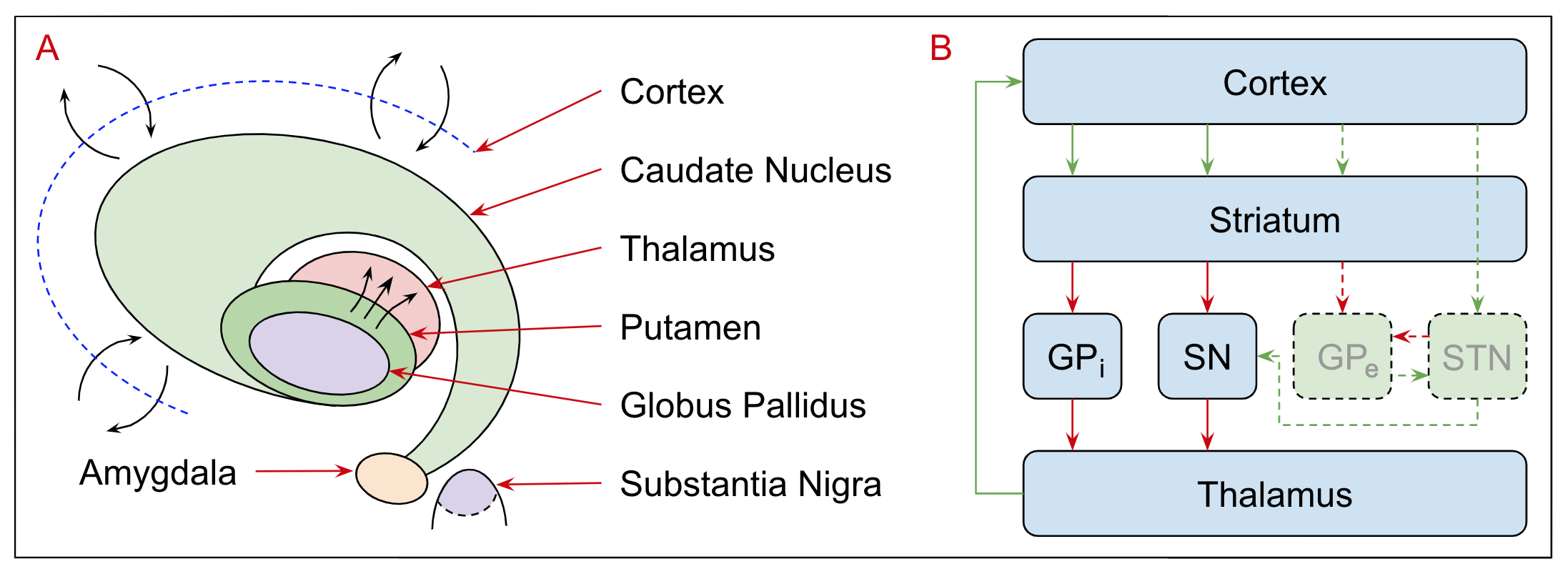
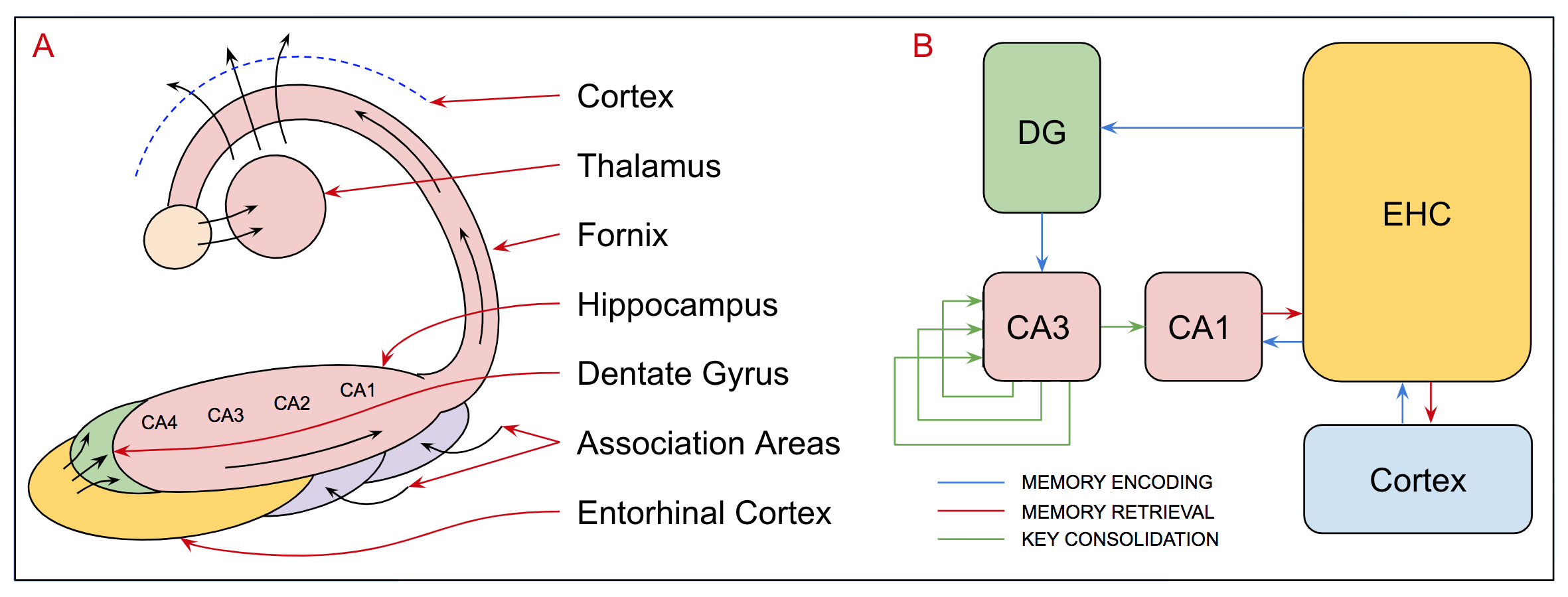
2.5 Cognitive Neuroscience
2.6 Anatomy and Physiology
2.7 Models of Human Memory
2.8 Neural Net Terminology
2.9 Reinforcement Learning
2.10 Attentional Networks
2.11 Machine Memory Models
2.12 Embodied Cognition
2.13 Planning and Behaving
2.14 Language and Thinking
2.15 The History of Ideas
2.16 Key Ideas Summary
1 Artificial Neural Networks & Machine Learning
This chapter describes the basic the machine learning and artificial neural network concepts assumed in this class. The class encourages multi-disciplinary teams working on final projects that combine expertise in computer science and neuroscience and so it is not necessary that everyone taking the class has mastered these concepts; however, familiarity with the basic ideas is strongly encouraged, since the concepts presented here will provide a foundation for understanding and applying the more advanced concepts covered in the next chapter.
The human brain is incredibly complicated. The more we learn about it, the more we appreciate the intricacy of its structure and the breadth of its function. Scientists think of it as a network of neurons, but it is so much more complicated than any engineer's model or artist's conception of a neural network as to beggar the imagination. There are hundreds of specialized cell types classified as neurons that employ a bewildering array of chemical, electrical, mechanical and genetic signaling pathways in order to communicate with one another2. Hardly a month goes by when there isn't some new experimental finding published in a respected journal that unsettles the prevailing dogma or calls into question some cherished theory3. As an example with profound consequences for how we comprehend and treat brain disorders, there are thought to be as many or more glial cells as there are neurons in the mammalian brain and we've only begun to understand their function — it is not, as was once believed and is still taught in some textbooks, simply a means of structural and housekeeping support for and insulation between neurons4.
Artificial neural networks (ANNs) are simple by comparison. The sort of ANNs now an integral part of machine learning were originally inspired by biological networks and continue to exploit new insights from neuroscience, but they are now rapidly evolving as researchers incorporate ideas from computer science and machine learning to improve their performance and reliability. Artificial neural networks provide interesting abstractions useful in studying the computational properties of brains — they were originally conceived for this purpose, but provide little to advance our clinical or scientific understanding of healthy and diseased brains. There is, however, a level of abstraction on which they largely agree, and it is this level of abstraction that has played such an important role in the success of so-called deep neural networks in outperforming humans on tasks once thought to be out of reach for AI technology.
We take a closer look at biological brains in subsequent chapters, but, for the remainder of this chapter, we focus on ANNs, including a nuts-and-bolts introduction to ANN technology to demonstrate just how simple are the basic components, and set the stage for an explanation of how we can assemble these components into powerful architectures that combine ideas from biological and conventional computing. I promise that this is the only chapter in which you will see an equation and there are only a few included here. The objective is to convey to you in as direct a way possible just how simple are the bones of this technology in order to give you a better idea of how neural networks can be compactly described, functionally extended, scaled and adapted to run on commodity desktop computers, commercial cloud computing services, phones and laptops and specialized parallel processing hardware.
1.1 Basic Terminology
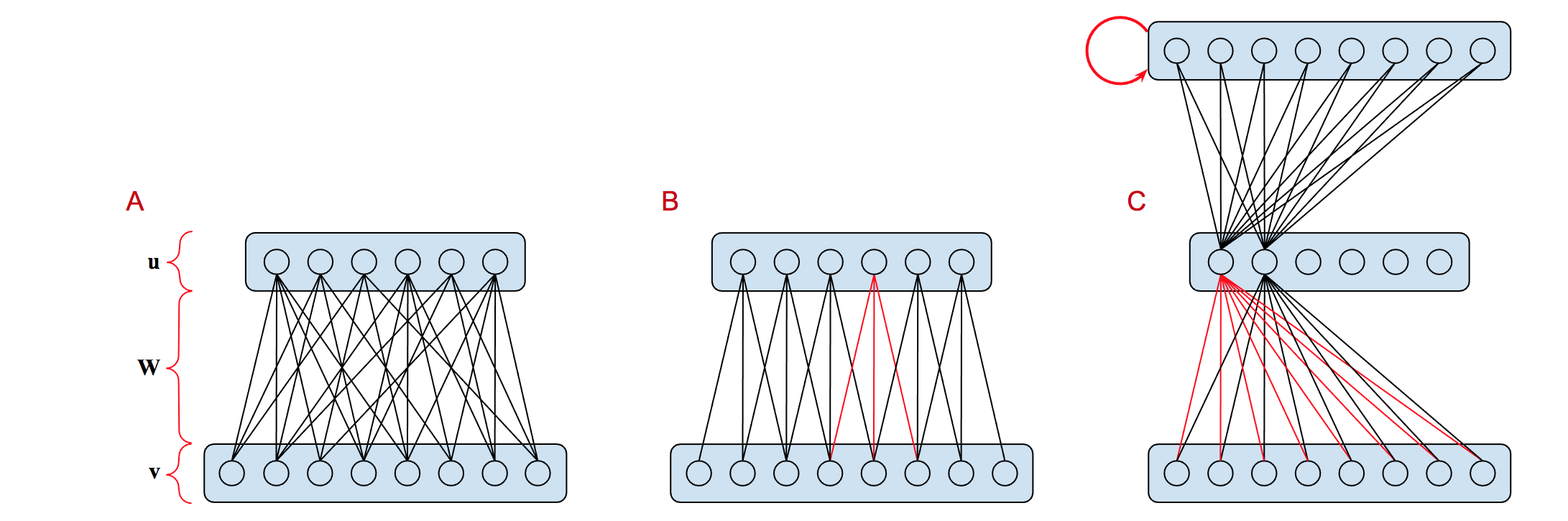
The terminology surrounding artificial neural networks can be confusing to the uninitiated. Part of the confusion arises due to the seemingly inconsistent uses of the word "layer". The network shown in Figure 1.A is characterized in the text as a single-layer perceptron5, whereas the network shown in Figure 1.C is called a multilayer perceptron6. The term deep neural network7 entered the lexicon much later and is generally used to refer to any artificial neural network with multiple layers between the input and output layer. We only briefly mention single-layer perceptrons in this chapter in order to make the point that these neural networks are less powerful8 than multilayer networks9 in a specific technical sense that sheds light on what it means to learn.
1.2 Network Components
In the following, we describe classes of specialized neural networks that can be used like Lego bricks to build more complicated architectures. We start by looking at three basic artificial neural network components. These three components are illustrated in Figure 1 and are examples of Lego-brick-like networks that can be used to construct more complicated networks. Networks are built of layers that are depicted as rectangular boxes with rounded corners.
| |
| Figure 1: Three of the most basic neural networks: (A) a single-layer perceptron has no hidden layers, (B) one layer of a convolutional neural network (CNN) showing one filter with a receptive field spanning three units, and (C) a multilayer perceptron (MLP) with one hidden layer and a recurrent (RNN) output layer. Note that a CNN layer used for object recognition might have 100 or more filters requiring that we replicate the network shown here once for each filter thereby creating a layer with a depth equal to the number of filters that feeds into a pooling layer combining the output of all the filters. Since there are six units in the output layer, if there were 100 filters instead of just the one shown, the resulting output layer would be \({6 \times{} 100}\) and since the parameters are shared and the receptive field — and hence filter size — is \({1 \times{} 3}\) there would only be \({3 \times{} 100}\) connection weights to learn. The MLP network is intended to show a connection matrix corresponding to a complete bipartite graph though only two units are shown to avoid an overly cluttered graphic obscuring the pattern of connections. The hidden layer of the MLP has fewer units than the either the input or the output layers which are of the same size, and so the hidden layer could serve as a bottleneck that facilitates learning a compact representation of the input, making (C) well suited to implementing an autoencoder trained by unsupervised learning. Finally, note that the output layer of of (C) has a recurrent connection highlighted in red here. The basic MLP architecture does not require recurrent connections. It is included here simply to underscore the fact that recurrent networks are just non-recurrent networks to which we have added one or more recurrent connections. | |
|
|
A neural network has two or more layers, an input layer, an output layer and zero or more hidden layers. Layers are stacked to construct networks. Each layer is composed of one or more units and selected units in one layer can be linked to selected units in an adjacent layer by connections. The units in adjacent layers and the connections between them constitute a graph in the terminology of graph theory where units are referred to as nodes in the graph and the connections between them are called edges. Graph theory10 is a sub-discipline of discrete mathematics, and won't figure prominently in our discussion except to characterize different patterns of connectivity. Nodes and edges have been associated with neurons and synapses in biological networks but the analogy can be misleading and is generally discouraged here and elsewhere in the scientific literature.
As a simple example of how graph theory is applied to neural networks, the connections plus the combined units in the two layers define a directed bipartite graph in which connections correspond to the edges in the graph and the units to nodes11. If each unit in the input layer — say there are \({n}\) of them — is connected to every unit in the output layer — say there are \({m}\) of them, then the connections form a complete bipartite graph and there are n × m connections — a number that can become rather large in practice. In our discussion of convolutional neural networks, we consider a powerful technique that ameliorates some of the computational problems that arise from working with very large input or output layers.
1.3 Vectors and Matrices
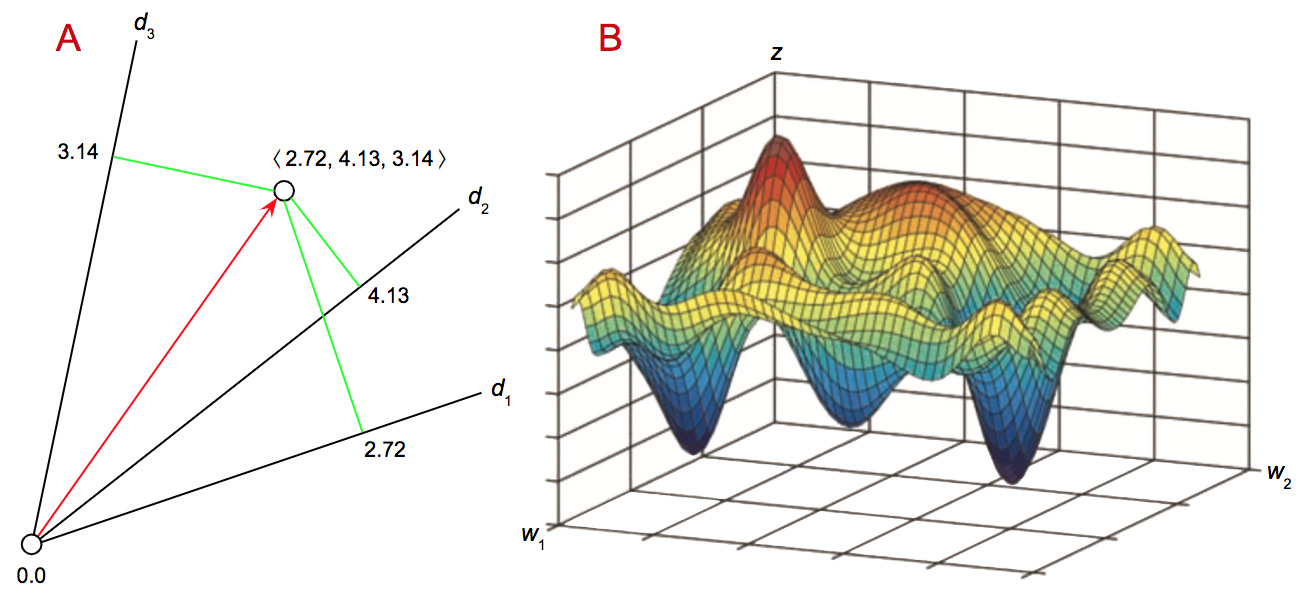
Neural networks represent both mathematical and computational objects. The nodes in a layer correspond to variables in equations describing the mathematical functions that neural networks implement as computable objects. It is often appropriate to think of the variables within a layer as defining vectors in a vector space and the edges as defining linear transformations from one vector space to another12. A vector space is an \({n}\)-dimensional generalization of the familiar three-dimensional Euclidean space you might have encountered in high-school calculus. A vector represents the coordinates of a point in that space — see Figure 4.A. This abstraction frees us from having to deal with individual units in layers and allows us to bring to bear the full power and beauty of linear algebra13 and multivariate calculus14 in order to share models and exploit powerful software packages and specialized hardware to expedite engineering and accelerate the computations required to develop, train and deploy neural networks in various applications.
From this perspective, each layer represents a sequence — ordered list — of variables that can be used to assign numeric values to the units that comprise a layer. This sequence is called a vector in algebraic matrix theory which is the underlying branch of mathematics associated with neural networks. A vector variable represents a sequence of scalar variables — meaning that each variable corresponds to single real number15, often referred to as vector components each of which can be assigned a numeric value. We display vector variables in bold font and scalar variables in italics using subscripts to refer to the individual units in a layer / components in the vector. For example, the expression \({\mathbf{u} = \langle{}u_1, u_2, \ldots, u_n\rangle{}}\) defines \({\mathbf{u}}\) to be a vector variable consisting of \({n}\) components shown as subscripted scalar variables delimited by angle brackets. A neural network defines a mathematical function that takes as input a vector of real numbers and produces as output a second vector of real numbers. The term function is used loosely to apply to both the abstract mathematical object and to any computable instantiation of that object corresponding to a program that runs on a conventional computer or specialized hardware designed specifically for neural networks.
In specifying functions represented by a network we often iterate over all the components in a vector using an indexed variable \({u_i}\) as in the expression \({\sum_{i-1}^{n} = u_1 + u_2 + \cdots+ u_n}\) representing the sum of the components of the vector \({\mathbf{u}}\). Algebraic matrix theory allows us to add two vectors component wise as in \({\langle{}1.3, 4.0, 7.5\rangle{} \oplus\langle{}0.5, 1.9, 5.2\rangle{} = \langle{}1.8, 5.9, 12.7\rangle{}}\) or normalize a vector \({\mathbf{u} = \langle{}4.0, 1.0, 5.0\rangle{}}\) by dividing each component by the sum of all the components as in the equation, \({\mathbf{u}\,/\,\sum_{i-1}^{i} u_i}\), which in this case yields the vector \({\langle{}0.4, 0.1, 0.5\rangle{}}\) in which all of the components are between \({0}\) and \({1}\) and together sum to \({1.0}\). Note that this calculation involves three scalar divisions, \({(4.0\,/\,10.0)}\), \({(1.0\,/\,10.0)}\) and \({(5.0\,/\,10.0)}\). These operations can be carried out in parallel given a processor such as the graphics processing unit (GPU) found in most laptops and cell phones.
1.4 Activation Functions
In the sequel, we define our neural network building blocks as having two or more layers where the required two correspond to the input and output layers. Where it aids exposition, we depict the individual units within layers and draw the connections between the units in adjacent layers. Otherwise, to render the diagrams less busy graphically, we hide the individual units using just the iconic round-edged rectangles as a visual proxy for the corresponding vectors and draw a single edge between the two layers to represent the linear transformation between the relevant vector spaces. Each layer is also characterized by an activation function — typically nonlinear — that is described in the text but generally not graphically depicted in the network architecture diagrams.
The artificial neural networks discussed here are said to be discrete-time16 rather than continuous-time dynamical systems17. The state of an artificial neural network at any point in time corresponds to the values assigned to the variables that constitute the vectors associated with each layer. For our purposes, each tick of the clock corresponds to a pass through the entire network during which all of the variables in the network are updated. Conceptually, it is easiest to think of the input layer as being on the bottom of a stack of layers culminating in the output layer at the top of the stack. A forward pass starts at the bottom with an assignment to the input layer, computing each layer in turn and ending up at the top with the final assignment to the output layer, ignoring for now the details of how we handle recurrent connections.
When we speak of a single layer \({L}\) as one of many in a stack of layers, think of the input to \({L}\) as being the vector of variables corresponding to all of the units that connect to the units in \({L}\). The update for a specified layer \({L}\) at time \({t}\) is defined as follows: given assignments to the variables in the input to \({L}\) at \({t}\), compute the linear transformation associated with \({L}\) and pass the result to the activation function associated with \({L}\) to obtain the assigments to the vector of variables associated with output of \({L}\) at \({t}\). The corresponding vector of values associated with the output of \({L}\) at time \({t}\) is called its activation state. The technical term thought vector is also used to refer to the activation state of a layer, but we generally reserve the term for hidden layers and, in particular, hidden layers that encode abstract concepts — though admittedly the meaning of the word "abstract" in this setting is a bit murky.
While we discourage equating patterns of spiking neurons in biological networks with the activation states of hidden layers, we will draw upon work in cognitive and systems neuroscience to make the case that both representations are examples of highly-parallel distributed codes capable of representing the sort of context sensitivity that one expects from connectionist systems [93]. Such representations are in stark contrast with the systematic, combinatorial nature of largely-serial symbolic systems that account for traditional computing paradigms such as those based on the computer architectures of Alan Turing [15] and John von Neumann [87]. There are also significant differences in that biological networks are continuous-time while most current artificial networks are discrete time.
Biological networks are inherently subject to the problems described by von Neumann in his treatise on the synthesis of reliable machines, including living organisms, from unreliable components [132], whereas artificial neural networks run on hardware that finesses the problems that von Neumann alludes to by enforcing the digital abstraction [37]18. If the spiking activity of biological neurons is primarily in service to achieving some degree of stability in the behavior of such neurons — whether by managing the cell's metabolic equilibrium to maintain internal state or by employing some method of coding19 to enable the reliable transfer of digital signals between neurons, then perhaps biological neurons enforce their own digital abstraction.
1.5 Perceptron Models
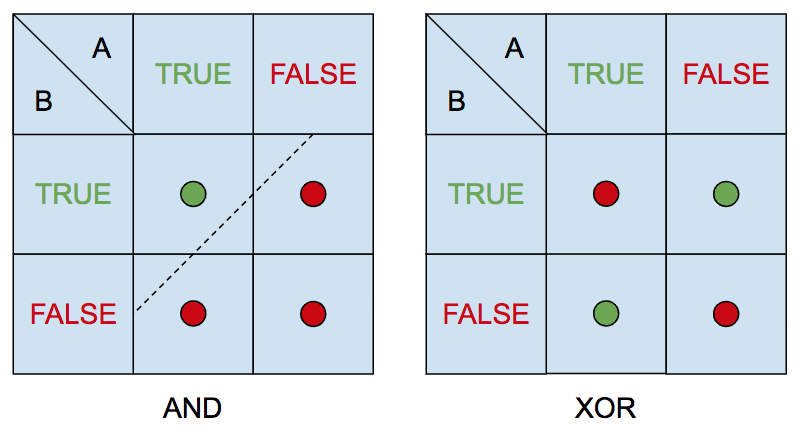
Layers sandwiched between the input and output layers are called hidden layers and play a key role in learning. Figure 1.A shows an historically important network called a perceptron or, more specifically, a single-layer perceptron20. A single-layer perceptron has no hidden layers and is restricted in what it can learn to the set of binary classifiers said to be linearly separable and perhaps best understood by an example21.
| |
| Figure 2: The binary AND function (representing the conjunction of two Boolean variables) is linearly separable and so it is easy to learn a classifier defining a straight line that divides the four possible Boolean assignments into two classes with a single-layer perceptron22. The XOR function (representing the exclusive disjunction of two Boolean variables) is not linearly separable since there is no single straight line (one-dimensional hyperplane) that divides the four assignments into two classes and hence XOR is not learnable with a single-layer perceptron. For each binary function, we show a simple two-dimensional space and plot each of the four possible truth assignments using a green circle to indicate assignments such that the respective binary function is TRUE and a red circle to indicate assignments for which it is FALSE. We show a linear separator for the AND function and it should be obvious by inspection that no such separator exists for the XOR function. A multilayer perceptron (MLP) with at least one hidden layer can learn any binary classifier including one that correctly classifies XOR. | |
|
|
The Boolean function for conjunction denoted AND is defined as follow: for any Boolean propositions \({A}\) and \({B}\), if \({A}\) and \({B}\) are both true, then the expression \({A}\) AND \({B}\) is true and otherwise, i.e., for any other assignments of truth values to propositions, it is false. Perceptrons have no problem learning the AND function. The Boolean function for exclusive disjunction denoted XOR is defined as follows: if \({A}\) is true and \({B}\) is false or \({B}\) is true and \({A}\) is false, then \({A}\) XOR \({B}\) is true, and otherwise it is false. Figure 2 illustrates how the property of linear separability distinguishes these two functions.
1.6 Connection Matrices
While the values of the units in a layer are determined by the input and the function defined by the network and connection weights, the connection weights are initially assigned randomly and then learned from data to complete the definition of the network function. The connection weights for a given layer are represented by a mathematical object called a matrix23. that stores the weights in a tabular format so that the row indices refer to the units in the bottom layer and the column indices refer to the units in the top layer. A matrix with \({n}\) rows and \({m}\) columns is called an \({n \times{} m}\) or \({n}\)-by-\({m}\) matrix where \({n}\) and \({m}\) are referred to as the dimensions of the matrix.
By convention, a matrix is generally denoted by an upper case letter in bold font, e.g., \({\mathbf{W}}\), and the individual matrix components are displayed in italics as done with vector components, except that they have two indices, e.g., \({w_{i,j}}\), one index to reference the row (\({i}\)) and the other to reference the column (\({j}\)) in which the entry is stored as illustrated below: $${\mathbf{W} = \begin{pmatrix} w_{1,1} & w_{1,2} & \cdots& w_{1,m} \\ w_{2,1} & w_{2,2} & \cdots& w_{2,m} \\ \vdots& \vdots& \ddots& \vdots\\ w_{n,1} & w_{n,2} & \cdots& w_{n,m} \\ \end{pmatrix} }$$ Matrices and vectors are related in that a \({1 \times{} n}\) matrix is called a row vector and a \({n \times{} 1}\) matrix is called a column vector.
The function definition corresponding to the perceptron network shown in Figure 1 can be written concisely as the equation \({\mathbf{v} \mathbf{W} = \mathbf{u}}\) where \({\mathbf{v} \mathbf{W}}\) denotes the matrix multiplication of \({\mathbf{v}}\) and \({\mathbf{W}}\) that determines the output vector \({\mathbf{u} = \langle{}u_1, u_2, \ldots{}, u_m\rangle{}}\) such that \({u_{i} = v_{i}w_{1,i} + \cdots{} + v_{i}w_{n,i} = \sum_{j=1}^{n} v_{i}w_{j,i}}\) for \({i = 1,\ldots{}m}\). Such compact notation considerably simplifies both describing neural networks and writing programs that implement neural networks since there exist programming languages that allow the same succinct representation thereby freeing the programmer from having to read and write the low-level code that implements operations on vectors and matrices.
1.7 Differentiable Models
As described so far, the function associated with a network is simply a linear transformation mapping from one vector space to another24. Moreover, since the composition of two linear transformations is itself a linear transformation, any neural network consisting of a stack of such layers defines a linear transformation. This means that, if you are trying to learn a nonlinear function — and much of what we want to learn is nonlinear, the best you can hope for is to find a linear function that closely approximates the nonlinear one. Of course, it could be that a good linear approximation does not exist. For this reason, we apply a nonlinear activation function to the result of performing the linear transformation, thereby enabling the network to learn nonlinear functions as well.
Learning inevitably involves search. In the case of learning a model corresponding to an artificial neural network, it involves searching in the high-dimensional space of possible assignments to the connection weights. Each weight assignment corresponds to a fully instantiated network function, and the learning algorithm is restricted to find a model within the space of all such functions. This restriction is referred to as an inductive bias25 in learning theory and it plays an important role in guiding search to predict outputs, given inputs that it hasn't encountered in the training data. Bias in the context of machine learning is a good thing since without bias there can be no generalization. The selection of activation functions and network topologies also serves to define the set of possible network functions and further bias the search. Here we consider two of the most common activation functions.
It is often handy to have a binary switch or threshold function. Whenever you have to make a choice between two options, e.g., between two competing chess moves or whether a photo includes a cat, you are making a binary decision. For example, the threshold function, \({f : \mathbf{R} \mapsto{} \{0,1\}}\), defined: if \({x \geq{} 0}\) then \({f(x) = 1}\) otherwise \({f(x) = 0}\), maps a scalar value on the real number line to the Boolean values \({0}\) or \({1}\). We can also use this scalar function to implement a component-wise vector version, \({\mathbf{f} : \mathbf{R}^m \mapsto{} \{0,1\}^m}\), defined: \({\mathbf{f}(\mathbf{v}) = \langle{}f(u_1), f(u_2), \ldots{}, f(u_m)\rangle{}}\). Another useful function is the max function \({f : \mathbf{R}^m \mapsto{} \mathbf{R}}\), defined: \({f(\langle{}u_1, u_2, \ldots{}, u_m\rangle{}) = u_i}\) such that for all \({j\,\neq{}\, i, u_j \leq{}u_i}\).
The problem is that these functions are discontinuous and hence they are not differentiable26. The threshold function has a discontinuity at \({0}\) — or its vector equivalent \({\mathbf{0}}\) in the case of the vector function, and the max function is also discontinuous though the multivariate case is a bit trickier to explain27.
To get around this problem, we substitute the continuous sigmoid and softmax functions for, respectively, the discontinuous threshold and max functions. These two continuous activation functions are among the most common such functions used in the design of artificial neural networks. A scalar sigmoid function, \({L : \mathbf{R} \mapsto{} \mathbf{R}}\), can be implemented in terms of the logistic function28 as: $${L(x) = \frac{1}{1+e^{-x}} = \frac{e^{x}}{e^{x}+1}}$$ where \({e}\) is the natural logarithm base — also known as Euler's constant \({2.71828 \ldots{}\,}\), and the most common corresponding vector function is the obvious component-wise \({\mathbf{L} : \mathbf{R}^{K} \mapsto{} \mathbf{R}^{K}}\). The softmax function, \({\mathbf{S} : \mathbf{R}^{K} \mapsto{} \mathbf{R}^{K}}\) is defined as a generalization of the logistic function: $${{\mathbf{S}}({\langle{} u_{1},\,\ldots{},\,u_{K} \rangle{}) = \langle{} z_{1},\,\ldots{},\,z_{K} \rangle{} {\rm{\;such\;that\;}} {z_j = \frac{e^{z_{j}}}{\sum_{k=1}^{n}e^{z_{k}}}} {\rm{\;for\;all\;}} k = 1 \ldots{} K}}$$ that squashes and normalizes a \({K}\)-dimensional vector \({\mathbf{u}}\) of arbitrary real values to a \({K}\)-dimensional vector \({\mathbf{z}}\) of real values such that each entry, \({z_i {\rm{\;for\;all\;}} i = 1 \ldots{} K}\), is in the interval \({(0, 1)}\) and all the entries sum to \({1.0}\). In order to understand why it is important that the objective function be differentiable, we need to consider how neural networks are trained.
1.8 Learning the Weights
Once the architecture of the network is completely configured — including the number of units in each layer, the connections between layers and the activation function for each layer, the only step remaining to fully define the network function is to assign values to the connection weights. This is referred to as training a neural network and, as mentioned earlier, it involves searching in the high-dimensional space of possible assignments to the connection weights. One of the most powerful algorithms for training neural networks is called stochastic gradient descent29. While it is possible to train a large network by breaking it up into more tractable pieces and training each piece separately, this is generally undesirable since it often means optimizing the pieces in isolation resulting in a global solution that is suboptimal. Training the entire network simultaneously is called end-to-end training30.
Training relies on an objective function — also called a loss function — to evaluate the expected performance of the network for a given assignment of connection weights and guide search for an optimal assignment31. SGD attempts to minimize the network loss by following the gradient which is the multi-variate generalization32 of the derivative — the derivative for a real-valued function \({f(x) = y}\) measures the sensitivity to change of the output value \({y}\) with respect to a change in its input value \({x}\) and plays an important role in machine learning by way of the calculus of variations33.
Developing an artificial neural network that can be trained end-to-end with gradient descent involves the design of a differentiable objective function. This can be challenging given that many of the supporting functions routinely used in defining objective functions for related optimization problems are not differentiable. These basic support functions include the threshold and max functions mentioned earlier Since the objective function incorporates the network function, we can't compute the gradient of the objective-function and apply SGD unless the network function is differentiable, and if the network function uses the discontinuous threshold function mentioned earlier then the network function will not be differentiable. When used to minimize the above function, the standard34 gradient descent method performs the following weight update on each iteration: $${\mathbf{w}_{t+1}\,\colon{=}\,\mathbf{w}_t -\eta{} \nabla{} L(\mathbf{w}_t)}$$ where \({\mathbf{w}_t}\) is the vector of all the weights in the network prior to the update, \({L}\) is the objective or "loss" function, \({\eta{}}\) is the learning rate that determines how much to change the weights on each iteration, \({\nabla{}}\) is the gradient operator and \({\nabla{} L(\mathbf{w}_{t})}\) is the gradient of the loss, and \({\mathbf{w}_{t+1}}\) is the updated vector of all the weights.
1.9 Convolutional Layers
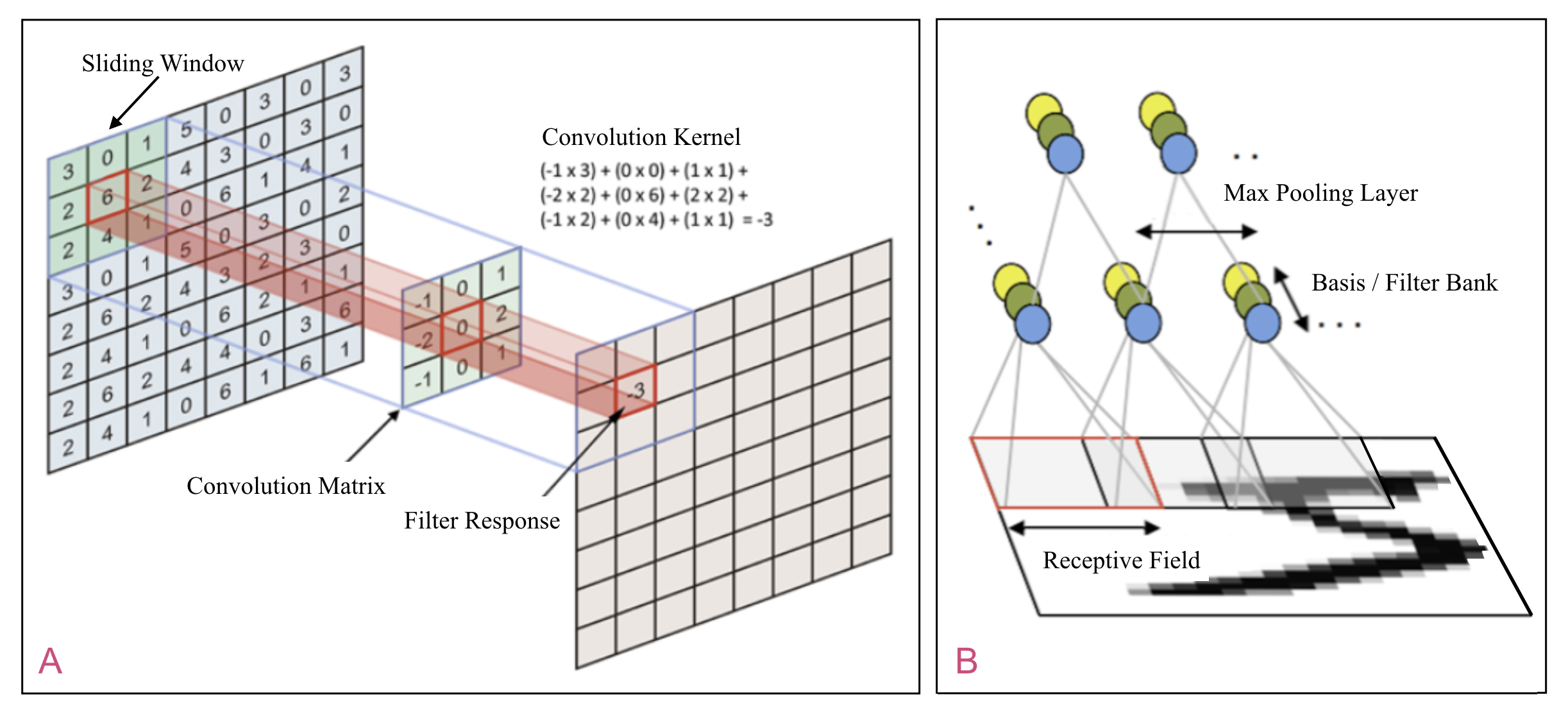
Fully connected neural network layers don't scale well to large inputs such as high-resolution images. If we have an input vector corresponding to a million pixel image, e.g., \({1000 \times{} 1000}\), and an output vector of the same size, then the fully connected weight matrix for the resulting bipartite graph would have a trillion (\({10^{12}}\)) entries. The class of models called convolutional neural networks (CNNs) solve this problem by recoding large input layers as the composition of features that span relatively small contiguous regions of the input35. In the case of an image, these features might correspond to small patches that represent abrupt changes in contrast — often called edge detectors — and thereby emphasize the boundaries of objects.
In the terminology of CNNs, such a feature is called a filter — specifically a linear filter36, and the contiguous region to which it applies is its receptive field. A collection of filters is called a filter bank, and a typical filter bank could easily include hundreds of filters, e.g., a set of edge detectors that discriminate edge orientation in increments of \({5^{\circ}}\). A fully configured convolutional layer consists of a set of slices, one slice for each filter in the filter bank. Figure 1.B represents a single CNN slice and the connections highlighted in red depict a \({1 \times{} 3}\) filter consisting of just three weights. Let \({\mathbf{v} = \langle{}v_1, v_2, v_3, v_4, v_5, v_6, v_7, v_8\rangle{}}\) represent the vector corresponding to the input layer and \({\mathbf{u} = \langle{}u_1, u_2, u_3, u_4, u_5, u_6\rangle{}}\) represent the vector corresponding to the slice output layer.
The filter as shown has a receptive field corresponding to \({\langle{}v_4, v_5, v_6\rangle{}}\) and is poised to compute the response of the filter at \({u_4}\) in the output layer of the slice. The response value is intended to measure how well the filter accounts for the part of the image covered by its receptive field. If you think of the filter and the receptive field as vectors — if they happen to be some other shape, e.g., a 2-D array as in the case of images, then just flatten them to make a vector, then one of the most common methods is to use cosine similarity37 as a proxy for the angle between the two vectors. In the case of vectors in positive space, i.e., all of the vector components are positive, cosine similarity is bounded by \({1.0}\) for an angle of \({0^{\circ}}\) — so the two vectors are parallel and hence similar — and \({0.0}\) for an angle of \({\pi}\) radians — the two vectors are perpendicular and hence dissimilar.
Often the inner — or "dot" — product of two vectors is used as a more easily computed but numerically less stable measure of similarity that must treated with mathematical care. If the filter vector is \({\mathbf{w} = \langle{}w_1, w_2, w_3\rangle{}}\) and the receptive field vector is \({\mathbf{u} = \langle{}u_4, u_5, u_6\rangle{}}\) then the response value at unit \({v_4}\) in the output layer of the slice is the dot product of filter weight vector and the receptive field input vector \({\mathbf{w} \cdot{} \mathbf{u} = (w_1 * v_4) + (w_2 * v_5) + (w_3 * v_6)}\). The filter response is computed for each unit in the output layer of the slice. This is done for all slices and the slices are stacked in column vectors such that the \({i}\)th element of this vector corresponds to the computed response of the \({i}\)th filter. If we started with a square — two-dimensional — matrix of pixel values we would now have a three-dimensional output layer. The activation function for this layer is typically max pooling38 in which the output of pooling collapses the extra dimension added in order accommodate the filter responses by selecting the maximum value in each column vector.
Note that if we have a bank of 100 \({10 \times{} 10}\) filters, each slice has 100 weights and there is a total of one thousand weights for the entire filter bank. That's quite a difference from the trillion weights required for the fully connected case. The downside of this saving is that we can only learn relatively small features. However, if we stack convolutional layers — as is typically done in practice — we can learn a hierarchy of features that account for increasingly larger patterns in the image at each successive stage in the hierarchy.
Convolutional networks are not biologically plausible in the particular way that they share variables and compute filter responses. They are, however, extraordinarily powerful neural network components and have shown off their advantages in diverse applications far from computer vision including natural language processing. Moreover the required computations can be efficiently carried out on parallel processing hardware such as are used in rendering graphics39.
1.10 Multilayer Networks
Figure 1.C depicts a multilayer perceptron — commonly called a deep neural network — with one hidden layer. The MLP network is intended to illustrate a connection matrix corresponding to a complete bipartite graph though only two units are shown to avoid an overly cluttered graphic obscuring the pattern of connections. The output layer of (C) has a recurrent connection highlighted in red, making the point that a recurrent network is just a non-recurrent network with recurrent connections. In the case shown here, we might update the output layer by taking the average of the current activity with that of previous, e.g., \({\mathbf{v}_{t} = ( \mathbf{v'}_{t} + \mathbf{v}_{t-1} )\,/\,2}\) where \({\mathbf{v'}_{t}}\) is intended to represent the layer output prior to taking the recurrent connection into account.
In the example shown here, the hidden layer of the MLP has fewer units than either the input or the output layers which are of the same size. This is not required in general and only serves in the present circumstances to demonstrate a special case of MLP called an autoencoder that is worth emphasizing here40. An autoencoder is an MLP that facilitates learning a compact encoding of the input that reconstructs the input and in so doing assists generalization — the ability to generalize from the training data to account for novel input. For this reason, the resulting encoding is often referred to as a generative model. The narrowing in the hidden layer is sometimes referred to as a bottleneck in that it prevents training from simply learning the identity function41.
Generative learning is contrasted with discriminative learning in that the latter emphasizes discriminating between similar examples and needn't construct an explicit model of the data, whereas the latter emphasizes learning a general model that can be used for multiple purposes by downstream components in an MLP with many layers. An important feature of autoencoders is that they can be trained by unsupervised learning in which the objective function compares the original encoding represented by the input with the encoding produced by the learned model represented in the output layer and the objective function measures the fidelity of the reconstruction. More sophisticated objectives penalize reconstruction error while at the same time rewarding the facilitation of downstream components.
While we seldom learn models just for the sake of learning them, in some cases, a discriminative model is just what you need, as in the case where you want to sort manufactured parts into two categories: defective versus certified. Generative models are often useful in cases in which their ultimate purpose is not known or clearly understood, or when it is important to explain why the system made a decision or arrived at a particular conclusion. There is some evidence to suggest that humans employ some form of Bayesian statistical inference42 to construct generative models of their environment that explain how humans can make reliable generalizations from so little data — what are commonly referred to as inductive leaps in learning.
1.11 Energy Landscapes
The notion of an energy landscape43 arises in many disciplines where optimizing a function is seen as search in a combinatorial space of possible parameter settings of a complex system. In the case of computational chemistry, the parameter settings correspond to the possible conformations of a molecular entity and the goal is to find a conformation that minimizes the free energy of the system44 so that we can build a model of molecular structure to use in synthesizing new materials or drug discovery [133, 74]. In the case of training an artificial neural network, our goal is to search for a weight assignment (conformation) that minimizes the loss function (free energy).
| |
| Figure 4: The left (A) graphic shows the coordinate axes of a three dimensional vector space — also known as a Hilbert space45 — along with a single vector \({\langle{}2.72, 4.13, 3.14\rangle{}}\). Such vectors are used to represent the activation states of artificial neural circuits encoded in the numerical assignments to the units in a ANN layer. We associate a distance metric — typically the obvious generalization of the Euclidean metric — with the vector space that allows us to compute the distance between two vectors as a measure of their similarity. The graphic on the right (B) represents an energy landscape which is a map of all the possible conformations of a complex system and their corresponding energy levels. The conformations of a neural network correspond to the set of all possible weight assignments and the energy levels correspond to the value of the loss function for each such assignment. Here we show a very simple example with just two weights — \({w_1}\) and \({w_2}\) — and the loss plotted on the \({z}\) axis to create the continuous surface of the energy landscape. The goal of training a neural network is to find a global minimum of the loss function using stochastic gradient descent to search in weight space by crawling around on the energy landscape. | |
|
|
Figure 4.(B) illustrates the energy landscape for a network consisting of two weights, \({w_1}\) and \({w_2}\), assigned to what are conventionally called the \({x}\) and \({y}\) axes, and the value of the objective function on the \({z}\) axis computed at each point on the \({x\,y}\) plane. The resulting rugged surface exhibits multiple local maxima and minima. Ideally the surface would be convex but this is rarely the case in practice46. In training networks with millions of weights, the energy surface is likely to be pockmarked with local minima as well as saddle points47 that can mislead gradient descent. More sophisticated methods using second-order partial derivatives can test if a critical point is a local maximum, local minimum or saddle point, but they don't scale and can't be expected to point the way to global minimum of the objective function. Remarkably, in many cases, having more parameters results in a rougher landscape — more potholes to get stuck in, but also produces more local minima that are closer to the global minimum. Suffice it to say that a great deal of effort has been put into designing better solvers.
1.12 Accelerating Returns
Researchers developing neural network solutions typically have to train and test hundreds if not thousands of experimental networks. It's one thing if running a test on a network, takes no more time than it takes to grab coffee, and quite another if it takes days or even weeks. It helps if you're working in industry and have access to unlimited computing resources. Unfortunately, there is no such thing as unlimited computing and engineers are always competing with one another and with the needs of customers to get their work done. It is perhaps no surprise then that engineers have taken to applying neural networks to automatically and efficiently search in the space of network architectures for solutions that satisfy their needs.
This kind of technology is part of a trend in applying machine learning technology recursively to accelerating the development machine learning technology. Throughout the last few decades, researchers working on neural networks often expressed frustration with progress in the development of better analytical tools, mathematical foundations, software and scalable infrastructure to run it on. At times, the state-of-the-art in developing neural-network technology seemed more like alchemy than science or engineering.
The wave of excitement around the beginning of the new millennium as neural networks were shown to outperform more traditional methods of machine learning was tempered by a realization that we were in uncharted territory. There was time when, miraculously and contrary to received wisdom, adding more layers or layers with more units and more connections often seemed to help rather than hinder finding good if not optimal solutions. Researcher puzzled over why this should happen, and the mathematically adept resurrected old or developed new sophisticated regularization methods to understand such phenomena48.
Neural network technology is flourishing in large part because it has been so successful and there are so many smart individuals contributing to its development and savvy companies investing in a growing ecosystem of talent and supporting technologies. Artificial neural networks have received the lions share of the attention but the dividends from its success are being spread across a much wider spectrum of technologies including robotics, computer vision, imaging, advanced biosensors and neural prostheses.
An entire generation is growing up with possibility of living decades longer than their parents, conquering the major causes of mental and physical decline and developing technology to make us smarter and better able to address problems on global scale. Machine learning, artificial intelligence, synthetic biology, genetic engineering and materials science are advancing at an incredible, some would say alarming pace, reinforcing and accelerating one another. It may sound trite to say so given all the hype surrounding these technologies, but we will have evolve along with our technologies if we are to continue to play our enhanced and artificially intelligent friends.
1.13 Recurrent Networks
In his book I Am a Strange Loop49 Douglas Hofstadter explores the idea of consciousness and the concept of "self" in terms of a recurrent process thereby dismissing the philosopher's confusion about homuncular regress50 and the viewer in the Cartesian theatre51. In a subsequent chapter, we consider how one might go about implementing a digital assistant that exhibits many if not all of the properties of human consciousness worth preserving in an artificial intelligence. The artificial neural network implementation makes use of recurrent connections to explain and provide a compelling use case for the emergent phenomena of inner speech52 and self-reflection. In the following, we explore more practical, less controversial applications of recurrent networks.
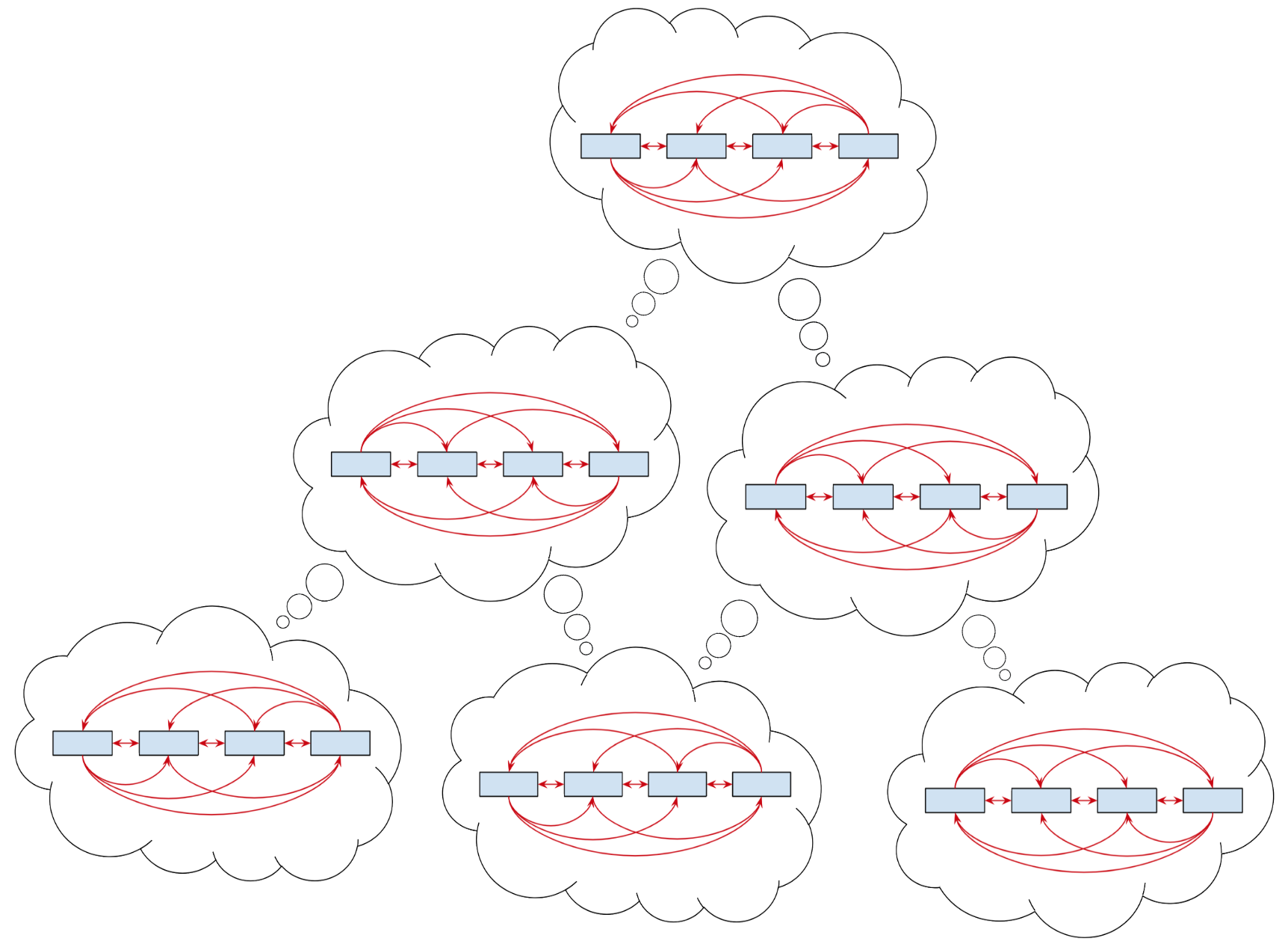
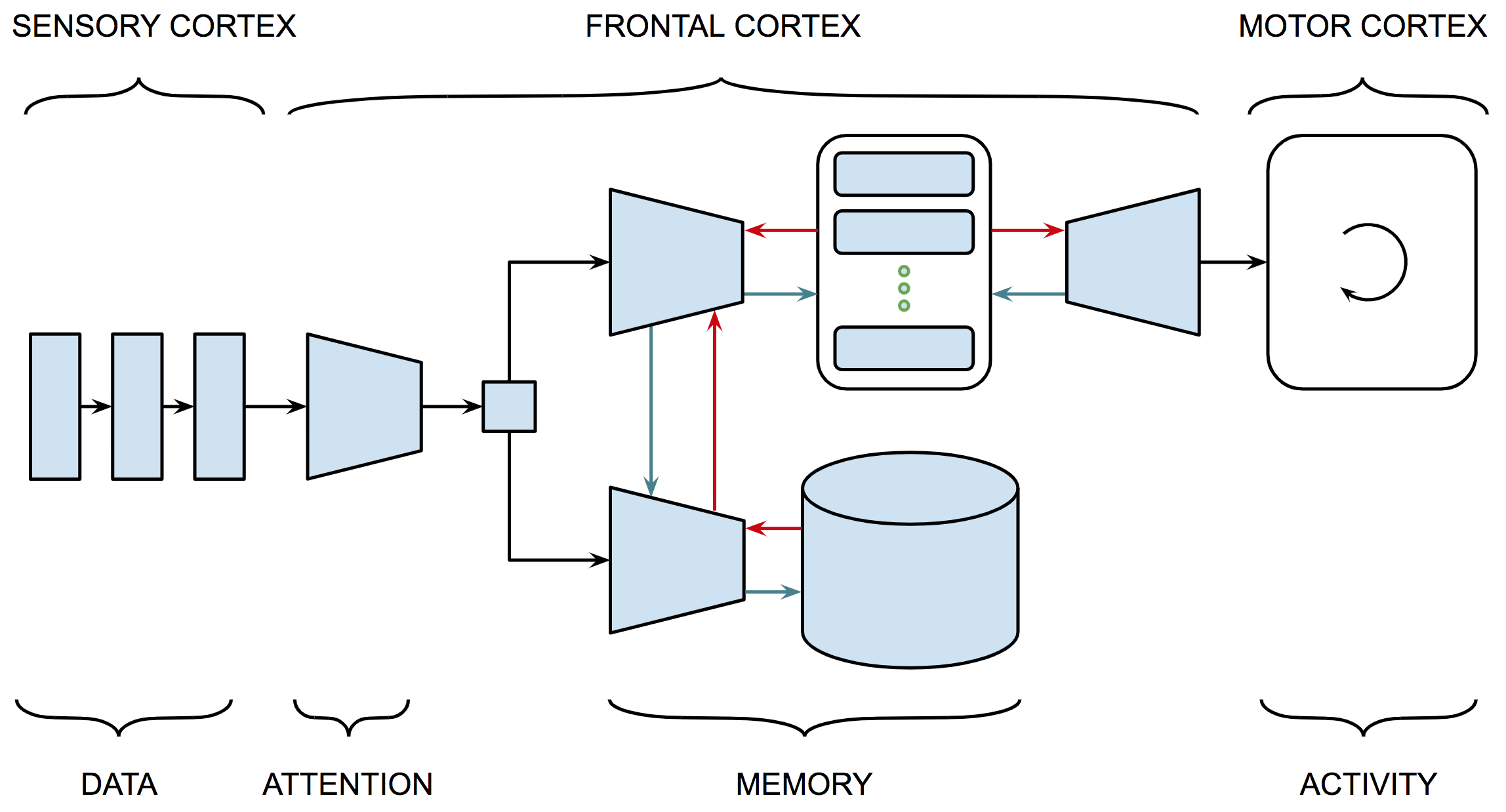
All three of the networks shown in Figure 5 are said to be recurrent. In contrast, the networks shown in Figures 1.A and 1.B include only feedforward connections. Recurrent connections run in the opposite direction from feedforward connections and can span multiple layers. A recurrent connection can also feed back into the same layer it originated from as illustrated in Figure 1.C or it can connect two units within a layer. Recurrent neural networks — networks that have recurrent connections — will play an important role in our understanding human cognition and figure prominently in our discussion of neural network architectures53.
Even the simplest biological networks make use of feedback. Without feedback, networks couldn't keep state — they couldn't remember past events, they couldn't measure progress or adjust their responses to deal with errors in perception or motor control. Norbert Wiener55 introduced the term cybernetics56 to describe the study of systems that employ feedback to control their behavior. Biological systems employ feedback to regulate everything from hormone balance to consciousness. The three networks shown in Figure 5 illustrate the use of feedback to support three basic functions: attention, memory and recursion. In subsequent chapters we'll apply these basic functions to support a wide range of activity. Here we take a closer look at how they are implemented since, the detail provide insight into how they work and how they might adapted for other purposes.
| |
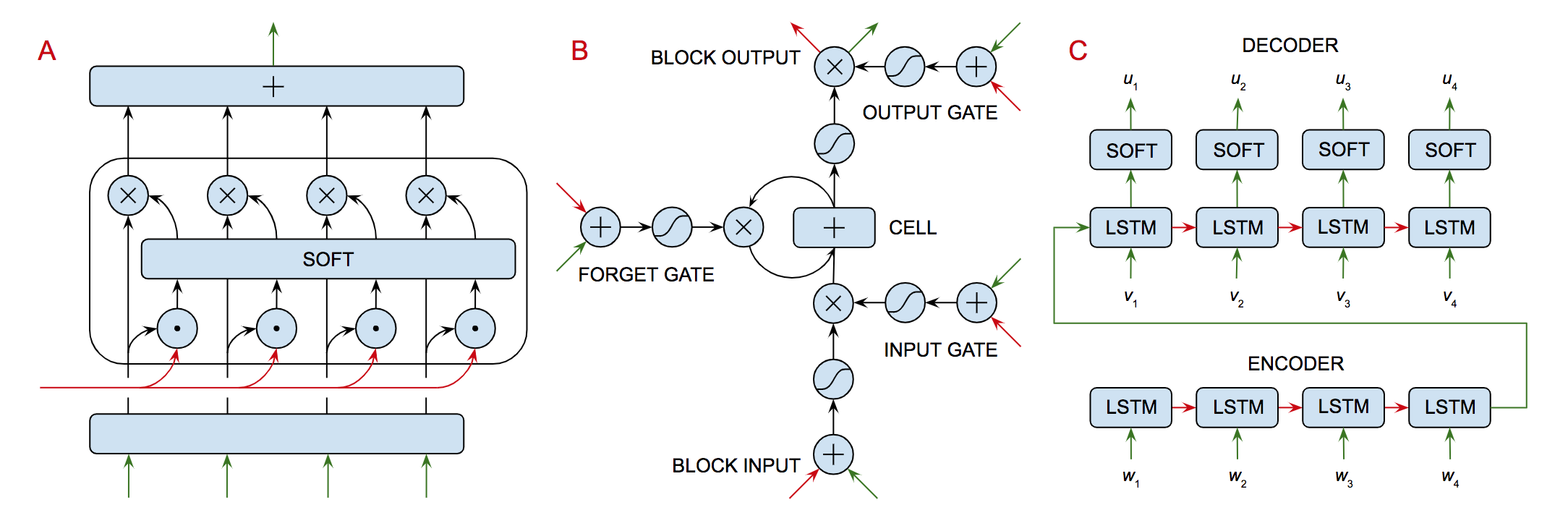
Figure 5: Three specialized neural networks components that deal with: (A) selective attention, (B) short-term memory, and (C) and working with structured data. To minimize clutter, the drawings don't show the individual units or their corresponding connections. Each directed edge represents a group of connections between the units in the corresponding adjacent layers and implements a linear transform as discussed earlier. We use the following conventions for representing activation functions:
| |
|
|
Three specialized recurrent neural networks components are illustrated in Figure 5: (A) is an attentional network that learns how to shape the context for performing inference as in the case of machine translation or continuous dialogue, (B) is a short-term memory module that learns how to anticipate information required for inference and set it aside until needed, and (C) is a network architecture consisting of a pair of recurrent networks used to transform one sequence into another as in the case of question answering.
Figure 5.A shows a schematic description of an attentional selection module that learns what part of our recent experience is most important for our current purposes and makes that information available to guide inference. The network shows four (feedforward) connections to the bottom layer each of which corresponds to a thought vector of the same size. The red (recurrent) connection corresponds to a single thought vector summarizing the current state of information, i.e., the context for current decision making. Each of the feedforward vectors is concatenated with the current context vector and fed into a softmax layer, the output of which is used to decide (gate) which of the four (feedforward) thought vectors is most relevant to the current context.
The attentional selection module is useful in machine translation (MT) to determine which parts of the original (input) sentence are relevant in deciding the next word in the translated (output) sentence. For example, in deciding the gender or number — singular or plural — of a pronoun to use in the translation it is often useful to refer back to any previous information in the input sentence that mentions the reference of the pronoun under consideration. The network in Figure 5.C is designed to support MT as well as other problems that involve transforming one sequence — of words in the case of MT — to another sequence.
Figure 5.B shows a schematic description of a gated memory module that can be used for any application in which it is useful to learn what information to keep in short-term memory in performing a task. This module makes use of three trainable gates that control the contents of a memory cell. The three gates determine (a) when the cell content should be updated with the current input, (b) when the current content of memory should be made available as output and (c) when the current content should be erased.
Each gate consists of a learnable network that takes as input both feedforward and feedback connections, computes the weighted sum of these inputs and then applies a sigmoid activation function to produce a (differentiable) approximation to a binary switch. The scalar output of the sigmoid function can be used to — depending on the gate — add the block input to the content of the memory cell, make the content of the memory cell available as the block output, or control whether the current content of the memory cell is fed back to cell by the gated recurrent connection or not, i.e., it is forgotten.
As an example, if the output value of the forget-gate sigmoid is close to one and the output value of the input-gate sigmoid is also close to one, but the output-gate sigmoid is close to zero, then the cell memory will contain the sum of its previous content and current block input vector and the block output will be (approximately) a vector of all zeros the same dimensionality as the memory cell content — which is the same size as input block vector. This affords the rest of network using the gated cell block a great deal of learnable control over the information required to perform its assigned duties.
The autoencoder described in Figure 1.C works well for learning useful representations of fixed size data like still images or video from a given camera58. In principle, you could make it work with text data in the form of sentences for machine translation or documents for summarization, but processing text sequentially is convenient for many applications including, for example, continuous conversation and sentiment analysis59. Recurrent models are particularly useful for such applications and there is a variation on the autoencoder architecture we described earlier that has proved especially versatile for working with structured data including but not limited to text sequences.
The Long Short-Term Memory (LSTM) model was invented by Sepp Hochreiter and Jürgen Schmidhuber [57]. It was originally developed to deal with a problem in training recurrent models in which the gradient either grows without bound or shrinks to zero. The initial version of an LSTM block included memory cells plus input and output gates as described in our discussion of Figure 1.B. Forget gates were added later by Felix Gers [45]. A fully configured LSTM includes one or more memory cell blocks along with conventional multilayer network components that control the memory cell gates in order to anticipate the need for and remember state information for as long as is required.
Figure 5.C shows the LSTM model used as the recurrent module in an encoder-decoder architecture that can be trained for machine translation, dialogue management or code synthesis. Unlike the stacked encoder-decoder architecture of the autoencoder, here we have a separate encoder and decoder each of which is implemented as a recurrent neural network. The encoder ingests the input sentence, \({\langle{}w_{1},w_{2},w_{3},w_{4}\rangle{}}\), one word at a time starting with some initial thought vector encoding previously processed text and providing a context for understanding the next sentence in a document or conversation.
When the sentence is completely ingested, the encoder hands off the resulting thought vector to the decoder that generates the translation, \({\langle{}u_{1},u_{2},u_{3},u_{4}\rangle{}}\), one word or phrase at a time. The decoder enriches the thought vector it has been provided as its input in order to account for its extension of the ongoing translation. The decoder continues in this fashion until the translation is complete. In Figure 5.C there is just one LSTM network for the encoder and one for the decoder. The graphic shows the recurrent process as it unfolds over time one word at a time. The lengths of the two sentences needn't be the same.
In production, the output of the decoder is sent to a softmax layer that generates a probability distribution over possible next words that is used to select the next word in the translation. Training data consists of source-language target-language sentence pairs, e.g., \({\langle{}\,\langle{}w_{1},w_{2},w_{3},w_{4}\rangle{},\,\langle{}v_{1},v_{2},v_{3},v_{4}\rangle{}\,\rangle{}}\). During training, the encoder-decoder is provided with such a pair and the objective function takes into account the difference between the supplied target, \({\langle{}v_{1},v_{2},v_{3},v_{4}\rangle{}}\), and the generated translation, \({\langle{}u_{1},u_{2},u_{3},u_{4}\rangle{}}\).
Knowing the exact technical details regarding how LSTM technology works is not our goal here. The LSTM technology is now nearly two decades old and several related competing technologies have been developed in the meantime. The important take away is that the LSTM technology provided us with new capabilities and did so by using existing components and relying on fully differentiable networks that can be trained with gradient descent. An LSTM can learn to anticipate information that it will need later, store that information and maintain it until it is required. The information is stored in the form of a high dimensional vector, what we have been calling the thought vector, that allows us to encode abstract concepts in a native format that is completely compatible with our existing neural network technology. We can further enhance these capabilities by incorporating the attentional module in Figure 5.C.
In subsequent chapters will look at network architectures that allow us to make complex predictions about the future and use those predictions to construct and execute plans to solve all sorts of practical problems from driving a car to writing a computer program. These architectures will depend upon the same basic components and training methods in much the same way that designing new computer architectures depends upon the same logic gates and memory devices as the computers we use today. Many of the recent innovations in the development of artificial neural networks have come about by figuring out better ways of training such networks that don't rely upon labeled data and that can be trained in stages by exposure to increasingly complicated learning environments much as a child learns by building new skills on top of existing ones throughout the decades long developmental stages that set humans apart from any other organism that we know about.
As we follow this thread throughout the subsequent chapters, we will also be looking for opportunities to accelerate skill acquisition by artificial means in both humans and machines. The path to Matrix style uploading of new skills is probably either technically infeasible or simply too risky to perform on humans anytime soon. But it may be possible to develop AI systems dedicated to the education of each individual child in a way that was never practical for either public school systems or working parents. The implications of this for society could herald new hope for a broadly educated, well informed self-governing society.
1.14 Signifying Meaning
Words are signs and signs signify meaning. According to Charles Sanders Peirce60, one of the founders of semiotics61, there are three types of sign: icons, indexes and symbols. Words are symbols. This turns out to be important in communicating ideas that have a precise technical meaning, but not so much for communicating about more fluid concepts.
What about images? Images are also signs and signify meaning. We know how to represent images in a computer. Images are composed of pixels arranged in rectangular grids and pixels are represented as numbers encoded as bit vectors. Unfortunately, this representation isn't particularly useful for working with visual information in artificial neural networks. Let's consider the meaning of images, and we'll get to words and the fact that words are symbols in due course.
The meaning of words and images is all about context62. If we're looking at a photo of a barnyard with cows and pigs and a farmer sitting on a tractor, and we notice something the size of a small dog wearing what looks like a red hat, we might reasonably jump to the conclusion that it's a rooster. However, if someone were to cut out and then present us with just the pixels corresponding to a pig or the farmer's upper torso, we probably wouldn't have clue what we were looking at.
From linguistic standpoint, individual words have little meaning without some context in which to interpret their meaning. In conversation, the context of a spoken word has many levels: the words that immediately proceed and follow, the last few statements, our previous conversations with the person we are speaking, etc. We rely on context to imbue words with meaning in developing neural networks to handle natural language. Here is a good example of how, by taking inspiration from human cognition in the design of neural network architectures, we achieve a high degree of competency. This observation is not surprising given that we invented natural language to serve our purposes.
We represent words, phrases and larger fragments of language by embedding63 them as points in high-dimensional vector spaces so that nearby points are semantically related and different dimensions reflect different comparative characteristics along which words differ such that relatively simple operations, e.g., subtracting one vector from another, expose these differences and reveal these relationships. In this approach, the boundaries between words are not sharply defined and meaning has a tendency to drift as usage evolves and exposure to language changes over time, e.g. you start reading more Tolstoy and Dostoyevsky and fewer superhero comics.
We can create embeddings of all sorts of abstract entities including relational graphs, computer programs, taxonomies, family trees, organizational charts, social networks, dynamical system models, etc. We can use such models to answer questions, "Who was Sophie's grandmother her father's side?, make predictions "What if the pressure relief valve failed?" and keep track of and reason about personal interactions "Does Alan know Sherry has the keys?". AI systems can't automatically decide when to learn these model but that is largely because the current generation of AI personal assistants aren't smart enough [...] humans do this sort of thing all the time. Creating models and making use of them is an integral part of how we [manage our complex lives | go about our every day lives | conduct business ].
1.15 The History of Ideas
The limitation to linearly-separable classifiers was considered so restrictive that it effectively discouraged a generation of computer scientists from pursuing research in this area. Academic advisers would often speak disparagingly about neural network, joking that the second best approach to solving any problem was either an artificial neural network or genetic algorithms — proponents of which were likened to alchemists in their single-mined pursuit of a method for turning dross into gold, thereby sending a clear signal to their students not to waste time pursuing such solutions.
A number of determined researchers persisted and were able to demonstrate that networks with one or more hidden layers were able to learn much more complicated functions. These networks — often referred to as multilayer perceptrons would resurface decades later as so-called deep neural networks. The reason for the delay can be attributed to several factors. Multilayer networks required more connections and hence more parameters; with more parameters to fit it was assumed that it would be easy to overfit, and, as a consequence, generalization and therefore performance on unseen data would suffer. There were also numerical problems with the existing optimization algorithms and surface of the energy landscape was riddled with potholes corresponding to local minima for gradient methods to fall into or saddle points where the slopes (derivatives) in orthogonal directions are all zero, but which is not a local extremum of the function64.
Among those who kept the faith a small group of researchers who referred to themselves as the PDP group were able to make considerable theoretical progress even without the benefit of more powerful computing resources. Some of the most prolific included David Rumelhart, Jay McClelland, Geoffrey Hinton, Terrence Sejnowski, David Touretzky and Peter Dayan. Hinton in particular developed a huge number of sophisticated models, useful algorithms and clever insights. Together they created a wealth of science and technology that would serve as a springboard when the tide turned in the late 20th and early 21st century and neural networks saw a reversal in fortune and a renaissance in the underlying theory and practical applications of neural networks.
It is perhaps worth pointing out that despite the contributions of the PDP group and those few stalwarts who followed in their footsteps, much of the opposition came from researchers in the United States who were convinced that symbolic methods and logic-based artificial intelligence was the best way to pursue AI. The 1980s saw the rise of expert systems and rule-based technologies promulgated by researchers at Stanford University including John McCarthy and Ed Feigenbaum. During the same time members of the PDP group and their colleagues in cognitive science were discovering how symbolic and connectionist approaches complemented one another, explaining how human beings solve complex problems.
During the 1980s and the decades following, interest in connectionist models remained relatively strong in Canada, Europe and Asia with Yoshua Bengio, Jürgen Schmidhuber and Kunihiko Fukushima among those making foundational contributions. During the same period, the PDP group produced a two-volume compilation of their research and that of their students and colleagues that consolidated their research and has provided a wonderful resource for the current generation of connectionists65.
The computational resources available to most researchers at the time were such that training was prohibitive or at the very least tedious — it is difficult to make progress when running one experiment takes days to complete with little or no intermediate indication that it will produce a good solution. In the intervening years the picture has changed dramatically. Increasingly personal computers and small servers were being networked and networking hardware was becoming faster even relatively small academic departments could afford to build clusters consisting cheap commodity computers.
Practical parallel computing was still in its infancy but as innovations in semiconductor lithography increased the number and density of transistors you could fit on an integrated circuits, chip manufacturers started designing chips with multiple cores and dedicating silicon to SIMD66 hardware (implementing so called single-instruction, multiple-data parallelism) and a few intrepid hackers were figuring out how to write parallel programs that ran on dedicated graphics processors [...] eventually better graphics, cell phone technology and the Internet would create an insatiable demand for computing resources [...] leading to the rapid deployment of cloud computing services and data warehouses sprinkled around the globe [...]
1.16 Key Ideas Summary
Here is a summary of the most important ideas covered in this chapter:
Networks with one or more hidden layers are more powerful than those with none;
Biological and artificial neural networks rely on different design principles;
ANNs exploit different opportunities for parallelism than biological networks;
Biological and artificial neural networks use similar computational strategies;
ANN vectors play a similar role to spiking neurons in biological networks;
Gradient descent relies on the network objective function being differentiable;
Convolutional neural networks work on large input layers by sharing weights;
An hierarchy of convolutional layers can learn features at multiple scales;
Autoencoders use unlabeled data to learn representations without supervision;
Recurrent networks extend feedforward networks using feedback to retain state67
Attentional networks learn how to create an appropriate context for inference;
Encoder-decoder architectures make it possible to work with structured data;
Nonlinear Functions
We make a rather big deal about linear systems in these pages. Linear functions are generally more tractable to manipulate mathematically. It's as if you were to draw a Venn diagram, linear functions would look like a small circle surrounded by everything else — meaning all the nonlinear functions. Like a tiny kernel in middle of a giant peach. Classifiers that have certain linear properties are easier to learn than those that don't. Linear systems are easier to control than nonlinear systems. Linear systems theory is pretty much a closed book — current textbooks look a lot like the textbooks that were printed 40 years ago.
Often complex systems include a combination of linear and nonlinear components simplifying analysis somewhat, but there is always the concern that the nonlinear parts are the most important understand68. I can't remember just now who first said it — might have been Carver Meade, but I seem to recall I heard it from Bruno Olshausen: "It isn't surprising that neurons behave nonlinearly. What's surprising is that in combination they can manage to behave linearly." John von Neumann's ideas concerning the synthesis of reliable organisms from unreliable components were motivated by dealing with unreliability of vacuum tube components for building computers, but apply equally well to biological systems.
One important consideration is that solving systems of linear equations can be done in polynomial time69. Linear systems theory70 is enormously useful in a wide range of applications from seismology to circuit design. Linear programming is often used to generate approximate answers to intractable problems. For example, many important optimization problems in operations research can be expressed as a (mixed) integer linear program71 which are notoriously hard to solve given that integer programming is NP-complete.
One of the easiest approximations is to reduce the problem to a linear program by relaxing the integral requirement, solve the resulting linear system and then round the original integer variables to satisfy the integral requirement72. This approximation runs in polynomial time and often produces solution that are competitive than those arrived at by (mixed) integer linear program solvers.
No Magic Required
I've said that this chapter is an attempt to make sure that you understand exactly what an artificial neural network consists of. If you follow the presentation here, you should be able to look at an artificial neural network and break it down into simpler components until everything can be written down as an equation and that equation consists entirely of basic arithmetic operations, including additions, subtractions, and multiplications plus a few mathematical functions such as sines and cosines that are either familiar to you from high school math or easy to understand intuitively when plotted as a graph.
I want you to contrast that level of understanding with our current understanding of biological neural networks composed of neurons. These are living cells that are constantly directing their genetic machinery to manufacture the molecules required not only to perform the complicated signaling that goes on when two neurons communicate with one another, but also produce the proteins and lipids that are required to maintain its molecular integrity and generate the energy required for every operation carried out in the cell. And then there are the poorly understood glia, the dark matter of the brain. We do know a lot about neurons but I would hazard a guess that (a) there is much more that we don't know than we do, and (b) we are not even sure that what we think we know is true.
Anybody who tells you that artificial neural networks are nothing like biological neural networks is very likely to be right, but their confidence is unwarranted since at best they dimly perceive the true function of biological networks. Simply because no one does. Moreover, there may very well be a strong case to be made that at some level of description artificial and biological networks are more similar functionally than they are different, and that there is a great deal of value to be had by studying artificial neural networks if you want to understand biological ones. Later we will talk about different levels of abstraction and the overused and often abused concept of emergence. At that point, I hope we can make even more clear the benefits of studying artificial networks.
2 Accelerated Evolution of Artificial Intelligence
In this chapter, we investigate the prospects for building digital assistants that meet or exceed human performance in specialized technical areas and are capable of interacting with humans using natural language to collaborate and share knowledge. We draw upon research from cognitive and systems neuroscience for insight into the neural basis of human cognitive function. The sections on automated planning and natural language processing are a work in progress and will be fleshed out with help from our invited speakers and the students taking the class.
2.1 Technology Predictions
In the previous chapter we looked at some of the basic neural-network components from which more complicated network architectures are constructed. These components, referred to as Lego-block like networks, are the foundation for the current generation of artificial neural networks. The intention is to make it clear that there is no magic and demonstrate that the basic ideas are accessible to anyone with high-school math. In this chapter, we use those basic building blocks to predict the next generation of personal assistants. This exercise sets the stage for thinking about how the technology might help us deal with the problems facing us as a species.
To focus discussion, we consider a personal assistant that works with a software engineer in the role of an apprentice learning on the job, as was common in the guilds and trade associations of medieval cities and continues to this day in some crafts such as glassworking, albeit with better laws to protect the rights of employees. The programmer's apprentice we consider here is a novice programmer but has the intuitive skills of an idiot savant, given that the apprentice has a suite of powerful programming tools as an integral part of its brain. The assistant application allows us to explore the important role of language in solving problems and the technical challenges in exploiting cognitive enhancements.
While the next generation of AI systems will include personal assistants familiar to those of us who have sampled the current generation of consumer products, we can also expect systems that exhibit greater autonomy, improved communication skills and specialized expertise on a par with or exceeding that of humans lacking augmentation. We can also expect technology that will make it possible for us to seamlessly integrate advanced capabilities with our innate human cognitive apparatus utilizing increasingly powerful and invasive brain computer interfaces. It is inevitable that consumers will crave and engineers will invent technologies that provide an edge — an edge that will quickly become the new norm.
This will be just the beginning of how intelligent machines become more deeply integrated into human society, both as cognitive enhancements and as autonomous agents that will no doubt become increasingly demanding of rights on a par with those accorded humans. In the near term we have an opportunity to solve a wide range of human problems even as we come to grips with the possibility of AI systems that deserve to be treated with the same respect we currently reserve for one another. The goal here is not to anticipate cross-species conflict or suggest how we might resolve such conflicts. The goal is to explore the options for our own evolution even as we invent the possibilities for own creations to evolve.
Making predictions even a few years out is difficult. Making predictions a few decades out is best left to science fiction writers. Accurate prediction is made much harder as a consequence of technologies accelerating the pace of change to such an extent it is almost impossible for us to really comprehend. In any case, long-term prediction is a fools errand and we are generally better off thinking about how to apply ourselves to solving today's problems given that they aren't likely to disappear without our intervention. In this and subsequent chapters, we focus on how to make the best of what is likely to transpire technologically in the ten years or so.
2.2 Thinking About Thinking
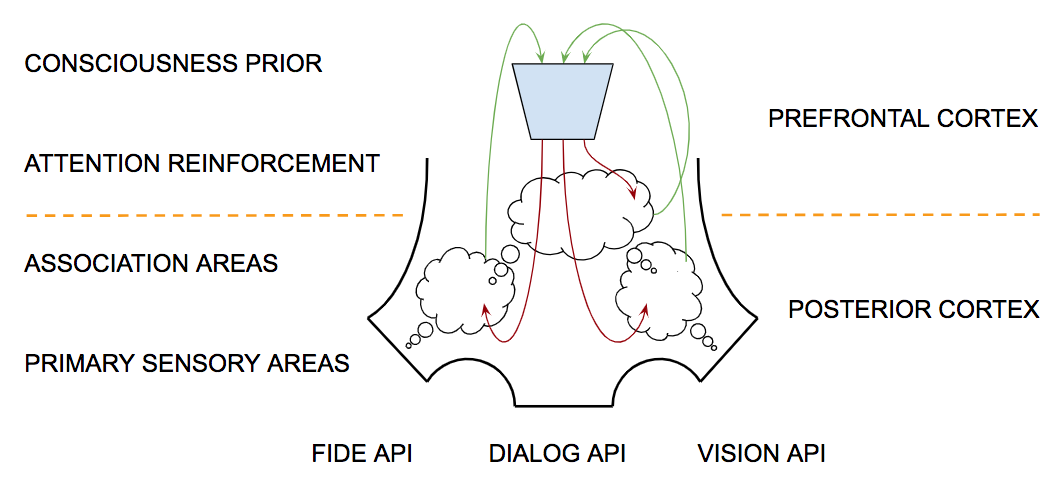
This chapter provides the technical basis for making reasonable predictions about the development of AI technology over the next decade. I think it's important the reader understand the technology well enough to form their own opinion about how this technology might make a difference within our lifetimes. The story is complex in large part because it involves a merging of human and machine intelligence. The focus in this chapter is on how our understanding of one informs the design of the other.
But there is another advantage of the way this chapter and the book as a whole are organized. Artificial neural networks are simpler than biological neural networks. They were developed to understand biological networks as computing machines. In much the same way as the digital abstraction makes it possible to design digital computers with analog components, the artificial neural network abstraction (ANNA) allows us to ignore the details of how neurons function while retaining a level of description that provides insight into how human think.
Cognitive neuroscientists routinely employ concepts from artificial intelligence in order to explain complex phenomena that would be difficult to explain in terms of genes, molecules and basic chemistry. ANNA serves to bridge the conceptual gap between neurons and behavior. The goal is to use ANNA to explain how human brains accomplish basic cognitive skills, to demonstrate how machines can emulate such skills, and to describe how we can engineer autonomous systems and powerful cognitive prostheses that enhance our innate cognitive abilities.
The reader is led to imagine a recurring cycle of activity that begins at the periphery of our bodies as we gather information through our senses and engage with the world through our limbs. Information from multiple sensory modalities is combined to create abstract representations that we consciously choose to attend to and by doing so conjure up memories of related experience that we then apply to engaging both the complex physical world that we inhabit and the equally complex intellectual world that defines our social and cultural milieu.
This cycle is explored further by considering how we can take what we have learned about human cognition to build artificial systems of the sort alluded to above. In this case, we consider the design of a highly capable digital apprentice that would work with and learn from a human software engineer in writing computer programs as an initial step in bootstrapping the next generation of autonomous agents and ultimately creating a world in which intelligent machines and augmented and baseline humans live and work together toward shared goals.
2.3 Programmer's Apprentice
The original programmer's apprentice was the name of project initiated at MIT by Chuck Rich and Dick Waters and Howie Shrobe to build an intelligent assistant that would help a programmer to write, debug and evolve software. Our version of the programmer's apprentice is implemented as an instance of an hierarchical neural network architecture. It has a variety of conventional inputs that include speech and vision, as well as output modalities including speech and text. In these respects, it operates like most existing commercial personal assistants.
It differs substantially, however, in terms of the way in which the apprentice interacts with the programmer. It is useful to think of the programmer and apprentice as pair programming, with the caveat that the programmer is in charge, knows more than the apprentice does — at least initially, and is invested in training the apprentice to become a competent software engineer. One aspect of their joint attention is manifest in the fact that they share a browser window. The programmer interacts with the browser in a conventional manner while the apprentice interacts with it as though it is part of its body directly reading and manipulating the HTML using the browser API. The browser serves both programmer and apprentice as and encyclopedic source of useful knowledge as well as another mode of interaction and teaching.
Suppose you could merely imagine a computation, and a digital prostheses, an extension of your biological brain, would turn it into code that instantly realizes what you had in mind. Imagine looking at an image, dataset or set of equations and wanting to analyze and explore its meaning as an artistic whim or part of a scientific investigation. I don't mean you would use an existing software suite to produce a standard visualization, but rather you would make use of an extensive repository of existing code to assemble a new program analogous to how a composer draws upon a repertoire of musical motifs, themes and styles to construct new works, and tantamount to having a talented musical amanuensis who, in addition to copying your scores, takes liberties with your prior work, making small alterations here and there and occasionally adding new works of its own invention, novel but consistent with your taste and sensibilities.
Perhaps the interaction would be wordless and you would express your objective by simply focusing your attention and guiding your imagination, the prostheses operating directly on patterns of activation arising in your primary sensory, proprioceptive and associative cortex that have become part of an extensive vocabulary that you now share with your personal digital amanuensis. Or perhaps it would involve a conversation conducted in subvocal, unarticulated speech in which you specify what it is you want to compute and your assistant asks questions to clarify your intention and the two of you share examples of input and output to ground your internal conversation in concrete terms.
More than thirty years ago, Charles Rich and Richard Waters published an MIT AI Lab technical report [102] entitled The Programmer's Apprentice: A Research Overview. Whether they intended it or not, it would have been easy in those days for someone to misremember the title and inadvertently refer to it as "The Sorcerer's Apprentice" since computer programmers at the time were often characterized as wizards and most children were familiar with the Walt Disney movie Fantasia, featuring music written by Paul Dukas inspired by Goethe's poem of the same name73. The Rich and Waters conception of an apprentice was certainly more prosaic than the idea described above74, but they might have had trouble imagining the amount of code available in open-source repositories and the considerable computational power we carry about on our persons or can access through the cloud.
In any case, you might find it easier to imagine describing programs in natural language and supplementing your descriptions with input-output pairs. The programs could be as simple as short shell scripts used to extract text fragments from large numbers of files or as complicated as powerful simulators and optimization algorithms. The point is that there is a set of use cases that are within our reach now and that set will grow as we improve our natural language understanding and machine learning tools. The scope of applications within reach today is probably larger than you think and our growing understanding of human cognition is helping to substantially broaden that scope and significantly improve the means by which we interact with computers in general and a new generation of digital prostheses in particular. Here are just a few of the implications that might follow from pursuing a very practical and actionable modern version of The Programmer's Apprentice:
Develop systems that enable human-machine collaboration on challenging design problems including software engineering:
The objective of this effort is to develop digital assistants that learn from continuous dialog with an expert software engineer while providing initial value as powerful analytical, computational and mathematical savants. Over time these savants learn cognitive strategies (domain-relevant problem solving skills) and develop intuitions (heuristics and the experience necessary for applying them) by learning from their expert associates. By doing so these savants elevate their innate analytical skills allowing them to partner on an equal footing as versatile collaborators — effectively serving as cognitive extensions and digital prostheses, thereby amplifying and emulating their human partner's conceptually-flexible thinking patterns and enabling improved access to and control over powerful computing resources.
Leverage and extend the current state of the art in machine learning by integrating human and machine intelligence:
Current methods for training neural networks typically require substantial amounts of carefully labeled and curated data. Moreover the environments in which many learning systems are expected to perform are partially observable and non-stationary. The distributions that govern the presentation of examples change over time requiring constant effort to collect new data and retrain. The ability to solicit and incorporate knowledge gleaned from new experience to modify subsequent expectations and adapt behavior is particularly important for systems such as digital assistants with whom we interact and routinely share experience. Effective planning and decision making rely on counterfactual reasoning in which we imagine future states in which propositions not currently true are accommodated or steps taken to make them true [53]. The ability for digital assistants to construct predictive models of other agents — so-called theory-of-mind modeling — is critically important for collaboration [101].
Draw insight from cognitive and systems neuroscience to implement hybrid connectionist and symbolic reasoning systems:
Many state-of-the-art machine learning systems now combine differentiable and non-differentiable computational models. The former consist of fully-differentiable connectionist artificial neural networks. They achieve their competence by leveraging a combination of distributed representations facilitating context-sensitive, noise-tolerant pattern-recognition and end-to-end training via backpropagation. The latter, non-differentiable models, excel at manipulating representations that exhibit combinatorial syntax and semantics, are said to be full systematic and compositional, and can directly and efficiently exploit the advantages of traditional von Neumann computing architectures. The differences between the two models are at the heart of the connectionist versus symbolic systems debate that dominated cognitive science in 80's and continues to this day [93, 40]. Rather than simulate symbolic reasoning within connectionist models or vice a versa, we simply acknowledge their strengths and build systems that enable efficient integration of both types of reasoning.
Take advantage of advances in natural language processing to implement systems capable of continuous focused dialog:
Language is arguably the most important technical innovation in the history of humanity. Not only does it make possible our advanced social skills, but it allows us to pass knowledge from one generation to the next and provides the foundation for mathematical and logical reasoning. Natural language is our native programming language. It is the way we communicate plans and coordinate their execution. In terms of expressiveness, it surpasses modern computer programming languages, but its capability for communicating imprecisely and even incoherently, and our tendency for utilizing that capability makes it a poor tool for programming conventional computers. That said it serves us well in training scientists and engineers to develop and apply more precise languages, and its expressiveness along with our facility using it make it an ideal means for humans and AI systems to collaborate. The consolidation and subsequent recall and management of episodic memory is a key part of what makes us human and enables our diverse social behaviors. Episodic memory makes it possible to create and maintain long-term relationships and collaborations [100, 83, 92].
Think seriously about how such technology might ultimately be employed to build brain-computer-interfaced prostheses:
This exercise primarily relies on the use of natural language to facilitate communication between the expert programmer and apprentice AI system. The AI system learns to use natural language in much the same way as a human apprentice would — as a flexible and expressive tool to capture and convey understanding and recognize and resolve misunderstanding and ambiguity. The AI system interacts with computing hardware through a highly instrumented integrated development environment. Essentially, the AI system can read, write, execute and debug code by simply thinking — reading and writing to a differentiable neural computing interface [48]. It can also directly sense code running by reading messages generated by the code, parsing output from the debugger and collecting and analyzing program traces. The same principles could be applied to develop digital prostheses employed for a wide range of intelligence-enhancing human-computer interfaces.
2.4 Memory and Computation
The fields of cognitive and systems neuroscience75 are playing an important role in directing and accelerating research on artificial neural network systems. Much of this work predates and helped give rise to the especially exciting work on connectionist models in the 1980s. However, in the nearly 40 intervening years, a great deal of progress has been made, much of it due to improved methods for studying the behavior of awake behaving animal subjects and human beings in particular. Indeed, this work is undergoing a renaissance fueled by even more powerful methods for observing brain activity in human beings in the midst of solving complex cognitive tasks.
The field of automated programming, after decades of steady, often quite practical research on using symbolic methods — much of it originating in labs outside the United States, is seeing a renewed interest in artificial neural networks. It remains to be seen whether artificial neural networks will have a significant impact on code synthesis, however there appear to be opportunities to leverage what we know about both natural and artificial neural networks to make progress, and hybrid systems that combine both connectionist and traditional symbolic methods may have the best chance of pushing the state-of-the-art significantly beyond its present level.
Understanding human intelligence, advancing artificial intelligence and automating the field software engineering so as to accelerate progress on the first two! Critics can't complain we haven't set ourselves lofty goals. They may however argue that we have stretched ourselves too thin. I maintain that these three areas of science and engineering offer a confluence of ideas that are leading to new solutions and in the process fueling their own advancement. Already artificial intelligence is being used to construct models from brain data and automated programming is being used to learn new artificial neural network architectures. In the following, we apply lessons from neuroscience to the design of digital assistants.
Memory and computation in biological neural networks are collocated in the sense that neurons store information (data) and perform computations (calculations) involving that information. There is no direct analog of a computer program since the calculations are determined by the current internal state of the neuron and the information provided by its neighbors. This is in contrast with conventional computing on machines based on the von Neumann architecture in which memory and computation are kept separate. To perform computations, instructions and data stored in random access memory (RAM) are copied into special registers in the arithmetic and logic unit (ALU) where instructions are carried out on data using ALU hardware and the results copied back into RAM. In von Neumann machines, programs are also stored in RAM as sequences of instructions. The operations performed by the ALU are general in that any program written can be reduced to ALU operations.
In the case of the programmer's apprentice, much of the relevant information is about computing and software and includes the type of items that software engineers routinely think about in plying their trade such as algorithms, data structures, interfaces, programs, subroutines and tools such as assemblers, compilers, debuggers, interpreters, parsers and syntax checkers. Then there are the things that programmers generally do not think about explicitly but that concern how they solve problems and organize their thoughts, including, for example, the design strategies we learn in computer science courses such as divide-and-conquer, dynamic-programming and recursion. Finally, there is strategic organizational information of a sort that plays a role in any complex individual or collaborative effort including plans, tasks, subtasks, specifications and requirements.
All of this information has to be encoded in memory and made accessible when required to perform cognitive tasks. Information, whether in a computer or a brain, tends to move around depending on what is to be done with it, and, at least in biological brains, it is constantly changing. In our biological brains, it is difficult if not impossible to think about something without changing it. In building systems inspired by biological brains we have somewhat more control over such changes, but control comes at a cost. We make no distinction between concrete and abstract thoughts — all thoughts are abstract whether they represent atoms or bits. We will on occasion refer to memories as being short- or long-term but the distinction doesn't begin to address real issues. When we talk about episodic memory, it may seem that we are referring to some sort of permanent or archival memory, but that's not the case in biological systems for reasons that make sense from an evolutionary standpoint and we may decide to follow suit in building artificial systems.
2.5 Cognitive Neuroscience
The study of human cognitive function at the systems level primarily consists of human subjects performing cognitive tasks in a functional Magnetic Resonance Imaging (fMRI) scanner that measures brain activity as reflected in changes in local blood oxygen levels associated neural activity. These studies localize functional activity in space and time to construct cognitive models by measuring the correlation between regions of observed brain activity and the steps carried out by subjects in solving problems. While these studies have played an important role in our understanding of human cognition, they are limited by their relatively poor spatial (several millimeters) and temporal (hundreds of milliseconds) resolution when compared with more invasive methods. That said, fMRI is currently the best method for whole brain imaging of awake, behaving human subjects. This may change with recent improvements to magnetoencephalography (MET) technology which as better comparable spatial and substantially better temporal (milliseconds).
In addition to localizing brain activity correlated with cognitive functions, Diffusion Tensor Imaging (DTI) can be used for tractographic reconstructions to infer white-matter connections between putative functional regions. White matter corresponds to myelinated axons and serves to connect neurons that are relatively far apart — myelin increases the velocity at which electrical impulses propagate along myelinated fibers in both the central and peripheral nervous system and is especially important in large brains where faster signal conduction speeds neural processing. By using anatomical landmarks to localize functional regions and tractography to trace the white-matter connections between functional regions, researchers can analyze time-series consisting of the activity patterns recorded at fixed intervals while subjects perform standardized cognitive tests, for the same subject on multiple trials, between subjects or averaged over multiple trials.
For example, in one study, economists investigate how neural activity patterns vary as subjects decide how to bet in two different scenarios. In first scenario, subjects select from a deck of 20 cards composed of 10 red and 10 blue cards — this is referred to as the risky bet, and, in the second scenario, the deck has 20 red or blue cards, but the composition of the red and blue cards is completely unknown — referred to as the ambiguous bet. A successful bet on a color wins a certain amount of money if a card with the chosen color is drawn. Otherwise the participant loses a certain amount of money.
The details aren't particularly relevant to our discussion; however, when asked to choose between a risky bet and an ambiguous bet, subjects prefer the risky option. What is relevant in terms our understanding the parts of the brain figure most prominently in this choice, is that Xu et al [140] found that two adjacent brain regions in the medial prefrontal cortex (MPFC) conveyed distinct decision signals, specifically, the dorsal MPFC was more activated when individuals experienced higher level of risk. In contrast with this finding, the ventral MPFC was parametrically modulated by the received gain or loss. This sort of study contributes to our understanding of how functional regions play a role in decision making under uncertainty.
If you are interested in how humans make decisions, fMRI studies can provide insight into the role that different brain regions play at different stages in the decision-making process, but it is much harder to drill down to the cellular or molecular level in order to understand what's going on in circuits comprised of individual neurons or in more diffuse signaling pathways such as the neurotransmitter systems originating in the brain stem that control the release of dopamine, seratonin and acetylcholine76. Studies that involve mice on the other hand allow much more freedom in studying behavior in general and decision making in particular. Researchers can use optogenetic probes to systematically dissect the neural circuits. For example, there are genetically-engineered — or transgenic — mice that allow photostimulation or photoinhibition of genetically defined populations of neurons, e.g., specific cell types, with high temporal and spatial resolution [2]. As an example of the power of these tools, researchers have discovered a mode of inhibitory control in which inhibitory neurons specifically suppress the firing of other inhibitory neurons thereby inhibiting inhibition and by so doing effectively facilitating exitation [97].
More relevant to our interest in the logical and mathematical thinking that goes into programming, researchers have made progress uncovering the neural basis of numerical cognition. Evidence from human neuroimaging, primate neurophysiology and developmental neuropsychology reveal that humans and animals share a system of approximate numerical processing [30]. Stanislas Dehaene, first author on the cited paper, has written extensively on what he refers to as the number sense [31] and we look at his model of consciousness later in this chapter [32]. Krueger et al [69] builds on the work of Dehaene and his colleagues to provide evidence that a network of regions in the prefrontal cortex and adjacent sulci are implicated in solving abstract mathematical problems exhibits similar patterns of activity. At this point, I think it will help if we take a closer look at the anatomy (structure) and physiology (function) of the human brain and, in particular, the functional regions and how these regions communicate with one another. It's a useful orientation exercise for all of us and in particular for those of us who benefit from visual aids in understanding complicated processes that are physically realized in structural configurations that reveal aspects of their collective function.
2.6 Anatomy and Physiology
The human brain is a highly evolved survival machine. Its purpose is to enable us to survive long enough to reproduce and pass on our genes. Given that it is a product of natural selection forced to rely on its existing design in order to live long enough to improve upon that design under selective pressure, it's not surprising that it is quite unlike the engineered products that humans manufacture. It's also not surprising that human beings have been curious about the brain for as long as we knew we had one and that the language we use to describe the structure and function of the brain reflects the long history of its study. Even the very basic anatomy of the brain is still described using a vocabulary that goes back centuries.
On the one hand, anterior, posterior, superior and inferior are used to identify the front, back, top and bottom of the brain for some purposes. Whereas rostral, caudal, dorsal and ventral are employed to specify the same coordinates for other purposes. Medial can be used to refine location within the brain as a whole or within a specified subcomponent. Terms like telencephalon, diencephalon, etc. describe subdivisions of the embryonic vertebrate brain and can be used to refer collectively to the adult regions they mature into, e.g., the telencephalon develops into the two cerebral hemispheres, including the cerebral cortex and a number of smaller subcortical structures.
In our discussions, we'll largely ignore the fact that the much of the brain and the cortex in particular is divided into two hemispheres with similar structure though somewhat different function. In talking about the cortex, we will often refer to the lobes that comprise each hemisphere, including the occipital lobe near the back of the brain encompassing the early visual system, the temporal lobe near the temple that is responsible for hearing and implicated in language, the parietal lobe including the somatosensory cortex, and the frontal lobe including the primary motor and premotor cortex as well as circuits involved in executive control, problem solving and consciousness.
Of course, the brain is two-dimensional and highly structured. The cortex can be thought of as a sheet of neural tissue consisting of several layers such that each layer plays a different role and often involves different types of neurons in different patterns of connectivity. If you stretched it out flat on a table, the cortex would be about the size of a large dinner napkin, but when folded up to fit within the human cranium it is divided into ridges referred to as gyri — singular gyrus — separated by fissures called sulci — singular sulcus — so that areas that appear near to one another on the surface may be at some distance from one another.
All of this can be enormously confusing to the uninitiated. Fortunately, we won't spend a lot of time talking about anatomical details. Our objective is to design artificial neural network architectures that emulate parts of the brain that humans employ in solving practical problems, and combine these component architectures to design end-to-end systems to assist human engineers and scientists in their research. We aren't interested in slavishly simulating human behavior with all its idiosyncrasies, but rather exploit what we know about the brain in designing these assistants and re-engineer human capabilities when reasonable to do so.
We'll spend a good deal of our time talking about structures in the cerebral cortex including the so-called neocortex in the mammalian brain which is regarded as the most recently evolved part of the cortex. We'll also spend some time talking about the cerebellar cortex generally referred to as the cerebellum, especially with respect to its recently-evolved circuitry complementing that found in the neocortex.
The primate cortex appears to be tiled with columnar structures referred to as cortical columns. Some neuroscientists believe that all of these columns compute the same basic function. However, there is considerable variation in cell type, thickness of the cortical layers, and the size of the dendritic arbors to question this hypothesis. The prefrontal cortex is populated with a type of neuron, called a spindle neuron, similar in some respects to the pyramidal cells found throughout the cortex, that allow rapid communication across the large brains of great apes, elephants, and cetaceans. Spindle neurons are abundant in humans and play an important role in consciousness and attentional networks.
Figure 6 presents a stylized drawing of a human brain shown from the side so that only one hemisphere is visible. The drawing shows the major functional areas of the human cortex. In the following we provide a rough characterization of their function and how they contribute to the realization of human cognition in general and the programmer's apprentice in particular. When necessary, we introduce relevant subcortical circuits such as the basal ganglia and hippocampal nuclei and provide additional anatomical detail as required to explain their function.
| |
| Figure 6: A highly stylized rendering of the major functional areas of the human cortex. Highlighted regions include the occipital lobe shown in shades of green including the primary visual cortex; the parietal lobe shown in shades of blue including the primary somatosensory cortex; the temporal lobe shown in shades of yellow including the primary auditory cortex; and the frontal lobe shown is shades of pink including the primary motor and prefrontal cortex. The region outlined by a dashed line on the right is Broca’s area and it is historically associated with the production of speech and hence its position relative to the motor cortex. The region outlined by a dashed line on the left is Wernicke’s area and it is historically associated with the understanding of speech and hence its position relative to the sensory cortex. | |
|
|
Figure 6 shows the four lobes of the primate brain plus several functional areas that will figure prominently in this chapter. Here are several additional terms that appear frequently enough that it makes sense to give each one a short description and convenient abbreviation:
prefrontal cortex (PFC) including attention, conscious access, reward-based-learning and executive control [134, 68];
entorhinal-hippocampal complex (EHC) in its role as primary interface between the hippocampus and neocortex [92, 89];
global workspace (GW) broadly distributed cortical circuits connected through long-range excitatory axons77 [33, 4];
basal ganglia (BG) for its role in action selection and dynamic gating to direct input to the prefrontal cortex[91, 68];
semantic memory system (SMS) including areas of the brain responsible for mathematical and abstract thought [126, 9];
Your primary peripheral sensory systems, e.g., auditory, visual, touch, etc, tend to produce representations that are similar from one individual to another. The brains of most animals are genetically predisposed to organize themselves using an incredible array of chemotactic and cellular-scaffolding techniques that materials scientists would love to have for building self-assembling nanoscale machines. From a very early stage in fetal development the structures are in place to ensure that the primary auditory and visual areas of the cortex will end up in their respective locations in the temporal and occipital lobes and connect to their respective sensory apparatus.
It makes sense that our genes are programmed to enforce this regularity but it only goes so deep, in part because there's not enough information in our genome to precisely determine every neuron and every synapse in the adult brain, but more so because the body needs some flexibility to deal with unforeseen consequences. For example, there is some evidence to suggest that, if one were to have a mutation resulting in the auditory and visual nerve fibers being reversed, the brain would utilize its plasticity to accommodate and see with neural circuits that were designed to hear and hear with those designed to see [63, 118].
If such a reversal were to happen, the result is certainly not likely to be optimal, but it could mean the difference between living long enough to procreate and dying without passing on your genes. The main point here is that we seem to have enough flexibility in how and what we can represent in our brains to deal with the fact that natural selection hasn't had enough time to redesign our brains so that we can manage to learn how to perform mathematics in our heads and understand quantum electrodynamics well enough to design the next generation of semiconductors. In particular, the further we stray from the periphery, the more distinctive / idiosyncratic our encoding of personal events and multi-modal sensor experiences.
Generally when we use the term "cortex", we mean the cerebral cortex. The control system involving the cerebellar cortex or cerebellum, the cerebral cortex and number of subcortical areas including the basal ganglia is one of the most interesting and neglected systems in the mammalian brain and primates in particular. It is often described in terms of a control theoretic block diagram consisting of separate transfer functions as shown here. Contrary to our original understanding of the cerebellum as primarily involved in orchestrating the motor activity controlling fine movement, we now know that the primate neocortex in concert with recently-evolved augmentation of the cerebellum enable human beings to transfer abstract thinking such as that involved in solving algebraic equations from the cerebral to the cerebellar cortex allowing us to carry out such calculations with significantly greater speed and accuracy. Imagine how an experienced software engineer might take advantage of this capability to facilitate thinking about programs, and then think about how we might develop an architecture for the programmer's apprentice that employs a similar strategy.
2.7 Models of Human Memory
There are two major memory systems in the human brain. One is called explicit, or declarative, memory, and it enables us to remember the people, places, objects and events in our lives. In keeping with its name, we are generally conscious when accessing declarative memory and so can report on what we remember. We distinguish between two types of declarative memory, episodic and semantic, in discussing how different types of memory support cognitive functions78.
The second type of memory is implicit, or non-declarative, memory, and serves to encode motor and perceptual skills that we perform automatically. We access non-declarative memory when we perform such skills or practice them to improve our performance. We generally are not conscious of what we are doing when performing these skills. Indeed, attempting to think about what we are doing often impairs performance.
Explicit memories are encoded by the hippocampus, entorhinal cortex and perirhinal cortex, but are consolidated and stored in the temporal cortex and elsewhere. In the case of implicit memory, the prefrontal cortex, parietal cortex, and cerebellum play a role in learning motor skills. The cerebellum is important, as it is required to coordinate sequences of movement required for skilled motion and timing, but also plays a role in cognitive function [13].
We also distinguish between short-term and long-term memory. The former lasts at most a few minutes unless skillfully rehearsed, while the latter can remain available for days, weeks or even years. In the human brain, short-term memory results from strengthening existing connections, while long-term memory results in the growth of new synapses and, in some cases, the birth of new neurons. We discuss several novel ANN memory systems in this chapter.
Human episodic memory is one of the most important elements in determining who we are and how we relate to others. It is critical in reasoning about what's going on in other minds and plays a central role in our social interactions. Not surprisingly episodic memory engages many cortical and sub cortical regions of the primate brain. If one were to pick out a single locus of activity relating to episodic memory it would probably be the entorhinal area corresponding to Brodmann areas 28 and 34 shown here highlighted in yellow. The entorhinal cortex is located in the temporal lobe in close proximity to the hippocampus, but this area is merely the hub of a great deal of activity spread throughout the brain.
The hippocampus is perhaps best known for its role in supporting spatial reasoning. A type of pyramidal neuron called a place cell has been shown to become active when an experimental animal enters an area of a maze that it has visited before. However, the hippocampus plays a much larger role in memory by representing not just the "where" of experience but also the "when". The manner in which we employ short- and long-term memory is very different. We might construct a representation of our current situation in short-term memory, drawing upon our long-term memory to provide detail.
The two memory systems are said to be complementary in that they serve different purposes, one provides a record of the past while the other serves as a scratchpad for planning purposes. In retrieving a memory it is possible that we "corrupt" the long-term memory in the process of subsequent planning. This isn't simply an academic question, it is at the heart of how we learn from experience and employ what we've learned to think about the future. Our memory systems enable us to imagine solutions to problems we have never before encountered, and they account for a good deal of our incredible adaptivity.
2.8 Neural Net Terminology
This chapter is intended to be self contained. For those of you who skipped over the previous chapter, we begin by reviewing the terminology for talking about neural networks, starting with basic units that can be assigned numerical values and are organized in stacks of layers, along with connections between units in adjacent layers that are weighted and stored in tables that represent the strength of the connections.
Connections are said to be directed originating from a unit in one layer and terminating at a unit in another. Units can have more than one outgoing connection as well as multiple incoming connections and generally units in a given layer don't connect to units in the same layer except in the case of recurrent connections where information stored in a unit at time \({t}\) is said to feed back to units at time \({t+1}\).
A neural network model consists of multiple layers arranged in an architecture. Mathematically, the units correspond to scalar variables, the layers to vectors, the tables of connection weights to matrices and the neural network model to a function from inputs — the units in one or more layers that have no incoming connections — to outputs — the units in layers with no outgoing connections.
Though generally discouraged, since the analogy doesn't begin to do justice to the complexity of biological neural networks, practitioners sometimes refer to the units as neurons and the connections as synapses. The connection weights are determined by training a model with data that consists of pairs of input and output assignments, and exploiting the fact that the network functions are differentiable and hence amenable to standard optimization techniques.
The property of being differentiable allows us to adjust all of the weights in a model at once using an objective function that defines what it means to have a good model. We can evaluate how each of the weights in a model contributes to the changes in the objective function when evaluated with respect to one pair of input and output assignments or a batch of such pairs, and then adjust the weights so as to improve the model performance as measured by the objective function.
Training a model involves by randomly selecting individual pairs or batches until we can no longer improve performance. Supervised learning requires labeled data that is often hard to come by. Unsupervised learning doesn't need labels but requires a method of evaluating performance without explicitly being given the correct answer. Later in this chapter, we also explore reinforcement learning in which the model receives intermittent rewards for making progress toward a goal, e.g., winning at chess, and has to figure which of its earlier actions actually contributed to the win, e.g., taking the Queen's knight early in the game.
The basic artificial neural network architecture consists of a hierarchy of specialized networks with a relatively dense collection of feedforward and feedback connections that enable recurrent state, attentional focus and the management of specialized memory systems that persists across different temporal scales. Individual networks are specialized to serve different types of representation, employing convolutional networks, gated-feedback recurrent networks and other network architectures introduced in the previous chapter as components for constructing more complicated architectures.
All of these networks are distributed representations of one sort or another, many of which were developed by the early pioneers in the nascent field of connectionism and featured in the PDP — Parallel Distributed Processing — books that we discussed in the previous class. Typically, they encode information in high-dimensional vector spaces such that different dimensions can be trained to represent different features allowing attentional mechanisms to emphasize or modify encodings so as to alter their meaning in a manner analogous to variable substitution in traditional symbolic systems.
There are a lot of details that engineers have to think about in designing neural network architectures training a model with billions of weights, but this summary account should suffice for understanding the concepts explored in this chapter and you can always return to the previous chapter if you want to dig a little deeper. Part of our goal in developing artificial neural networks is to gain insight into how biological networks — and our brains in particular — actually function.
Semantic Memory
Our objective in developing systems that incorporate characteristics of human intelligence is three fold: First, humans provide a compelling solution to the problem of building intelligent systems that we can use as a basic blueprint and then improve upon. Second, the resulting AI systems are likely to be well suited to developing assistants that complement and extend human intelligence while operating in a manner comprehensible to human understanding. Finally, cognitive and systems neuroscience provide clues to engineers interested in exploiting what we know concerning how humans think about and solve problems. In this appendix, we demonstrate one attempt to concretely realize what we've learned from these disciplines in an architecture constructed from off-the-shelf neural networks.
The programmer's apprentice relies on multiple sources of input, including dialogue in the form of text utterances, visual information from an editor buffer shared by the programmer and apprentice and information from a specially instrumented integrated development environment designed for analyzing, writing and debugging code adapted to interface seamlessly with the apprentice. This input is processed by a collection of neural networks modeled after the primary sensory areas in the primate brain. The outputs of these networks feed into a hierarchy of additional networks corresponding to uni-modal secondary and multi-modal association areas that produce increasingly abstract representations as one ascends the hierarchy — see Figure 7.
| |
| Figure 7: The architecture of the apprentice sensory cortex including the layers corresponding to abstract, multi-modal representations handled by the association areas can be realized as a multi-layer hierarchical neural network model consisting of standard neural network components. This graphic depicts these components as encapsulated in thought bubbles of the sort often employed in cartoons to indicate what some cartoon character is thinking. Analogously, the technical term "thought vector" is used to refer to the activation state of the output layer of such a component. All of the bubbles appear to contain networks with exactly the same architecture, where one might expect sensory modality to dictate local architecture. The hierarchical architecture depicted here is modeled after the mammalian neocortex that appears to be tiled with columnar component networks called cortical columns that self-assemble into larger networks and adapt locally to accommodate their input. In practice, it may be necessary to engineer modality-specific networks for the lowest levels of the hierarchy — analogous to the primary sensory and motor areas of the neocortex, but more general-purpose networks for the higher levels in the hierarchy — analogous to the sensory and motor association areas. | |
|
|
2.9 Reinforcement Learning
In the previous chapter we focused on supervised learning depending on labeled data consisting of input-output samples where the objective function is a measure of how well the system can predict the output given the input, or unsupervised learning depending on unlabeled consisting of input-only samples where the objective function is a measure of fitness for a given purpose that applies to any input sample, e.g., the size of the output in bits for the purpose of compressing image data.
In most current applications, all of the learning occurs prior to the use of the fully trained model in a production setting, but this approach is changing as we tackle more complicated problems in dynamic environments that require altering what we learned in light of new information — with or without supervision — and learning entirely new skills and knowledge, possibly with the benefit of intermittent feedback, as we take on new challenges "learning on the job" as it were.
Reinforcement learning is a method of learning that lends itself well to continued learning on the job during which the learning system often only receives feedback upon completing a particular task or achieving a goal and then generally without any detail concerning what exactly the system did to deserve that feedback, as in the case where, having played an entire game of chess, the novice receives little more than is obvious from looking at the game board, i.e., a win, loss or draw.
There are several sources of uncertainty in reinforcement learning that make learning hard. Feedback could be provided precisely when the agent performs a specific action that warrants some approbation, but that is rare. Feedback is sometimes ambiguous or graded using an obscure metric. Understanding feedback — its valence — positive or negative — and weight — just how seriously should one interpret it — requiring a form of sentiment analysis not unlike what is required for ranking movies by reading reviews and comments on web pages. Learning to understand feedback provided in natural language would probably qualify for passing the Turing test.
Another source of uncertainty arises due to the timing of feedback. If the only feedback you get for, say, winning at chess, is at the end of the match when the winner is announced, then it's difficult to understand what you did that warranted praise, sympathy or derision. A reinforcement learning system needs some form of intermediate rewards in order to become a chess champion or talented software engineer. Judging progress in solving complex problems is itself a difficult learning problem and can be characterized as a prediction problem. It's probably instinctual but requires practice and coaching to become good at it.
The objective of reinforcement learning (RL) is to learn a policy that maps from an agent's representation of the current situation or state to the best action to take in that situation. In service to that goal, the agent learns a value function that given a state \({s}\) and action \({\alpha}\) returns a number that represents the expected value (reward) of performing the action in that state. In chess, a state corresponds to an arrangement of pieces on the board and an action to a legal move.
A little more precisely, the neural network for an RL system defines a value function \({\varphi}\) that maps each state-action pair \({(s, \alpha)}\) to a real number \({v}\) where \({s \in{} S}\), \({\alpha\in{} A}\) and \({v \in{} \mathbf{R}}\) and implements a policy \({\pi: S \mapsto{} A}\) such that \({\pi(s) = \alpha}\) for \({\alpha}\) maximizing \({\varphi(\alpha, s)}\).
Realistically, the state of an RL-based chess playing system is likely to be much more than just an arrangement of pieces on chess board. In practice, the state also includes a representation of the moves made in the current game, possibly information relating to the current opponent and likely information relating to previous games and to the systems current stragegy and assessment of strengths and weaknesses. Indeed, the context for any action will include a good deal of information gathered together from multiple memory systems.
This book emphasizes how our understanding of the human brain has informed our efforts to build artificial brains and so, in the following section and later in Section IGNORE, we introduce two examples illustrating how our study of biological neural networks has guided us in designing artificial neural networks.
The example biological networks support capabilities associated with human cognition that are uniquely human, at least in the degree to which we have these capabilities when compared with other animals and the extent to which we have applied them in service to the advancement of human welfare, culture and the pursuit of knowledge.
Action Selection
In this section, we consider the biological basis for action selection and higher order executive control in human beings. In particular we looks at the neural circuits generally considered to be our best guess about how reinforcement learning in implemented in the brain. These circuits assist in formulating and carrying out plans to achieve our goals and solving complex problems that require a high degree of attention, the capacity to hold several concepts in mind at a time and the ability to think about how these concepts relate to one another so as to draw new conclusions.
In each case, we start with a simplified introduction to the relevant anatomy, followed by an explanation of how the biological networks support the target capability. Later, we provide an example artificial neural network that supports a related, if not precisely equivalent capability. The two capabilities that we consider are also noteworthy for the fact that each relies upon subcortical regions that every mammal comes equipped with. However, these functional areas have evolved considerably in humans over the last few million years as they have adapted to take advantage of and support the extended capabilities of the mammalian human neocortex.
In contrast with relative simplicity of the neocortical architecture, the basal ganglia consist of several subcortical nuclei that are related by their evolved function, but not so neatly organized structurally, or at least not to the untrained eye used to human engineered artifacts. In the following, we emphasize and simplify some of those nuclei and ignore others to focus the discussion and simplify the biology. The basal ganglia provide the basis for motor activity controlled by circuits in the brainstem and conserved throughout vertebrate evolution for nearly half a billion years. The cerebral cortex has been around in the form of a six-layer sheet tiled with a repeating columnar structure since the early mammals came on the scene in the Jurassic period about 200 million years ago. Our lineage separated from mice around 100 million and from macaques and other old world monkeys around 25 million years ago. The modern human neocortex owes much to these earlier evolutionary innovations but is different in ways that make possible our facility with language, complex social organization and sophisticated abstract thinking. Compared with the basal ganglia, the neocortex is structurally elegant and functionally general.
The basal ganglia have evolved along with our neocortex to provide us with a powerful thinking machine, while at the same time leaving us to make do with some less-than-ideal adaptations components. We can simulate a conventional computer in our heads but are limited to fewer than a dozen memory registers. Most of us can't perform long division in our heads even though we might know the algorithm and aided with paper and pencil carry out the necessary computations to produce an answer. We rely on the same basic cognitive machinery we use to list a few names in alphabetical order to perform all sorts of more complicated cognitive tasks. Even simpler, however, is the basic operation of choosing one several actions to perform next. The basal ganglia play a key role in supporting action selection and it is worth looking at in a little more detail in order get a handle on some of the parts of the brain that figure prominently in human cognition. Recall that the cortex is a sheet of neural tissue more or less homogeneous in terms of its local structure quite unlike almost any other part of the brain except for the cerebellar cortex. The cortex sits on top of a structure called the thalamus which among other things serves as a relay in passing information back and forth between the cortex and various subcortical nuclei.
The basal ganglia consist of a bunch of circuits, of varied size, sometimes but not always consisting primarily of one cell type, sometimes but not necessarily compactly clustered together, sporting projections that seem to wander off aimlessly, but more or less located above the brainstem and below the cortex. As a general principle, if a signal sets off along some path exiting from a circuit, then expect some derivative of that signal to appear later reentering the circuit to serve as feedback. Everything about the brain, and your entire body for that matter, has to be carefully regulated to maintain a dynamic state of the equilibrium, and unlike human designs, evolution is generally not able to cleanly separate the parts of the circuit that, say, perform some computation from the parts that deal with respiration, immune response, waste removal, cell repair, death and regeneration, etc.
| |
| Figure 8: The left panel provides a highly stylized anatomical drawing of the basal ganglia. The block diagram shown in right panel depicts the primary components involved in action selection as functional blocks. The blocks shown in blue represent components in the direct path and are described in the text proper. The blocks shown in light green with dashed borders represent additional components that contribute to the indirect path. The indirect path is described here along with more detail concerning the direct path and additional resources that include links to relevant 2018 class lectures and related papers. | |
|
|
The basal ganglia are depicted in Figure 8.A taking some artistic license to keep things simple. The thalamus along with another structure called the striatum provide the interface between the cortex and basal ganglia. The striatum is a combination of a number of smaller nuclei that are anatomically and functionally related; they include the Globus Pallidus (GP), Putamen and Caudate Nucleus and aside from their function as part of the striatum, only the GP will figure prominently in our discussion and only one part of it — referred to as the internal GP and identified with the "i" subscript to distinguish it from the external part with "e" subscript.
The other players include the Substantia Nigra (SN) which is at one end of the striatum nestled close to the amygdala which is part of the limbic system involved with memory, decision-making and modulating emotional responses, and the Subthalamic Nucleus (STN). You can think of the cortex as integrating sensory and motor information and making suggestions for what action to take next and the amygdala as supplying information pertaining to the possible emotional consequences of taking different actions to be used as input to action selection. Figure 8.B reconfigures these component nuclei into a smaller number of functionally motivated blocks that control two pathways — the direct pathway associated primarily with inhibition and consisting of the internal GP and SN and the indirect pathway playing an excitatory role and consisting of the external GP and STN79.
The lines connecting the functional blocks shown in Figure 8.B imply neural connectivity, with arrows indicating the direction of influence and colors indicating the valence of the influence, green for excitatory and red for inhibitory. In the action selection cycle, the cortex forwards activations that you can think of as suggestions for what action to take next. These suggestions are propagated through the striatum and forwarded along the direct pathway where two stages of inhibitory neurons initially suppress all of the suggestions and propagate signals back the cortex to activate inhibitory neurons that suppress activity at the source. As this cycle continues, an additional process takes place in the indirect path — identified with dashed lines — that weighs the advantages and disadvantages of the proposed actions taking in information from throughout the cortex and adjusting the inhibitory bias accordingly.
Eventually, one proposal wins out and all of the others are suppressed allowing a single preferred action to be executed. This cycle of exploring the options for acting and then selecting a single action to execute is constantly repeated during your waking hours. Additional machinery in the thalamus and brain stem regulates whether or not to forward suggestions for acting during sleep when your cortex receives no sensory input and hence any suggestions for acting uninformed by sensory input are ill-advised if not outright dangerous. The above description doesn't begin to convey the complexity of what's going on at the level of individual neurons. Suffice it to say that the usual perfunctory summary consisting of "the winner takes all" doesn't begin to do it justice. The subtleties arise from the way in which the evidence for and against an action proposal is combined, how ties are broken and deciding when enough evaluation is determined sufficient to make a final choice.
2.10 Attentional Networks
While biological and artificial networks can carry out a lot computations in parallel, there are resource limitations and many activities like reading, speaking and controlled movement are typically, if not fundamentally, serial. In the previous chapter, we discussed the concept of attentional networks that learn to identify what part of our recent experience is most important for our current purposes and make that information available to guide subsequent processing.
Attentional networks take as input activation patterns from multiple sources plus additional input summarizing the current context for the task at hand, e.g., coming up with next word or phrase to speak in a conversation. Based on prior training for the task, the network computes a weighted sum of the input activation patterns and combines it with the context summary to produce an enriched context, e.g., incorporating an earlier comment from the same conversation, in which to decide what do do.
The applications we consider in this chapter require a combination of intensive early training followed by a lifetime of learning on the job. The early training can be thought of in terms of naturally paced development stages from prenatal, through early childhood and extending into early adulthood, along with targetted curriculum-based learning in kindergarten through high school combined with extensive extracurricular training in effective communication and social interaction.
These skills require several specialized memory systems and those memory systems rely on specialized mechanisms for focussing attention and learning what to attend to, and so to start and keep our promise to make this chapter self contained, we review the relevant details and elaborate on the discussion of attention in the previous chapter. While any number of weighty tomes have been written on the subject, we emphasize a general mechanism and focus on its simple neural-network realization.
Start with a multilayer network having two or more separate input layers that represent different information sources originating in the sensory cortex or one of several short- or long-term memory systems, along with an input layer that represents the context for the deliberative function this attentional system serves. For example, the context might represent the state of a conversation and the input sources to memories that might enrich the context with a name, clever comment or change of topic.
Train the network to do a good job of improving conversations by simply rewarding the system if the conversation continues in a satisfying manner. Now that last bit about "conversations continuing in a satisfying manner" might seem a bit of a stretch, but I'm assuming that learning how to carry on a conversation doesn't become important until long after you've learned how to read other people well enough to determine whether or not they are pleased with you. Babies are innately able to do this.
And so, while understanding the neural correlates for, say human visual attention, is still an active area of research important in understanding human cognition, software engineers implementing an attentional component of a larger network needn't concern themselves with the details of how attention is handled in humans, and need only to design a network architecture that accommodates the particular set of inputs and outputs required of the application at hand — see Figure 5.
Long Short-Term Memory (LSTM) models were one of the first really practical recurrent neural-network architectures. Now there are quite a few variations including Gated-Feedback Recurrent Networks (GF-RNN) and convolutional neural networks have been shown to work as well as recurrent models for some problems. There have been several important extensions to RNN models that have considerably extended their range. Here we mention three extensions that are applicable to the programmer's apprentice. All three of these extensions exploit attention in some manner, and they can be combined to design even more capable architectures.
The basic Attentional Interface that we've already encountered allows an RNN model to selectively focus on parts of its input. Neural Turing Machine (NTM) — also called Differentiable Neural Computer (DNC) — models employ external dynamic memory that can be read from and written to under attentional control. Finally, Neural Programmer models learn how to write programs as a means of accomplishing a target task. These programs need not be conventional computer programs and learning to program doesn't require examples of correct programs since the objective function depends on the target task and gradient descent does the rest.
Single-modality sensory information feeds into multi-modal association areas to create rich abstract representations. Attentional networks in the prefrontal cortex take as input activations occurring throughout the posterior cortex. These networks are trained by reinforcement learning to identify areas worth attending to and the resulting policy selects areas to attend to and sustain. This attentional process is guided by a prior that prefers low-dimensional thought vectors corresponding to statements about the world that are either true, highly probable or very useful for making decisions. Humans can sustain only a few such activations at a time. The apprentice need not be so constrained.
To understand attentional networks, think about an encoder-decoder network for machine translation. As the encoder digests each word in the sequence of words that constitute the input sentence, it produces a representation — Geoff Hinton refers to these as thought clouds in analogy to the iconic clouds that you see in comic strips — of the sentence fragment or prefix that it has seen so far. Because the sentence is ingested one word at a time — generally proceeding from left to right — the resulting thought cloud will tend to emphasize the meaning of the most recently ingested words in each prefix.
You could encode the entire input sentence and then pass the resulting representation on to the decoder, but earlier words in the sentence will receive less attention that later words. Alternatively, you could introduce a new network layer that takes as input all of the encodings of the sentence prefixes seen so far and trains the new layer — thereby taking advantage of the power of gradient descent — to produce a composite representation that emphasizes those parts of the input that are most relevant in decoding / generating the next word in the output. Check out this tutorial for more detail.
Conscious Memory
Stanislas Dehaene and his colleagues at the Collège de France in Paris developed a computational model of consciousness that provides a practical framework for thinking about consciousness that is sufficiently detailed for much of what an engineer might care about in designing digital assistants [32]. Dehaene’s work extends the Global Workspace Theory of Bernard Baars [4]. Dehaene’s version of the theory combined with Yoshua Bengio’s concept of a consciousness prior and deep reinforcement learning [81, 84] suggest a model for constructing and maintaining the cognitive states that arise and persist during complex problem solving [6].
Global Workspace Theory accounts for both conscious and unconscious thought with the primary distinction for our purpose being that the former has been selected for attention and the latter has not been so selected. Sensory data arrives at the periphery of the organism. The data is initially processed in the primary sensory areas located in posterior cortex, propagates forward and is further processed in increasingly-abstract multi-modal association areas. Even as information flows forward toward the front of the brain, the results of abstract computations performed in the association areas are fed back toward the primary sensory cortex. This basic pattern of activity is common in all mammals.
The human brain has evolved to handle language. In particular, humans have a large frontal cortex that includes machinery responsible for conscious awareness and that depends on an extensive network of specialized neurons called spindle cells that span a large portion of the posterior cortex allowing circuits in the frontal cortex to sense relevant activity throughout this area and then manage this activity by creating and maintaining the persistent state vectors that are necessary when inventing extended narratives or working on complex problems that require juggling many component concepts at once. Figure 10 suggests a neural architecture combining the idea of a global workspace with that of an attentional system for identifying relevant input.
| |
| Figure 10: The basic capabilities required to support conscious awareness can be realized in a relatively simple computational architecture that represents the apprentice’s global workspace and incorporates a model of attention that surveys activity throughout somatosensory and motor cortex, identifies the activity relevant to the current focus of attention and then maintains this state of activity so that it can readily be utilized in problem solving. In the case of the apprentice, new information is ingested into the model at the system interface, including dialog in the form of text, visual information in the form of editor screen images, and a collection of programming-related signals originating from a suite of software development tools. Single-modality sensory information feeds into multi-modal association areas to create rich abstract representations. Attentional networks in the prefrontal cortex take as input activations occurring throughout the posterior cortex. These networks are trained by reinforcement learning to identify areas of activity worth attending to and the learned policy selects a set of these areas to attend to and sustain. This attentional process is guided by a prior that prefers low-dimensional thought vectors corresponding to statements about the world that are either true, highly probable or very useful for making decisions. Humans can sustain only a few such activations at a time. The apprentice need not be so constrained. | |
|
|
In Dehaene's theory, information about the external world enters the cortex through the thalamus and, with input from subcortical structures responsible for arousal and sleep, generates a signal marking the information available for examination. The raw sensory input is propagated to higher-level processing systems eventually reaching the prefrontal cortex where it is evaluated and selectively made available in short-term memory. The computations required for evaluation and selection can be modeled by attentional networks initialized with a prior that selects for suitably abstract features that maximize executive performance.
The global workspace enables us to construct and maintain a complex composite representation in a serial fashion guided by attention. This can be accomplished using a form of persistent memory enabled by fast weights — originally referred to as dynamic links in the work of Christoph von der Malsburg — to manage a working memory in which information can be added, modified and removed, that supports associative retrieval and is implemented as a fully differentiable model and so can be trained end-to-end by gradient descent. Fast weights are used to store temporary memories of the recent past and provide a neurally plausible method of implementing the type of attention to the past that has recently proved helpful in sequence-to-sequence models. In Section IGNORE, we study how this capability plays a key role in long-term / episodic memory.
You can think of the episodic memory encoded in the hippocampus and entorhinal cortex as RAM and the actively maintained memories in the prefrontal cortex as the contents of registers in a conventional von Neumann architecture. Since the activated memories have different temporal characteristics and functional relationships with the contents of the global workspace, we implement them as two separate NTM memory systems each with its own special-purpose controller.
The cortical sheet, in addition to its layered structure, appears to be tiled with columnar structures referred to as cortical columns. Some neuroscientists believe that all of these columns compute the same basic function. However, there is considerable variation in cell type, thickness of the cortical layers, and the size of the dendritic arbors to question this hypothesis. The prefrontal cortex is populated with a type of neuron, called a spindle neuron, similar in some respects to the pyramidal cells found throughout the cortex, that allow rapid communication across the large brains of great apes, elephants, and cetaceans. Although rare in comparison to other neurons, spindle neurons are abundant and quite large in humans and apparently play an important role in consciousness and attentional networks.
These attentional networks are connected to regions throughout the cortex and are trained via reinforcement learning to recognize events worth attending to according to the learned value function. Using extensive networks of connections — both incoming and outgoing, attentional networks are able to create a composite representation of the current situation that can serve a wide range of executive cognitive functions, including decision making and imagining possible futures. The basic idea of a neural network trained to attend to relevant parts of the input is key to a number of the systems that we'll be looking at.
2.11 Machine Memory Models
In the artificial neural networks discussed in the previous chapter, short-term memories reside for seconds in the transient activation patterns of the units in hidden layers and for longer — indefinitely if actively maintained — in the case of recurrent networks. Long term memories are encoded in the connection-weight matrices of each layer as a result of batch training with stochastic gradient descent.
In this chapter, we discuss artificial neural network components that borrow from both biological and conventional computing technologies. These hybrid memory architectures have homologous structures in biological systems. However, they were not designed for the purpose and hence are ill-suited to many of the tasks we attempt to apply them to, e.g., remembering lists of more than a few words or doing long division in your head [48].
This section is about machine models of memory. However, this book is about how our understanding of the human brain has informed our efforts to build artificial brains and so, here, following up on the example presented in Section IGNORE, we introduce the second of our two examples illustrating how our study of biological neural networks has guided us in designing artificial neural networks. This example involves our ability to encode vivid memories of our experience and recall specific memories that help us to imagine alternative futures to solve our immediate problems and plan for the future.
Episodic Memory
Figure 11 provides a glimpse of how we construct memories of our experience and subsequently retrieve those memories to support a diverse range of cognitive strategies. In this case, the hypothalamus will play a central role as did the basal ganglia in the previous example. Later in this book we explore how the basal ganglia work in concert with the hypothalamus to support reinforcement learning. For now, our goal is simply to describe the process whereby we consolidate and then encode experience. In doing so we will also take the opportunity to talk about the process whereby we retrieve memories, reconstruct a version of that past experience to perform counterfactual inference and imagine possibilities that we have never actually experienced.
| |
| Figure 11: The left panel depicts ... The right panel ... See here for links to relevant 2018 class lectures, related papers and educational animations. | |
|
|
The name hippocampus like so many biological terms has obscure origins, generally in Latin or Greek and in this case the latter, relating to its shape that looked like a seahorse to some early anatomists. As shown in Figure 11.A it is primarily comprised of four subnuclei referred to as CA1, CA2, CA3 and CA4, the first two characters in each abbreviation recalling a previous Latin name, Cornu Ammanonis associated with a ram's horn, apparently preferred by even earlier anatomists. These nuclei are capped by the dentate gyrus (DG) at one end and the fornix at the other80.
The hippocampus consists of two nearly identical structures, one in each hemisphere, connected where the parallel tracts of the fornix come together at the midline of the brain. The hippocampus is tightly coupled with the entorhinal cortex (EHC) that plays an important role in memory, navigation and our perception of time. Information flows from the EHC to the hippocampus by one of two pathways: either through the DG to CA3 or via reciprocal connections to and from CA1. The EHC also has reciprocal connections to many cortical areas81.
In the process of creating a new memory, the hippocampus receives input from multiple cortical areas relevant to current experience, consolidates this information in a condensed format that will enable subsequent retrieval and stores the resulting encoding in memory. In retrieving an existing memory, The EHC starts with cortical activity, typically from motor and sensory association areas, and uses this information to reconstruct a previous memory by activating cortical areas corresponding to the original memory. Before describing how we think such creative consolidation and subsequent reconstruction works, a word about why this process is beneficial might be in order.
Almost every stage of memory is fraught with opportunities to distort the truth. Reconstruction is a creative process in which we are more often than not forced to fill in some details that we might think we observed at the time but actually didn't. In the formation of new memories, consolidation can only make do with whatever information about the experience we have gleaned from observation and committed to short-term memory. If you don't rehearse what you've stored in short-term memory then it will quickly fade, losing detail and potentially introducing errors of omission and commission.
You might purposely or unconsciously alter what you think you remember to conveniently leave the impression that you behaved better than you actually did. There are all kinds of reasons to alter your memories to suit your purposes just as there all sorts of reasons for lying to ourselves [125]. Self-deception can offer interpersonal benefits that offset its costs in whatever currency you value most. There is evidence to suggest that people lie to convince themselves of the truth of their persuasive goal, and by doing so, are able to argue their case more persuasively to others [115].
This sort of imaginative reconstruction has called into question the accuracy of first-person accounts and expert witnesses. But it also explains our eminently useful commonsense application of believable counterfactual reasoning, e.g., if I hadn't had that second cup of coffee, I would have slept better last night [94, 26]. And, considered in the context of avoiding dangerous situations, planning for contingencies, or imagining a world very different from the one in which we live, one that can inspire and motivate us to act to achieve such a future, it underscores the amazing strength, resilience and determination of the human mind.
The basic mechanism employed by the hippocampus and entorhinal cortex working together is illustrated in Figure 11.B. There are two basic processes that we consider here: encoding new memories and retrieving of old memories. Encoding involves collecting information gleaned from diverse neural activity originating in multiple cortical regions and consolidating [82] this information to construct a compact encoding that serves as a key or index that will enable subsequent stable — meaning reliably consistent even in the presence of distracting information [36] — retrieval and reconstruction82.
EHC receives input from all cortical regions in a condensed form and the axons of EHC pyramidal neurons project primarily to the DG but also to CA1. DG then projects to CA3 which plays a particularly important role in encoding and retrieving memories. CA3 is thought to behave as an autoassociative memory shown here as a recursive neural network. The crucial property of an autoassociative memory is that it is able to retrieve an item from memory using only a portion of the information associated with that item83.
For example, this property allows us to retrieve information about a party that was held years ago just by catching a glimpse of a person on the street who happens to look like someone whom we first met at that party. You can think of your observation of the person from the party as a probe or key that enables you to access and unlock that earlier experience. Of course, you could have simply mistaken that person you saw on the street for the person you met at the party.
Hippocampal indexing theory [123] hypothesizes that when we have a conscious experience, different areas of the cortex are activated related to that experience such as activity in the auditory cortex resulting from our listening to a recording of Yo-Yo Ma playing Bach or activity in the visual cortex produced by a particularly vivid sunset we witnessing. When we remember the experience later, similar areas of the cortex are reactivated allowing us to re-experience the event.
The hippocampus serves as an index, storing different patterns of neocortex activity and allowing us to retrieve our memories using only a fragment of what we can recall. The recurrent connections of CA3 are thought to enable this sort of creative reconstruction and play a role in both encoding and retrieving memories. CA3 then projects to CA1 and from there back to the EHC completing the loop and thereby providing recurrent activity involving a much larger circuit.
There are a couple of details that are worth pointing out here as they demonstrate both the strengths and weaknesses of human episodic memory. The first concerns the issue of retrieving a complete memory given a partial index and the second concerns how to retrieve a memory when that memory is similar to one or more other memories, at least in the sense that their respective indices are similar to one another. In the model described here, the first issue is handled by the autoassociative network.
| |
| Figure 12: The three panels shown here represent the autoassociative network representing the function of CA3 in the hippocampus. Connection weights are shown as diagonal lines, e.g., the dotted blue lines shown in the network on the far left represent the connection weights prior to any training. The middle panel represents the network after encoding the stimulus pattern corresponding to the cortical activation of A and C, and the panel on the far right represents the network, when presented with a partial pattern consisting of just C, employing the recurrent connections of the autoassociator to complete the pattern for the original stimulus and using it to reconstruct the corresponding activation of A and C in the cortex. | |
|
|
The triptych shown in Figure 12 illustrates how the autoassociative network solves this problem. The panel on the far left is meant to indicate the autoassociative network and its initial state. In the middle panel, we assume the input from the dentate gyrus consist of the two sub patterns A and C and illustrates the reciprocal connections that would be strengthened were we to train the network with this composite pattern of activity. CA3 is responsible for encoding these memory specific patterns of activity for all of our memories. The panel on the far right is intended to illustrate how given a partial pattern, in this case just one of the two representative patterns that comprise the composite pattern shown in the middle panel, is able to reconstruct the other representative pattern by using the trained autoassociative network to first identify and then strengthen the connections in the original composite.
The second detail concerns the possibility that the encodings for two memories are alike enough to be mistaken with one another. A full account of any of the theories explaining how the human brain solves this problem is beyond the scope of what we can go into here but one theory — first articulated by David Marr [73, 139] — posits that, since the dentate gyrus has a larger number of cells than the EHC, its forward projection will tend to produces an expansion recoding in the DG leading to an increase in the separation between the patterns in CA3. Evidence from recordings in mice and computational modeling using artificial neural network and dynamical system models offer support for the theory [88].
To complete our account of memory retrieval, we look at how the path that started in the EHC loops back to complete a feedback loop that stabilizes the encoding of memories. So far we've seen how an experience represented by a pattern of activations in the cortex is compressed and represented in the entorhinal cortex which projects this pattern onto the cells in the dentate gyrus thereby increasing the separation between competing patterns the results of which are bound together to generate an index. This index is fed to CA3 where it is incorporated in an autoassociative recursive network so that subsequently when a feature of the original stimulus is present in our conscious experience it activates a subset of the original neurons activated in CA3 and the recurrent connections in the autoassociative network reactivate the remaining neurons completing the pattern that was incorporated when the experience was initially encoded in memory.
The remaining step involves explaining how the representation in CA3 reactivates the original stimulus. As shown in Figure 11.B, the entorhinal cortex projects to CA1 in addition to the dentate gyrus. When neurons are projected forward to DG and activated in CA3 they are also activated in CA. Since they are activated at the same time, the connections between the neurons in CA3 and CA1 are strengthened by long-term potentiation84. The result is a stable, sparse, invertible mapping that allows the hippocampus to recreate the original cortical activity patterns during retrieval [92, 78]. Reactivating the same combination of cortical areas as the original stimulus and causing us to reexperience the event as a memory. While still speculative, an additional process called reconsolidation is thought to allow previously-consolidated memories become labile again as a consequence of reactivation85.
Neural Turing Machines
| |
| Figure 13: This figure illustrates Neural Turing Machine (NTM) model also known as Differentiable Neural Computer (DNC). Shown here is graphic we'll use to signify an NTM as a component in a larger neural network with the only difference being that (A) represents a relatively small, fixed-size memory and (B) represents an extensible, arbitrarily large memory with multiple read and write heads supporting optimized parallel reads and writes. | |
|
|
For the most part, human memory and the artificial neural networks developed to emulate human cognition are based on the sort of distributed representations that are the hallmark of connectionist models. This sort of memory has a number of characteristics that complement the sort of memory employed in conventional computing hardware and software. Memory in connectionist models is contextual in terms of how it encodes meaning and fluid in terms of allowing us to represent concepts with flexible, semi-permeable boundaries. Memory in conventional computing hardware is said to be compositional — complex representations can be composed of other complex representations or simpler ones and these compositions behave in a straightforward manner in terms of not altering the meaning of the constituents — and systematic — exhibit a clear separation between form and content / syntax and semantics86.
Conventional computing is well suited to maniplating symbolic representations such as word sequences, documents and highly structured data such as labeled graphs and tables with named rows and columns. Conventional computing technologies include high-performance hardware for calculations involving logic and mathematics, and high-capacity memory supporting low-latency reads and writes. Conventional and connectionist computing models complement one another, and, while humans are able to perform symbolic reasoning by essentially simulating it on a connectionist architecture, the inference is slow and error-prone. To compensate, neural network researchers have developed hybrid computing models that provide the benefits of conventional computing models, by employing differentiable interfaces compatible with connectionist architectures that can be trained to serve different purposes.
Neural Turing Machines (NTM) — also known as Differentiable Neural Computers (DNC) — can be added to connectionist models to provide conventional computing and memory services [48, 47]. Here we describe one such component supporting content-addressable random-access key-value memory. In a traditional key-value memory, entries are stored in a table as pairs (key, value). To add a new entry you simply insert a new entry in the table, if there already exists an entry with the same key, then the system either signals an error or updates the value in the existing entry. To look up a value given a query key you simply find the corresponding entry and return the value or signal an error if there is no entry with the given key. This is not quite the same as conventional random access memory (RAM) since the keys need not be ordered in memory as they are in conventional RAM using sequential binary addresses.
The keys in a conventional key-value memory are typically strings, symbols or integers, none which is much use in a connectionist model. As one might expect, DNC keys and values correspond to activation patterns in network layers and so are realized as vectors of real numbers. Considered as a function that given a key returns a value, traditional key-value memory is not differentiable and hence the corresponding DNC interface function can't be learned by an artificial neural network. First of all, given that the keys are real valued vectors the probability that exactly the same vector will be computed and used as a key is vanishingly small. We can compensate for this by finding the entry with the key closest to the query key, where by closest we mean the closest in the corresponding vector space typically determined by the obvious \({n}\)-dimensional generalization of the Euclidean distance metric.
Unfortunately picking the entry with the closest key is still a non-differentiable function, since given a small change in the query key the corresponding closest entry could change, resulting in a discontinuous change in the value returned by the function. To remedy this problem, we use the same trick that we employed in the previous chapter by using the continuous softmax function as an alternative to the conventional discontinuous max function. What this means in the case of a differentiable key-value memory, is that we compute the distance from the query key to each key corresponding to an entry in memory, we then normalize the distances so that each normalized distance is a number between 0 and 1 and together they sum to 1, resulting in a vector we can interpret as a probability distribution. Finally, we compute the weighted sum of all the values in the entries stored in the memory, where the weights correspond to the normalized distances.
The keys and values are all generated by the neural network implementing the target application. Exactly how the keys and values are distributed in their corresponding vector spaces is largely determined by the objective function and the training data. Recall from the previous chapter that each layer constitutes a separate vector space and the learned weight matrix associated with the connections between adjacent layers composed with the corresponding activation function defines a transformation from one vector space to another. The only model parameters that serve to influence the associated vector spaces are those that determine the number of units in each layer and so the dimensionality of each vector space. The dictates of the problem — implicit in the objective function and the training data — will determine how the values are distributed in the corresponding vector spaces.
The vectors corresponding to the activation patterns in a given layer could be sparsely distributed and hence well separated and unlikely to be confused with one another, or they could be clumped with each clump corresponding to some class of roughly similar vectors. The keys will have their related distributional characteristics. The point is that these distributions will be shaped by the objective function and the data and so we don't have to constrain them any further — indeed we would be foolish to try to second guess training. The original paper describing the DNC model notes that their model exhibits usage patterns that exhibit parallels between the DNC and mammalian hippocampus87, and we explore this connection in Section IGNORE on the neural correlates of episodic memory.
The learnable weights that govern the behavior of a DNC model are organized in a controller module illustrated in Figure 13. The models shown in (A) and (B) have essentially the same controller but differ in terms of the conventional memory component. The model labeled (A) has a fixed-size memory of the sort you might find in a microprocessor central processing unit (CPU) consisting of a set of registers used to temporarily store operands when executing machine instructions. The model labeled (B) has an arbitrarily large memory such as that provided by a conventional electromechanical hard disk drive or solid-state RAM disk. The controller uses three differentiable attention networks to define distributions over the \({N}\) rows or locations in the \({N \times{} W}\) memory matrix \({M}\).
The attention networks are used to generate location addresses to control a read head and a write head borrowing from the terminology of conventional disk drives. For some applications, a DNC model can be configured to operate multiple read and write heads to facilitate parallel reads and writes. The first attention network assists with content addressing for reads and writes by using the method described earlier in which reads and writes are distributed over multiple locations depending on their similarity to the key vector emitted by the controller. The second attention network assists in traversing consecutively written locations and the third allocates memory locations for writing. Together these three attention networks plus controller provide a versatile alternative to using recurrent networks for maintaining state information.
Episodic Memory
Fundamental to our understanding of human cognition is the essential tradeoff between fast, highly-parallel, context-sensitive, distributed connectionist-style computations and slow, serial, systematic, combinatorial symbolic computations. In developing the programmer's apprentice, symbolic computations of the sort common in conventional computing are realized using extensions that provide a differentiable interface to conventional memory and information processing hardware and software. Such interfaces include the Neural Turing Machine [47] (NTM), Memory Network Model [138, 116] and Differentiable Neural Computer [48] (DNC).
The global workspace summarizes recent experience in terms of sensory input, its integration, abstraction and inferred relevance to the context in which the underlying information was acquired. To exploit the knowledge encapsulated in such experience, the apprentice must identify and make available relevant experience. The apprentice’s experiential knowledge is encoded as tuples in a Neural Turing Machine (NTM) memory that supports associative recall. We’ll ignore the details of the encoding process to focus on how episodic memory is organized, searched and applied to solving problems.
In the biological analog of an NTM the hippocampus and entorhinal region of the frontal cortex play the role of episodic memory and several subcortical circuits including the basal ganglia comprise the controller [91, 89]. The controller employs associative keys in the form of low-dimensional vectors generated from activations highlighted in the global workspace to access related memories that are then actively maintained in the prefrontal cortex and serve to bias processing throughout the brain but particularly in those circuits highlighted in the global workspace. Figure 14 provides a sketch of how this is accomplished in the apprentice architecture.
| |
| Figure 14: You can think of the episodic memory encoded in the hippocampus and entorhinal cortex as RAM and the actively maintained memories in the prefrontal cortex as the contents of registers in a conventional von Neumann architecture. Since the activated memories have different temporal characteristics and functional relationships with the contents of the global workspace, we implement them as two separate NTM memory systems each with its own special-purpose controller. Actively maintained information highlighted in the global workspace is used to generate keys for retrieving relevant memories that augment the highlighted activations. In the DNC paper [48] appearing in Nature, the authors point out that "an associative key that only partially matches the content of a memory location can still be used to attend strongly to that location [allowing] allowing the content of one address [to] effectively encode references to other addresses". The contents of memory consist of thought vectors that can be composed with other thought vectors to shape the global context for interpretation. | |
|
|
Figure 15 combines the components that we've introduced so far in a single neural network architecture. The empty box on the far right includes both the language processing and dialogue management systems as well the networks that interface with FIDE and the other components involved in code synthesis. There are several classes of programming tasks that we might tackle in order to show off the apprentice, including commenting, extending, refactoring and repairing programs. We could focus on functional languages like Scheme or Haskell, strongly typed languages like Pascal and Java or domain specific languages like HTML or SQL.
However, rather than emphasize any particular programming language or task, in the remainder of this appendix we focus on how one might represent structured programs consisting of one or more procedures in a distributed connectionist framework so as to exploit the advantages of this computational paradigm. We believe the highly-parallel, contextual, connectionist computations that dominate in human information processing will complement the primarily-serial, combinatorial, symbolic computations that characterize conventional information processing and will have a considerable positive impact on the development of practical automatic programming methods.
| |
| Figure 15: This slide summarizes the architectural components introduced so far in a single model. Data in the form of text transcriptions of ongoing dialogue, source code and related documentation and output from the integrated development environment are the primary input to the system and are handled by relatively standard neural network models. The Q-network for the attentional RL system is realized as a multi-layer convolutional network. The two DNC controllers are straightforward variations on existing network models with a second controller responsible for maintaining a priority queue encodings of relevant past experience retrieved from episodic memory. The nondescript box labeled "motor cortex" serves as a placeholder for the neural networks responsible for managing dialogue and handling tasks related to programming and code synthesis. | |
|
|
2.12 Embodied Cognition
There is a very real sense in which the apprentice is embodied in the same sense the Deep Recurrent Attentive Writer neural network architecture — the acronym is DRAW — developed by researchers at DeepMind embodies a digital slate and drawing program. DRAW networks employ a spatial attention mechanism that mimics foveation of the human eye, allowing it to iteratively construct complex images. The browser interface serves as a special type of prostheses enabling the assistant to interface more directly with the programmer by directly apprehending every key stroke and mouse movement initiated by the programmer.
The most efficient mode of interaction between the apprentice and programmer is likely to be through the use of natural language. Existing personal assistants are not particularly talented at continuous dialogue. The job of the apprentice is simplified somewhat by the relatively narrow scope of the task of programming. That said, verbal communication is complicated by the inherent ambiguity of natural language, the importance of reading another person's body language and facial cues, the subtlety required to notice when our conversational partner is confused and then easily recover from misunderstanding, and, finally, the fact that human beings share a great deal of basic knowledge and common sense.
We imagine the programmer's apprentice with a body part consisting of an instrumented integrated development environment (IDE). Alternatively you might think of it as a prosthetic device. It is not, however, something that you can simply remove or replace with an alternative device outfitted with a different interface or supporting different functions. Like the legs you were born with or the prosthesis replacing an amputee's severed arm, you have to learn how to use these devices.
Architecturally, the apprentice's prosthetic IDE is an instance of a differentiable neural computer (DNC) introduced by Alex Graves and his colleagues at DeepMind. The assistant combined with its prosthetic IDE is neural network that can read from and write to an external memory matrix, combining the characteristics of a random-access memory and set of memory-mapped device drivers and programmable interrupt controllers. The interface supports a fixed number of commands and channels that provide feedback. You can think of it as roughly similar to an Atari game console.
| |
| Figure 16: Graphic rendering of Wilder Penfield's topographical maps of the sensory and motor cortices of the brain showing their connections to the various limbs and organs of the body. Often referred to cortical homunculi, these graphical overlays of the motor and somatosensory areas in the parietal lobe map regions of cortex to parts of the body so that the size of the distorted body part as drawn roughly accounts for the amount of cortical tissue dedicated to that part. This dedicated tissue can grow or shrink depending on its use. Professional pianists show increases in those areas of the somatosensory cortex relating to the hands when compared with the norm [43]. | |
|
|
The spatial relationships among the ganglion cells in the retina are preserved in the activity of neurons found in the primary visual — or striate — cortex. Most sensory and motor areas maintain similar modality-specific topographic relationships. Shown here, for example, are Wilder Penfield's famous motor and somatosensory homunculi depicting the areas and proportions of the human brain dedicated to processing motor and sensory functions. Scientists have observed that the area devoted to the hands tend to be larger among pianists, while the relevant areas in the brains of amputees typically become significantly smaller.
In the mammalian brain, information pertaining to sensing and motor control is topographically mapped to reflect the intrinsic structure of that information required for interpretation. This was early recognized in the work of Hubel and Wiesel on the visual cortex and Wilder Penfield in his work developing the notion of a cortical homunculus in the primary motor and somatosensory areas of the cortex as shown here. Such maps relate to the idea of embodied intelligence.
The integrated development environment and its associated software engineering tools constitute an extension of the apprentice’s capabilities in much the same way that a piano or violin extends a musician. The extension becomes an integral part of the person possessing it and over time their brain creates a topographic map that facilitates interacting with the extension.
As engineers designing the apprentice, part of our job is to create tools that enable the apprentice to learn its trade and eventually become an expert. Conventional, IDE tools simplify the job of software engineers in designing software. The IDE that we build for the apprentice (FIDE) will be integrated into the apprentice’s cognitive architecture so that tasks like stepping a debugger or setting breakpoints are as easy for the apprentice as balancing parentheses and checking for spelling errors in a text editor is for us.
Procedure Model
The integrated development environment and its associated software engineering tools constitute an extension of the apprentice’s capabilities in much the same way that a piano or violin extends a musician or a prosthetic limb extends someone who has lost an arm or leg. The extension becomes an integral part of the person possessing it and over time their brain creates a topographic map that facilitates interacting with the extension88.
As engineers designing the apprentice, part of our job is to create tools that enable the apprentice to learn its trade and eventually become an expert. Conventional IDE tools simplify the job of software engineers in designing software. The fully instrumented IDE (FIDE) that we engineer for the apprentice will be integrated into the apprentice’s cognitive architecture so that tasks like stepping a debugger or setting breakpoints are as easy for the apprentice as balancing parentheses and checking for spelling errors in a text editor is for us.
As a first step in simplifying the use of FIDE for coding, the apprentice is designed to manipulate programs as abstract syntax trees (AST) and easily move back and forth between the AST representation and the original source code in collaborating with the programmer. Both the apprentice and the programmer can modify or make references to text appearing in the FIDE window by pointing to items or highlighting regions of the source code. The text and AST versions of the programs represented in the FIDE are automatically synchronized so that the program under development is forced to adhere to certain syntactic invariants.
| |
| Figure 17: We use pointers to represent programs as abstract syntax trees and partition the NTM memory, as in a conventional computer, into program memory and a LIFO execution (call) stack to support recursion and reentrant procedure invocations, including call frames for return addresses, local variable values and related parameters. The NTM controller manages the program counter and LIFO call stack to simulate the execution of programs stored in program memory. Program statements are represented as embedding vectors and the system learns to evaluate these representations in order to generate intermediate results that are also embeddings. It is a simple matter to execute the corresponding code in the FIDE and incorporate any of the results as features in embeddings. | |
|
|
To support this hypothesis, we are developing distributed representations for programs that enable the apprentice to efficiently search for solutions to programming problems by allowing the apprentice to easily move back and forth between the two paradigms, exploiting both conventional approaches to program synthesis and recent work on machine learning and inference in artificial neural networks. Neural Turing Machines coupled with reinforcement learning are capable of learning simple programs. We are interested in representing structured programs expressed in modern programming languages. Our approach is to alter the NTM controller and impose additional structure on the NTM memory designed to support procedural abstraction.
Execution Model
What could we do with such a representation? It is important to understand why we don’t work with some intermediate representation like bytecodes. By working in the target programming language, we can take advantage of both the abstractions afforded by the language and the expert knowledge of the programmer about how to exploit those abstractions. The apprentice is bootstrapped with several statistical language models: one trained on a natural language corpus and the other on a large code repository. Using these resources and the means of representing and manipulating program embeddings, we intend to train the apprentice to predict the next expression in a partially constructed program by using a variant of imagination-based planning [95]. As another example, we will attempt to leverage NLP methods to generate proposals for substituting one program fragment for another as the basis for code completion.
| |
| Figure 18: This slide illustrates how we make use of input / output pairs as program invariants to narrow search for the next statement in the evolving target program. At any given moment the call stack contains the trace of a single conditioned path through the developing program. A single path is unlikely to provide sufficient information to account for the constraints implicit in all of the sample input / output pairs and so we intend to use a limited lookahead planning system to sample multiple execution traces in order to inform the prediction of the next program statement. These so-called imagination-augmented agents implement a novel architecture for reinforcement learning that balances exploration and exploitation using imperfect models to generate trajectories from some initial state using actions sampled from a rollout policy [95, 137, 52, 51]. These trajectories are then combined and fed to an output policy along with the action proposed by a model-free policy to make better decisions. There are related reinforcement learning architectures that perform Monte Carlo Markov chain search to apply and collect the constraints from multiple input / output pairs. | |
|
|
The Differentiable Neural Program (DNP) representation and associated NTM controller for managing the call stack and single-stepping through such programs allow us to exploit the advantages of distributed vector representations to predict the next statement in a program under construction. This model makes it easy to take advantage of supplied natural language descriptions and example input / output pairs plus incorporate semantic information in the form of execution traces generated by utilizing the FIDE to evaluate each statement and encoding information about local variables on the stack.
Embodied Brains
There are science fiction books and movies about brains separated from bodies that are artificially kept alive and are able to interact with the world through various brain-computer interfaces. The interfaces allow these disembodied brains to apprehend what's going on around them and possibly control robotic arms to touch, feel and manipulate physical objects. There are also patients with a medical condition called locked in syndrome resulting from a stroke that damages part of the brain stem so that the body, including most of the facial muscles, is paralyzed but consciousness remains and the ability to perform certain eye movements is preserved.
It is hard to imagine what it would be like not to have a body or to have a body but not feel it. The fictional accounts of brains without bodies give the impression that, assuming form of advanced medicine, brains could carry on quite happily relieved of their bodies. There is no insurmountable technical barrier to keeping a brain alive on life support indefinitely. However the human body and brain are so interdependent that to have never experienced what it's like to have one would result in our being as much different from other humans as naturally embodied humans are different from dolphins, whales, elephants or any other intelligent species.
The physical basis that determines how we think extends well beyond the central nervous system. What you see, hear and feel, the way in which you express yourself, how you deal with challenging situations and relate to others are inextricably dependent on the many chemical, electrical and genomic pathways that govern how you feel and filter what you perceive. Your interaction with other others is largely determined by factors beyond your control including not only your behavior and current physical state but a much larger ensemble of social and emotional factors that create the context for everything that you experience [66, 128].
One important consequence of how your body and the environment that you inhabit influence your thinking is that your experience serves to ground your use of language. The meaning of visual signs and spoken words are determined by what they refer to or signify. While you can introduce several steps of indirection, eventually signs and words are grounded in experience and the richer that experience the richer your repertoire of analogies, abstractions, relationships, etc. Being able to ground concepts in a physically coherent reality allows you to draw upon your experience to check what you think against a ruthlessly honest account of what is really possible.
This ability to test our naïve theories against the physics of the real world provides a self-correcting feedback loop — a recurrent process that feeds back on itself. The system composed of the brain, body and environment is common in nature and fundamental in the field of cybernetics — the study of communication and control in animals and machines. Human beings routinely extend their reach by creating self-consistent physical systems as well as abstract theoretical systems governed by the uncompromising laws of logic and mathematics. Human language is permeated with analogies that provide additional means for extending and checking our theories.
The same principle applies in communication. Dialogue is not a sequence of unrelated utterances, but rather it is a collaborative act in which speaker and hearer must constantly establish common ground to make it clear that the hearer has understood the speaker's meaning and intention89 . This is challenging when speaker and hearer have different grounding but made possible through analogy. The programmer tells the assistant that he has to use the toilet. Puzzled, the assistant asks, "What is a toilet?" After some tortured back and forth, the assistant proudly says, "That's like when my program uses up all the available memory and I have to run my garbage collection routine to free up some space."
Einstein grounded his nascent theory of light and gravity in terms of trains traveling along parallel tracks. He had to make leap beyond his physical experience, but thinking about trains provided a vantage point from which it was possible to make the leap to curved spacetime. Our experience of physically interacting with the world around us provides us a system we can use to draw commonsense conclusions about the physics that governs our world. If two people inhabit very different environments they can share their experience through analogy. Language is the most powerful technology humans invented and, while language is not necessary to survive, it enables us to rise above mere existence.
The programmer's assistant lacks a physical body but is immersed in several engineered systems having their own internal consistency and sources of inspiration. First of all, the assistant is constantly engaged in conversation with the programmer with whom it shares the context of their joint efforts to produce software. In addition, the assistant lives in a world of code (software) and computing hardware. The assistant can think and communicate in programming language, execute lines of code as you would swat a fly or scratch an itch and interact directly with running code as though the hardware and the programming tools that run on the hardware are natural extensions of its mind.
As engineers designing the apprentice, part of our job is to create tools that enable the apprentice to learn its trade and eventually become an expert. Conventional integrated development environment (IDE) tools simplify the job of software engineers in designing software. The fully instrumented IDE (FIDE) that we engineer for the apprentice is integrated into the apprentice's cognitive architecture so that tasks like stepping a program in a debugger or setting breakpoints are as easy for the apprentice as balancing parentheses and checking for spelling errors in a text editor is for us. The FIDE is both cognitive prosthesis and gateway into a world the assistant inhabits.
2.13 Planning and Behaving
The basal ganglia in cognitive models such as the one described by Randall O'Reilly's in his presentation in class, play a central role in action selection. This seems like a good opportunity to review how actions are represented in deep-neural-network implementations of reinforcement learning. Returning to our default representation for the simplest sort of episodic memory, \({(s_{t}, a_{t}, r_{t}, s_{t+1})}\), it’s easy to think of a state \({s}\) as a vector \({s \in{} \mathbf{R}^{n}}\) and a reward \({r}\) as a scalar value, \({r \in{} \mathbf{R}}\), but how are actions represented?
Most approaches to deep reinforcement learning employ a tabular model of the policy implying a finite — and generally rather small — repertoire of actions. For example, most of the experiments described in Wayne et al [136] (MERLIN) six-dimensional one-hot binary vector that maps a set of six actions: move forward, move backward, rotate left with rotation rate of 30, rotate right with rotation rate of 30, move forward and turn left, move forward and turn right. The action space for the grid-world problems described in Rabinowitz et al [101] (ToMnets) consists of four movement actions: up, down, left, right and stay.
Rather than immediately focusing on how biological and artificial brains learn and apply hierarchical models, we start by considering the simpler problem of how we might represent a subroutine, the smallest fungible unit of activity for our purposes. Subroutines can be used to kick a soccer ball or implement simple program transformations in a neural-network architecture.
We begin with the simplifying assumption that subroutines can be represented as tuples consisting of a set of operands represented as high-dimensional embedding vectors, a weight matrix representing the transformation and a product vector space in which to embed the result. ... arbitrary source code is unwieldy and designed for the convenience of someone writing code ... an abstract syntax tree (AST) is alternative canonical representation for representing the abstract syntactic structure of a source-code program90 [35, 135] in a manner that is more convenient for computer program to manipulate ... In applying this idea to program transformations, assume that each operand corresponds to the embedding of an abstract-syntax-tree representation of a code fragment, w.l.o.g., any non-terminal node in the AST of a syntactically well-formed program.
The programmer's apprentice operates on programs represented as trees, where the set of actions includes basic operations for traversing and editing trees — or more generally directed-graphs with cycles if you assume edges in abstract syntax trees corresponding to loops, recursion and nested procedure calls, i.e., features common to nearly all the programs we actually care about. We still have a finite number of actions since for any given project we can represent the code base as a directed-acyclic graph with annotations to accommodate procedure calls and recursion, and use attention to direct and contextualize a finite set of edit operations91.
In a collaboration, figuring out what to say requires planning and a certain degree of imagination. Suppose you are the apprentice and you want to tell the programmer with whom you're collaborating that you don't understand what a particular expression does. You want to understand what role it plays in the program you are jointly working on. How do you convey this message? What do you need to say explicitly and what can be assumed common knowledge? What does the programmer know and what does she need to be told in order to provide you with assistance?
Somehow you need to model what the programmer knows. In planning what to say, you might turn this around and imagine that you're the programmer and ask how you would respond to an apprentice's effort to solicit help, but in imagining this role reversal you have be careful that you don't assume the programmer knows everything that you do. You need a model of what you know as well as a model of what the programmer knows. This is called Theory of Mind (ToM) reasoning and learning how to carry out such reasoning occurs in a critical stage of child development.
Shared knowledge includes general knowledge about programming, knowledge about the current state of a particular program you are working on, as well as specific details concerning what you are attending to at the moment, including program fragments and variable names that have been mentioned recently in the discussion or can be inferred from context. This sort of reasoning can be applied recursively if, for example, the apprentice wants to know what the programmer thinks it knows about what the apprentice knows. To a large extent we can finesse the problem of reasoning about other minds by practicing transparency, redundancy and simplicity so that both parties can depend on not having to work hard to figure out what the other means. However, there are some opportunities in the programmer's apprentice problem for applying ToM reasoning to parts of the problem that cannot be so easily finessed.
Suppose that the apprentice has started a new program using an existing program P following a suggestion by the expert programmer. Realizing that the body of a loop in P is irrelevant to the task at hand, the apprentice replaces the useless body B with a fragment from another program that does more or less what is required and then makes local changes to the fragment to create a new body B′ so that it works with the extant loop variables, e.g., loop counter, termination flag, etc. When the assistant has completed these local changes, the programmer intervenes and changes the name of a variable in B′. What induced the programmer to make this change?
The programmer noticed that the variable in B′ was not initialized or referenced in P but that another variable that was initialized in P and is no longer referenced — it only appeared in the original loop body B, is perfectly suited for the purposes of the new program. Assume for the sake of this discussion, that the programmer does not explain her action. How might the assistant learn from this intervention or, at the very least, understand why it was made? A reasonable theory of mind might assume that agents perform actions for reasons and those reasons often have to do with preconditions for acting in the world, and, moreover, that determining if action-enabling preconditions are true often requires effort. A useful ToM also depends on having a model allowing an agent to infer how preconditions enable actions by working backward from actions to enabling preconditions.
The phrase "Theory of Mind" refers to the idea that humans and possibly other organisms construct models of how other agents reason in order to understand and anticipate the behavior of such agents. Developmental psychologists have conducted fascinating research about how and when children learn such models, and what goes wrong when children fail to learn such models during a crucial developmental window.
Theory of Mind Reasoning refers to the mental processing required to employ such models in various collaborative and strategic circumstances. Here we consider what it would mean for a machine to learn such a theory and employ it in practical applications such as the programmer's apprentice. I've left this topic for last for a number of reasons. It might seem presumptive to suppose that machines could learn such models. It might not at first blush appear to be useful, but on reflection I hope you will agree that when two programmers collaborate in designing or debugging a computer program, it helps a lot to have some idea of what the other programmer knows or might be mistaken about.
Imagine the following scene, there's a man holding the reins of a donkey harnessed to a two-wheeled cart — often called a dray and its owner referred to as a drayman — carrying a load of rocks. He makes the donkey rear up and by so doing the surface of the cart tilts, dumping the rocks onto the road which was clearly his intention given the appreciative nods from the onlooking pedestrians. This short video illustrates that, while this might seem an unusual way of delivering a load of rocks, most people think they understand exactly how it was done. Not so!
The fact is that, as with so many other perceptual and conceptual tasks, people feel strongly that they perceived or understood much more than in fact they did. For example, most people would be hard-pressed to induce a donkey to rear up and, if you asked them to draw the donkey harnessed to the cart with its load of stone, they would very likely misrepresent the geometric relationships involving the height of the donkey, how the harness is attached, how far off the ground the axle is located, the diameter of the wheels and the level of the cart surface and center of gravity of the load with respect to the axle's frame of reference. In other words, they would not have — and possibly never could have — designed a working version of the system used by the drayman.
Now imagine that the drayman has a new apprentice who was watching the entire scene with some concentration, anticipating that he might want to do the very same thing before the first week of his apprenticeship is complete. Sure enough, the next day the drayman tells the apprentice to take a load of bricks to a building site in town where they are constructing a chimney on a new house. He stacks the bricks in a pile that looks something like how he remembers the rocks were arranged on the dray the day before. Unfortunately the load isn't balanced over the axle and almost lifts the donkey off its feet. After some experimentation he discovers how to balance the weight so the donkey can pull the load of bricks without too much effort.
When he finally gets to the building site, he nearly gets trampled by the donkey in the process of repeatedly trying to induce the distressed animal to rear up on its hind legs. Finally, one of the brick masons intervenes and demonstrates the trick. Unfortunately, the bricks don’t slide neatly off the dray as the rocks did for the experienced drayman the day before, but instead the bricks on the top of the stack tumble to the pavement and several break into pieces. The helpful brick mason suggests that in the future the assistant should prepare the dray by sprinkling a layer of sand on the surface of cart so that the bricks will slide more freely and that he should also dump the bricks on a softer surface to mitigate possible breakage. He then helps the assistant to unload the rest of the bricks but refuses to pay for the broken ones, telling the assistant he will probably have to pay the drayman to make up for the difference.
An interesting challenge is to develop a model based on what is known about the human brain explaining how memories of the events depicted in the video and extended in the above story might be formed, consolidated, and, subsequently, retrieved, altered, applied and finally assigned a value taking into account the possible negative implications of damaged goods and destroyed property. In the story above, the assistant initially uses his innate "physics engine" to convince himself that he understands the lesson from the master drayman, he then uses a combination of his physical intuitions and trial-and-error to load the cart, but runs up against a wall due to his unfamiliarity with handling reluctant beasts of burden. Finally, he gets into trouble with laws of friction and the quite-reasonable expectations of consumers unwilling to pay for damaged goods.
We don't propose to solve the general problems of theory-of-mind and physics-based reasoning in developing a programmer's apprentice, though the application provides an interesting opportunity to address particular special cases. As mentioned earlier, the stream of conversation between the assistant an expert programmer will inevitably relate to many different topics and specialized areas of expertise. It will include specific and general advice, reasons for acting, suggestions for what to attend to and a wide range of comments and criticisms. Several recent approaches for combining planning and prediction, especially in the case of partially observable Markov decision processes, are particularly promising for this application [50, 39, 41, 136, 114].
The apprentice will want to separate this information into different categories to construct solutions to problems that arise at multiple levels of abstraction and complexity during code synthesis. Or will it? We like to think of knowledge neatly packaged into modules that result in textbooks, courses, monographs, tutorials, etc. The apparent order in which activities appear in a stream of activities is largely a consequence of the context in which those activities are carried out. They may seem to arise in accord with some plan, as if assembled and orchestrated with a particular purpose in mind, but, even if there was plan at the outset, we tend to make up things on the fly to accommodate the sort of unpredictable circumstances that characterize most of our evolutionary history.
In some cases that context or purpose is used to assign a name, but that name or contextual handle is seldom used to initiate or identify the activity except in academic circumstances where divisions and boundaries are highly prized and made much of. The point of this is that in a diverse stream of activities — or utterances intended to instigate activities — credit assignment can be difficult. Proximity in terms of the length of time or number of intervening activities between a action and a reward is not necessarily a good measure of its value. We suggest it is possible to build a programer's apprentice or other sort of digital assistant that performs its essential services primarily by learning to predict actions, their consequences and their value from observing such a diverse stream of dialog intermixed with actions and observations.
Harnessed Imagination
The imagination-based planning (IBP) for reinforcement learning framework [95] serves as an example for how the code synthesis module might be implemented. The IBP architecture combines three separate adaptive components: (a) the CONTROLLER + MEMORY system which maps a state s ∈ S and history h ∈ H to an action a ∈ A; (b) the MANAGER maps a history h ∈ H to a route u ∈ U that determines whether the system performs an action in the COMPUTE environment, e.g., single-step the program in the FIDE, or performs an imagination step, e.g., generates a proposal for modifying the existing code under construction; the IMAGINATION MODEL is a form of dynamical systems model that maps a pair consisting of a state s ∈ S and an action a ∈ A to an imagined next state s′ ∈ S and scalar-valued reward r ∈ R.
The IMAGINATION MODEL is implemented as an interaction network [5] that could also be represented using the graph-networks framework introduced here. The three components are trained by three distinct, concurrent, on-policy training loops. The IBP framework shown in Figure 19 allows code synthesis to alternate between exploiting by modifying and running code, and exploring by using the model to investigate and analyze what would happen if you actually did act. The MANAGER chooses whether to execute a command or predict (imagine) its result and can generate any number of trajectories to produce a tree ht of imagined results. The CONTROLLER takes this tree plus the compiled history and chooses an action (command) to carry out in the FIDE.
| |
| Figure 19: The above graphic illustrates how we might adapt the imagination-based planning (IBP) for reinforcement learning framework [95] for use as the core of the apprentice code synthesis module. Actions in this case correspond to transformations of the program under development. States incorporate the history of the evolving partial program. Imagination consists of exploring sequences of program transformations. | |
|
|
2.14 Language and Thinking
This section is heavily influenced by my reading three books on language all of which take some form of evolutionary stance [24, 122, 34]. Add to that Chomsky, Chater, Deacon and Pinker [20, 16, 27, 98], and you have some idea of the tempest I've ginned up for the purpose of tearing down my outdated conceptions of language and constructing a synthesis that accounts for what I've learned over the last few years92. Is it "ginned up" — enlisting an engine of industrial manufacture, or "jinned up" " — invoking a devil of some demonic species? Perhaps both apply here, but the evolutionary tale of each word is complex as only a linguist could revel in. From my small sample, one might guess that many linguists are channeling the ghosts of William Safire, Samuel Johnson or their ilk with varying success. For the most part, I've avoided these academic spiritualists to focus on work that furthers our objective of building autonomous agents. Guy Deutscher's The Unfolding of Language is somewhat of a compromise, but his was the first I read and he helped to reshape my understanding of the origins and uses of language [34].
The subtitle of Deutscher's book "An Evolutionary Tour of Mankind's Greatest Invention", is intentionally misleading. Deutscher begins by lauding our invention of language only to subsequently deflate our collective ego by pointing out that no individual institution or governing body can be held responsible for human language — it evolved, and the way in which it evolved and the corresponding selective pressures that directed its evolution are the focus of Deutscher's book. Deacon makes the case that humans and language coevolved and that language is an emergent phenomena dependent on the complexity of the life forms that employ language and the environment in which their lives play out. There are consequences of Deacon's theory that become apparent in reading these three evolutionary accounts, and that make reading my summary of Deacon's Incomplete Nature worth the effort. Here is Deutscher stroking our high opinion of ourselves, only to reveal that whatever role we might have had in the evolution of language it is more along the lines of a worker ant than a Boswell, Diderot or Hume:
Of all mankind's manifold creations, language must take pride of place. Other inventions — the wheel, agriculture, sliced bread — may have transformed our material existence, but the advent of language is what made us human compared to language, all other inventions pale in significance since everything we have ever achieved depends on language and originates from it. Without language we could never have embarked on our ascent to unparalleled power over all other animals, and even over nature itself. [ ... ] Even so, there is just one flaw in all these hymns of praise, for the homage to language's unique accomplishments conceals a simple yet critical incongruity. Language is mankind's greatest invention — except, of course, that it was never invented. Excerpt from Page 1 in The Unfolding of Language by Deutscher [34].
To explain the evolution of linguistic norms, Duetcher begins by describing the different forces acting on the initial selection, subsequent adoption, creative amendment and inevitable corruption and wholesale rejection of linguistic variations. He begins with destruction:
First to come under the magnifying glass will be the forces of destruction, for the devastation they wreak is perhaps the most conspicuous aspects of language's volatility. And strangely enough, it will also emerge that these forces of destruction are instrumental in understanding linguistic creation and regeneration. Above all they will be indispensable for solving a key question: the origin of the "raw materials" for the structure of language. [ . . . ] One thing is certain: in language, as in anything else, nothing comes from nothing. Only very rarely are words "invented" out of the blue (the English word "blurb" is reputedly one of the exceptions). Certainly, grammatical elements were not devised at a prehistoric assembly one summer afternoon, nor did they rise from the brew of some alchemist's cauldron. So they must've developed out of something that was already at hand. But what?The answer may come as rather a surprise. The ultimate source of grammatical elements is nothing other than the most mundane everyday words, unassuming nouns and verbs like "head" or "go". Somehow, over the course of time, plain words like these can undergo drastic surgery, and turned into quite different beings altogether: case endings, prepositions, tense markers and the like. To discover how these metamorphoses take place, we'll have to dig beneath the surface of language and expose some of its familiar aspects in an unfamiliar light. But for the moment just to give a flavor of the sort of transformations we'll encounter, think of the verb "go" — surely one of the plainest and most unpretentious of words. In phrases such as "go away!" or "she's going to Basingstoke", "go" simply denotes movement from one place to another. But now take a look at these sentences:
Is the rain ever going to stop?
She's going to think about it.Here, "go" has little to do with movement of any kind: the rain is not literally going to anywhere to stop, in fact it has no plans to go anywhere at all, nor is anyone really "going" anywhere to think. The phrase "going to" merely indicates that the event "be going to" can be replaced with "will" in these examples without changing the basic meaning in any way:
Will the rain ever stop?
She will think about it.So what exactly is going on here? "Go" started out in life as an entirely ordinary verb, with the straightforward meaning of movement. But somehow, the phrase "going to" has acquired a completely different function, and has come to be used as a grammatical element, a marker of the future tense. In this role, the phrase can even be shortened to "gonna", at least in informal spoken language:
Is the rain ever gonna stop?
She's gonna think about it.
but if you try the same contraction when "go" is still used in the original meaning of movement, you're going to be disappointed. No matter how colloquial the style or how jazzy the setting, you simply cannot say "I'm gonna Basingstoke". So "going to" seems to have developed a kind of schizophrenic existence, since on the one hand it is still used in its original "normal" sense ("she's going to Basingstoke"), but on the other it has acquired an alter ego, one that has been transformed into an element of grammar. It has a different function, a different meaning, and has even acquired the possibility of a different pronunciation. Excerpt from Pages 10-11 in The Unfolding of Language by Deutscher [34].
Some of the earliest work in AI on natural language processing (NLP) both absorbed from and contributed to the fields of cognitive science and computational linguistics. Unfortunately, many AI researchers attacked the dual problems of production and understanding as if they only had write down the rules of grammar (syntax), the definitions of words (semantics), and encode any relevant knowledge as symbolic structures using propositional or first-order logic (logical forms), frame- or script-based representations (slot-filler notations) and relational graphs (hierarchies and taxonomies) and we'd be done with it, just like some thought that computer vision was a summer's work for an undergraduate MIT student93 .
For example, Conceptual Dependency Theory [111] developed by Roger Schank built on the work of Sydney Lamb who developed his Relational Network Theory of Language as a significant challenge to Chomsky's transformational grammar. Script Theory is a psychological theory developed by Silvan Tomkins that posits human behavior largely falls into patterns called "scripts" because they function analogously to the way a written script does, by providing a program for action. Schank and Abelson [112] extended Tomkins' scripts in developing AI applications. Marvin Minsky's Frames predate scripts and are closely related in terms of representational power.
There was some effort to create internal representations that serve to ground linguistic forms and functionally group concepts. It was thought that by doing so one could exploit generalizations to simplify understanding and exhibit the sort of varied production we observe in human speech. Here, for example, is a partial taxonomy of primitive actions provided in conceptual dependency theory [111]:
-
State Changes physical and abstract transfers:
PTRANS: to change the location of a physical object.
ATRANS: to change an object's abstract relationship.
SPEAK: to produce a sound intended for communication.
ATTEND: to direct a sense organ or focus on stimulus.
MTRANS: to transfer information mentally.
MBUILD: to create or combine thoughts.
Mental and Cognitive actions and activities:
Instruments for other actions and activities:
Unfortunately, these approaches — now collectively referred to as "good old-fashioned AI" (GOFAI) — proved to be brittle and not amenable to the machine learning technology of the time. Douglas Hofstadter pointed out the inflexible nature of such representations and characterized a possible solution in terms of what he referred to as fluid concepts and creative analogies [61, 60, 59]. The connectionists focused on a biologically-inspired approach to exploiting distributed processing, context sensitivity and continuous (smoothly varying and differentiable) adaptation / responsiveness to environmental change, but were stymied by the seeming intractability of learning artificial neural networks due, in part, to the so-called vanishing gradient problem.
Modern ANN technology has demonstrated multiple viable approaches to learning complex networks and shown how ANN representations can effectively solve interesting computer vision and natural language processing problems. So why don't we all have personal assistants capable of continuous conversation across a wide range of topics and working collaboratively with us to solve practical problems? There are a number of reasons typically cited, ranging from the lack of physical grounding or semantics of any sort — McDermott's "no notation without denotation" was a challenge [79] to the AI community to adopt Tarskian semantics — to the difficulty of common sense reasoning. The attempt to encode a "naïve physics" model of the world tailored to everyday speech was part of the — largely failed — effort to formalize the common knowledge of human beings.
On Page 133 of Deutscher's book [34], he quotes the Encyclopedia Britannica article on the concept of 'space-time', "In physical science, 'space-time' is a single concept that recognizes the union of space and time, posited by Albert Einstein in the theories of relativity (1905, 1915). Common intuition previously supposed no connection between space and time." To this, Deutscher responds "everyday language proves that 'common intuition' has in fact recognized this link for many thousands of years (even if not exactly an Einstein's sense)." There is now evidence that hippocampal structures in both rodents and humans support a form of sequence memory that combines both temporal and spatial information94 . Deutscher goes on to provide many examples to support his observation, and includes this interesting table:
|
Later he mentions that "like most of the metaphors already encountered, the images here are ultimately grounded in experience — think of a sentence like 'the travelers got typhoid from the contaminated water'. The physical origin of the disease is also its cause: the disease started because of the water, but it also came — physically — from it. But in generalizing the metaphor, we have unshackled the image from that basis in experience, and can now talk freely about one thing coming 'from' another, 'out of' another, or happening 'through' another, to express abstract chains of cause and event."
Deutscher makes many interesting observations about the everyday use of language. I'll mention two additional examples before turning to summarize what I've learned from reading the book. On Page 31, he notes that language with only words, with no structure — hierarchy, nesting, connectives, truth functionals, recursion — to prop them up would be a poor instrument of communication, and, on Page 45, he observes the obvious that "the names we use for things bear no inherent relationship to the things themselves. The names are entirely arbitrary, and this is why [the German word for spoon] 'löffel' or [the French word for spoon] 'cuillère' is just as good a designation for a [drawing or photograph of a spoon] as [the English word] 'spoon'" — a comment that apparently needs repeating as we read contemporary commentary on the role of language in everyday life.
We started this inquiry trying to understand human language both as a technology for communicating ideas and as a framework for exploring, incubating, and creating new ideas. Now, more than six books and several dozen journal articles later, I have pretty much come full circle. Yes, brains compute but they are also memory, indeed they integrate multiple memory systems each of which has its own neural mechanisms and natural use cases. Language production and understanding are built upon and constrained by the brain's various memory systems; however, in developing advanced AI systems that borrow from what we've learned about human brains, we need not be slavishly bound by such constraints.
Alternatives to the notion of a universal grammar have received more attention lately as the number of linguists under the thrall of Chomsky's theory has waned in recent years. While we can thank Chomsky for freeing language from the stifling influence of behaviorism, present day computational and cognitive linguists offer compelling alternative explanations for the seemingly infinite variety of human language suggesting that simple phrasal templates can account for a good deal of everyday language [24]. Moreover a full account of human linguistic competence based on natural selection follows from an understanding of general learning and processing biases deriving from the structure of natural thought processes [21, 23, 22].
A grammar is just one way of describing the syntactic structure of a language — a prescribed, collectively acquired set of constraints, but human language users can communicate using what most linguists would consider a very simple grammar. We have suggested that we begin with the most basic methods for signaling and referring. We should look carefully at the work in developmental psychology relating to how children acquire such basic communicative tools, considering them as an essential foundation for more sophisticated language use. Given what we know about how various memory systems mature in the developing brain, it is no surprise that sophisticated language skills develop later.
Historically, psychologists and neuroscientists group different memory systems as being either short-term or long-term with short-term memory95 handled by neural mechanisms involving the basal ganglia and prefrontal cortex requiring some form of active maintenance, whereas long-term memory96 is handled by the hippocampal-entorhinal complex and doesn't require active maintenance. This model works when we consider simple tasks like remembering a sequence of words and repeating at some later time. It doesn't appear to work well when subjects are interrupted in the midst of performing a task.
That some human subjects are able to handle so-called distractor tasks suggests that some subjects have more short-term storage capacity or are more adept at actively maintaining what short-term memory they have, or perhaps there is some yet-to-be discovered form of intermediate-duration storage that plays a similar role to that of a buffer, stack or local cache in modern computer architectures. The term working memory is sometimes used synonymously with short-term memory but some accounts ascribe working memory a larger role in decision making and problem solving97.
In my experience, if you're interested in deeply understanding anything reasonably complex, it helps to read or listen to several different authors and speakers, for reasons of completeness, multiple perspectives and different ways of thinking — preferably those who are both clear and reasonably succinct. Neil Burgess is particularly articulate and economical in his exposition of a number of topics relating to our discussion of human memory, including both short-term memory, long-term (episodic) memory and spatial navigation — see also his Neuron article on spatial and episodic memory with Eleanor Maguire and John O'Keefe [14].
Michael Corballis [24] follows William James in treating stories and storytelling as a mode of "narrative, descriptive, contemplative" thinking, and links it to our "capacity to travel mentally in time and space and into the minds of others, along with a dose of imaginative construction." Regarding the role of episodic memory, he quotes Catherine Nelson [86] in writing about storied thoughts, "narrative models and early influences in early childhood help to transform the episodic memory system into a long-lasting autobiographical memory for one's own life, and thus a self history, which to a large extent underlies our concept of self" and notes the natural tendency of children to engage in playful fantasy, often blending fact and fantasy and delighting in the telling of frightening events and disasters. Corballis also mentions the natural tendency of children to act out the scripts of life, such as feeding a baby, doing a medical checkup and cooking a meal. The repeating of old stories and reliving old memories, trotting them out when appropriate to teach a lesson as in the case of telling epic stories.
In the third and final part of his book, Corballis explains how language evolved as a communication system for sharing thoughts and experiences. Some of what he has to say repeats what we have heard from other authors, including how expressive language originated in bodily gestures, as opposed to vocally articulated calls and warnings, and how vocalizing gradually evolved, eventually coming to dominate as the mode of choice in communicating intent. he weaves in the idea of motor neurons providing detail about the cell types and their locus in human brains he writes
It is now clear that our brains house a mirror system. A meta-analysis of 125 studies using functional magnetic resonance imaging revealed 14 clusters of neurons with mirror properties. These were located in areas homologous to those identified in the monkey brain, including the inferior parietal lobule, inferior frontal gyrus, the ventral prefrontal cortex, but also included regions in the primary visual cortex, the cerebellum, and the limbic system. In another remarkable study a group of investigators recorded activity directly in over a thousand single neurons in the brains of patients about to undergo surgery. A significant portion of these neurons responded to both observation and execution of movements of the hand and face. The areas included area F5, along with other areas associated with language and gesture in the frontal and temporal lobes. And not surprisingly, the human mirror system does indeed overlap with Broca's and Wernicke's area. Excerpt from Page 130 in The Truth About Language by Corballis [24]
Corballis mentions Hickok and Poeppel [56] on their dual pathways theory of speech perception. His summary should provide motivation to read his full account or read Hickok and Poeppel if you want more detail:
Hickok and Poeppel have suggested what they call a "dual stream" theory of speech perception. One stream is lower in the brain: the so-called ventral stream, which progresses from the temporal lobe to the frontal lobe of the brain. This stream is responsible for the understanding of speech, and it is presumably this stream, or its homologue, that is responsible for the limited understanding of human speech and Kansi or in dogs like Rico and Chaser — and perhaps even your pet cat, not to mention inarticulate teenagers. The other stream is higher: the so-called dorsal stream, which flows from the parietal lobe and is responsible for the actual production of articulate speech. It is this component that is lacking in dogs and apes.The dorsal stream is part of the mirror system and may indeed play a role in perceiving as well as in producing action, as implied by the motor theory of speech perception. In an extensive critique of mirror-neuron theory, Greg Haycock suggests that the mirror system is not so much a device for tuning into speech sounds as a "feed forward" mechanism for calibrating the production of speech sounds. We shape our speech in terms of how we hear them — this, perhaps is why babies babble before they learn to speak. They are calibrating. The ability to speak may well modify the way we perceive speech, but, as the examples of dogs and apes show, perception of speech can occur without any influence of speech production. Hickok gives the analogy of observing a person playing the saxophone. A non-saxophone player may well have adequate perception of the player's performance, but a fellow saxophonist is likely to have an enriched perception and understanding by relating her perception to her own experience. Excerpt from Pages 151-152 in The Truth About Language by Corballis [24]
In the chapter entitled "How Language is Structured", mentions John O'Keefe's observations that "most prepositions in English, such as, about, across, against, among, along, around, between, from, in, through, and to, apply to both space and time and apply even to logical expression that are symbolic rather than spatial, as in "A follows from B" or the "argument against A is B. [...] O'Keefe also suggest that the hippocampus and adjacent structures gained an asymmetry [noting that] damage to the right mesial temporal lobe (which includes the hippocampus) results in amnesia for episodes coded in visuo-spatial terms while left-sided damage results in amnesia for episodes coded verbally98.
I was particularly interested in Corballis's discussion — Pages 184-187 — of how manufacture and the use of tools may have influenced the structure of language. He notes a grammar-like feature of toolmaking in the form of its "hierarchical nature, with subgoals that must be met within overarching goals. For example, in the removal of stone flakes, various 'subroutines' such as edging, thinning, and shaping need to be carried out before a flake is removed. One consequence of this is a separation in time between related operations — a subroutine must be completed before the toolmaker can return to the original goal. Likewise in language, one must retain information from the beginning of a sentence while a subordinate clause is processed before the rest of the sentence completes the meaning."
Assuming — as we have here — that you are a self-replicating, recurrent process, a thread of conscious awareness that continuously reimagines itself through its interaction with the environment and its internal mutable record of the past mediated by scores of unconscious threads of computation governed in part by the complex interplay of resident microbial and viral influences, ambient gases and airborne particulate matter, sustaining nutrients, neuromodulatory hormones and neurotransmitters largely under the control of primitive instincts that have persisted pretty much unchanged for millions of years [...] If you can read and understand the last sentence does that serve as evidence that you are human ... or that you are a Turing machine? [Note that "both" is also a legitimate answer.]
It is interesting to note that we are suggesting here that human language could be as simple as template matching and table lookup. The encoder-decoder model that we encountered in Figure 5 can used to generate often quite plausible responses when trained on utterance pairs extracted from conversation or call-center customer-operator sessions. Of course, to get it right often enough that customers don't just immediately hang up the phone, it's necessary to adapt the previously recorded response to suit the current circumstances. It's possible that much of what we say is generated by recalling something we or someone else said, modifying it superficially and producing it as if generated de novo. Perhaps the most eloquent and erudite among us are just better at disguising what would otherwise be considered as plagiarism or, more charitably, imitation.
From this perspective, communication and problem solving are all about bringing context to bear. What to say in a given situation and how to interpret what someone else is saying. What is relevant to think about in solving a problem and what can be discarded so as not to clutter the mind. The context sensitivity of connectionist models and the fluid properties of continuous vector representations are the friend of recall and the enemy of precision. For most children, their initial exposure to language and early development of a facility for its day-to-day application is full of opportunities to learn. Our immediate goal is to learn what's required to design, write and debug programs and not to challenge the likes of William Safire. Learning how to attend and refer to relevant information, following simple instructions such as evaluating a code fragment, asking for help ... these are the sort of activities the assistant needs to master in order to become useful.
Nick Chater [16] has written an interesting and provocative book hypothesizing that human cognition is "flat" in the sense that, apart from what is apparent in our conscious thoughts, there is very little else going on (unconsciously) in the background except for the sort of sensory processing that occurs in the visual and auditory areas of the cortex. My short summary of his book would be something like: human cognition consists primarily of our conscious thoughts substantially enhanced by imaginative (unconscious) recall of related memories stimulated by a combination of our recently activated thoughts and our cu-rent perceptions which are influenced by our emotional and cognitive state; all the rest of our thoughts are the result of unconscious, highly-parallel processing that are similar to what's going on in the visual cortex. You can read more of my thoughts on Chater's book in this footnote. Chater, Morten Christiansen and their various co-conspirators have also written a good deal about the origins of human language and the biological plausibility of our having an innate language facility such as Chomsky's universal grammar [21, 19, 17].
Communicating Code
The brain didn't evolve to accommodate language, rather, language evolved to accommodate the brain [17]. Biological and cognitive constraints determine what types of linguistic structure are learned, processed and transmitted from person to person and generation to generation. Language acquisition has comparatively little to do with linguistics and is probably best viewed as a form of skill acquisition. Indeed, we are constantly processing streams of sensory information into successively more abstract representations while simultaneously learning to recode the compressed information into hierarchies of skills that serve our diverse purposes [18, 19].
Contrary to what some textbook authors might think, students learn to code by writing programs, a process that can be considerably accelerated by timely communication with peers and invested collaborators. In the case of unequal skill levels, communication tends to be on the terms of the more capable interlocutor, and the onus of understanding on the less capable partner in the collaboration. To sustain the collaboration, we need to bootstrap the apprentice to achieve a reasonble threshold level of competence in both language and in working with computers so as to compensate for expert programmer's investment in effort. From a value-proposition perspective, the apprentice has to provide net positive benefit to the programmer from day one.
It is important to keep in mind that any program specification whether in the form of input/output pairs or natural language descriptions when communicated between individuals of differing expertise is just the beginning of a conversation. Experts are often careless in specifying computations and assume too much of the student. Students, on the other hand, can surprise experts with their logical thinking while frustrate and disappoint with their difficulty in handling ambiguity and analogy, particularly of the esoteric sort familiar to professional programmers. Input from an expert will typically consist of a stream of facts, suggestions, heuristics, shortcuts, etc., peppered with clarifications, interruptions and other miscellany.
We propose a hybrid system for achieving competence in communicating programming knowledge and collaboratively generating software by creating a non-differentiable conventional dialogue management system that works in tandem with a differentiable neural-network dialogue system (NDS) that will become more competent as it gains experience coding and collaborating with its expert partner. The deployment of these two language systems will be controlled on a sentence-by-sentence basis by a meta-reinforcement learning (MRL) system that will depend less and less on the more conventional system but likely never entirely eclipse its utility. The MRL system subsumes the role of a beam search or softmax layer in an encoder-decoder dialogue model.
The conventional system will be built as a hierarchical planner99 following in the footsteps of the CMU Ravenclaw Dialogue System [11] and will come equipped with a relatively sophisticated suite of hierarchical dialogue plans for dealing with communication problems arising due to ambiguity and misunderstanding. While clumsy compared to how humans handle ambiguity and misunderstanding, these dialogue plans are designed to resolve the ambiguity and mitigate the consequences of misunderstanding quickly and get the conversation back on track by attempting various repairs involving requests for definition, clarification, repetition and restatement in as inconspicuous manner as possible [10].
The conventional dialogue system will also include a collection of hierarchical plans for interpreting requests made by the expert programmer to alter programs in the shared editor space, execute programs on specified inputs and perform analyses on the output generated by the program, debugger and other tools provided in the integrated development environment (IDE) accessible through a set of commands implemented as either primitive tasks in the non-differentiable hierarchical planner or through a differentiable neural computer (DNC) interface using the NDS system that will ultimately replace most of the functions of the hierarchical-planner-based dialogue management system.
This dual mode dialogue system and its MRL controller allows the apprentice to practice on its own and rewards it for learning to emulate the less-flexible hierarchical-planner implementation. Indeed there is quite a bit that we can do to preload the apprentice’s basic language competence and facility using the instrumented IDE and related compiler chain. A parallel dialogue system implemented using the same hierarchical planner can be designed to carry out the programmer’s side of the conversation so as to train the NDS system and the meta-reinforcement learning system that controls its deployment utterance by utterance. We can also train domain-specific language models using n-gram corpora gleaned from discussions between pair programmers engaged in writing code for projects requiring the same programming language and working on similar programming tasks.
Cognitive and systems neuroscience provide a wide range of insights into how to design better algorithms and better artificial neural network architectures. From our study of the fly olfactory system we have learned new algorithms for locality sensitive hashing, one of the most important algorithms used for scalable nearest-neighbor search. The mammalian visual system is the most well studied area of the brain. Early on we discovered that the architecture of the visual system involved two separate pathways referred to as the dorsal and the ventral pathways and roughly characterized as being responsible for the "where" and "what" dimensions of visual stimuli.
Subsequently it was argued that other sensory modalities employed dual pathways and that the production and understanding of language were organized as such with Broca's and Wernicke's areas playing key roles in this architecture. The engineering insights we have gained studying the brain are cashed out in the technical language of different disciplines. For example, the dual loop language model as it's called is often presented as a block diagram consisting of conceptually separate neural networks. The Hodgkin-Huxley model of action potential propagation in the giant squid axon was described both as a system of differential equations and as an electrical circuit diagram.
This is not the place for a lecture on dialogue management, but I'll make just a few comments about how we might finesse the problem either by brute force approaches or by resorting to a highly structured subset of natural language sufficient for most of the communication that goes on between two programmers focused intently in working on a specific problem.
The CMU RavenClaw Dialogue Management Architecture recast dialogue management as hierarchical task-based planning, demonstrating how error recovery, new topic introduction, recursive structure, and other characteristics of conversational dialogue could be handled within this framework. We've experimented with this approach and it might be a good fit for a prototype version of the programmer's apprentice. A more ambitious approach might leverage the idea of value iteration networks to create a dialogue management system trained on real dialog. A hybrid alternative would be to combine the two approaches.
In 2013 we created a dialogue dataset from the logs of chat sessions between software engineers and technical support staff. We borrowed the idea that dialogue management as a specialized form of language translation in which both speakers use the same basic language but employ different word choices, and created a sequence-to-sequence encoder-decoder translation model. The dataset was relative small compared with most of our language translation datasets, but the performance was better than we had any right to expect. More sophisticated hierarchical architectures using various attentional mechanisms would no doubt outperform our earlier models.
Contextual Integration
Context is everything in language and problem solving. When we converse with someone or read a book we keep in mind what was said or written previously. When we attempt to understand what was said in a conversation or formulate what to say next we draw upon our short-term memories of earlier mentioned people and events, but we also draw upon our long-term episodic memories involving the people, places and events related to those explicitly mentioned in the conversation. In solving complex design problems, it is often necessary to keep in mind a large number of specific facts about the different components that go into the design as well as general knowledge pertaining to how those components might be adapted and assembled to produce the final product.
Much of a programmer’s procedural knowledge about how to write code is baked into various cognitive subroutines that can be executed with minimal thinking. For example, writing a simple FOR loop in Python to iterate through a list is effortless for an experienced Python programmer, but may require careful thought for an analogous code block in a less familiar programming language like C++. In thinking about how the apprentice’s knowledge of programming is organized in memory, routine tasks would likely be baked into value functions trained by reinforcement learning. When faced with a new challenge involving unfamiliar concepts or seldom used syntax, we often draw upon less structured knowledge stored in episodic memory. The apprentice uses this same strategy.
The neural network architecture for managing dialogue and writing code involves encoder-decoder pairs comprised of gated recurrent networks that are augmented with attention networks. We’ll focus on dialogue to illustrate how context is handled in the process of ingesting (encoding) fragments of an ongoing conversation and generating (decoding) appropriate responses, but the basic architecture is similar for ingesting fragments of code and generating modified fragments that more closely match a specification. The basic architecture employs three attention networks, each of which is associated with a separate encoder network specialized to handle a different type of context. The outputs of the three attention networks are combined and then fed to a single decoder.
The (user response) encoder ingests the most recent utterance produced by the programmer and corresponds to the encoder associated with the encoder-decoder architectures used in machine translation and dialogue management. The (dialogue context) encoder ingests the N words prior to the last utterance. The (episodic memory) encoder ingests older dialogue selected from episodic memory. The attentional machinery responsible for the selection and active maintenance of relevant circuits in the global workspace (GWS) will likely notice and attend to every utterance produced by the programmer. Attentional focus and active maintenance of such circuits in the GWS will result in the corresponding thought vector added to NTM the partition responsible for short-term memory.
The controller for the NTM partition responsible for short-term (active) memory then generates keys from the newly added thought vectors and transmits these keys to the controller of the NTM partition responsible for long-term (episodic) memory. The episodic memory controller uses these keys to select episodic memories relevant to the current discourse, combining the selected memories into a fixed-length composite thought vector that serves as input for the corresponding encoder. Figure 20 depicts the basic architecture showing only two of the three encoders and their associated attention networks, illustrating how the outputs of the attention networks are combined prior to being used by the decoder to generate the next word or words in the assistant’s next utterance.
| |
| Figure 20: In the programmer's assistant, the dialogue management and program-transformation systems are implemented using encoder-decoder sequence-to-sequence networks with attention. We adapt the pointer-generator network model developed by See et al [113] to combine and bring to bear contextual information from multiple sources including short- and long-term memory systems implemented as Neural Turing Machines as summarized in Figures 52 and 53. This graphic illustrates two out of the three contextual sources of information employed by the apprentice. Each source is encoded separately, the relevance of its constituent elements represented as a probability distribution and resulting distributions combined to guide the decoder in generating output. | |
|
|
Memory Consolidation
One step of the decoder could add zero, one, or more words, i.e., a phrase, to the current utterance under construction. Memories — both short- and long-term — are in the form of thought vectors or word sequences that could be used to reconstruct the original thought vectors for embedding or constructing composites by adding context or conditioning to emphasize relevant dimensions. The dialogue manager — a Q-function network trained by reinforcement learning — can also choose not to respond at all or could respond at some length perhaps incorporating references to code, explanations for design choices and demonstrations showing the results of executing code in the IDE.
To control generation, we adapt the pointer-generator network framework developed by See et al for document summarization [113]. In the standard sequence-to-sequence machine-translation model a weighted average of encoder states becomes the decoder state and attention is just the distribution of weights. In See et al attention is simpler: instead of weighting input elements, it points at them probabilistically. It isn't necessary to use all the pointers; such networks can mark excerpts by pointing to their start and end constituents. We apply their approach here to digest and integrate contextual information originating from multiple sources.
In humans, memory formation and consolidation involves several systems, multiple stages and can span hours, weeks or months depending on the stage and associated neural circuitry100. Our primary interest relates to the earliest stages of memory formation and role of the hippocampus and entorhinal region of the frontal cortex along with several ancillary subcortical circuits including the basal ganglia (BG). Influenced by the work of O'Reilly and Frank [90], we focus on the function of the dentate gyrus (DG) in the hippocampal formation and encode thought vectors using a sparse, invertible mapping thereby providing a high degree of pattern separation in encoding new information while avoiding interference with existing memories.
We finesse the details of what gets stored and when by simply storing everything. We could store the sparse representation provided by the DG, but prefer to use this probe as the key in a key-value pair in the NTM partition dedicated to episodic memory and store the raw data as the value. This means we have to reconstruct the original encoding produced when initially ingesting the text of an utterance. This is preferable for two reasons: (i) we need the words — or tokens of an abstract syntax tree in the case of ingesting code fragments — in order for the decoder to generate the apprentice's response, and (ii) the embeddings of the symbolic entities that constitute their meaning are likely to drift during ongoing training.
Hierarchical Memories
Language, programs and plans are all usefully thought of as having hierarchical, recursive structure. It also makes sense to think of brains as being organized as such, and the human brain employs hierarchical models to make sense of the world in which it evolved. Sensory information enters central nervous system in separate streams for each of the different senses, vision, hearing, taste, smell, etc., but is quickly processed to extract useful features and combinef to construct abstract concepts that allow us to recognize similarities and exploit differences.
To the untutored mind, the world is essentially flat. We impose hierarchical structure to make understanding it more tractable. We ingest sequences of observations as input and execute sequences of actions as output. What goes on between is complicated. We start by consulting a map of the human brain and relating different anatomical regions with the functional roles we believe they play in cognition. There is a great deal we still don't know about the brain and much of what is written here is provisional. That said, for the most part we stick to what is generally agreed upon, and will alert you if we deviate substantially from current consensus. Enamored as we are with our highly evolved cortex, much of the discussion will focus on this part of the brain. However, the cortex is built on top of a highly conserved foundation of subcortical regions without which we would be reduced to gibbering idiots.
Humans tend to organize information in hierarchies that are based on different methods of cataloguing data. Sometimes they correspond to class-subclass hierarchies as are used in taxonomic classifications, e.g., species, genus, family. Class hierarchies are different from what are commonly referred to as compositional hierarchies, with features at one level in the hierarchy constructed from the features in the subordinate level as in the case of part-whole hierarchies, e.g., the carburetor is part of the engine and the engine is part of the car, or feature hierarchies in object recognition, e.g., lines, vertices, edges and surfaces.
The human brain seems to naturally use all of these strategies and more, sometimes in combination, but hardly ever in the clean tidy way that scientists create taxonomies and engineers catalog engineered artifacts. In the visual system, we see examples of what appear to be compositional models in which small features that represent little fragments of lines are composed to create longer lines which in turn become the boundaries of objects. There are more than a dozen topographically mapped representations in the primate visual system and while they roughly constitute an hierarchy of features, that may have more to do with what we expect to see.
Machine learning researchers have come to realize that it's a bad idea to impose what you might think are the right features for representing something. It is generally better to let the data speak for itself in generating appropriate features for representation. One drawback of this is that the representations the learning system builds are often said to be uninterpretable which can be a problem if, for example, you are learning to identify tumors in tissue samples for performing biopsies and want a human expert to pass judgment on how well the system is working. Fortunately, it is often possible to learn generative models that allow researchers to visualize learned features.
Some search engines still depend on hierarchical models in which documents are composed of sections, that are composed of paragraphs that are composed of sentences, phrases, words and letters. Nowadays machine learning experts are more likely learn generative models of text and not impose biases that are more often than not misguided [1, 141]. Your brain routinely constructs complex representations of events that encode a wide range of relevant information — relevant, that is, to your particular interests. Seeing an old photo might cause you to recall the person who took the photo, the location where it was taken, what you had for dinner that night, etc.
Bootstrapped Language
In this section, we consider how we might design an end-to-end training protocol for bootstrapping a variant of the programmer's apprentice application. We begin with the analogous stages in early child development. Each of the following four stages is briefly introduced with additional technical details provided in the accompanying footnotes:
Basic cognitive bootstrapping and linguistic grounding101:
modeling language: statistical \({n}\)-gram language model trained on programming corpus;
hierarchical planning: automated tutor generates lessons using curriculum training;
Simple interactive behavior for signaling and editing103:
following instruction: learning to carry out simple plans one instruction at a time;
explaining behavior: providing short explanations of behavior, acknowledging failure;
Mixed dialogue interleaving instruction and mirroring104:
classifying intention: learning to categorize tasks and summarize intentions to act;
confirming comprehension: conveying practical understanding of specific instructions;
Composite behaviors corresponding to simple repairs105:
executing complex plans: generating and executing multi-step plans with contingencies;
recovering from failure: backtracking, recovering, retracting steps on failed branches;
Chimps are apparently better than humans in tasks that require rapidly acquiring the details of a visual scene. In the wild, their near photographic memory allows them to quickly ascertain possible threats at a glance. In an experimental setting, they exhibit better recall than humans in trials where they are shown, say, an image showing single digits scattered across a background of contrasting color for a few milliseconds, and then tested on whether than can point to where each digit was in numerical order. In this sense, chimps may be likened to humans with autism who display weak central coherence, i.e., an eye for detail, but without the corresponding big-picture [77, 76]. One hypothesis is that humans are slower due, in part, to their more developed linguistic capacity that causes them to attend to the meaning of the individual stimuli as well as the relationships between them et al [107]106.
2.15 The History of Ideas
Hebb, Lashley, Pribram
Donald O. Hebb (1904-1985) was an extraordinary scientist and educator. He is probably best known for his unforgettable aphorism "neurons that fire together wire together", but there is so much more he contributed to psychology, neuroscience and our understanding of the human brain. His 1949 "The Organization of Behavior" had a profound impact on the direction of psychology and the creation of neuroscience as a scientific discipline [54]. I've included a short biography highlighting his contributions to science and his lifelong passion for teaching and scholarship while on the faculty of McGill University. I highly recommend this wonderfully scripted, narrated and graphically animated video produced at the University of British Columbia illustrating Hebb's postulates as applied to learning in the hippocampus.
The history of neuroscience and the study of human brain makes fascinating reading, both for the history of ideas and for insights into the fascinating people who were drawn to this field and persevered despite the technical and intellectual challenges of trying to understand one of the most complicated systems we know of. The Society for Neuroscience has created an archive of interviews with some of the most influential scientists who have contributed to our understanding of the many different areas of scientific inquiry relating to the study of neuroscience. Transcripts of the interviews are available from SfN for download as PDF files and there are video recordings for many of the interviews available from the SfN website or on the SfN YouTube channel. Hebb didn't live long enough to be included in the SfN archives, but the Canadian Association for Neuroscience has a short biography covering his major contributions.
William Maxwell Cowan (1931-2002) was a South African neuroscientist known for his work on developmental plasticity and neural connectivity. He is credited with helping to contribute to the growth of modern neuroanatomy through his use of novel anterograde tracing techniques which fundamentally transformed the field in the 1970s. His video interview for Society for Neuroscience History of Neuroscience archive is fascinating both for Cowan's choice of animal models and neural circuits to work on, e.g., connections involving the striatum, thalamus and other basal ganglia, the development of connections in the dentate gyrus and hippocampus, and the tools that he either employed or invented in his study of the retina and visual pathways.
Relative to our discussion of episodic memory, I highly recommend that you watch the interview with Mortimer Mishkin, former senior investigator at NIH and current chief of the section on cognitive neuroscience in the laboratory of neuropsychology at NIMH. The interview took place April 5-6, 2006. This video is part of the Society for Neuroscience's autobiography series, "The History of Neuroscience in Autobiography," detailing the lives and discoveries of eminent senior neuroscientists. Mortimer studied with two pioneers in neuroscience Donald Hebb and Karl Pribram whose ideas continue to influence the field to this day. Mortimer and his colleagues challenged the prevailing theory concerning organization of the brain due to Karl Lashley and provided evidence supporting a new understanding of how we process and remember visual information. Mishkin speaks in detail about the experiments he conducted, what they thought they knew at the time and what they learned as a result of their studies.
Karl Pribram worked with Karl Lashley at the Yerkes National Primate Research Center which is part of Emery University in Atlanta, Georgia. Pribram challenged Lashley's theory that any particular memory — or engram — did not exist in any specific part of the rat's brain, but that memory was widely distributed throughout the cortex. "In Lashley's experiments, rats were trained to run a maze. Tissue was removed from their cerebral cortices before re-introducing them to the maze, to see how their memory was affected. Increasing the amount of tissue removed degraded memory, but more remarkably, where the tissue was removed from made no difference". On the other hand, Pribram removed large areas of cortex and smaller areas that respected areal — possibly functional — boundaries formed by gyri and sulci, leading to multiple serious deficits in memory and cognitive function. In this interview commissioned by the American Association for Neurological Surgeons, Pribram describes his work at Yerkes and his realization that many functions that appeared to be carried out entirely within the cerebral cortex actually involved processes that descend into subcortical regions including the hippocampus and basal ganglia and even extending into the brain stem. Pribram comments on his epiphany around 00:21:00 minutes into the interview and mentions Mortimer Mishkin's contributions relating to the hippocampus and entorhinal cortex.
On the Hard Problems
I feel I should probably say something about consciousness, but believe the computational account provided in this chapter speaks for itself, and have read too much to think I could change any minds. However, there are a few voices I respect and so I will channel their enthusiasm by quoting excerpts from their writing and speaking. I strongly agree with Stanislas Dehaene's view of consciousness as expressed in this twenty minute video and summarized: "Stanislas Dehaene argues against the philosophical dualism of mind and brain and believes that consciousness is not a magical property but evolved for flexibility and adaptation." I agree with Daniel Dennett though I wish he didn't feel the need to address the concerns of every philosopher and scientist who ever expressed an opinion about consciousness. He has much to say and a good deal of it worth reading. I enjoyed Felipe de Brigard's compelling comments concerning David Chalmers' "hard problem of consciousness" at 01:03:00 into this discussion on NEURO.tv [70] produced by Dianna Xie and Jean François Garièpy. While researching Douglas Hofstadter's work on analogy, I ran across his book "I Am A Strange Loop" [62] in which he explores the idea of consciousness and the concept of "self". In comparing his account of consciousness with that of Dehaene, Graziano, Dennett and others we've discussed in these notes, I find Hofstadter's liberating in the way he avoids many of the earlier philosophical, psychological, biophysical and metaphysical conundrums that make this topic so confusing and fraught with controversy for the uninitiated. That said, I think some of you may find that this video retelling by Will Schoder entitled You Are A Strange Loop does Hofstadter's account one better and achieves its weight and clarity in a scant twenty minutes.
Emergent Phenomena
There are many disciplines that study the brain and for the most part they have different criteria for what it might mean to understand the brain. For example, there are neuroscientists who study the brain from the perspective of molecular biology. This could involve understanding the dynamics of how proteins, sugars, lipids and other types of molecules interact with one another to produce behavior at the molecular level e.g., how the proteins and lipids that make up neural cell membranes enable the selective passage of ions required to initiate and propagate neural signals along dendrites and axons. Some neuroscientists studied the genetic pathways that are ultimately responsible for most everything that happens within the brain. These disciplines tend to have a reductionist approach to doing science and are primarily interested in theories that explain how behavior arises at the most basic level.
Artificial and biological networks have in common the characteristic that it is difficult to map activity patterns at the level of individual neurons to the complex behaviors produced by the system as a whole. Explanations of how neural firing patterns give rise to observable behavior often tail off with an unsatisfying appeal to the idea of emergence in which the complex interactions between individual elements of a complex dynamical system give rise to surprisingly ordered behavior. The kinetic theory of gases allows us to predict the behavior of individual particles but is mathematically cumbersome if you want to understand how the curve of a wing provides lift for a bird in flight or predict the path of a hurricane. The tools of fluid dynamics provide a more tractable framework for studying aerodynamics and predicting weather. In the case of neuroscience, not only do we lack the models necessary to extrapolate from the activity of individual neurons to the composite behavior of ensembles of neurons whereby we solve simple word problems, we don't even have suitable technology for accurately measuring the related physical processes at multiple scales so as to provide the necessary data to construct and evaluate such models.
In contrast with cellular and molecular neuroscience, the cognitive neurosciences [44] are concerned with more complex behavior of the sort that give rise to the macroscale activities by which we interact with the physical world. Ultimately, they too would like explanations that connect observable behavior with the neural circuitry that gives rise to it, but the phenomena that they are concerned with is said to be an emergent property of the complex behavior of molecules. A single theory that extended from, say, the interaction of molecules to the production of speech acts is likely to be cumbersome and limited in its explanatory value, for example, in diagnosing behavioral problems in young children. Ultimately, what we need is a hierarchy of models each of which designed for a particular purpose so that the gap between any two layers of this hierarchy is small enough that it is possible for the corresponding models to bridge that gap in a manner that yields explanations suitable for some predictive or diagnostic purposes107.
The primary tools of cognitive neuroscience allow us to observe proxies for the gross behavior of such ensembles as in the case of using functional MRI to measure average blood oxygen levels within voxels on the order of a few millimeters on a side. Blood oxygen level is a lagging indicator for metabolic processes that are necessary in order for neurons to fire and for information to flow across the synaptic cleft from one neuron to another. The advantage of this technology is that it allows us to study the neural correlates of complex problem-solving behavior in human beings without surgery or other invasive methods of collecting data. Even if we could record from every neuron in the brain of an awake behaving human being without endangering the subject, it is not clear that we could make sense of the resulting tsunami of data — on the order of 100 billion neurons and well over 100 trillion synapses at millisecond temporal resolution, but there are certainly those of us who would like to try. Currently the best we can hope for is to record such data in a more tractable subject such as a fruit fly or juvenile zebrafish both of which have something on the order of 100,000 neurons, and even this will pose a considerable challenge to existing technologies.
Imagine you are walking in a forest in late Fall. The native birches and oaks have lost most of their foliage and it hasn't rained in weeks. A light breeze has been rustling the dry leaves, but now the wind is picking up and the few leaves left on the trees are taking flight, swirling through the forest like a flock of starlings. Up ahead is a clearing warmed by the sun. In the resulting thermal updraft, the leaves are swept up and disperse as if starlings are fleeing in disarray from a predatory hawk or falcon. How would you model this common but relatively complex behavior?
A physicist could choose from several theoretical frameworks depending upon his or her target level of explanation, e.g., quantum electrodynamics (QED), the kinetic molecular theory of gases, fluid dynamics (FD) or start by describing a computational finite-element model and then use one of the earlier frameworks to define the boundary equations as is done in weather and climate predictions. Each option has its own specific practical consequences, and a good scientist or engineer understands the limitations and advantages of the available modeling tools.
In the case of our walk in the woods, the behavior we observe arises out of interactions between familiar objects that are themselves complex physical systems that have their own dynamics and explanatory frameworks that may or may not be relevant if a detailed accounting does not substantially alter the predictions we might wish to make. It is reasonable expect that an explanation at the level of QED or even FD provides more detail than required for most purposes and that carrying out the necessary calculations or establishing the appropriate boundary conditions is prohibitive in any case.
Your body exhibits emergent properties that can be partially explained at the molecular level but are made clearer by appeal to their gross (motor) function. You are an emergent phenomenon. You learn and use language. You make predictions and construct plans. You have feelings and experience emotion. The society that you were born into has emergent properties that can't easily or succinctly be described at the molecular or cellular level. It is difficult if not impossible to adequately explain your behavior without taking into account the physical and social environment you inhabit.
Sir John Eccles who shared 1963 Nobel Prize in Physiology or Medicine for his work on the synapse with Andrew Huxley and Alan Lloyd Hodgkin believed that synaptic transmission was primarily electrical rather than chemical. He believed this so strongly that he discouraged those who challenged his theory. The fact is he was partially right. Models that strongly adhere to his bias have turned out to be extraordinarily useful in accounting for some of the neural activity we observe, but they have proved inadequate when it comes to explaining many brain disorders that arise from biochemical signaling108 .
The point is that explanations based on faulty or inadequate theories are inevitable and that, moreover, they often provide value in terms of adequately explaining phenomena. Theories that abstract from the details in order to account for emergent phenomena play an essential role in science. In either case, we have to remain reasonably skeptical. Today most biomedical students know that protein phosphorylation mediates a wide range of neural phenomena, and, in particular, gives rise to many debilitating brain disorders. It would be naïve to believe that there are no remaining significant deficits in our basic understanding of neurons109.
In this chapter, we have attempted to explain how interactions between neurons on a microscopic scale — that we are just beginning to understand — produce behavior on a macroscopic scale using the technology of artificial neural networks — that we understand insofar as we can build such systems, control every characteristic of their design and observe every nuance of their behavior. Artificial neural networks serve as a bridge across multiple scales by sacrificing some features in order to reduce complexity and gain insight into other features.
2.16 Key Ideas Summary
References
1 In linear algebra, an idempotent matrix is a matrix that, when multiplied by itself, yields itself. That is, the matrix \({\mathbf{M}}\) is idempotent if and only if \({\mathbf{M^{2} = M\,M = M}}\). For some time now, I've been corresponding with a group of like-minded physicians, scientists and engineers concerning the beneficial applications of artificial intelligence and the prospect of inverting the matrix, referring to the dystopian world of the eponymous matrix of science fiction movie fame.
If \({M}\) is a matrix and \({M^{-1}}\) is the inverse of \({M}\), then \({M^{-1}\,M = I}\) where \({I}\) is the identity matrix that maps any matrix \({M'}\) to itself, \({M'\,I = M'}\). The identity matrix is the mathematical equivalent of the injunction to "do no harm", a variant of which is ascribed to the Hippocratic Oath. Doing nothing is not equivalent to doing no harm, and so, in fact, the relevant portion of the Hippocratic Oath is generally translated as "first, do no harm", and thus we aspire to considerably more than simply maintaining the status quo.
2 There are hundreds of named neuronal cell types in the brain. The names have varying degrees of exactness and currency, ranging from the famously distinctive Purkinje cell to many lesser, poorly defined cells. Like genes, some cells appear under several names. Often, earlier nomenclatures have been abandoned as more precise ways of classifying cells developed [117, 75].
3 The neuron doctrine is the concept that the nervous system is made up of discrete individual cells, a discovery due to decisive neuro-anatomical work of Santiago Ramón y Cajal. The term neuron was itself coined by Waldeyer as a way of identifying the cells in question. The neuron doctrine, as it became known, served to position neurons as special cases under the broader cell theory evolved some decades earlier. (SOURCE)
4 The controversy surrounding estimates of the number of neurons and glia in the adult human brain is a textbook example of how false and misleading information about seemingly simple facts about the brain can originate, become enshrined in textbooks as facts and promulgated by otherwise well informed and well intentioned scientists for decades [131, 55, 3].
5 In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class.[1] It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector. (SOURCE)
6 A multilayer perceptron (MLP) is a class of feedforward artificial neural network that consists of, at least, three layers of nodes: an input layer, a hidden layer and an output layer. Except for the input nodes, each node is a neuron that uses a nonlinear activation function. MLP utilizes a supervised learning technique called backpropagation for training. It can distinguish data that is not linearly separable. (SOURCE)
7 A deep neural network (DNN) is an artificial neural network (ANN) with multiple layers between the input and output layers. (SOURCE)
8 The algorithm used to train a single layer perceptron is generally called the perceptron learning rule and is different from the method of backpropagation used to train multilayer perceptrons and deep neural networks. As far as we are concerned here, it is mainly of historical significance and to point out the limitations single-layer perceptrons when compared with multilayer perceptrons and deep neural networks. (SOURCE)
9 Backpropagation is a method used in artificial neural networks to calculate a gradient that is needed in the calculation of the weights to be used in the network. Backpropagation is shorthand for "the backward propagation of errors," since an error is computed at the output and distributed backwards throughout the network’s layers. It is commonly used to train deep neural networks. (SOURCE)
10 In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices, nodes, or points which are connected by edges, arcs, or lines. Graphs are one of the prime objects of study in discrete mathematics. (SOURCE)
11 In graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets \({U}\) and \({V}\) such that every edge connects a vertex in \({U}\) to one in \({V}\). The complete bipartite graph on \({m}\) and \({n}\) vertices, denoted by \({K_{n,m}}\) is the bipartite graph \({G=(U,V,E)}\), where \({U}\) and \({V}\) are disjoint sets of size \({m}\) and \({n}\), respectively, and \({E}\) connects every vertex in \({U}\) with all vertices in \({V}\). It follows that \({K_{m,n}}\) has \({m \times{} n}\) edges. (SOURCE)
12 In linear algebra, linear transformations can be represented by matrices. If \({T}\) is a linear transformation mapping \({\mathbf{R}^{n}}\) to \({\mathbf{R}^{m}}\) and \({{\vec{x}}}\) is a column vector with \({n}\) entries, then \({T( \vec{x} ) = \mathbf{A} \vec{x}}\) for some \({m\times{}n}\) matrix \({\mathbf{A}}\) called the transformation matrix of \({T}\). Note that \({\mathbf{A}}\) has \({m}\) rows and \({n}\) columns, whereas the transformation \({T}\) is from \({\mathbf{R}^{n}}\) to \({\mathbf{R}^{m}}\). (SOURCE)
13 Linear algebra is the branch of mathematics concerning linear equations such as \({a_{1}x_{1}+\cdots+a_{n}x_{n}=b}\), linear functions such as \({(x_{1},\ldots,x_{n})\mapsto{}a_{1}x_{1}+\ldots+a_{n}x_{n}}\) and their representations through matrices and vector spaces. (SOURCE)
14 Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables, rather than just one (SOURCE)
15 In mathematics, a real number is a value of a continuous quantity that can represent a distance along a line. The adjective real in this context was introduced in the 17th century by René Descartes, who distinguished between real and imaginary roots of polynomials. The real numbers include all the rational numbers, such as the integer \({−5}\) and the fraction \({4/3}\), and all the irrational numbers, such as \({\sqrt{2} = 1.41421356...}\), the square root of 2, an irrational algebraic number. Included within the irrationals are the transcendental numbers, such as \({\pi}\) = 3.14159265.... In addition to measuring distance, real numbers can be used to measure quantities such as time, mass, energy, velocity, and many more. (SOURCE)
16 In mathematics and in particular the mathematics of dynamical systems, discrete time and continuous time are two alternative frameworks within which to model variables that evolve over time. Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period") — that is, time is viewed as a discrete variable. (SOURCE)
17 The dynamical system concept is a mathematical formalization for any fixed "rule" that describes the time dependence of a point's position in its ambient space. A dynamical system has a state determined by a collection of real numbers, or more generally by a set of points in an appropriate state space. Small changes in the state of the system correspond to small changes in the numbers. The evolution rule of the dynamical system is a fixed rule that describes what future states follow from the current state. (SOURCE)
18 In the digital abstraction one interprets voltage values as binary values. The advantages of the digital model cannot be overstated; this model enables one to focus on the digital behavior of a circuit, to ignore analog and transient phenomena, and to easily build larger more complex circuits out of small circuits. The digital model together with a simple set of rules, called design rules, enable logic designers to design complex digital circuits consisting of millions of gates [38] (SOURCE)
19 Neurons are remarkable among the cells of the body in their ability to propagate signals rapidly over large distances. They do this by generating characteristic electrical pulses called action potentials: voltage spikes that can travel down nerve fibers. The study of neural coding involves measuring and characterizing how stimulus attributes, such as light or sound intensity, or motor actions, such as the direction of an arm movement, are represented by neuron action potentials or spikes. In order to describe and analyze neuronal firing, statistical methods and methods of probability theory and stochastic point processes have been widely applied. (SOURCE)
20 In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector. Single layer perceptrons are only capable of learning linearly separable patterns; in 1969 a famous — or some would say infamous — book entitled Perceptrons by Marvin Minsky and Seymour Papert [80] showed that it was impossible for these classes of network to learn an XOR function. (SOURCE)
21 In Euclidean geometry, linear separability is a property of a pair of sets of points. This is most easily visualized in two dimensions (the Euclidean plane) by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if line is replaced by hyperplane. (SOURCE)
22 Linear algebra is the branch of mathematics concerned with the study of vectors, vector spaces (also called linear spaces), linear transformations (also called linear maps), and systems of linear equations. Linear algebra is concerned with linear equations such as $${a_{1}x_{1}+\cdots+a_{n}x_{n}=b,}$$ and linear functions such as $${(x_{1},\ldots,x_{n})\mapsto{} a_{1}x_{1}+\ldots+a_{n}x_{n}}$$ and their representations through matrices and vector spaces. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. (SOURCE)
23 In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. Provided that they have the same size (each matrix has the same number of rows and the same number of columns as the other), two matrices can be added or subtracted element by element. The rule for matrix multiplication, however, is that two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second (i.e., the inner dimensions are the same, n for an (m×n)-matrix times an (n×p)-matrix, resulting in an (m×p)-matrix). There is no product the other way round, a first hint that matrix multiplication is not commutative. Any matrix can be multiplied element-wise by a scalar from its associated field. The individual items in an m×n matrix A, often denoted by \({a_{i,j}}\), where \({i}\) and \({j}\) usually vary from 1 to \({m}\) and \({n}\), respectively, are called its elements or entries. For conveniently expressing an element of the results of matrix operations the indices of the element are often attached to the parenthesized or bracketed matrix expression; e.g.: \({(AB)_{i,j}}\) refers to an element of a matrix product. In the context of abstract index notation this ambiguously refers also to the whole matrix product. (SOURCE)
24 In mathematics, a linear map (also called a linear mapping, linear transformation or, in some contexts, linear function) is a mapping \({V \mapsto{} W}\) between two modules (including vector spaces) that preserves (in the sense defined below) the operations of addition and scalar multiplication. Let \({V}\) and \({W}\) be vector spaces over the same field \({\mathbf{R}}\) where, for our purposes we take \({\mathbf{R}}\) to be the real numbers. A function \({f:V \mapsto{} W}\) is said to be a linear map if for any two vectors \({\mathbf{u}, \mathbf{v} \in{} \mathbf{R}}\) and any scalar \({c \in{} \mathbf{K}}\) the following two conditions are satisfied:
\({f(\mathbf{u} +\mathbf{v}) = f(\mathbf{u})+f(\mathbf{v})}\) — the operation of addition
\({f(c \mathbf{u}) = c f(\mathbf{u})}\) — the operation of scalar multiplication
Thus, a linear map is said to be operation preserving. In other words, it does not matter whether you apply the linear map before or after the operations of addition and scalar multiplication. From this it quickly follows that, the composition of linear maps is linear: if \({f : V \mapsto{} W}\) and \({g : W \mapsto{} Z}\) are linear, then so is their composition \({g \circ{} f : V \mapsto{} Z}\). (SOURCE)
25 The goal in machine learning is to construct algorithms that are able to learn to predict a certain target output. To achieve this, the learning algorithm is presented some training examples that demonstrate the intended relation of input and output values. Then the learner is supposed to approximate the correct output, even for examples that have not been shown during training. Without any additional assumptions, this problem cannot be solved exactly since unseen situations might have an arbitrary output value. The kind of necessary assumptions about the nature of the target function are subsumed in the phrase inductive bias. (SOURCE)
26 A differentiable function one real variable is a function whose derivative exists at each point in its domain. More generally, if \({x_{0}}\) is a point in the domain of a function \({f}\), then \({f}\) is said to be differentiable at \({x_{0}}\) if the derivative \({f′(x_{0})}\) exists. (SOURCE)
27 A discontinuity is point at which a mathematical object is discontinuous. Though defined identically, discontinuities of univariate functions are considerably different than those of multivariate functions. One of the main differences between these cases exists with regards to classifying the discontinuities, a caveat discussed more at length in the linked source. (SOURCE)
28 The function was named by Pierre Francois Verhulst, who studied it in relation to population growth. The initial stage of growth is approximately exponential (geometric); then, as saturation begins, the growth slows to linear (arithmetic), and at maturity, growth stops. It is thought Verhulst chose the term "logistic" in contrast to the logarithmic curve, and by analogy with arithmetic and geometric.TBD (SOURCE)
29 Stochastic gradient descent (often shortened to SGD), also known as incremental gradient descent, is an iterative method for optimizing a differentiable objective function, a stochastic approximation of gradient descent optimization. It is called stochastic because samples are selected randomly (or shuffled) instead of as a single group (as in standard gradient descent) or in the order they appear in the training set. (SOURCE)
30 In end-to-end reinforcement learning, the end-to-end process, in other words, the entire process from sensors to motors in a robot or agent involves a single, layered or recurrent neural network without modularization. The network is trained by reinforcement learning (RL). It was applied successfully in learning to play Atari video games and AlphaGo by Google DeepMind. It employs unsupervised learning and does not rely on having labeled data. (SOURCE)
31 In mathematical optimization, statistics, econometrics, decision theory, machine learning and computational neuroscience, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its negative (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. (SOURCE)
32 The gradient is a multi-variable generalization of the derivative. While a derivative can be defined on functions of a single variable, for functions of several variables, the gradient takes its place. The gradient is a vector-valued function, as opposed to a derivative, which is scalar-valued. Like the derivative, the gradient represents the slope of the tangent of the graph of the function. More precisely, the gradient points in the direction of the greatest rate of increase of the function, and its magnitude is the slope of the graph in that direction. The components of the gradient in coordinates are the coefficients of the variables in the equation of the tangent space to the graph. This characterizing property of the gradient allows it to be defined independently of a choice of coordinate system, as a vector field whose components in a coordinate system will transform when going from one coordinate system to another. (SOURCE)
33 The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. A simple example of such a problem is to find the curve of shortest length connecting two points. (SOURCE)
34 The weight update rule in batch mode simply substitutes the weighted sum of the gradient of the loss function over all of the training examples in the current batch: $${\mathbf{w}_{t+1}\,\colon{=}\,\mathbf{w}_{t} - \eta{} \sum_{i=1}^{n}\nabla{} \frac{L_{i}({w}_{t})}{n}}$$ where \({L_i}\) is the loss function with respect to the \({i}\)th example in the training data.
35 In deep learning, a convolutional neural network is a class of deep neural networks, most commonly applied to analyzing visual imagery. CNNs use a variation of multilayer perceptrons designed to require minimal preprocessing. Convolutional networks were inspired by biological processes in that the connectivity pattern between neurons resembles the organization of the animal visual cortex. Individual cortical neurons respond to stimuli only in a restricted region of the visual field known as the receptive field. The receptive fields of different neurons partially overlap such that they cover the entire visual field. CNNs often learn the filters that in traditional algorithms were hand-engineered. This independence from prior knowledge and human effort in feature design is a major advantage. (SOURCE)
36 Linearity is the property of a mathematical relationship or function which means that it can be graphically represented as a straight line. Examples are the relationship of voltage and current across a resistor (Ohm's law), or the mass and weight of an object. Proportionality implies linearity, but linearity does not imply proportionality. In mathematics, a linear map or linear function f(x) is a function that satisfies the following two properties:
Additivity: \({f(x + y) = f(x) + f(y)}\)
Homogeneity of degree 1: \({f(αx) = αf(x)}\) for all \({α}\).
The homogeneity and additivity properties together are called the superposition principle. The concept of linearity can be extended to linear operators. Important examples of linear operators include the derivative considered as a differential operator. When a differential equation can be expressed in linear form, it is generally straightforward to solve by breaking the equation up into smaller pieces, solving each of those pieces, and summing the solutions. (SOURCE)
37 Cosine similarity is a measure of similarity between two non-zero vectors of an inner product space that measures the cosine of the angle between them. The cosine of \({0^{\circ}}\) is 1, and it is less than 1 for any angle in the interval \({(0,\pi{}]}\) radians. It is thus a judgment of orientation and not magnitude: two vectors with the same orientation have a cosine similarity of 1, two vectors oriented at \({90^{\circ}}\) relative to each other have a similarity of 0, and two vectors diametrically opposed have a similarity of -1, independent of their magnitude. The cosine similarity is particularly used in positive space, where the outcome is neatly bounded in \({[0,1]}\). (SOURCE)
38 It is common to periodically insert a Pooling layer in-between successive Conv layers in a ConvNet architecture. Its function is to progressively reduce the spatial size of the representation to reduce the amount of parameters and computation in the network, and hence to also control overfitting. The Pooling Layer operates independently on every depth slice of the input and resizes it spatially, using the MAX operation. The most common form is a pooling layer with filters of size 2x2 applied with a stride of 2 downsamples every depth slice in the input by 2 along both width and height, discarding 75% of the activations. Every MAX operation would in this case be taking a max over 4 numbers (little 2x2 region in some depth slice). The depth dimension remains unchanged. (SOURCE)
39 Here is a somewhat more detailed — or at least more graphic — account of convolutional neural networks as they apply to computer vision and image processing:
| |
| Figure 3: The graphic on the left (a) illustrates the basic elements involved in convolving a \({3 \times{} 3}\) filter with a \({8 \times{} 8}\) matrix to compute a response matrix. The graphic on the right (b) depicts a typical application of convolution in the context of convolutional neural networks in which each filter in a bank of \({B}\) filters is convolved with an \({H \times{} W}\) image resulting in a \({H \times{} W \times{} B}\) stack of responses which is then convolved with a max pooling kernel. | |
|
|
A simple gray-scale image is generally implemented as a two-dimensional matrix. However, when an image is encoded as the input layer in an artificial neural network, it represents a vector in a vector space of dimension equal to the number of pixels in the image. When dealing with high-dimensional inputs such as images, it is impractical to connect all the units in the input layer to all of the units in, for example, a subsequent hidden layer.
Instead, we only connect each unit in the hidden layer to a local region of the input layer. The spatial extent of this connectivity is a hyperparameter called the receptive field or filter size of the units in the hidden layer. Substitute the word "neuron" for "unit" and the same terminology is applied to neural circuits, especially circuits organized as topographic maps such as are found in the retinotopic maps appearing in the ventral visual stream of mammalian neocortex.
The size of the hidden layer is determined by the receptive field and the spacing or stride between the local regions assigned to hidden units. In image processing, a kernel or convolution matrix is a small matrix that serves as a filter on the input image used for edge detection, image blurring and other transformations. These transformations are accomplished by means of a convolution between a kernel and an image. A collection of filters is called a filter bank.
The term filter kernel or kernel function is generally employed when discussing the obvious generalization of convolution. In many image processing tasks, the kernel function is the dot product of the convolution matrix and a filter-sized region of the target data, corresponding to a matrix, volume or other form of structured data. In a convolutional neural network the entries in the convolution matrix are free parameters that are learned via back propagation.
When computing the convolution of an image with a filter, we run a sliding window over the image, applying the kernel function to the kernel at each receptive-field-sized local region of the input layer as defined by the filter size and stride parameters, resulting a filtered image the same size as the hidden layer. The coordinates of the local regions constitute a grid spanning the input layer, a 2D grid in the case of simple gray-scale images or 3D grid in the case of mesoscale volumetric data.
40 An autoencoder is a type of artificial neural network used to learn efficient data encodings in an unsupervised manner. The aim of an autoencoder is to learn a representation (encoding) for a set of data, typically for dimensionality reduction. Along with the reduction side, a reconstructing side is learned, where the autoencoder tries to generate from the reduced encoding a representation as close as possible to its original input, hence its name. Recently, the autoencoder concept has become more widely used for learning generative models of data. (SOURCE)
41 In mathematics, an identity function, also called an identity relation or identity map or identity transformation, is a function that always returns the same value that was used as its argument. In the form of an equation, the function is given by \({f(x) = x}\). ()
42 Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. (SOURCE)
43 In physics, chemistry, and biochemistry, an energy landscape is a mapping of all possible conformations of a molecular entity, or the spatial positions of interacting molecules in a system, or parameters and their corresponding energy levels, typically Gibbs free energy. Geometrically, the energy landscape is the graph of the energy function across the configuration space of the system. The term is also used more generally in geometric perspectives to mathematical optimization, when the domain of the loss function is the parameter space of some system. (SOURCE)
44 In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum of reversible work that may be performed by a thermodynamic system at a constant temperature and pressure. According to the second law of thermodynamics, for systems reacting at a fixed temperature and pressure, there is a general natural tendency to achieve a minimum of the Gibbs free energy. (SOURCE)
45 The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is an abstract vector space possessing the structure of an inner product that allows length and angle to be measured. Figure 4.A displays a three-dimensional Hilbert space. The coordinates of the vector shown just happen to correspond to four fundamental constants: Archimedes constant (Pi) \({= 3.14159 \ldots{}}\), Euler's constant, \({e = 2.71828\,\ldots{}}\), Van der Pauw's constant \({= 4.53236 \ldots{}}\), and the square root of twice Pi times Euler's constant also referred to as the Square root of Tau \({\cdot{}e}\), \({= \sqrt{2\pi\cdot{}e} = 4.13273 \ldots{}}\).
46 Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets. Whereas many classes of convex optimization problems admit polynomial-time algorithms, mathematical optimization is in general NP-hard. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. (SOURCE)
47 A saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. (SOURCE)
48 Regularization is the process of adding information in order to solve an ill-posed problem or to prevent overfitting. An ill-posed problem is one that has multiple solutions or is highly sensitive with respect to its initial changes. A theoretical justification for regularization is that it attempts to impose Occam's razor — the assumption that simpler solutions tend to be correct — on the solution. From a Bayesian point of view, many regularization techniques correspond to imposing certain prior distributions on model parameters.
49 A strange loop is a cyclic structure that goes through several levels in a hierarchical system. It arises when, by moving only upwards or downwards through the system, one finds oneself back where one started. Strange loops may involve self-reference and paradox. The concept of a strange loop was proposed and extensively discussed by Douglas Hofstadter in Gödel, Escher, Bach, and is further elaborated in Hofstadter's book I Am a Strange Loop, published in 2007. (SOURCE)
50 A homunculus is a representation of a small human being. Popularized in sixteenth-century alchemy and nineteenth-century fiction, it has historically referred to the creation of a miniature, fully formed human. (SOURCE)
51 Cartesian theater is a derisive term coined by philosopher and cognitive scientist Daniel Dennett to refer pointedly to a defining aspect of what he calls Cartesian materialism, which he considers to be the often unacknowledged remnants of Cartesian dualism in modern materialist theories of the mind. (SOURCE)
52 The phrase intrapersonal communication refers to a communicator's internal use of language or thought. It can be useful to envision intrapersonal communication occurring in the mind of the individual in a model which contains a sender, receiver, and feedback loop. (SOURCE)
54 "The Unreasonable Effectiveness of Mathematics in the Natural Sciences" is the title of an article published in 1960 by the physicist Eugene Wigner. In the paper, Wigner observed that the mathematical structure of a physical theory often points the way to further advances in that theory and even to empirical predictions. Wigner begins his paper with the belief, common among those familiar with mathematics, that mathematical concepts have applicability far beyond the context in which they were originally developed. Based on his experience, he says "it is important to point out that the mathematical formulation of the physicist's often crude experience leads in an uncanny number of cases to an amazingly accurate description of a large class of phenomena". (SOURCE)
53 In a posting featured on his website, Andrej Karpathy comments on the "unreasonable effectiveness of recurrent neural networks" paraphrasing Eugene Wigner's comment regarding the effectiveness of mathematics in the natural sciences54. Karpathy has also produced a wonderfully illustrated and animated online tutorials clearly explaining the theoretical and practical issues involved in working with convolutional architectures. Andrej is himself a quintessential example of how enthusiastic neural network researchers enjoy teaching and giving back to the same community that accelerated their education. Andrej's website provides reviews, tutorials and commentary well worth checking out from time to time.
55 Norbert Wiener was an American mathematician and philosopher. He was a professor of mathematics at the Massachusetts Institute of Technology (MIT). A child prodigy, Wiener later became an early researcher in stochastic and mathematical noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems. Wiener is considered the originator of cybernetics, a formalization of the notion of feedback, with implications for engineering, systems control, computer science, biology, neuroscience, philosophy, and the organization of society. (SOURCE)
56 Cybernetics is a transdisciplinary approach for exploring regulatory systems—their structures, constraints, and possibilities. Norbert Wiener defined cybernetics in 1948 as "the scientific study of control and communication in the animal and the machine." Cybernetics is applicable when a system being analyzed incorporates a closed signaling loop—originally referred to as a "circular causal" relationship—that is, where action by the system generates some change in its environment and that change is reflected in the system in some manner (feedback) that triggers a system change. (SOURCE)
57 Sigmoid functions \({\sigma{}(x) = y}\) all have the same general form of a smooth step function with the step crossing at zero on the \({x}\) axis. However, in some cases, e.g, when employed as a binary switch or gate, they are scaled to the interval \({[0.0,\,1.0]}\) on the \({y}\) axis, while in others, e.g, where the value of activation function can be positive or negative, they are generally scaled to the interval \({[-1.0,\,1.0]}\).
58 The fixed-size stipulation can be relaxed for image data by resizing and padding so that the same filters / code book can be applied to any size or format image as long as long as the training data is representative of the target content.
59 Opinion mining (sometimes known as sentiment analysis or emotion AI) refers to the use of natural language processing, text analysis, computational linguistics, and biometrics to systematically identify, extract, quantify, and study affective states and subjective information. (SOURCE)
60 Charles Sanders Peirce was an American philosopher, logician, mathematician, and scientist who is sometimes known as "the father of pragmatism". He was educated as a chemist and employed as a scientist for 30 years. Today he is appreciated largely for his contributions to logic, mathematics, philosophy, scientific methodology, and semiotics, and for his founding of pragmatism. He saw logic as the formal branch of semiotics, of which he is a founder. (SOURCE)
61 Semiotics (also called semiotic studies) is the study of sign process (semiosis). It includes the study of signs and sign processes, indication, designation, likeness, analogy, allegory, metonymy, metaphor, symbolism, signification, and communication. The semiotic tradition explores the study of signs and symbols as a significant part of communications. Different from linguistics, semiotics also studies non-linguistic sign systems. (SOURCE)
62 In semiotics and linguistics, context refers to those objects or entities that surround a focal event. Context is a frame that surrounds the event and provides resources for its appropriate interpretation. In the theory of sign phenomena adapted from that of Charles Sanders Peirce, the concept of context is integral to the definition of the index, one of the three classes of signs defined by Peirce. An index is a sign which signifies by virtue of "pointing to" some component in its context, or in other words an indexical sign is related to its object by virtue of their co-occurrence within some kind of contextual frame. (SOURCE)
63 Word embedding is the collective name for a set of language modeling and feature learning techniques in natural language processing (NLP) where words or phrases from the vocabulary are mapped to vectors of real numbers. Conceptually it involves a mathematical embedding from a space with one dimension per word to a continuous vector space with a much lower dimension. In linguistics word embeddings were discussed in the research area of distributional semantics. It aims to quantify and categorize semantic similarities between linguistic items based on their distributional properties in large samples of language data. The underlying idea that "a word is characterized by the company it keeps" was popularized by Firth. (SOURCE)
64 In mathematics, a saddle point is a point on the surface of the graph of a function where the slopes in orthogonal directions are all zero, but which is not a local extremum of the function. The name derives from the fact that the prototypical example in two dimensions is a surface that curves up in one direction, and curves down in a different direction, resembling a riding saddle or a mountain pass between two peaks forming a landform saddle. In terms of contour lines, a saddle point in two dimensions gives rise to a contour graph or trace in which the contour corresponding to the saddle point's value appears to intersect itself.
65 The PDP books included many contributing author but David Rumelhart and Jay McClelland were the editors and primary instigators of the effort. The two completed volumes, Parallel Distributed Processing, Volume 1 — Explorations in the Microstructure of Cognition: Foundations [105] and Parallel Distributed Processing, Volume 2 — Explorations in the Microstructure of Cognition: Psychological and Biological Models [106] are are high on the list of must-read books for graduate students interested neural networks.
66 Single instruction, multiple data (SIMD) is a class of parallel computers with multiple processing elements that perform the same operation on multiple data points simultaneously. Such machines exploit data level parallelism, but not concurrency: there are simultaneous (parallel) computations, but only a single process (instruction) at a given moment. SIMD hardware is especially effective for speeding up vector processing and linear algebra applications that are important in accelerating neural networks well as the sort of computations that often dominate in multimedia applications such as graphics and image and audio compression.
67 This is a practical consideration and not a deep theoretical statement about computability or learnability. In the mathematical theory of artificial neural networks, the universal approximation theorem states that a feed-forward network with a single hidden layer containing a finite number of neurons can approximate continuous functions on compact subsets of \({\mathbf{R}^{n}}\), under mild assumptions on the activation function. The theorem thus states that simple neural networks can represent a wide variety of interesting functions when given appropriate parameters; however, it does not touch upon the algorithmic learnability of those parameters. Both feedforward and recurrent neural networks have been shown to be universal approximators under — what some theorists consider — reasonable assumptions. The implications of this (seemingly) distinction without a difference would take too long and are too complicated to cover thoroughly enough in this document. Here are two relevant papers [110, 119] with additional references to be found in their respective bibliographies.
68 Linear and Nonlinear Thinking
Carson Chow
October 2014
A linear system is one where the whole is precisely the sum of its parts. You can know how different parts will act together by simply knowing how they act in isolation. A nonlinear function lacks this nice property. For example, consider a linear function \({f(x)}\). It satisfies the property that \({f(a x + b y) = a f(x) + b f(y)}\). The function of the sum is the sum of the functions. One important point to note is that what is considered to be the paragon of linearity, namely a line on a graph, i.e. \({f(x) = mx + b}\) is not linear since \({f(x + y) = m (x + y) + b \neq{} f(x)+ f(y)}\). The \({y}\)-intercept \({b}\) destroys the linearity of the line. A line is instead affine, which is to say a linear function shifted by a constant. A linear differential equation has the form $${\frac{dx}{dt} = M x}$$ where \({x}\) can be in any dimension. Solutions of a linear differential equation can be multiplied by any constant and added together.
Linearity is thus essential for engineering. If you are designing a bridge then you simply add as many struts as you need to support the predicted load. Electronic circuit design is also linear in the sense that you combine as many logic circuits as you need to achieve your end. Imagine if bridge mechanics were completely nonlinear so that you had no way to predict how a bunch of struts would behave when assembled together. You would then have to test each combination to see how they work. Now, real bridges are not entirely linear but the deviations from pure linearity are mild enough that you can make predictions or have rules of thumb of what will work and what will not.
Chemistry is an example of a system that is highly nonlinear. You can’t know how a compound will act just based on the properties of its components. For example, you can’t simply mix glass and steel together to get a strong and hard transparent material. You need to be clever in coming up with something like gorilla glass used in iPhones. This is why engineering new drugs is so hard. Although organic chemistry is quite sophisticated in its ability to synthesize various compounds there is no systematic way to generate molecules of a given shape or potency. We really don’t know how molecules will behave until we create them. Hence, what is usually done in drug discovery is to screen a large number of molecules against specific targets and hope. I was at a computer-aided drug design Gordon conference a few years ago and you could cut the despair and angst with a knife.
That is not to say that engineering is completely hopeless for nonlinear systems. Most nonlinear systems act linearly if you perturb them gently enough. That is why linear regression is so useful and prevalent. Hence, even though the global climate system is a highly nonlinear system, it probably acts close to linear for small changes. Thus I feel confident that we can predict the increase in temperature for a 5% or 10% change in the concentration of greenhouse gases but much less confident in what will happen if we double or treble them. How linear a system will act depends on how close they are to a critical or bifurcation point. If the climate is very far from a bifurcation then it could act linearly over a large range but if we’re near a bifurcation then who knows what will happen if we cross it.
I think biology is an example of a nonlinear system with a wide linear range. Recent research has found that many complex traits and diseases like height and type 2 diabetes depend on a large number of linearly acting genes (see here). Their genetic effects are additive. Any nonlinear interactions they have with other genes (i.e. epistasis) are tiny. That is not to say that there are no nonlinear interactions between genes. It only suggests that common variations are mostly linear. This makes sense from an engineering and evolutionary perspective. It is hard to do either in a highly nonlinear regime. You need some predictability if you make a small change. If changing an allele had completely different effects depending on what other genes were present then natural selection would be hard pressed to act on it.
However, you also can’t have a perfectly linear system because you can’t make complex things. An exclusive OR logic circuit cannot be constructed without a threshold nonlinearity. Hence, biology and engineering must involve “the linear combination of nonlinear gadgets”. A bridge is the linear combination of highly nonlinear steel struts and cables. A computer is the linear combination of nonlinear logic gates. This occurs at all scales as well. In biology, you have nonlinear molecules forming a linear genetic code. Two nonlinear mitochondria may combine mostly linearly in a cell and two liver cells may combine mostly linearly in a liver. This effective linearity is why organisms can have a wide range of scales. A mouse liver is thousands of times smaller than a human one but their functions are mostly the same. You also don’t need very many nonlinear gadgets to have extreme complexity. The genes between organisms can be mostly conserved while the phenotypes are widely divergent.
P.S. Carson Chow is a senior investigator in the Laboratory of Biological Modeling, at the National Institute of Diabetes and Digestive and Kidney Diseases, NIH. He was formerly on the faculty of the mathematics department at the University of Pittsburgh, where he remains an adjunct professor. (SOURCE)
69 A system of linear equations (or linear system) is a collection of linear equations involving the same set of variables. Solving a system of linear equations has a complexity of at most \({O(n^3)}\). At least \({n^2}\) operations are needed to solve a general system of \({n}\) linear equations. (SOURCE)
70 Linear time-invariant (LTI) theory investigates the response of a linear and time-invariant system to an arbitrary input signal. A good example of LTI systems are electrical circuits that can be made up of resistors, capacitors, and inductors. (SOURCE)
71 An integer programming problem is an optimization problem in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints (other than the integer constraints) are linear. (SOURCE)
72 The relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable. This technique transforms an NP-hard optimization problem (integer programming) into a related problem that is solvable in polynomial time (linear programming). (SOURCE)
73 The "Sorcerer's Apprentice" is a symphonic poem by the French composer Paul Dukas, written in 1897. Subtitled "Scherzo after a ballad by Goethe", the piece was based on Johann Wolfgang von Goethe's 1797 poem of the same name. By far the most performed and recorded of Dukas's works, its most notable performance was conducted by Leopold Stokowski in the Walt Disney 1940 animated film "Fantasia" has led to the piece becoming widely known to audiences outside the classical concert hall.
74 Rich and Waters were circumspect about the near-term prospects for automated programming [103]. The abstract of Charlies Rich and Richard Waters original paper [102] on the Programmer's Apprentice project reads:
The long-term goal of the Programmer's Apprentice project is to develop a theory of how expert programmers analyze, synthesize, modify, explain, specify, verify, and document programs. The authors present their vision of the Programmer's Apprentice, the principles and techniques underlying it, and their progress toward it. The primary vehicle for this exposition is three scenarios illustrating the use of the Apprentice in three phases of the programming task: implementation, design, and requirements. The first scenario is taken from a completed working prototype. The second and third scenarios are the targets for prototype systems currently under construction.
75 Cognitive Neuroscience
July 21, 2017 - Neil Burgess - SOURCE
Neuroscientist Neil Burgess on the origin of neuroscience, drugs in clinical psychology, and the revolution in molecular biology
Neuroscience is the science of neurons which is the active component, or the component responsible for thinking, acting, and perceiving in our brains. For more than a century people have been studying neurons and working out the biology of neurons and how they work, and grow, and interact with each other. Often looking at experiments with slices of brain in a dish, working at how neurons work at the microscopic level. In parallel, also for more than a century there’s been the study of psychology and behavior, so how we behave, perceive and remember things, and how we act in our daily life. At a certain point, the neuroscience and the study of cognition started to become interrelated where people began to realize that our brains are what generates our behavior and that it’s the neurons are the key elements in our brains that do that.
Essentially the field of cognitive neuroscience slowly came into being where people began to study the basis in the behavior of individual neurons and systems of neurons within the brain, of our own actual behavior, thoughts, and cognition. There’s an intersection between sort of molecular, biological neuroscience and cognitive psychology, the study of behavior, which was called cognitive neuroscience. Early experiments by people recording from individual neurons in animals or perhaps studying how the damage to parts of the brain in human neurological patients related to behavior. For example, what you could and couldn’t do after you damaged a particular part of the brain or what particular neuron seemed to be representing in the brain – animal models, for example. This was the start of the area of cognitive neuroscience. Maybe in the late 60s – early 70s this became a real topic and slowly began to expand. By the 1990s it became a big topic, it became clear that nearly all psychology departments would need to have some understanding of the relationship to the brain of the cognitive things they studied. And nearly all systems neuroscience departments that were interested in the biology of neurons would need to know something about what they actually do, how they generate brains and behavior, and perception.
In the mid 90s the University College London decided to set up an institute of cognitive neuroscience, where we are now. In this country, it was the first institute of cognitive neuroscience to bring together people from psychology, neurology, and neuroscience. They could all be in the same building to try to understand what they had in common about their knowledge of how the brain worked and how it helped us to behave, perceive, remember, and think. Now there are many subfields within cognitive neuroscience. People are interested in how we perceive the world around us, interested in vision, hearing, touch, and also, of course, in action, how we move, motor neuroscience. In the middle people are interested in higher cognitive thought, for example, memory, planning, decision-making. The traditional psychology department would have an interest in all of these different areas. Now people are interested in how the brain generates these different aspects of cognition. We see cognitive neuroscience has interest in all these different areas, too. We see a particularly exciting generation of new ideas coming all the way from understanding how neurons in visual cortex represent what we’re seeing, pioneered by Hubel and Wiesel’s work in the 60s.
Going all the way through to motor neuroscience and understanding how activity of neurons in the motor cortex, for example, via the spine actually controls muscle contractions and allows us to move. Then in the middle there’s the enormous area of cognition between perception and action which includes how we remember things that have happened to us before and how that can inform what we’re going to do next, and how we can think about the future, plan we’re going to do. And I haven’t even mentioned language which for humans is a very important area, though it’s a little bit harder to study it in animals.
Nowadays we see people who’ve come into the field of cognitive neuroscience neither from a standard psychology background or from neurology, or, perhaps, biology. We do see people from all of these areas coming into cognitive neurosciense, but also people who studied physics or engineering. Make it easy for them to design experiments or use new technologies which are coming online. So one of the drivers of the expansion in cognitive neuroscience, as well as the realization that the brain was the key to understanding many aspects of behavior and cognition, is the advance of technology. We see that in many different areas.
For example, in basic neuroscience we see molecular biology and optogenetic techniques that allow us to affect the activity of patterns of different kinds of neurons within the brain and we can see how that plays out in behavior, and we can record from that kind of activity. And in human cognitive neuroscience, functional brain imaging has given us a window into looking at metabolic activity and how it varies across the brain while people are thinking about different things, or perceiving different things, or even acting, as long as they don’t move their head too much. So given this technological advance there is also a role for computer scientists and engineers and physicists and so on to come into this area to make the most of the new technology which is enabling new experiments and therefore enabling the whole field to continue to expand and make new discoveries. The big advances in cognitive neuroscience have come through people from different disciplines working together. Certainly, initially there weren’t really many departments of cognitive neuroscience and there weren’t students who trained in cognitive neuroscience. Obviously, cognitive scientists and neurologists, people who knew how to do functional neuroimaging, neuroscientists had to come together to interact, to explore new explanations that could be made of cognition and behavior given what we know about what’s happening in the brain. But that would sort of characterize the state of the field in the 1990s.
Now there are many cognitive neuroscience programs and there are students who have done degrees, or masters courses, or PhDs in cognitive neuroscience. So there are many sorts of modern researchers who perhaps would still consider themselves to be a psychologist, or a neuroscientist, or a physiologist. But now they’re able to use a range of techniques which allow them to study behavior and cognition at the same time as aspects of what’s happening in the brain. Nowadays, the modern cognitive neuroscientist is an interdisciplinary worker, but it’s becoming more of a mature field, so that you could say that you’re just a cognitive neuroscientist and that is your field.
There are several interesting developments in cognitive neuroscience at the moment which really exemplify the current direction of the field of understanding the brain and behavior. One of these is broadly mental health. For a long time, people understood psychiatry and clinical psychology in terms of treatments and drugs that happen to work and there’s a long history of experience with. But the actual mechanism of how that treatment actually changes the behavior or the aspects of cognition that are dysfunctional is not well understood, what that mechanism is not really known. Recently, there’s been a trend towards trying to understand what these mechanisms are both in healthy, normally processing people and how they’ve gone wrong in certain psychiatric or neurological conditions. So that we can try to understand behavioral interventions and pharmacological interventions in terms of the neural mechanisms that you want to restore or that you want to change back to how they should be. This area of mental health is becoming more of a science, more like neuroscience than a practical experience dependent field like medicine. That’s a big area in which there is a current advance.
The other end of the scale in which there’s a lot of advances, of course, is the revolution in molecular biology. The fact that we can now record and control the activity of neurons and synapses within the brain with great specificity, often in animal models, means that we can really investigate the neural mechanisms of cognition in a way that we could not before. So it’s possible to, for example, reactivate the neurons that were active in a particular situation and show that the mouse, in this case, thinks that it is back in that situation again. So the molecular biology has the technological advances has also made a big advance at the sort of microscopic level that informs cognition. Equally at the macroscopic level what goes wrong with global cognition is beginning to be understood in terms of the mechanisms that happen within the brain involving actual neurons and synapses.
The future for cognitive neuroscience is to make an actual practical impact on treatment in psychiatry, mental health, and neurology. Ideally, beginning to understand what the neural mechanisms are behind normal cognition and how aspects of cognition can go wrong should really begin to impact on treatment and therapy. The next ten years hopefully we’ll see a combination of mental health practices, psychiatry, and cognitive neuroscience, as we saw between psychology, cognitive science, and neuroscience in cognitive neurosciense. It will hopefully begin to put this kind of mental health medicine firm mechanistic background rather than having to rely essentially on treatments that we know work, but we don’t really know why they work.
Neil Burgess
Professor of Cognitive and Computational Neuroscience, University College London
76 Neuromodulation is the physiological process by which a given neuron uses one or more chemicals to regulate diverse populations of neurons. This is in contrast to (fast) synaptic transmission in which an axonal terminal secretes neurotransmitters to target fast-acting receptors of only one particular partner neuron. Neuromodulators are neurotransmitters that diffuse through neural tissue to affect slow-acting receptors of many neurons.
In both cases the transmitter acts on local postsynaptic receptors, but in neuromodulation, the receptors are typically G-protein coupled receptors while in classical chemical neurotransmission, they are ligand-gated ion channels. Neurotransmission that involves metabotropic receptors (like G-protein linked receptors) often also involves voltage-gated ion channels, and is relatively slow. Conversely, neurotransmission that involves exclusively ligand-gated ion channels is much faster. (SOURCE)
77 Dehaene et alDehaeneetalPNAS-98 distinguish two main computational spaces within the brain: "The first is a processing network, composed of a set of parallel, distributed and functionally specialized processors or modular sub-systems ranging from primary sensory processors (such as area V1) or unimodal processors (such as area V4), which combine multiple inputs within a given sensory modality, up to heteromodal processors (such as the visuo-tactile neurons in area LIP) that extract highly processed categorical or semantic information. Each processor is subsumed by topologically distinct cortical domains with highly-specific local or medium-range connections that encapsulate information relevant to its function.
The second computational space is a global workspace, consisting of a distributed set of cortical neurons characterized by their ability to receive from and send back to homologous neurons in other cortical areas horizontal projections through long-range excitatory axons (which may impinge on either excitatory or inhibitory neurons). Our view is that this population of neurons does not belong to a distinct set of cardinal brain areas but, rather, is distributed among brain areas in variable proportions."
Mortimer Mishkin in his 2006 interview for the Society for Neuroscience History of Neuroscience Archives suggests the alternative of using Cognitive for Declarative and Behavioral instead of Procedural makes more sense in talking about mouse studies. At the 00:27:00 mark in his interview he also employs Episodic versus Semantic distinction from Tulving [127, 126] and discuses the relationships: Perirhinal Cortex \({\rightarrow{}}\) Ventral Stream Inputs \({\rightarrow{}}\) Inferior Temporal Cortex and Parahippocampal Gyrus \({\rightarrow{}}\) Dorsal Stream Inputs \({\rightarrow{}}\) Posterior Parietal Cortex in talking about their work tracing visual stimuli back along the ventral visual path to the terminus of the ventral stream of visual areas.
79 See the segment starting at 00:40:30 minutes into Matt Botvinick's CS379C lecture entitled Prefrontal cortex as a meta-reinforcement learning system for the algorithmic insight connecting action selection in the basal ganglia to DeepMind's success applying reinforcement learning [134]. Figure 9 from [130] is an excellent supplement that completes the second pathway — referred to as the indirect pathway — shown in Figure 8 with dashed lines to indicate that it is not being fully explained in the text. There are also Khan Academy lessons on both the direct and Khan Academy indirect pathways.
| |
| Figure 9: The basal ganglia form anatomically and functionally segregated neuronal circuits with thalamic nuclei and frontal cortical areas. (a) The motor circuit involves the motor and supplementary motor cortices, the posterolateral part of the putamen, the posterolateral GPe and GPi, the dorsolateral STN, and the ventrolateral thalamus. (b) The associative loop and (c) the limbic loop connect the prefrontal and cingulate cortices with distinct regions within the basal ganglia and thalamus. In the STN, a functional gradient is found, with a motor representation in the dorsolateral aspect of the nucleus, cognitive–associative functions in the intermediate zone, and limbic functions in the ventromedial region. Via a 'hyperdirect' pathway, the STN receives direct projections from the motor, prefrontal and anterior cingulate cortices that can detect and integrate response conflicts. See text for abbreviations. — Volkman et al [130] | |
|
|
Here are BibTeX entries with abstracts for the most relevant papers mentioned in Matt Botvinick's lecture, including the Nature Neuroscience paper by DeepMind [134] and the 2001 Hochreiter et al [58] paper that helped to inspire the DM work:
@article{VolkmannetalNATURE_REVIEWS_NEUROLOGY-10,
author = {Volkmann, J. and Daniels, C. and Witt, K.},
title = {{N}europsychiatric effects of subthalamic neurostimulation in {P}arkinson disease},
journal = {Nature Reviews Neurology},
year = {2010},
volume = {6},
number = {9},
pages = {487-498},
abstract = {Neurostimulation of the subthalamic nucleus (STN) is an established treatment for motor symptoms in advanced Parkinson disease (PD), although concerns exist regarding the safety of this therapy in terms of cognitive and psychiatric adverse effects. The basal ganglia are considered to be part of distributed cortico-subcortical networks that are involved in the selection, facilitation and inhibition of movements, emotions, behaviors and thoughts. The STN has a central role in these networks, probably providing a global 'no-go' signal. The behavioral and cognitive effects observed following STN high-frequency stimulation (HFS) probably reflect the intrinsic role of this nucleus in nonmotor functional domains. Nevertheless, postoperative behavioral changes are seldom caused by such stimulation alone. PD is a progressive neurodegenerative disorder with motor, cognitive, behavioral and autonomic symptoms. The pattern of neurodegeneration and expression of these symptoms are highly variable across individuals. The preoperative neuropsychiatric state can be further complicated by sensitization phenomena resulting from long-term dopaminergic treatment, which include impulse control disorders, punding, and addictive behaviors (dopamine dysregulation syndrome). Finally, personality traits, the social environment, culture and learned behaviors might be important determinants explaining why behavioral symptoms differ between patients after surgery. Here, we summarize the neuropsychiatric changes observed after STN HFS and try to disentangle their various etiologies.}
}
@article{WangetalNATURE-NEUROSCIENCE-18,
author = {Wang, Jane X. and Kurth-Nelson, Zeb and Kumaran, Dharshan and Tirumala, Dhruva and Soyer, Hubert and Leibo, Joel Z. and Hassabis, Demis and Botvinick, Matthew},
title = {Prefrontal cortex as a meta-reinforcement learning system},
journal = {Nature Neuroscience},
year = {2018},
volume = {21},
issue = {6},
pages = {860-868},
abstract = "Over the past 20 years, neuroscience research on reward-based learning has converged on a canonical model, under which the neurotransmitter dopamine {\^a}??stamps in{\^a}?? associations between situations, actions and rewards by modulating the strength of synaptic connections between neurons. However, a growing number of recent findings have placed this standard model under strain. We now draw on recent advances in artificial intelligence to introduce a new theory of reward-based learning. Here, the dopamine system trains another part of the brain, the prefrontal cortex, to operate as its own free-standing learning system. This new perspective accommodates the findings that motivated the standard model, but also deals gracefully with a wider range of observations, providing a fresh foundation for future research.",
}
80 The hippocampus plays an important role in the transfer of information from short-term memory to long-term memory during encoding and retrieval stages. These stages need not occur successively, but are broadly divided in the neuronal mechanisms they require or even in the hippocampal areas they activate. According to Michael Gazzaniga, "encoding is the processing of incoming information that creates memory traces to be stored." There are two steps to encoding: acquisition and consolidation. During acquisition, stimuli are committed to short term memory. Consolidation is where the hippocampus along with other cortical structures stabilize an object within long term memory. (SOURCE)
81 For more detail on the role of the hippocampus in facilitating episodic memory see Randall O'Reilly's CS379C lecture entitled Programming in the Brain starting 00:34:30 and the related paper by O'Reilly and Frank [90]. If you prefer more visually stimulating learning aids then check this video produced at the University of British Columbia illustrating Donald O. Hebb's postulates as applied to learning in the hippocampus:
@book{Hebb_The_Organization_of_Behavior-1949,
author = {Hebb, Donald O.},
title = {The organization of behavior: {A} neuropsychological theory},
publisher = {Wiley},
address = {New York},
year = 1949,
abstract = {Donald Hebb pioneered many current themes in behavioural neuroscience. He saw psychology as a biological science, but one in which the organization of behaviour must remain the central concern. Through penetrating theoretical concepts, including the "cell assembly," "phase sequence," and "Hebb synapse," he offered a way to bridge the gap between cells, circuits and behaviour. He saw the brain as a dynamically organized system of multiple distributed parts, with roots that extend into foundations of development and evolutionary heritage. He understood that behaviour, as brain, can be sliced at various levels and that one of our challenges is to bring these levels into both conceptual and empirical register. He could move between theory and fact with an ease that continues to inspire both students and professional investigators. Although facts continue to accumulate at an accelerating rate in both psychology and neuroscience, and although these facts continue to force revision in the details of Hebb's earlier contributions, his overall insistence that we look at behaviour and brain together within a dynamic, relational and multilayered framework remains. His work touches upon current studies of population coding, contextual factors in brain representations, synaptic plasticity, developmental construction of brain/behaviour relations, clinical syndromes, deterioration of performance with age and disease, and the formal construction of connectionist models. The collection of papers in this volume represent these and related themes that Hebb inspired. We also acknowledge our appreciation for Don Hebb as teacher, colleague and friend.},
}
82 Memory consolidation is a category of processes that stabilize a memory trace after its initial acquisition. Consolidation is distinguished into two specific processes, synaptic consolidation, which is synonymous with late-phase long-term potentiation and occurs within the first few hours after learning, and systems consolidation, where hippocampus-dependent memories become independent of the hippocampus over a period of weeks to years. Recently, a third process has become the focus of research, reconsolidation, in which previously-consolidated memories can be made labile again through reactivation of the memory trace. (SOURCE)
83 Autoassociative memories are capable of retrieving a piece of data upon presentation of only partial information. Hopfield networks are recurrent artificial neural networks that have been shown to act as an autoassociative memory since they are capable of remembering data by observing a portion of that data. Hopfield networks can be trained with a variety of different learning methods including Hebbian learning which is often summarized as "neurons that fire together wire together". (SOURCE)
84 In neuroscience, long-term potentiation (LTP) is a persistent strengthening of synapses based on recent patterns of activity. These are patterns of synaptic activity that produce a long-lasting increase in signal transmission between two neurons. The opposite of LTP is long-term depression, which produces a long-lasting decrease in synaptic strength. It is one of several phenomena underlying synaptic plasticity, the ability of chemical synapses to change their strength. As memories are thought to be encoded by modification of synaptic strength, LTP is widely considered one of the major cellular mechanisms that underlies learning and memory. (SOURCE)
85 Memory reconsolidation is the process of previously consolidated memories being recalled and actively consolidated. It is a distinct process that serves to maintain, strengthen and modify memories that are already stored in the long-term memory. Once memories undergo the process of consolidation and become part of long-term memory, they are thought of as stable. However, the retrieval of a memory trace can cause another labile phase that then requires an active process to make the memory stable after retrieval is complete. It is believed that post-retrieval stabilization is different and distinct from consolidation, despite its overlap in function. (SOURCE)
86 O'Reilly et al [93] on Fodor and Pylsshyn's notion of the systematicity of classical symbol processing systems:
Fodor and Pylyshyn [40] make two central claims about what a classical symbol processing system must be capable of, which define a classical model:
Mental representations have combinatorial syntax and semantics. Complex representations ("molecules") can be composed of other complex representations (compositionality) or simpler "atomic" ones, and these combinations behave sensibly in terms of the constituents.
Structure sensitivity of processes. There is a separation between form and content, exemplified in the distinction between syntax and semantics, and processes can operate on the form (syntax) while ignoring the semantic content.
Taken together, these abilities enable a system to be fully systematic and compositional. Systematicity comes directly from the ability to process the form or structure of something, independent of its specific contents: if you can process sentences with a given syntax (e.g., Noun Verb Object) then you can process any constituent words in such sentences—you do not have to relearn the syntax all over again for each new word.
87 Graves et al [48] point out some interesting parallels between their implementation of the Differentiable Neural Computer model and the role of the hippocampus in storing and retrieving information in episodic memory:
Content lookup enables the formation of associative data structures; temporal links enable sequential retrieval of input sequences; and allocation provides the write head with unused locations. However, there are interesting parallels between the memory mechanisms of a DNC and the functional capabilities of the mammalian hippocampus. DNC memory modification is fast and can be one-shot, resembling the associative long-term potentiation of hippocampal CA3 and CA1 synapses. The hippocampal dentate gyrus, a region known to support neurogenesis, has been proposed to increase representational sparsity, thereby enhancing memory capacity: usage-based memory allocation and sparse weightings may provide similar facilities in our model.
88 In the mammalian brain, information pertaining to sensing and motor control is topographically mapped to reflect the intrinsic structure of that information required for interpretation. This was early recognized in the work of Hubel and Wiesel [65, 64] on the striate cortex of the cat and macaque monkey and in the work of Wilder Penfield [96] developing the idea of a cortical homunculus in the primary motor and somatosensory areas of the brain located between the parietal and frontal lobes of the primate cortex. Such maps have become associated with the theory of embodied cognition.
89 Here's what Daniel Jurafsky and James Martin have to say about grounding and dialogue [67]:
While this idea of speech acts is powerful, modern systems expand these early taxonomies of speech acts to better describe actual conversations. This is because a dialog is not a series of unrelated independent speech acts, but rather a collective act performed by the speaker and the hearer. In performing this joint action the speaker and hearer must constantly establish common ground (Stalnaker, 1978), the set of things that are mutually believed by both speakers.The need to achieve common ground means that the hearer must ground the speaker’s utterances. To ground means to acknowledge, to make it clear that the hearer has understood the speaker’s meaning and intention. People need closure or grounding for non-linguistic actions as well. For example, why does a well-designed elevator button light up when it’s pressed? Because this indicates to the elevator traveler that she has successfully called the elevator. Clark (1996) phrases this need for closure as follows, after Norman (1988):
Principle of closure. Agents performing an action require evidence, sufficient for current purposes, that they have succeeded in performing it.Grounding is also important when the hearer needs to indicate that the speaker has not succeeded. If the hearer has problems in understanding, she must indicate these problems to the speaker, again so that mutual understanding can eventually be achieved.
90 Here is the abstract syntax tree for Euclid's algorithm which is an efficient method for computing the greatest common divisor (GCD) of two numbers:
 |
91 While the apprentice operates directly on the AST representation of the code, the IDE can be designed to periodically coerce this representation into a syntactically-correct form, display the result as human-readable code, and display meaningful annotations that highlight program fragments relevant to the ongoing collaboration and track the apprentice's attention.
92 Terrence Deacon's Symbolic Species has substantially altered my views on the evolutionary origins of language [27] and his Incomplete Nature makes a good deal more sense to me as a naturalistic theory of intensionality and normative judgment [28] than any other such account I've encountered in print. I won't spend a lot of time discussing Deacon's ideas on language in this chapter since they appear elsewhere in this document, but I feel compelled to acknowledge my intellectual debt to his insights and scholarship.
93 There is a well known anecdote among Computer Vision researchers regarding how difficult CV is. You can hear it being repeated in university labs and lecture theatres across the world. I myself have heard it several times.
Computer Vision was originally a summer project given to an undergraduate student
If you look around you can find various versions of the same anecdote, and sometimes it even goes so far to suggest that the project was to solve the whole Computer Vision problem. Everyone has smiled and reflected that it's probably true. There are a lot of things like this that we accept unquestioningly. One day I was thinking to myself "how true is this story ?"
After fifteen minutes of searching with Google, the majority of web pages give a citation that the person who said this was Marvin Minsky and the student was Gerald Sussman. According to the majority of these quotes, in 1966 Minsky asked Sussman to "connect a camera to a computer and do something with it".
They may indeed have had that conversation but in actual fact, the original Computer Vision project referred to above was set up by Seymour Papert at MIT and given to Sussman who was to co-ordinate a group of 10 students including himself.
The original document outlined a plan to do some kind of basic foreground/background segmentation, followed by a subgoal of analysing scenes with simple non-overlapping objects, with distinct uniform colour and texture and homogeneous backgrounds. A further subgoal was to extend the system to more complex objects.
So it would seem that Computer Vision was never a summer project for a single student, nor did it aim to make a complete working vision system. Maybe it was too ambitious for its time, but it's unlikely that the researchers involved thought that it would be completely solved at the end. Finally, Computer Vision as we know it today is vastly different to what it was thought to be in 1966. Today we have many topics derived from CV such as inpainting, novel view generation, gesture recognition, deep learning, etc. SOURCE
94 Research on the function of the hippocampus in rodents has provided evidence of 'time cells' that provide a form of sequence memory that incorporates both time and space [72]. More recent research has identified human hippocampal cells in both CA1 and CA3 that support the incorporation of temporal duration information in human hippocampal long-term memory sequence representations providing evidence of a common hippocampal neural mechanism representing temporal information in episodic memory [124, 109]. Here are the relevant abstracts and citations:
@article{MacDonaldetalNEURON-11,
author = {MacDonald, C. J. and Lepage, K. Q. and Eden, U. T. and Eichenbaum, H.},
title = {Hippocampal 'time cells' bridge the gap in memory for discontiguous events},
journal = {Neuron},
volume = {71},
number = {4},
year = {2011},
pages = {737-749},
abstract = {The hippocampus is critical to remembering the flow of events in distinct experiences and, in doing so, bridges temporal gaps between discontiguous events. Here, we report a robust hippocampal representation of sequence memories, highlighted by "time cells" that encode successive moments during an empty temporal gap between the key events, while also encoding location and ongoing behavior. Furthermore, just as most place cells "remap" when a salient spatial cue is altered, most time cells form qualitatively different representations ("retime") when the main temporal parameter is altered. Hippocampal neurons also differentially encode the key events and disambiguate different event sequences to compose unique, temporally organized representations of specific experiences. These findings suggest that hippocampal neural ensembles segment temporally organized memories much the same as they represent locations of important events in spatially defined environments.}
}
@article{SalzetalJoN-16,
author = {Salz, Daniel M. and Tiganj, Zoran and Khasnabish, Srijesa and Kohley, Annalyse and Sheehan, Daniel and Howard, Marc W. and Eichenbaum, Howard},
title = {Time Cells in Hippocampal Area CA3},
journal = {Journal of Neuroscience},
volume = {36},
number = {28},
year = {2016},
pages = {7476-7484},
publisher = {Society for Neuroscience},
abstract = {Studies on time cells in the hippocampus have so far focused on area CA1 in animals performing memory tasks. Some studies have suggested that temporal processing within the hippocampus may be exclusive to CA1 and CA2, but not CA3, and may occur only under strong demands for memory. Here we examined the temporal and spatial coding properties of CA3 and CA1 neurons in rats performing a maze task that demanded working memory and a control task with no explicit working memory demand. In the memory demanding task, CA3 cells exhibited robust temporal modulation similar to the pattern of time cell activity in CA1, and the same populations of cells also exhibited typical place coding patterns in the same task. Furthermore, the temporal and spatial coding patterns of CA1 and CA3 were equivalently robust when animals performed a simplified version of the task that made no demands on working memory. However, time and place coding did differ in that the resolution of temporal coding decreased over time within the delay interval, whereas the resolution of place coding was not systematically affected by distance along the track. These findings support the view that CA1 and CA3 both participate in encoding the temporal and spatial organization of ongoing experience. Significance Statement: Hippocampal "time cells" that fire at specific moments in a temporally structured memory task have so far been observed only in area CA1, and some studies have suggested that temporal coding within the hippocampus is exclusive to CA1. Here we describe time cells also in CA3, and time cells in both areas are observed even without working memory demands, similar to place cells in these areas. However, unlike equivalent spatial coding along a path, temporal coding is nonlinear, with greater temporal resolution earlier than later in temporally structured experiences. These observations reveal both similarities and differences in temporal and spatial coding within the hippocampus of importance to understanding how these features of memory are represented in the hippocampus.},
}
@article{ThavabalasingametalPNAS-19,
author = {Thavabalasingam, Sathesan and O`Neil, Edward B. and Tay, Jonathan and Nestor, Adrian and Lee, Andy C. H.},
title = {Evidence for the incorporation of temporal duration information in human hippocampal long-term memory sequence representations},
journal = {Proceedings of the National Academy of Sciences},
publisher = {National Academy of Sciences},
year = {2019},
abstract = {We demonstrate that multivariate patterns of activity in the human hippocampus during the recognition and cued mental replay of long-term sequence memories contain temporal structure information in the order of seconds. By using an experimental paradigm that required participants to remember the durations of empty intervals between visually presented scene images, our study provides evidence that the human hippocampus can represent elapsed time within a sequence of events in conjunction with other forms of information, such as event content. Our findings complement rodent studies that have shown that hippocampal neurons fire at specific times during the empty delay between two events and suggest a common hippocampal neural mechanism for representing temporal information in the service of episodic memory. There has been much interest in how the hippocampus codes time in support of episodic memory. Notably, while rodent hippocampal neurons, including populations in subfield CA1, have been shown to represent the passage of time in the order of seconds between events, there is limited support for a similar mechanism in humans. Specifically, there is no clear evidence that human hippocampal activity during long-term memory processing is sensitive to temporal duration information that spans seconds. To address this gap, we asked participants to first learn short event sequences that varied in image content and interval durations. During fMRI, participants then completed a recognition memory task, as well as a recall phase in which they were required to mentally replay each sequence in as much detail as possible. We found that individual sequences could be classified using activity patterns in the anterior hippocampus during recognition memory. Critically, successful classification was dependent on the conjunction of event content and temporal structure information (with unsuccessful classification of image content or interval duration alone), and further analyses suggested that the most informative voxels resided in the anterior CA1. Additionally, a classifier trained on anterior CA1 recognition data could successfully identify individual sequences from the mental replay data, suggesting that similar activity patterns supported participants recognition and recall memory. Our findings complement recent rodent hippocampal research, and provide evidence that long-term sequence memory representations in the human hippocampus can reflect duration information in the order of seconds.},
}
95 Short-Term Versus Long-Term Memory
May 25, 2018 - Neil Burgess
Neuroscientist Neil Burgess on the difference between short-term and long-term memory, phonological loop, and amnesic people
Part of the reason for distinguishing short-term memory or working memory from long-term memory came from the 1950s, when people began to understand the nature of how memory depended on the brain. When Brenda Milner made her discovery with William Scoville that memory, being able to remember what had happened in the past essentially in terms of personal experience, was really strongly dependent on the hippocampus. When she studied a patient, who had had bilateral hippocampal removal, in the service of securing his epilepsy, she noticed that he was amnesic, he couldn’t remember what had happened to him in the past.
Interestingly, in subsequent experiments by her and other colleagues it was realized that there were many areas of preservation of memory in this kind of amnesic patient. Indeed he could remember semantic facts about the world, he found it difficult to learn new ones. He could remember the ones he already knew, he could learn new tasks like riding a bicycle, though that wasn’t the one they taught him. They taught him to do some tracing of shapes when looking in the mirror and this kind of things. He was able to do that kind of learning. Also his short-term memory seemed to be fine. So, it seems that this sort of short-term memory is different to the general memory or long-term memory where he can’t remember what happened to him in the days and weeks.
What we’ve learned from this is that there are probably neocortical mechanisms, parts of the brain outside of the hippocampus, which can support for a very short time certain kinds of information like a sequence of numbers or a sequence of locations, or a sequence of actions.
The distinction between short-term memory and long-term memory as originally made as: “Here’s a box that involves hippocampal system, in which we put our long-term memories for long-term storage and then here’s another box, which is somewhere else in the brain, perhaps in parietal and prefrontal areas, which we can store things for a short period of time”, that story is becoming a little bit more mixed now.
What we get is a picture, where different kinds of things are actually remembered in in slightly different ways. There seems to be some commonality in that. If you have to remember something for a long time, and if you’re going to be asked a long time later, which is no hope that you could keep this information active for that time, then you probably will depend on the hippocampal memory system. Amnesics won’t be able to remember that information, if it’s stuff that you have to actually remember the experience of seeing before. Whereas the actual mechanisms used for short periods of time or long periods of times may differ. They may depend on different parts of the brain, that may depend on the nature of the information that you’re trying to remember.
Neil Burgess
Professor of Cognitive and Computational Neuroscience, University College London
96 Episodic Memory
June 18, 2018 - Neil Burgess
Neuroscientist Neil Burgess on different types of memory, the H.M. patient case, and the role of hippocampus in recalling certain memories
Our record of our own personal experience is a crucial component of who we are, and defines in many ways how we see ourselves. This has come to be called episodic memory – our memory for our own personal experience. Over the last five or six decades we’ve begun to understand in increasing detail how episodic memory depends on the brain, and how the mechanisms in the brain allow us to remember what has happened to us.
This research had a great step forward in the 1950s, when Brenda Milner was studying patient Henry Molaison, after known as patient H.M., who had developed complete amnesia, following surgery to cure his intractable epilepsy, which removed parts of both of his hippocampi. The hippocampus is part of the brain in the middle of the temporal lobes, in here, which it’s often tends to be the focus for epilepsy. William Scoville, the neurosurgeon had removed the anterior part of both of his hippocampi to cure epilepsy.
The operation was successful in terms of treating the epilepsy, but, as Brenda Milner found out, he seemed to have lost all ability to form new memories. In fact, he had lost his ability to remember what had happened to him prior to the surgery going back many years. She referred to this loss of memory simply as loss of memory what the man in the street would call memory – the ability to remember what has happened to you.
Subsequent research much by herself and by other collaborators has come to specify in more detail the various different things that we can mean by memory. For example, semantic memory reflects your knowledge of facts and knowledge of how things are, whereas procedural memory relates to your ability to do things like riding a bicycle. The key aspect of episodic memory that seems to depend on the hippocampus Endel Tulving, the philosopher, characterized as an ability to re-experience what happened, so you can remember what you had for lunch yesterday, perhaps by thinking back and to some extent re-experiencing or imagining what happened. You can maybe imagine who was there and where you were, and what things look like, and what they tasted like. This re-experience is a characteristic of episodic memory. For, example you know some facts, but you don’t reinvent when you learned that fact, and you can ride a bicycle, but you may have forgotten the early experiences you had learning to do that. We knew from Brenda Milner’s work that episodic memory depends on the hippocampus. Over the years we’ve begun to make some progress in understanding what it is that happens in the brain, that enables episodic memory or this ability to re-experience what has happened to us in the past.
Much work, also concerning the hippocampus as it happened from neuroscientist in the early 1970s Tim Bliss and Terje Lomo, were interested in the electrical connections between neurons or the synaptic connections between neurons, which allow them to send little electrical signals to each other. It turned out – as had been predicted by Santiago Ramón y Cajal at the turn of the last century and Donald Hebb in around the 1950s – that if two neurons are both sending little electrical signals, and they have a connection between them, and this connection can get stronger. This is the ultimate basis of our ability to remember things.
If experiences are represented in the brain by these neurons sending little electrical signals to each other, then the pattern of activity across the neurons for a given event, perhaps when you’re eating your lunch the other day, that can be captured by strengthening the connections between all of the neurons that were active. In the sense that, if those connections have been strengthened now, at a later date, if I reactivate some of those neurons, perhaps by reminding you of the name of the person that you had lunch with, then those neurons can reactivate the other neurons via these strengthened connections, and therefore recreate, retrieve the pattern of activity that you had at the time. This brings us to the hippocampus.
As the mathematician David Marr pointed out in the early 1970s. The hippocampus being in the middle of the brain and getting input from all the different sensory areas for vision and touch, and hearing, and taste, and so on, is well positioned to make these changes in connection strength between neurons that could be representing the whole event of your having lunch yesterday. The visual input can drive some neurons from visual cortex, but eventually in the hippocampus itself, and the taste and sounds can drive other neurons to be active in the hippocampus, where they’re all close together, and all share a lot of potential connections. These connections can then be strengthened, so that you’ve laid down a memory for the event there of having lunch. Now, in future, if some of these neurons are reactivated, they can reactivate the other neurons, and they can in turn to reactivate neurons back in these sensory areas that can recreate the experience of the taste, and the sound, and the sights, and so on of that event.
Our basic model of episodic memory comes from this work by David Marr in the 1970s suggesting that the hippocampus contains this ability to reactivate the initial pattern that was stored when you experience the event. This can allow us to re-experience that event.
Some extra controversy about whether if you store a memory for a very long time, whether this still depends on the other campus, or whether other parts of the brain can actually slowly increase connections between appropriate neurons to do that task without the hippocampus. As I said at the beginning, that patient H.M. after he lost his hippocampus, still appeared to be able to remember some things from back before he had the surgery on his own hippocampus. It’s possible other parts of the brain can step in and help you to remember very old memories as well, but that’s our basic understanding of how episodic memory can work. When we start to think about the actual details of what happens when you try and re-experience what happened, it becomes clear that we need to understand how things are represented like the scene that you would have seen around you, when you’re having lunch. Through a series of different developments, understanding how neurons in the hippocampus and in surrounding areas can represent where you are, and how the environment is laid out around you, we can now begin to have a neural level mechanistic understanding of what happens when you use your episodic memory to remember what happened.
For example, place cells discovered by John O’Keefe indicate where you are and can be stored to indicate where you were, the pattern of activity can be stored to indicate where you were when you were having this lunch, or when whatever event it was happened. Head direction cells discovered by Jim Ranck also in the same memory system can represent which way you are facing. Again, if that activity can be stored via strengthening connections between neurons, as I described before. We can begin to see how, when you want to remember what happened, when you were having lunch, you can reactivate a representation of where you were, in which way you are facing. From there we activate a lot of other representations of information held in the brain near to hippocampus, such as where buildings were around you, and where objects were near to you. In that way you can build up an image of the spatial scene around you. We can understand how that process would happen at the level of individual neurons. We explained this in a computational model that I made with Sue Becker, who was visiting from Canada in 2001.
We can begin to understand what individual neurons are doing to enable you to reimagine what happened, or we experience event is how Endel Tulving would put it. Of course, it’s important to know that this is not exactly like we experience – it may be much less detailed, and indeed it might be incorrect. Our memory is notoriously fallible. When you try to remember what happened at lunch, you may get some aspects wrong, but this mechanism that we’ve identified, what it will do is make sure that of all the things that you could retrieve, all the kinds of information you could retrieve, is actually consistent with what you could experience from that location where you’re in.
Because of the connections between all the neurons representing information and the place cells, which are representing you being in that one location, and information that is consistent with you having a particular viewpoint by connections that have been strengthened to head direction cells that indicate a particular viewpoint. So, what this mechanism will do is enforce the creation of a coherent spatial scene around you, in your mind’s eye, when you imagine what happened. It may be filled in with bits of information that have been incorrectly retrieved and may not be veridical, but it explains how you imagine what happened before.
At the level of neurons, and, of course, other parts of the brain are involved, but particularly the parietal lobe at the back represents where things are left and right, and straight ahead of you. Indeed, if you want to make actions to tell you how to move left and right, and operate on the environment, whereas these memory representations in and around the hippocampus are more abstract -what is to the north, what was to the left, what was to the west, or so on. You have to translate that into what would have been left or right, if you given your facing direction, what was left and right of you, if I was facing north and there’s a building to the west, then it will be on my left, but if I was facing south and if I want to imagine facing south, then obviously I would imagine that building being on my right, when I make a visual image that I can use to imagine what had happened. We’re now able to sort of make a neurolevel computational model of exactly how we can retrieve the spatial scene around a given event, or indeed imagine a new spatial scene. We could construct a coherent spatial scene using these mechanisms even for something that hadn’t happened. If we want to imagine something happening in the future, perhaps to plan what we should do, we can perhaps imagine what it would be like, and then see if that was a good idea or not.
Colleagues here at UCL, Eleanor Maguire and Demis Hassabis, showed indeed in 2007 that patients with damage to hippocampus find it difficult to imagine coherent spatial scenes, showing that their deficit is not just in memory, but also in this ability to imagine coherent scenes of what could be around them. I think this, this work can lead on hopefully to making a more mechanistic understanding of what can go wrong, for example, in disorders of memory, like post-traumatic stress disorder, where we get these scenes or reactivations, or flashbacks which are not under our control, or indeed in Alzheimer’s disease, where other aspects of episodic memory seem to be some of the first things that we can no longer do, or perhaps even in in terms of schizophrenia and other disorders, where we might get hallucinations or incorrect perceptions or imaginations that don’t relate to what we want to imagine or what we should actually perceive.
Neil Burgess
Professor of Cognitive and Computational Neuroscience, University College London
97 Working memory is a cognitive system with a limited capacity that is responsible for temporarily holding information available for processing. Working memory is important for reasoning and the guidance of decision-making and behavior. Working memory is often used synonymously with short-term memory, but some theorists consider the two forms of memory distinct, assuming that working memory allows for the manipulation of stored information, whereas short-term memory only refers to the short-term storage of information. SOURCE
98 Spatial Navigation
December 19, 2016 - Neil Burgess
Neuroscientist Neil Burgess on the discovery of place cells, spatial memory, and experiments with functional neuroimaging
For all mobile organisms and particularly mammals, including ourselves, knowing where we are and being able to find a way around, find a way back to our home, for example, find a way out to resources like food is a crucial cognitive capability. And we’ve recently begun to understand what the neural basis of this kind of spatial navigation is: knowing where you are and knowing how to get to places that you need to get to. So we’re now beginning to really understand what happens in the brain that enables us to know where we are and know how to find a way around and remember where the important places for us are in the environment.
This breakthrough of understanding really began in the late sixties and early seventies with John O’Keefe here at UCL discovering place cells, neurons within the hippocampus, a part of the brain, in animal models like rats and mice. These neurons fire whenever the animal is in a particular part of its environment and a different neuron fires when it’s somewhere else. So together this big population of neurons, if you look at the activity as it varies as the animal moves around its environment, you can tell where the animal is, so which of the pace cells are firing – firing little electrical impulses to other neurons in the brain – that tells you where it is in the environment.
And those neurons are telling the rest of the brain as the animal moves around all the time where is it in its environment. Shortly after this discovery in the eighties, Jim Ranck and his colleagues in New York discovered head direction cells. They’re like a neural compass. The place cells are active according to where the animal is in its environment, head direction cells are active according to which way it’s facing. So it doesn’t matter where it is, just where it’s facing. A given head direction cell will fire whenever the animal is facing north, for example, wherever it is. A different one will fire when it’s facing a different direction, so across the population of head direction cells, the pattern of activity is telling the rest of the brain which way is the animal facing all the time as it’s moving around.
And then the third kind of spatial cell was discovered much more recently in 2005 by Moser in Norway and these are the grid cells. They’re a little bit like place cells in the sense that as the animal moves around its environment, a given cell will fire depending on the location of the animal, but a given place cell will fire whenever it enters any one of a series of locations that are distributed about the environment of an animal in a regular triangular array. It’s a very surprising thing to see given the complexity of behaviours these animals are wandering around. But a given place cell will fire whenever it goes into any of these locations organised in a triangular array across the environment. And a different grid cell will fire on a similar array of locations slightly shifted from the other cell.
So that together in a population of these grid cells, the activity will move from one to another as the animal moves around. And so again, like the place cells, they are telling the rest of the brain in a special kind of way where the animal is. You could work out where the animal is from what pattern of grid cell activity there is and these are found in the entorhinal cortex which is just next to the hippocampus and they project into where the place cells are in the hippocampus. But because they have this funny repeating regular pattern of firing in the world and each one has a shifted copy of that same firing pattern in terms of where the cell fires in the world, it’s easy to imagine that these cells could be updating their firing pattern across the population of grid cells according to the movement of the animal. So as the animal moves in one direction, the activity passes from one grid cell to the next one whose firing patterns are shifted relative to the first cell. And that will be true wherever it is in the environment because of this funny repeating firing patterns that these cells have. People think that these grid cells are a way of interfacing knowledge about self-motion of the animal, including humans, we think, with the representation of where that animal or person is within the world. So the place cells could tell you where you are and the grid cells could update that knowledge given that you know you’ve moved 10 meters to the north, for example, you now know where you should be given where you were and you’ve moved.
More recently still here we’ve found some cells which indicate our location relative to the environment around us — boundary vector cells. So whenever you have a large extended environmental feature there are cells again in the same area near the hippocampus which indicate that the animal or perhaps a person is a particular distance and direction from a big building or a large extended environmental feature and Colin Lever discovered these cells working with myself and John O’Keefe. And more recently, Jim Knierim in the United States has found cells which indicate the distance and direction of the animal from individual objects. So what we’re beginning to see altogether is that cells in and around the hippocampus in this part of the brain in humans that’s sort of in here – in the middle of the medial temporal lobes, all these different cells encoding for our location and our direction and being able to update their activity given our own movements and also cells representing where we are relative to environmental features or objects within our environment mean that we can understand really at the new level how we can know where we are and where other things are around us and where we’re heading.
And more important, perhaps for the idea of navigation and spatial memory is that’s it’s likely that these patterns of firing of neurons which define where we are and where everything in our environment is around us can be stored so if there is an important location, like your home, you can store the pattern of activity that indicates that location and now when you’re somewhere else, you could retrieve that pattern of activity and compare it to the current pattern of activity and work out the distance and direction between them so that you know how to get back to where you were if that’s where you want to go to. And one aspect about the regular repeating firing of the grid cells is that it’s a bit like a binary code it’s a very powerful code for potentially very large scale spaces so that if you know the firing of the grid cells across the population of grid cells at one location and also at your current location, you can work out the vector between them, the distance and direction between these locations even if they’re very far apart in principle. And so it could be that this system is a powerful way of knowing where you are and working out how to get to where you need to get to, which as I said is a very important property for most mobile organisms.
So looking into the future, hopefully beginning to understand the neural mechanisms behind the spatial memory will enable us to understand, for example, why people who start to get damage to this part of the brain, hippocampus, as in Alzheimer’s disease start to lose their way and start wandering off and getting lost which is a problem which creates great difficulties for their carers. Perhaps also it will become possible to make artificial devices – driverless car or robots that can find their way around in a similar way to humans, not necessarily because that’s the best way to find your way around if you’re a mechanical device that now may be more accurate but if artificial navigational devices can understand how humans find their way around then it makes them perhaps easier to interact with and they can have built-in knowledge of what kinds of aspects of finding our way around that humans find difficult and which they find easy.
So from all of these scientific experiments and developments, recently recognised for example with the 2014 Nobel Prize in physiology or medicine, we’ve got a nice detailed understanding of how these different types of neurons behave, but actually always a very simple circumstances in the lab so largely perhaps due to constraints of having simple understandable experiments and also constraints of being able to afford small amounts of lab space , most of these experiments are done in rather simple environments, rather small scale environments and it’s still an open question how this sort of representation of your location and direction and the grid cell firing patterns will really play out in the natural environment of a human in a complex city or a rat in a large-scale environment f many hundreds of meters with lots of complicated narrow roots and so on. And so although we’ve got a nice understanding of the simplest possible situation and what these neutrons are doing, it;s still not clear how this will play out in the complexity of everyday life and how it will really explain everyday navigation in complicated situations, but it’s a very good first step. So although most of these initial experiments have been done in rodents, we can now with functional neuroimaging look for the signs of the same kind of coding in the human brain. Often well people navigate in a virtual reality video game while their brain is being scanned and indeed we can make specific predictions of what kind of patterns of metabolic activity we should see in the scanner given that we know what the individual neurons should be doing if the person’s spatial memory is working like a rat’s or a mouse’s spatial memory. And perhaps surprisingly we’ve seen many strong complementary examples of the same kind of processing – you can see the evidence for the presence of place cells and head direction cells and grid cells and boundary vector cells, in fact, in a functional neuroimaging experiments with people exploring in virtual environments while the brain is being scanned and with epilepsy patients who have intractable epilepsy and need to have the focus of epilepsy actually removed from their brain, then electrical activity is recorded in many cases from these patients for many days and if they play a virtual reality video game where they virtually move around you can also see examples of recording of individual neurons that show where they were or which way they were headed in this virtual environment.
These experiments were done by Mike Kahana and Itzhak Fried largely and many collaborators. So although experiments are much easier to control perhaps and implement in rodents, mice, and rats that are foraging around for pieces of food, we can take those important results and work out what they imply for human experiments . And where we’ve looked we usually see something rather similar, of course in humans there is much more complexity there as well and all sorts of verbal representations and semantic knowledge and so on which we don’t usually study in rodents and in fact, would probably be impossible and that added on as well but these basic spatial building blocks that we see in rodents give us a starting point to look in humans and so far it seems like that’s a valid starting point.
Neil Burgess
Professor of Cognitive and Computational Neuroscience, University College London
99 A simple prototype implemented in Python for a dialog management system based on hierarchical planning is available here. This implementation focuses on the problem of interaction and negotiation during learning and understanding in continuous conversation. The repository also includes documentation in the form of a technical report that is also available on the Stanford course website here.
100 Here is a very brief summary of the different processes involved in human memory consolidation:
Memory consolidation is a category of processes that stabilize a memory trace after its initial acquisition.[1] Consolidation is distinguished into two specific processes, synaptic consolidation, which is synonymous with late-phase long-term potentiation and occurs within the first few hours after learning, and systems consolidation, where hippocampus-dependent memories become independent of the hippocampus over a period of weeks to years. Recently, a third process has become the focus of research, reconsolidation, in which previously-consolidated memories can be made labile again through reactivation of the memory trace. (SOURCE)
102 Following [29, 12], we employ hierarchical planning technology to implement several key components in the underlying bootstrapping and dialog management system. Each such component consists of a hierarchical task network (HTN) representing a collection of hierarchically organized plan schemas designed to run in a lightweight Python implementation of the HTN planner developed by Dana Nau et al [85]:
Hierarchical task network (HTN) planning is an approach to automated planning in which the dependency among actions can be given in the form of hierarchically structured networks. Planning problems are specified in the hierarchical task network approach by providing a set of tasks, which can be:
primitive tasks, that roughly correspond to the actions of STRIPS,
compound tasks, that can be seen as composed of a set of simpler tasks, and
objective tasks, that roughly correspond to the goals of STRIPS, but are more general.
A solution to an HTN problem is then an executable sequence of primitive tasks that can be obtained from the initial task network by decomposing compound tasks into their set of simpler tasks, and by inserting ordering constraints. SOURCE
101 Bootstrapping the programmer's apprentice: Basic cognitive bootstrapping and linguistic grounding
The programmer's assistant agent is designed to distinguish between three voices: the voice of the programmer, the voice of the assistant's automated tutor and its own voice. We could have provided an audio track to distinguish these voices, but since there only these three and the overall system can determine when any one of them is speaking, the system simply adds a few bits to each utterance as a proxy for an audio signature allowing the assistant to make such distinctions for itself. When required, we use the same signature to indicate which of the three speakers is responsible for changes to the shared input and output associated with the fully instrumented IDE henceforth abbreviated as FIDE — pronounced "/fee/'-/day/", from the Latin meaning: (i) trust, (ii) credit, (iii) fidelity, (iv) honesty. It will also prove useful to further distinguish the voice of the assistant as being in one of two modes: private, engaging in so-called inner speech that is not voiced aloud, and public, meaning spoken out loud for the explicit purpose of communicating with the programmer. We borrow the basic framework for modeling other agents and simple theory-of-mind from Rabinowitz et al [101].
The bootstrap statistical language model consists of an n-gram embedding trained on large general-text language corpus augmented with programming and software-engineering related text drawn from online forums and transcripts of pair-programming dialog. For the time being, we will not pursue the option of trying to acquire a large enough dialog corpus to train an encoder-decoder LSTM/GRU dialog manager / conversational model [129]. In the initial prototype, natural language generation (NLG) output for the automated tutor and assistant will be handled using hierarchical planning technology leveraging ideas developed in the CMU RavenClaw dialogue management system [12]102, but we have plans to explore hybrid natural language generation by combining hard-coded Python dialog agents corresponding to hierarchical task networks and differentiable dialogic encoder-decoder thought-cloud generators using a variant of pointer-generator networks as described by See et al [113].
Both the tutor and assistant NLG subsystems will rely on a base-level collection of plans — hierarchical task network (HTN) — that we employ in several contexts plus a set of specialized plans — an HTN subnetwork — specific to each subsystem. At any given moment in time, a meta control system [52] in concert with a reinforcement-learning-trained policy determines the curricular goal constraining the tutor's choice of specific lesson is implemented using a variant of the scheduled auxiliary control paradigm described by Riedmiller et al [104]. Having selected a subset of lessons relevant to the current curricular goal, the meta-controller cedes control to the tutor which selects a specific lesson and a suitable plan to oversee interaction with the agent over the course of the lesson.
Most lessons will require a combination of spoken dialogue and interactive signaling that may include both the agent and the tutor pointing, highlighting, performing edits and controlling the FIDE by executing code and using developer tools like the debugger to change state, set break points and single step the interpreter, but we're getting ahead of ourselves. The curriculum for mastering the basic referential modes is divided into three levels of mastery in keeping with Terrence Deacon's description [27] and Charles Sanders Peirce's (semiotic) theory of signs. The tutor will start at the most basic level, continually evaluating performance to determine when it is time to graduate to the next level or when it is appropriate to revert to an earlier level to provide additional training in order to master the less demanding modes of reference.
103 Bootstrapping the programmer's apprentice: Simple interactive behavior for signaling and editing:
In the first stage of bootstrapping, the assistant's automated tutor engages in an analog of the sort of simple signaling and reinforcement that a mother might engage in with her baby in order to encourage the infant to begin taking notice of its environment and participating in the simplest forms of communication. The basic exchange goes something like: the mother draws the baby's attention to something and the baby acknowledges by making some sound or movement. This early step requires that the baby can direct its gaze and attend to changes in its visual field.
In the case of the assistant, the relevant changes would correspond to changes in FIDE or the shared browser window, pointing would be accomplished by altering the contents of FIDE buffers or modifying HTML. Since the assistant has an innate capability to parse language into sequences of words, the tutor can preface each lesson with short verbal lesson summary, e.g., "the variable 'foo'", "the underlined variable", "the highlighted assignment statement", "the expression highlighted in blue". The implicit curriculum followed by the tutor would systematically graduate to more complicated language for specifying referents, e.g., "the body of the 'for' loop", "the 'else' clause in the 'conditional statement", "the scope of the variable 'counter'", "the expression on the right-hand side of the first assignment statement".
The goal of the bootstrap tutor is to eventually graduate to simple substitution and repair activities requiring a combination of basic attention, signaling, requesting feedback and simple edits, e.g., "highlight the scope of the variable shown in red", "change the name of the function to be "Increment_Counter", "insert a "for" loop with an iterator over the items in the "bucket" list", "delete the next two expressions", with the length and complexity of the specification gradually increasing until the apprentice is capable of handling code changes that involve multiple goals and dozens of intermediate steps, e.g., "delete the variable "Interrupt_Flag" from the parameter list of the function declaration and eliminate all of the expressions that refer to the variable within the scope of the function definition".
Note the importance of an attentional system that can notice changes in the integrated development environment and shared browser window, the ability to use recency to help resolve ambiguities, and emphasize basic signals that require noticing changes in the IDE and acknowledging that these changes were made as a means of signaling expectations relevant to the ongoing conversation between the programmer and the apprentice. These are certainly subtleties that will have to be introduced gradually into the curricular repertoire as the apprentice gains experience. We are depending on employing a variant of Riedmiller et al that will enable us to employ the FIDE to gamify the process by evaluating progress at different levels using a combination of general extrinsic reward and policy-specific intrinsic motivations to guide action selection [104].
Randall O'Reilly mentioned in his class presentation the idea that natural language might play an important role in human brains as an intra-cortical lingua franca. Given that one of the primary roles language serves is to serialize thought thereby facilitating serial computation with all of its advantages in terms of logical precision and combinatorial expression, projecting a distributed connectionist representation through some sort of auto encoder bottleneck might gain some advantage in combining aspects of symbolic and connectionist architectures. This also relates to O'Reilly’s discussion of the hippocampal system and in particular the processing performed by the dentate gyrus and hippocampal areas CA1 in CA2 in generating a sparse representation that enables rapid binding of arbitrary informational states and facilitates encoding and retrieving of episodic memory in the entorhinal cortex.
104 Bootstrapping the programmer's apprentice: Mixed dialogue interleaving instruction and mirroring:
Every utterance, whether generated by the programmer or the apprentice's tutor or generated by the apprentice either intended for the programmer or sotto voce for its internal record, has potential future value and hence it makes sense to record that utterance along with any context that might help to realize that potential at a later point in time. Endel Tulving coined the phrase episodic memory to refer to this sort of memory. We'll forgo discussion of other types of memory for the time being and focus on what the apprentice will need to remember in order take advantage of its past experience.
Here is the simplest, stripped-to-its-most-basic-elements scenario outlined in the class notes: (a) the apprentice performs a sequence of steps that effect a repair on a code fragment, (b) this experience is recorded in a sequence of tuples of the form (st,at,rt,st+1) and consolidated in episodic memory, (c) at a subsequent time, days or weeks later, the apprentice recognizes a similar situation and realizes an opportunity to exercise what was learned in the earlier episode, and (d) a suitably adapted repair is applied in the present circumstances and incorporated into a more general policy so that it can be applied in wider range circumstances.
The succinct notation doesn't reveal any hint of the complexity and subtlety of the question. What were the (prior) circumstances — st? What was thought, said and done to plan, prepare and take action — at? What were the (posterior) consequences — rt and st+1? We can't simply record the entire neural state vector. We could, however, plausibly record the information temporarily stored in working memory since this is the only information that could have played any substantive role — for better or worse — in guiding executive function.
We can't store everything and then carefully pick through the pile looking for what might have made a difference, but we can do something almost as useful. We can propagate the reward gradient back through the value- / Q-function and then further back through the activated circuits in working memory that were used to select ai and adjust their weights accordingly. The objective in this case being to optimize the Q-function by predicting the state variables that it needs in order to make an accurate prediction of the value of applying action at in st as described in Wayne et al [136].
Often the problem can be described as a simple Markov process and the state represented as a vector comprising of a finite number of state variables, st = ⟨ α0, α1, α2, α3, α4, α5, α6, α7 ⟩ , with the implicit assumption that the process is fully observable. More generally, the Markov property still holds, but the state is only partially observable resulting in a much harder class of decision problem known as a POMDP. In some cases, we can finesse the complexity if we can ensure that we can observe the relevant state variables in any given state, e.g., in one set of states it is enough to know one subset of the state variables, {⟨ α0, α1, α2, α3, α4, α5, α6, α7 ⟩ }, while in another set of states a different subset of state variables suffices, {⟨ α0, α1, α2, α3, α4, α5, α6, α7 ⟩ }. If you can learn which state variables are required and arrange to observe them, the problem reduces to the fully observed case.
There's a catch however. The state vector includes state variables that correspond to the observations of external processes that we have little or no direct control over as well as the apprehension of internal processes including the activation of subnetworks. We may need to plan for and carry out the requisite observations to acquire the external process state and perform the requisite computations to produce and then access the resulting internal state information. We also have the ability to perform two fundamentally different types of computation each of which has different strengths and weaknesses that conveniently complement the other.
The mammalian brain is optimized to efficiently perform many computations in parallel; however, for the most part it is not particularly effective dealing with the inconsistencies that arise among those largely independent computations. Rather than relying on estimating and conditioning action selection on internally maintained state variables, most animals rely on environmental cues — callsed affordances [46] — to restrict the space of possible options and simplify action selection. However, complex skills like programming require complex serial computations in order to reconcile and make sense of the contradictory suggestions originating from our mostly parallel computational substrate.
Conventional reinforcement learning may work for some types of routine programming like writing simple text-processing scripts, but it is not likely to suffice for programs that involve more complex logical, mathematical and algorithmic thinking. The programmer's apprentice project is intended as a playground in which to explore ideas derived from biological systems that might help us chip away at these more difficult problems. For example, the primate brain compensates for the limitations of its largely parallel processing approach to solving problems by using specialized networks in the frontal cortex, thalamus, striatum, and basal ganglia to serialize the computations necessary to perform complex thinking.
At the very least, it seems reasonable to suggest that we need cognitive machinery that is at least as powerful as the programs we aspire the apprentice to generate [42]. We need the neural equivalent of the [CONTROL UNIT] responsible for maintaining a [PROGRAM COUNTER] and the analog of loading instructions and operands into REGISTERS in the [ARITHMETIC AND LOGIC UNIT] and subsequently writing the resulting computed products into other registers or RANDOM ACCESS MEMORY. These particular features of the von Neumann architecture are not essential — what is required is a lingistic foundation that supports a complete story of computation and that is grounded in the detailed — almost visceral — experience of carrying out computations.
A single Q (value) function encoding a single action-selection policy with fixed finite-discrete or continuous state and action spaces isn't likely to suffice. Supporting compiled subroutines doesn't significantly change the picture. The addition of a meta controller for orchestrating a finite collection of separate, special-purpose policies adds complexity without appreciably adding competence. And simply adding language for describing procedures, composing production rules, and compiling subroutines as a Sapir-Whorf-induced infusion of ontological enhancement is — by itself — only a distraction. We need an approach that exploits a deeper understanding of the role of language in the modern age — a method of using a subset of natural language to describe programs in terms of narratives where executing such a program is tantamount to telling the story. Think about how human cognitive systems encode and serialize remembered stories, about programs as stories drawing on life experience by exploiting the serial nature of episodic memory, and about thought clouds that represent a superposition of eigenstates such that collapsing the wave function yields coherent narrative that serves as a program trace.
105 Bootstrapping the programmer's apprentice: Composite behaviors corresponding to simple repairs:
A software design pattern "is a general, reusable solution to a commonly occurring problem within a given context in software design. It is not a finished design that can be transformed directly into source or machine code. It is a description or template for how to solve a problem that can be used in many different situations. Design patterns are formalized best practices that the programmer can use to solve common problems when designing an application or system" — SOURCE. They are typically characterized as belonging to one of three categories: creational, structural, or behavioral.
I would like to believe that such patterns provide clear prescriptions for how to tackle challenging programming problems, but I know better. Studying such patterns and analyzing examples of their application to practical problems is an excellent exercise for both computer science students learning to program, and practicing software engineers wanting to improve their skills. That said, these design patterns require considerable effort to master and are well beyond what one might hope to accomplish in bootstrapping basic linguistic and programming skills. Indeed, mastery depends on already knowing — at the very least — the rudiments of these skills.
I'm willing to concede that mental software is not always expressed in language. For the programmer's apprentice, I'm thinking of encoding what is essentially static and syntactic knowledge about programs and programming using four different representations, and what is essentially dynamic and semantic knowledge in a family of structured representations that encode program execution traces of one sort or another. The four static / syntactic representations are summarized as follows:
(i) distributed (connectionist) representations of natural language as points in high-dimensional embedding spaces — thought clouds;
(ii) natural language transcripts of dialogical utterances / interlocutionary acts encoded as lexical token streams — word sequences;
(iii) programs in the target programming language represented as structured objects corresponding to augmented abstract syntax trees (ASTs)— the augmentations correspond to edges representing procedure calls, iteration and recursion resulting in directed acyclic graphs;
(iv) hierarchical plans corresponding to subnetworks of hierarchical task networks (HTNs) or, if you like, the implied representation of hierarchical plans encoded in value iteration networks [121] and goal-based policies [50]. I'm also thinking about encoding HTNs as policies using a variation on the idea of options [120] as described in Riedmiller et al [104];
The first entry (i) is somewhat misleading in that any one of the remaining three (ii-iv) can be represented as a point / thought cloud using an appropriate embedding method. Thought clouds are the Swiss Army knife of distributed codes. They represent a (constrained) superposition of possibilities allowing us to convert large corpora of serialized structures into point clouds that enable massively parallel search, and subsequently allow us to collapse the wave function, as it were, to read off solutions by re-serializing the distributed encoding of constraints that result from conducting such parallel searches.
I propose to develop encoders and decoders to translate between (serial) representations (ii-iv) where only a subset of conversions are possible or desirable given the expressivity of the underlying representation language. I imagine autoencoders with an information bottleneck that take embeddings of natural language descriptions as input and produces an equivalent HTN representation, combining a mixture of (executable) interlocutory and code synthesis tasks. The interlocutory tasks generate explanations and produce comments and specifications. The code-synthesis tasks serve to generate, repair, debug and test code represented in the FIDE.
Separately encoded embeddings will tend to evolve independently, frustrating attempts to combine them into composite representations that allow powerful means of abstraction. The hope is that we can use natural language as a lingua franca — a "bridge" language — to coerce agreement among disparate representations by forcing them to cohere along shared, possibly refactored dimensions in much the same way that trade languages serve as an expeditious means of exchanging information between scientists and engineers working in different disciplines or scholars who do not share a native language or dialect.
106 Here are some papers from Tetsuro Matsuzawa's lab describing these experiments and interpreting them in terms of the evolutionary origins of human cognition:
@article{MatsuzawaDEVELOPMENT-07,
author = {Tetsuro Matsuzawa},
title = {Comparative cognitive development},
journal = {Developmental Science},
volume = {10},
number = {1},
year = {2007},
pages = {97–103},
abstract = {This paper aims to compare cognitive development in humans and chimpanzees to illuminate the evolutionary origins of human cognition. Comparison of morphological data and life history strongly highlights the common features of all primate species, including humans. The human mother–infant relationship is characterized by the physical separation of mother and infant, and the stable supine posture of infants, that enables vocal exchange, face-to-face communication, and manual gestures. The cognitive development of chimpanzees was studied using the participation observation method. It revealed that humans and chimpanzees show similar development until 3 months of age. However, chimpanzees have a unique type of social learning that lacks the social reference observed in human children. Moreover, chimpanzees have unique immediate short-term memory capabilities. Taken together, this paper presents a plausible evolutionary scenario for the uniquely human characteristics of cognition.}
}
@incollection{MatsuzawaHUMAN-CONCEPTS-10,
title = {Cognitive development in chimpanzees: A trade-off between memory and abstraction?},
author = {Tetsuro Matsuzawa},
booktitle = {Oxford series in developmental cognitive neuroscience. The making of human concepts},
editor = {D. Mareschal and P. C. Quinn and S. E. G. Lea},
publisher = {Oxford University Press},
address = {New York, NY, US},
year = {2010},
pages = {227-244},
abstract = {This chapter suggests that the strong, near-photographic memory of chimps for number may be one manifestation of a more general characteristic of a representational system that provides extraordinarily detailed records of visual scenes. Such a system may be viewed as adaptive in a cognitive niche in which rapid, categorical decisions need to be made about objects encountered (e.g. ripe vs. unripe food, friend vs. foe). By contrast, the human cognitive niche emphasizes linguistic descriptions of events that capture an abstract gist which can be communicated to others. In this sense, chimps may be likened to humans with autism who display weak central coherence (i.e. an eye for detail, but without the corresponding big-picture idea).}
}
@article{SakaietalPLoS-17,
author = {Sakai, T. and Mikami, A. and Suzuki, J. and Miyabe-Nishiwaki, T. and Matsui, M. and Tomonaga, M. and Hamada, Y. and Matsuzawa, T. and Okano, H. and Oishi, K.},
title = {{D}evelopmental trajectory of the corpus callosum from infancy to the juvenile stage: {C}omparative {M}{R}{I} between chimpanzees and humans},
journal = {PLoS ONE},
year = {2017},
volume = {12},
number = {6},
pages = {e0179624},
abstract = {How brains develop during early life is one of the most important topics in neuroscience because it underpins the neuronal functions that mature during this period. A comparison of the neurodevelopmental patterns among humans and nonhuman primates is essential to infer evolutional changes in neuroanatomy that account for higher-order brain functions, especially those specific to humans. The corpus callosum (CC) is the major white matter bundle that connects the cerebral hemispheres, and therefore, relates to a wide variety of neuronal functions. In humans, the CC area rapidly expands during infancy, followed by relatively slow changes. In chimpanzees, based on a cross-sectional study, slow changes in the CC area during the juvenile stage and later have also been reported. However, little is known about the developmental changes during infancy. A longitudinal study is also required to validate the previous cross-sectional observations about the chimpanzee CC. The present longitudinal study of magnetic resonance imaging scans demonstrates that the CC development in chimpanzees and humans is characterized by a rapid increase during infancy, followed by gradual increase during the juvenile stage. Several differences between the two species were also identified. First, there was a tendency toward a greater increase in the CC areas during infancy in humans. Second, there was a tendency toward a greater increase in the rostrum during the juvenile stage in chimpanzees. The rostral body is known to carry fibers between the bilateral prefrontal and premotor cortices, and is involved in behavior planning and control, verbal working memory, and number conception. The rostrum is known to carry fibers between the prefrontal cortices, and is involved in attention control. The interspecies differences in the developmental trajectories of the rostral body and the rostrum might be related to evolutional changes in the brain systems.}
}
107 Examples of Emergent systems illustrate the kinds of feedback between individual elements of natural systems that can give rise to surprising ordered behavior. They also illustrate a clear trade-off between the number of elements involved in the emergent system and the complexity of their individual interactions. The more complex the interactions between elements, the fewer elements are needed for a higher-level phenomenon to emerge. Hurricanes and sand dunes form from vast numbers of very simple elements whereas even small groups of birds can exhibit flocking behavior. Hurricanes emerge from mutual positive feedback between wind, humidity, evaporation of warm surface waters and Coriolis effects. (SOURCE)
108 There are numerous examples in the history of science in which researchers become so entrenched in their theories that they feel that it is their right and responsibility to discourage other scientists working on alternative theories — in the sense of replacing entrenched dogma, or even orthogonal theories as in the case of discovering additional biochemical signalling pathways in the nervous system that depend on protein phosphorylation [49].
Dr. Paul Greengard, Professor of Molecular and Cellular Neuroscience at Rockefeller University, won the 2000 Nobel Prize in Physiology or Medicine for his work on the signaling pathways in the nervous system. He and his colleagues showed nerve cells communicate through either fast or slow synaptic transmission. In this 2012 interview, he discusses their discoveries and the resistance and skepticism they faced in publishing their results.
Nestler: I think it's hard for students in biomedical science today, who, by second nature, know that protein phosphorylation mediates so many different neural phenomena, to think back — not that long ago, really — to 30 or so years ago. You published a review in Science in 1978, which was one of the first times you proposed a diversity of kinases mediating a diversity of types of signals on many types of neural phenomena. Now, human genome sequencing has indicated that there are about 500 protein kinases. Do you want to comment on that perspective?Greengard: There are now more than 1,000 tyrosine protein kinases, which is one subclass. There's a lot of evidence accumulated, not only in our lab but in many other laboratories, and now with modern molecular biology we can knock out genes and mutate them and so on. The evidence has become incontrovertible, and now, as you say, it is second nature to people.
Nestler: It really has transformed the way young people approach a biological question because protein phosphorylation is almost a reflex in terms of a mechanism that's pursued.
Greengard: Yes. That has come a long way. At the time we started this work, it was accepted that the way neural cells communicate with each other was through neurotransmitter release, diffusion to the postsynaptic membrane to activate receptors, which were hypothetical when we started this. The debate as to whether synaptic transmission was a chemical process was a battle that went on for 40 years.
Very distinguished scientists such as [John C.] Eccles took a long time to accept it. He believed in electrical transmission, which was perfectly logical. The idea was that when the nerve impulse came down to the nerve ending, there was an electrical field generated by the nerve impulse that changed the membrane potential across the postsynaptic membrane and initiated or inhibited a postsynaptic response. But, as I said, this view was rejected by the chemical school. It was about this time we started our work, and at that time, many people still believed it was an electrical response: the opening of a voltage-gated ion channel that initiated the signal going down the postsynaptic cell.
An important discovery at the time was that acetylcholine acting on receptors opened up ion channels and induced a postsynaptic response. While implicating neurotransmitters, these studies were still perfectly compatible with what was known at the time, with the idea that all that was involved was a change in ion conductivity across the membrane and, therefore, an inhibitory or excitatory postsynaptic potential.
Again, as we discussed earlier, I thought it might be more complex and that it might be somewhat like hormones, and that turned out to be the case. You can see that both ideas were correct. You can think of that electrical signal as being how the fast excitatory neurotransmitter glutamate and the fast inhibitory neurotransmitter GABA produce their effects in brain. But there are over 100 — probably many, many more — neurotransmitter pathways that work through these very complicated signal transduction cascades involving a change in the level of the second messenger, activation of a protein kinase or a protein phosphatase, and a change in phosphorylation of a key substrate protein, which then produces or modifies an electrical or other physiological response.
110 David Mayfield owns Blue Ridge Life Science an investment firm specializing in early and mid-stage neuroscience. His grandfather Dr. Frank Mayfield was a famous neurosurgeon, scientific leader and entrepreneur in medical technology whose invention of the spring aneurysm clip has saved thousands of lives. David has taken another route to improving the lives of patients with debilitating neural disorders, driven in part by tragedies within his extended family, but he is no less passionate about the science than his grandfather. Both David and I are dismayed with the way in which current financial, medical and scientific incentives are misaligned. In his life and work, he has attempted to redress the negative consequences of this misalignment, often by drawing attention to relevant science and championing new opportunities for intervention. His crusade to promulgate research on microglia and related drug development is an example of the former. Full disclosure: Dr. Mayfield was my uncle, father figure and mentor at a crucial stage in my young life following the sudden death of my father, and so David, colloquially speaking, is my nephew, or, genealogically more precise, my cousin once removed.
111 There is a case to be made that funding through conventional life science VCs, or even midsize biotechs with bigger bank accounts, won't provide new experimental drugs (or their microglial targets) with the chance to succeed. The problem relates paradoxically to the experimental data which seem to show that some of these drugs are curative in such a wide range of CNS diseases and maladies, e.g., multiple sclerosis, anxiety, drug withdrawal syndromes, stroke, chronic neuropathic pain, retinal degeneration. An embarrassment of riches of sorts which is disabling for VCs and also for midsize biotechs who want their drug candidates focused on very narrow mechanisms of action, and very narrowly defined indications. But what if the embarrassment of riches were explained by the drug's impact on a pathological mechanism broadly shared by much of neurodevelopmental and neurodegenerative disease?
It turns out that doesn't matter. Even a potent and very successful biotech such as Biogen would rather have one drug which mitigates the severity of one orphan disease, than one drug which may prevent, mitigate the severity of, and possibly cure ten diseases / disorders afflicting hundreds of millions. Something to do, perhaps, with incentives, liquidity preferences, and appetite for risk built into the way VCs are funded and the way biotechs are publicly financed? One theory is that the phenomenon also relates to a confusion of the scientific methods of drug discovery with the biology of disease and its causes. Anyway, that's just a long winded way of saying that it is going to take a creative, non-conventional organization to translate the new science of microglia into therapies helping patients.
112 Ben Barres was a pioneer in the research on glia leading to the discovery of their dual role in the central nervous system. Beth Stevens was among his students and his lab was responsible for many of the important innovations enabling researchers to study glia and reveal their complex behavior. The Chan-Zuckerberg Initiative has created a program to fund early career awards (RFA) for research on neurodegeneration in honor of Barres work and life. Barres died on December 27, 2017 twenty months after being diagnosed with pancreatic cancer. He was 63. SOURCE
109 Science is a human endeavor and so scientific research is initiated, expedited and impeded by human motivations. Recent news concerning capital investments in biotechnology prompted me to think more deeply about some ideas relating to neuroscience that I've been working on for a couple of years now with my collaborator David Mayfield110. Here is an elevator-pitch-style dramatization intended to highlight the situation prompting my attention:
What if everything we think we know about the brain as a network computing device is wrong or at least missing one of the most important clues regarding how we learn and perform reliable computations with unreliable components?
What if we are blind to one of the most important factors required to understand and treat a broad spectrum of neurodegenerative diseases due to our misconceptions about how the brain computes and protects itself from pathogens?
What if many neuroscientists are ignorant or dismissive of the work and that by allowing such attitudes to persist we are wasting large amounts of money and intellectual capital working on models that are fundamentally flawed?
What if conventional life science VC firms and midsize biotechs are disinclined to invest in research111, preferring drugs that mitigate the severity of orphan diseases rather than curing dozens of maladies in millions of patients?
I believe the antecedents in the above statements are accurate. As a computational neuroscientist, the evidence is compelling. As a computer scientist, the computational model suggests fascinating algorithmic and architectural innovations. There are likely multiple targets of opportunity depending on whether one is interested in developing drugs, inventing novel machine-learning hardware or establishing the basic scientific foundations. If you want to understand the science, check out this recent review articles [108], and read David's short but highly informative research notes included below:
Lessons learned since the rediscovery of microglia in 2005: Microglia are the brain's principal immuno-competent cells making up roughly 10-15 percent of the CNS cell population. Prior to 2005, they were thought to play a largely quiescent, passive role under physiological conditions. As the brain's resident phagocytic immune cells, they could certainly be called into action, but — it was thought — only in response to an immune challenge to the brain caused by infection, injury, or established disease. In 2005, however, this dogma was challenged. [...]
Discovering the active role of microglia in healthy brain: The human brain is composed of two computers rather than one — a neuron-based digital machine built to compute the relevance of experience strictly in terms of what it already knows, and a microglia-based analog machine built to teach the digital machine how to compute differently given novel experiences it can detect but not yet understand. What the digital machine knows is stored in the relative strengths of the 100 trillion synapses through which pre-synaptic neurons send signals to their shared post synaptic partner. [...]
Summarizing David's review, microglia serve two very different roles in the adult brain. In a healthy adult brain, they enable synaptic plasticity and play a key role in learning. However, in responding to neural damage, they abandon their constructive role in learning, undergo a major morphological transformation and revert to immunological functions programmed into the immature cells prior to entering their final home in the developing brain.
In the best case scenario, microglial cells don't confuse the different circumstances that warrant these two roles. In the worst case, normal neural activity is mistaken for abnormal, microglia mount a phagocytic response to imagined pathogens and compromised cells, neural processes are stripped of their dendritic structure and rendered unable to perform their normal computational functions.
Prior to discovering the dramatic evidence of this dual role in 2005, researchers were aware that exposure to an immune challenge early in life (perinatal) — before microglia have fully adopted the transcriptional profile that enables them to function behind the blood brain barrier as specialized brain cells rather than peripheral macrophage cells — is predictive of cognitive decline and memory impairment late in life and its time of onset.
Later it was found that an ill-timed immune challenge during this sensitive perinatal window, is also an essential predisposing risk factor for the major neuro-developmental diseases and disorders of youth ranging from autism in toddlers, attention-deficit / hyperactivity disorder in children and schizophrenia and mood and addiction disorders in adolescence and young adulthood.
Putting these observations together, scientists looked for and found the signatures of microglial phagocytic damage in the brains of young patients with neuro-developmental disease and older patients with neuro-degenerative disorders including Parkinson's and Alzheimer's diseases. This brief summary of more than a decade of work by scores of scientists doesn't do justice to the richness of the case for this disease model [25, 71, 99].
Given that it is difficult if not impossible to avoid an unfortunate immune challenge during the critical window, this would be sad news indeed to a parent with a child having such a history, or anyone witnessing the symptoms of neuro-degenerative disease in themselves or a loved one were it not for their being some promising treatment options that could potentially provide protection across a broad spectrum of disorders [8, 7].
It turns out that a class of anxiolytic drugs marketed in France for more than three decades as a non-sedating, non-addicting alternative to the benzodiazepines has been shown to be an effective microglial modulator relevant to neuro-developmental and neuro-degenerative disease. Analogs of the original drug called etifoxine or ETX has been shown to modulate microglia activation in response to numerous models of immune challenge. While there are challenges ahead in evaluating efficacy, this is a promising sign that some form of treatment could soon be available for those afflicted.
Lectures:
| [1] |
Professor Ben Barres112 (Stanford University Departments of Neurobiology and Developmental Biology) January 2017. Broad Institute Lecture.
Role of Microglia Activated A1 Phenotype Astrocytes in Neurodegenerative Diseases Ranging from AD to ALS, MS, and Retinal Degeneration. [VIDEO]
|
| [2] |
Professor Staci Bilbo (Harvard University Program in Neuroscience) June 2014.
Lecture to the Canadian Autism Society. The Immune System and Neural Development: Implications for Neurodevelopmental Disorders. [VIDEO]
|
| [3] |
Professor Beth Stevens (Harvard University Program in Immunology) November 2016. Simon Foundation Lecture. On New Science of Microglia Function in the Healthy Developing and Mature Brain and the Implications for Autism and Schizophrenia. [VIDEO]
|
References: