

Figure 1: Hybrid Video Coder
All of today’s video coding standards such as H.263 or H.26L have the basic component of the hybrid video coder in common. As illustrated in figure 1, the encoder incorporates an entire decoder loop in order to predict the subsequent frame. The predicted frame is subtracted from the current frame resulting in a representation of the changes between the two consecutive frames. Under the assumption of error-free transmission the difference signal is sufficient for the decoder to restore the original video sequence. Therefore the transmitted bit stream contains the quantized DCT coefficients of this difference. Even in the case of error-free transmission the decoded video will incur errors for instance due to quantization. The problem of errors propagating through the prediction loop of the decoder can be circumvented by encoding not only the difference signal but the actual frame. These two coding modes are generally referred to as inter mode for encoding of the difference only and intra mode for encoding the whole frame. Figure 2 illustrates a possible sequence of I (intra) and P (inter) frames.

Figure 2: Possible sequence of I and P frames
The ratio of the number of I frames and P frames is mostly fixed in advance. Often not the entire frame needs to be refreshed, but only small areas which encountered heavy motion for example, or other rapid changes. For this purpose the image is subdivided into smaller structures than frames such as blocks (8x8 pixels), macro blocks (2x2 blocks) and GOB (Group of Blocks) containing one row of macro-blocks. The relationship among these structures is illustrated in figure 3.
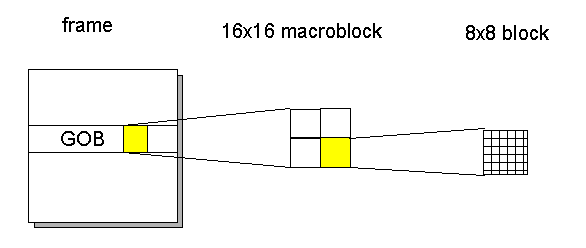
Figure 3: Structure of a H.263 frame
The architecture of P frames allows selection of the coding mode for each macro-block individually. The crucial question, however, is how to choose this mode. Generally speaking the solution is a trade-off between higher bit rate and low error vulnerability on the one hand and low bit rate at the expense of possible error propagation on the other hand. The problem can be formulated using a Lagrangian cost function:
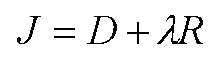
R denotes the bit rate whereas D is a measure of distortion, in our case the sum of squared differences. The parameter lambda is fixed to the empirically derived number 0.85 multiplied by the square of the quantization step size. The cost of each of the two encoding modes is calculated and the mode with the lower cost is chosen. Unlike quantization errors which are captured by the feedback loop in the encoder any errors occurring during transmission remain unconsidered in a conventional setup. We therefore propose to simulate various error patterns and their affect on the distortion encountered by the decoder before actually encoding the final bit stream. This approach is justified by two main observations:
The loss of some macro-blocks causes higher distortion at the receiver than of others due to error concealment.
The ratio of I to P frames is almost intuitively dependent on the error probability of the transmission channel.