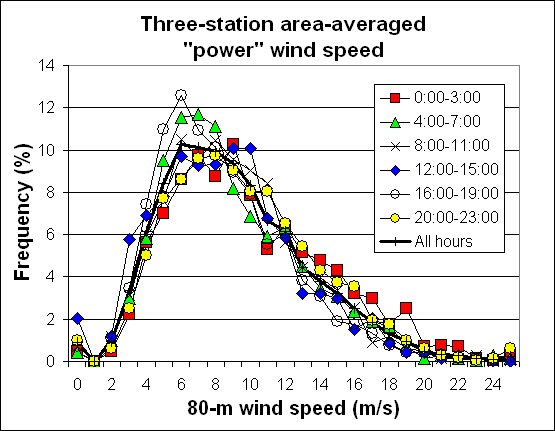
Legend:
Legend:
 |
speed<5.9 m/s (class 1 at 80 m) |
|---|---|
 |
5.9<=speed<6.9 m/s (class 2 at 80 m) |
 |
6.9<=speed<7.5 m/s (class 3 at 80 m) |
 |
7.5<=speed<8.1 m/s (class 4 at 80 m) |
 |
8.1<=speed<8.6 m/s (class 5 at 80 m) |
 |
8.6<=speed<9.4 m/s (class 6 at 80 m) |
 |
speed>=9.4 m/s (class 7 at 80 m) |
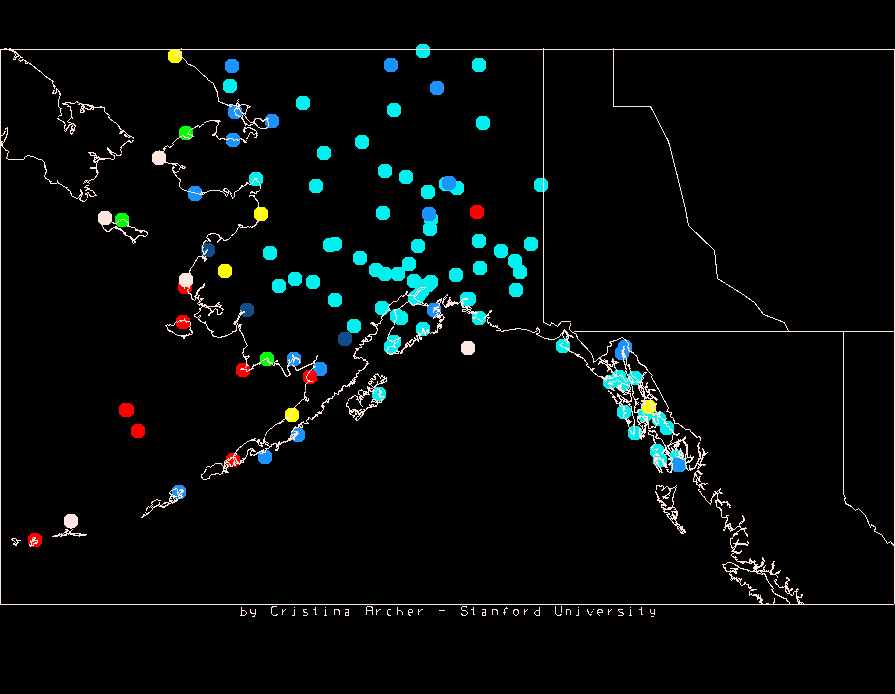
Alaska |
Hawaii |
||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
||||||||||||||||||||||||||||||||
| Postscript version available here | Postscript version available here | ||||||||||||||||||||||||||||||||
|
|
| State | Total No. of stations | No. of Class >=3 stations | Percent of Class >=3 stations | No. of coastal/offshore stations | No. of coastal/offshore class >=3 stations | Percent of coastal/offshore class >=3 stations | Percent of class >=3 stations that are coastal/offshore |
| Alaska | 144 | 37 | 25.7 | 78 | 30 | 38.5 | 81.1 |
| Texas | 87 | 31 | 35.6 | 10 | 9 | 90.0 | 29.0 |
| Kansas | 29 | 21 | 72.4 | 0 | 0 | 0.0 | 0.0 |
| Nebraska | 30 | 23 | 76.7 | 0 | 0 | 0.0 | 0.0 |
| Minnesota | 73 | 20 | 27.4 | 0 | 0 | 0.0 | 0.0 |
| Oklahoma | 24 | 19 | 79.2 | 0 | 0 | 0.0 | 0.0 |
| Iowa | 47 | 17 | 36.2 | 0 | 0 | 0.0 | 0.0 |
| South Dakota | 22 | 12 | 54.5 | 0 | 0 | 0.0 | 0.0 |
| Florida | 66 | 7 | 10.6 | 39 | 5 | 12.8 | 71.4 |
| California | 110 | 7 | 6.4 | 40 | 1 | 2.5 | 14.3 |
| New York | 37 | 7 | 18.9 | 8 | 5 | 62.5 | 71.4 |
| North Dakota | 12 | 8 | 66.7 | 0 | 0 | 0.0 | 0.0 |
| Ohio | 30 | 8 | 26.7 | 0 | 0 | 0.0 | 0.0 |
| North Carolina | 38 | 8 | 21.1 | 11 | 7 | 63.6 | 87 | .5
| Virginia | 41 | 6 | 14.6 | 7 | 2 | 28.6 | 33.3 |
| Missouri | 20 | 6 | 30.0 | 0 | 0 | 0.0 | 0.0 |
| Lousiana | 29 | 6 | 20.7 | 7 | 4 | 57.1 | 66.7 |
| New Jersey | 12 | 5 | 41.7 | 4 | 2 | 50.0 | 40.0 |
| Massachussetts | 21 | 6 | 23.8 | 11 | 4 | 36.4 | 80.0 |
| Connecticut | 8 | 3 | 37.5 | 3 | 3 | 100.0 | 100.0 |
| Washington | 41 | 3 | 7.3 | 12 | 2 | 16.7 | 66.7 |
| Maryland | 11 | 3 | 27.3 | 6 | 2 | 33.3 | 66.7 |
| Delaware | 3 | 1 | 33.3 | 1 | 1 | 100.0 | 100.0 |
| Rhode Island | 5 | 2 | 40.0 | 4 | 2 | 50.0 | 100. | 0
| Hawaii | 20 | 1 | 5.0 | 19 | 1 | 5.3 | 100.0 |
| Alabama | 22 | 1 | 4.5 | 2 | 1 | 50.0 | 100.0 |
| South Carolina | 18 | 1 | 5.6 | 4 | 1 | 25.0 | 100.0 |
| Pacific Islands | 8 | 6 | 75.0 | 8 | 6 | 75.0 | 100.0 |
| Buoys | 51 | 44 | 86.3 | 51 | 44 | 86.3 | 100.0 |
| Other states | 625 | 33 | 5.3 | 18 | 2 | 11.1 | 6.1 |
| Total U.S. | 1684 | 351 | 20.8 | 343 | 134 | 39.1 | 38.2 |
| Region | Total | Wind Class at 80 m | |||||||||||||||
| 1 | 2 | 3 | 3 | 5 | 6 | 7 | >=3 | ||||||||||
| V< 5.9 m/s | 5.9<=V< 6.9 m/s | 6.9<=V< 7.5 m/s | 7.5<=V< 8.1 m/s | 8.1<=V< 8.6 m/s | 8.6<=V< 9.4 m/s | V>=9.4 m/s | V>=6.9 m/s | ||||||||||
| # | # | % | # | % | # | % | # | % | # | % | # | % | # | % | # | % | |
| North-West | 231 | 209 | 90.5 | 14 | 6.1 | 4 | 1.7 | 1 | 0.4 | 1 | 0.4 | 1 | 0.4 | 1 | 0.4 | 8 | 3.5 |
| North-Central | 180 | 45 | 25.0 | 55 | 30.6 | 30 | 16.7 | 30 | 16.7 | 11 | 6.1 | 1 | 0.6 | 0 | 0.0 | 80 | 44.4 |
| Great Lakes | 161 | 89 | 55.3 | 53 | 32.9 | 13 | 8.1 | 3 | 1.9 | 2 | 1.2 | 1 | 0.6 | 0 | 0.0 | 19 | 11.8 |
| North-East | 147 | 80 | 54.4 | 38 | 25.9 | 14 | 9.5 | 9 | 6.1 | 3 | 2.0 | 2 | 1.4 | 1 | 0.7 | 29 | 19.7 |
| East-Central | 128 | 95 | 74.2 | 15 | 11.7 | 11 | 8.6 | 3 | 2.3 | 1 | 0.8 | 0 | 0.0 | 3 | 2.3 | 18 | 14.1 |
| South-East | 155 | 124 | 80.0 | 22 | 14.2 | 3 | 1.9 | 0 | 0.0 | 3 | 1.9 | 3 | 1.9 | 0 | 0.0 | 9 | 5.8 |
| South-Central | 213 | 82 | 38.5 | 47 | 22.1 | 28 | 13.1 | 25 | 11.7 | 17 | 8.0 | 8 | 3.8 | 6 | 2.8 | 84 | 39.4 |
| Southern Rockies | 112 | 87 | 77.7 | 16 | 14.3 | 1 | 0.9 | 7 | 6.3 | 0 | 0.0 | 1 | 0.9 | 0 | 0.0 | 9 | 8.0 |
| South-West | 131 | 115 | 87.8 | 9 | 6.9 | 3 | 2.3 | 3 | 2.3 | 1 | 0.8 | 0 | 0.0 | 0 | 0.0 | 7 | 5.3 |
| Alaska | 144 | 88 | 61.1 | 19 | 13.2 | 8 | 5.6 | 8 | 5.6 | 7 | 4.9 | 11 | 7.6 | 3 | 2.1 | 37 | 25.7 |
| Hawaii | 20 | 14 | 70.0 | 5 | 25.0 | 0 | 0.0 | 0 | 0.0 | 1 | 5.0 | 0 | 0.0 | 0 | 0.0 | 1 | 5.0 |
| Pacific Islands | 11 | 3 | 27.3 | 2 | 18.2 | 1 | 9.1 | 2 | 18.2 | 1 | 9.1 | 2 | 18.2 | 0 | 0.0 | 6 | 54.5 |
| Buoys | 51 | 4 | 7.8 | 3 | 5.9 | 3 | 5.9 | 3 | 5.9 | 2 | 3.9 | 11 | 21.6 | 25 | 49.0 | 44 | 86.3 |
| Total U.S. | 1684 | 1035 | 61.5 | 298 | 17.7 | 127 | 7.5 | 94 | 5.6 | 50 | 3.0 | 41 | 2.4 | 39 | 2.3 | 351 | 20.8 |
| Station | State | Annual Mean Speed (m/s) | Annual Wind Standard Deviation (m/s) | Wind Power Class | Annual Mean Wind Power (W/m²) | Annual Power Standard Deviation (W/m²) | ||||||||||
| Paper | A | abs(A) | Paper | A | abs(A) | Paper | A | abs(A) | Paper | A | abs(A) | Paper | A | abs(A) | ||
| AMA | TX | 10.3 | 8.8 | 8.8 | 4.9 | 4.5 | 4.5 | 7 | 6 | 6 | 1169 | 819 | 808 | 1899 | 1847 | 1846 |
| CAO | NM | 10.1 | 8.8 | 8.7 | 5.9 | 5.5 | 5.4 | 7 | 6 | 6 | 1437 | 1054 | 1020 | 4093 | 2761 | 2884 |
| CDB | AK | 13.6 | 10.7 | 10.7 | 8.5 | 6.6 | 6.7 | 7 | 7 | 7 | 3766 | 1847 | 1843 | 7607 | 4317 | 4359 |
| CSM | OK | 10.8 | 9.3 | 9.3 | 5.5 | 4.6 | 4.6 | 7 | 6 | 6 | 1463 | 893 | 984 | 2455 | 1393 | 1407 |
| DDC | KS | 10.1 | 8.7 | 8.6 | 5.4 | 4.8 | 4.6 | 7 | 6 | 6 | 1242 | 845 | 802 | 2414 | 2090 | 2049 |
| GCK | KS | 9.9 | 8.6 | 8.5 | 5.6 | 4.8 | 4.7 | 7 | 6 | 5 | 1304 | 851 | 813 | 3297 | 2574 | 2539 |
| GDP | TX | 14.8 | 14.2 | 14.2 | 8.7 | 8.8 | 8.8 | 7 | 7 | 7 | 4476 | 4306 | 4326 | 8804 | 9661 | 9707 |
| HBR | OK | 10.8 | 9.3 | 9.3 | 5.6 | 4.8 | 4.8 | 7 | 6 | 6 | 1461 | 924 | 924 | 2233 | 1458 | 1468 |
| RSL | KS | 10.3 | 8.9 | 8.9 | 5.6 | 4.7 | 4.7 | 7 | 6 | 6 | 1379 | 859 | 860 | 3057 | 1707 | 1748 |
| SDB | CA | 11.2 | 10.9 | 10.8 | 6.3 | 6.3 | 6.3 | 7 | 7 | 7 | 1900 | 1794 | 1784 | 4410 | 4752 | 4762 |
| AMA = Amarillo (TX) | CAO = Clayton (NM) |
|---|---|
| CDB = Cold Bay (AK) | CSM = Clinton (OK) |
| DDC = Dodge City (KS) | GCK = Garden City (KS) |
| GDP = Pine Springs (TX) | HBR = Hobart (OK) |
| RSL = Russell (KS) | SDB = Sandberg (CA) |
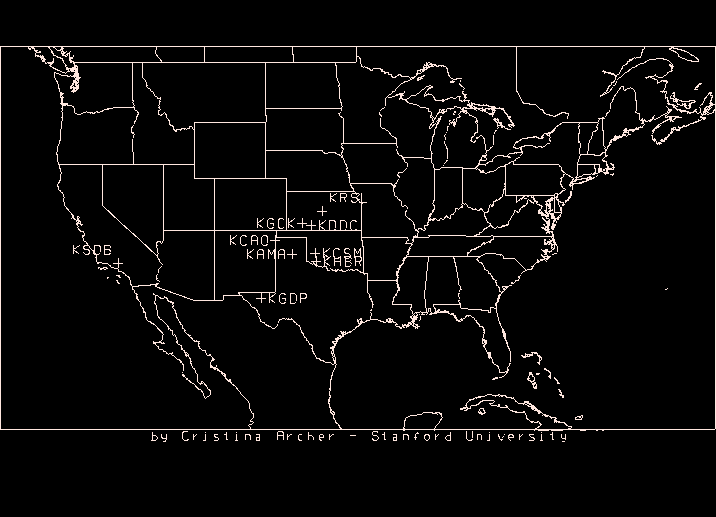 This map is available in Postscript format here
This map is available in Postscript format here
| AMA = Amarillo (TX) | CAO = Clayton (NM) |
|---|---|
| CDB = Cold Bay (AK) | CSM = Clinton (OK) |
| DDC = Dodge City (KS) | GCK = Garden City (KS) |
| GDP = Pine Springs (TX) | HBR = Hobart (OK) |
| RSL = Russell (KS) | SDB = Sandberg (CA) |
| AMA = Amarillo (TX) | CAO = Clayton (NM) |
|---|---|
| CDB = Cold Bay (AK) | CSM = Clinton (OK) |
| DDC = Dodge City (KS) | GCK = Garden City (KS) |
| GDP = Pine Springs (TX) | HBR = Hobart (OK) |
| RSL = Russell (KS) | SDB = Sandberg (CA) |
| AMA = Amarillo (TX) | CAO = Clayton (NM) |
|---|---|
| CDB = Cold Bay (AK) | CSM = Clinton (OK) |
| DDC = Dodge City (KS) | GCK = Garden City (KS) |
| GDP = Pine Springs (TX) | HBR = Hobart (OK) |
| RSL = Russell (KS) | SDB = Sandberg (CA) |
| AMA = Amarillo (TX) | CAO = Clayton (NM) |
|---|---|
| CDB = Cold Bay (AK) | CSM = Clinton (OK) |
| DDC = Dodge City (KS) | GCK = Garden City (KS) |
| GDP = Pine Springs (TX) | HBR = Hobart (OK) |
| RSL = Russell (KS) | SDB = Sandberg (CA) |