Recurrent back-propagation networks came into use shortly after the development of the back-propagation algorithm was first developed, and there are many variants of such networks. Williams and Zipser (1995) provide a thorough review of the recurrent back-propagation computational framework. Here we descibe a particular variant, used extensively in PDP models the effects of brain injury on lexical and semantic processing (Plaut and Shallice, 1993; Plaut et al., 1996; Rogers et al., 2004; Dilkina et al., 2008).
A major source of motivation for the use of recurrent backpropagation networks in this area is the intuition that they may provide a way of understanding the pattern of degraded performance seen in patients with neuropsychological deficits. Such patients make a range of very striking errors. For example, some patients with severe reading impairments make what are called semantic errors – misreading APRICOT as PEACH or DAFFODIL as TULIP. Other patients, when redrawing pictures they saw only a few minutes ago, will sometimes put two extra legs on a duck, or draw human-like ears on an elephant.
In explaining these kinds of errors, it has been tempting to think of the patient as having settled into the wrong basin of attraction in a semantic attractor network. For cases where the patient reads ‘PEACH’ instead of ‘APRICOT’, the idea is that there are two attractor states that are ‘near’ each other in a semantic space. A distortion, either of the state space itself, or of the mapping into that space, can result in an input that previously settled to one attractor state settling into the neighboring attractor. Interestingly, patients who make these sorts of semantic errors also make visual errors, such as misreading ‘cat’ as ‘cot’, or even what are called ‘visual-then-semantic’ errors, mis-reading ‘sympathy’ as ‘orchestra’. All three of these types of errors have been captured using PDP models that rely on the effects of damage in networks containing learned semantic attractors (Plaut and Shallice, 1993). Figure 8.1 from Plaut and Shallice (1993) illustrates how both semantic and visual errors can occur as a result of damage to an attractor network that has learned to map from orthography (a representation of the spelling of a word) to semantics (a represenation of the word’s meaning), taking printed words and mapping them to basins of attraction within a recurrent semantic network.
The use of networks with learned semantic attractors has an extensive history in work addressing semantic and lexical deficits, building from the work of Plaut and Shallice (1993) and other early work (Farah and McClelland, 1991; Lambon Ralph et al., 2001). Here we focus on a somewhat more recent model introduced to address a progressive neuropsychological condition known as semantic dementia by Rogers et al. (2004). In this model, the ‘semantic’ representation of an item is treated as an attractor state over an population of neurons thought to be located in a region known as the ‘temporal pole’ or anterior temporal lobe. The neurons in this integrative layer receive input from, and project back to, a number of different brain regions, each representing a different type of information about an item, including what it looks like, how it moves, what it sounds like, the sound of its name, the spelling of the word for it, etc. The architecture of the model is sketched in Figure 8.2 (top). Input coming to any one of the visible layers can be used to activate the remaining kinds of information, via the bi-directional connections among the visible layers and the integrative layer and the recurrent connections among the units in the integrative layer. According to the theory behind the model, progressive damage to the neurons in the integrative layer and/or to the connections coming into and out of this integrative layer underlies the progressive deterioration of semantic and abilities in semantic dementia patients (?).
In the version of recurrent back propagation that we consider here, activations of units are thought of as being updated continuously over some number of time intervals. The network is generally set to an initial state (corresponding to time 0), in which some units are clamped to specific values by external inputs, while others are initialized to a default starting value. Processing then proceeds in what is viewed conceptually as a continuous process for the specified number of time intervals. At any point along the way, target patterns can be provided for some of the pools of units in the network. Typically, these networks are trained to settle to a single final state, which is represented by a target to be matched over a subset of the pools in the network, over the last few time intervals.
At the end of the forward activation process, error signals are “back propagated through time” to calculate delta terms for all units in the network across the entire time span of the settling process. A feature of recurrent back-propagation is that the same pool of units can have both external inputs (usually provided over the first few time intervals) and targets (usually specified for the last few intervals). These networks are generally thought of as settling to attractor states, in which there is a pattern of activation over several different output pools. In this case, the target pattern for one of these pools might also be provided as the input. This captures the idea that I could access all aspects of my concept of, for example, a clock, either from seeing a clock, hearing a clock tick, hearing or reading the word clock, etc.
One application of these ideas is in the semantic network model of Rogers et al. (2004). A schematic replica of this model is shown in Figure 8.2 (top). There are three sets of visible units, corresponding to the name of the object, other verbal information about the object, and the visual appearance of the object. Whichever pattern is provided as the input, the task of the network is to settle to the complete pattern, specifying the name, the other verbal information about the object, and the visual percept. Thus the model performs pattern completion, much like, for example, the Jets-and-Sharks iac model from Chapter 2. A big difference is that the Rogers et al. (2004) model uses learned distributed representations rather than instance units for each known concept.
The actual computer simulation model, called rbp, treats time, as other networks do, as a sequence of discrete steps spanning some number of cannonical time intervals. The number of such intervals is represented by the variable nintervals. In rbp, the discrete time steps, called ticks, can slice the whole span of time very finely or very coursely, depending on the value of a parameter called dt. The number of ticks per interval is 1∕dt, and the total number of ticks of processing is equal to nintervals∕dt. The number of states of the network is one larger than the number of ticks; there is an initial state, at time 0, and a state at the end of each tick — so that the state at the end of tic 1 is state 1, etc.
To understand the recurrent backpropagation network, it is useful to visualize the states of all of the units in the network laid out on a series of planes, with one plane per state (Figure 8.2). Within each plane all of the pools of units in the network are represented. Projections are thought of as going forward from one plane to the next. Thus if pool(3) of a network receives a projection from pool(2), we can visualize nticks separate copies of this projection, one to the plane for state 1 from the plane for state 0, one to the plan for state 2 from the plan for state 2, etc.
Processing begins after the states of all of the units have been initialized to their starting values for state 0. Actually, both the activations of units, and their net inputs, must be initialized. The net inputs are set to values that correspond to the activation (by using the inverse logistic function to calculate the starting net input from the starting activation). For cases where the unit is clamped at 0 or 1, the starting net input is based on the correct inverse logistic value for 2.0e-8 and 1-(2.0e-8). [CHECK]
After the net inputs and activations have been established for state 0, the net inputs are calculated for state 1. The resulting net input value is essentially a running average, combining what we will call the newnet, based on the activations at the previous tick with the old value of the net input:
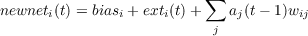
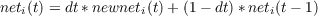
After net inputs for state t have been computed, activation values for state t are then computed based on each unit’s net input for state t. A variant on this procedure (not available in the rbp simulator) involves using the newnet to calculate a newact value, and then time averaging is then applied on the activations:
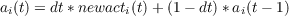
Time-averaging the net inputs is preferred because net input approximates a neuron’s potential while activation approximates its firing rate, and it is generally thought that it is the potential that is subject to time averaging (‘temporal summation’). Also, time-averaging the net input allows activation states to change quickly if the weights are large. The dynamics seems more damped when time-averaging is applied to the activations.
Once activation values have been computed, error measures and delta terms (called dEdnet) are calculated, if a target has been specified for the given state of the unit. The error is thought of as spread out over the ticks that make up each interval over which the target is applied, and so the magnitude of the error at each time step is scaled by the size of the time step. Either sum squared error (sse) or cross entropy error (cee) can be used as the error measure whose derivative drives learning. In either case, we compute both measures of error, since this is fast and easy. The sse for a given unit at a given time step is
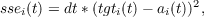
where tgti(t) is the externally supplied target at tick t. The cce for a given unit at a given time step is
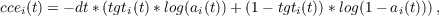
In the forward pass we also calculate a quantity we will here call the ‘direct’ dEdnet for each time step. This is that portion of the partial derivative of the error with respect to the net input of the unit that is directly determined by the presence of a target for the unit at time step t. If squared error is used, the direct dEdnet is given by
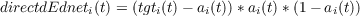
If cross-entropy error is used instead, we have the following simpler expression, due to the cancellation of part of the gradient of the activation function with part of the derivative of the cross entropy error:
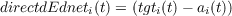
The overall error measure for a specific unit is summed over all ticks for which a target is specified:
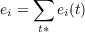
The activations of each unit in each tick are kept in an array called the activation history. Each pool of units keeps its own activation history array, which has dimensions [nticks+1, nunits]
We are now ready for the backward propagation of the dEdnet values. We can think of the dEdnet values as being time averaged in the backwards pass, just as the net inputs are in the forward pass. Each state propagates back to the preceding state, both through the time averaging and by back-propagation through the weights, from later states to earlier states:
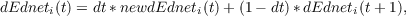
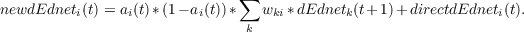
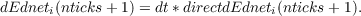
All of the dEdneti(t) values are maintained in an array called dEdnethistory. As with the activations, there is a separate dEdnet history for each pool of units, which like the activation history array, has dimensions [nticks+1,nunits]. (In practice, the values we are calling directdEdnet scaled by dt and placed in this history array on the forward pass, and the contents of that array is thus simply incremented during the backward pass).
After the forward pass and the backward pass, we are ready to calculate the weight error derivatives arising from this entire episode of processing in the network. This calculation is very simple. For each connection weight, we simply add together the weight error derivative associated with each processing tick. The weight error derivative for each tick is just the product of the activation of the sending unit from the time step on the input side of the tick times the dEdnet value of the receiving unit on the receiving side of the tick:
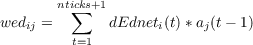
Once we have the weight error derivatives, we proceed exactly as we do in the back propagation algorithm as implemented in the bp program. As in standard back propagation, we can update the weights once per pattern, or once per N patterns, or once per epoch. Patterns may be presented in sequential, or permuted order, again as in the bp program. Momentum and weight decay can also be applied.
Training and testing in rbp work much the same as in other networks. The rogers network has been set up in advance for you, and so you can launch the program to run the rogers example by simply typing rogers at the MATLAB commmand prompt while in the rbp directory. See Figure 8.3 for the screen layout of this network.
During testing, the display can be updated (and the state of the network can be logged) at several different granularities: At the tick level, the interval level, and the pattern level. When tick level or interval level is specified, state 0 is shown first, followed by the state at the end of the first tick or interval, until the end of the final tick is reached. The template for the rogers model, rogers.m, also displays the target (if any) associated with the state, below the activations of each pool of units in the network. With updating at the pattern level, the state is updated only once at the end of processing each pattern.
Back propagation of error occurs only during training, although during training the display update options are limited to the pattern and the epoch level. The user can log activations forward and deltas back at the tick level via the set write options button in the train options panel (select backtick for ‘frequency’ of logging). Otherwise logging only occurs in the forward direction.
A great deal of computing is required to process each pattern, and thus it takes quite a long time to run one epoch in the rbp program. To ameliorate this problem, we have implemented the pattern processing steps (forward pass, backward pass, and computing the weight error derivatives) within a ‘mex’ file (essentially, efficient C code that iterfaces with Matlab data formats and structures).Fast mode is approximately 20 times faster than the regular mode. To turn on the fast mode for network training, click the ’fast’ option in the train window. This option can also be set by typing the following command on the MATLAB command prompt:
runprocess(’process’,’train’,’granularity’,’epoch’,’count’,1,’fastrun’,1);
There are some limitations in executing fast mode of training.In this mode, network output logs can only be written at epoch level. Any smaller output frequency if specified, will be ignored.When running with fast code in gui mode, network viewer will only be updated at epoch level.Smaller granularity of display update is disabled to speed up processing.
There is a known issue with running this on linux OS.MATLAB processes running fast version appear to be consuming a lot of system memory. This memory management issue has not been observed on windows. We are currently investigating this and will be updating the documentation as soon as we find a fix.
As provided the training pattern file used with the rogers network, (features.pat) contains 144 patterns. There are 48 different objects (eight each from six categories), with three training patterns for each. One provides external input to the name units, one to the verbal descriptor units (one large pool consisting of ‘perceptual’, ‘functional’ and ‘encyclopedic’ descriptors) and one provides input to the visual features units. In all three cases, targets are specified for all three visible pools. Each of the three visible pools is therefore an ‘inout’ pool. The network is set up to use Cross-Entropy error. If cross entropy error is not used, the network tends to fail to learn to activate all output units correctly. With cross-entropy error, this problem is avoided, and learning is quite robust.
If one wanted to simulate effects of damage to connections in the rogers network, the best approach would be to apply a mask to the weights in particular projections. For example, to lesion (i.e. zero out) weights in net.pool(4).proj(3) with r receivers and s senders, with a lesion probability of x:
This creates a mask matrix with each entry being zero with probability x and 1 with probability 1 - x.
This will zero out all of the weights associated with mask values of 0. You can apply further lesions if you wish or re-load and apply different lesions as desired.
One can add Gaussian noise with standard deviation s to the weights in a particular projection even more simply:
Lesioning units is a bit more complicated, and routines need to be implemented to accomplish this.
The pattern file must begin with the string ‘rbp’ and this is followed by a ‘:’ and two numbers, nintervals and ticks per interval. In the example provided (features.pat, for use with the rogers network) this line is thus:
The pattern specifications follow the single header line. Here is an example of a pattern specification from the rogers network:
Each pattern specification begins with a pname followed by one or more input specifications and one or more target specifications followed by end. Input specifications begin with the letter H or S to indicate whether the pattern should be hard or soft clamped, followed by a start time and a duration. The first interval is interval 1 so to clamp from the beginning of a pattern presentation and leave the input clamped for three intervals, you would have 1 3. This information is followed by the name of the layer to which the pattern should be applied, followed by a string of numbers specifying input values for each unit in the pool. If the letter is H the states of the units in the specified pool are hard clamped to the input values. If the letter is S the value specified is treated as a component of the net input of the unit. In this case the input value and the unit’s bias determine its initial net input for state 0, and its activation is set to the appropriate value for that net input.
For both hard and soft clamps, the input is applied to the state at the starting edge of the start time indicated, and remains in place for duration*ticksperinterval. In this case, the values 1 3 mean that the input is clamped on in states 0 through 11. This does not include the state at the starting edge of interval 4 (state 12).
Target specifications begin with the letter T then a start time and a duration. In this case the values are 6 and 2, specifying that the target is clamped for two intervals beginning with interval 6. The target applies to the state at the trailing edge of the first tick after the start time. So in this case the target applies to states 22 to 29. As with input patterns, the start time and duration are followed by a pool name and a sequence of values specifying targets for the units in the pool indicated.
When creating an rbp network, it is necessary to specify the value of the variables net.nintervals and net.ticksperinterval.The values of these variables should be specified immediately after specifying the network type as an rbp network, before specifying pools and projections. Once created the .net file can be edited to change these parameters if desired, but the program must be closed and restarted for these changes to take effect. This makes it possible to train the network for some number of epochs with ticksperinteral at 1 and then save the weights, exit the program, change ticks per interval to 5, and then restart the network and reload the weights for fine tuning.
Specifying pools and projections in rbp is similar to other programs. Note however that in rbp, layers can project to themselves and there can be both a projection from layer a to layer b and from layer b to layer a. All these projections are options, and each must be independently specified in the network specification file. Note also that layers can be input, output, inout, or hidden layers. An inout layer can have external inputs specified and also have targets specified.