Contents
Generate problem data
randn('seed', 0);
rand('seed', 0);
n = 100;
N = 10*n;
Sinv = diag(abs(ones(n,1)));
idx = randsample(n^2, 0.001*n^2);
Sinv(idx) = ones(numel(idx), 1);
Sinv = Sinv + Sinv';
if min(eig(Sinv)) < 0
Sinv = Sinv + 1.1*abs(min(eig(Sinv)))*eye(n);
end
S = inv(Sinv);
D = mvnrnd(zeros(1,n), S, N);
Solve problem
[X, history] = covsel(D, 0.01, 1, 1);
iter r norm eps pri s norm eps dual objective
1 0.5604 0.0878 7.6521 0.0156 66.74
2 0.2677 0.1230 3.6651 0.0176 47.97
3 0.0890 0.1453 2.2727 0.0181 41.51
4 0.0341 0.1608 1.5731 0.0182 38.54
5 0.0223 0.1720 1.1563 0.0183 36.98
6 0.0193 0.1806 0.8831 0.0183 36.08
7 0.0168 0.1872 0.6927 0.0183 35.54
8 0.0147 0.1924 0.5544 0.0183 35.19
9 0.0126 0.1967 0.4507 0.0183 34.97
10 0.0110 0.2001 0.3710 0.0183 34.82
11 0.0092 0.2029 0.3087 0.0183 34.71
12 0.0079 0.2053 0.2592 0.0183 34.64
13 0.0074 0.2072 0.2192 0.0183 34.59
14 0.0060 0.2088 0.1867 0.0183 34.55
15 0.0051 0.2102 0.1600 0.0183 34.52
16 0.0044 0.2114 0.1378 0.0183 34.50
17 0.0036 0.2124 0.1192 0.0183 34.48
18 0.0031 0.2132 0.1036 0.0183 34.47
19 0.0028 0.2140 0.0904 0.0183 34.46
20 0.0025 0.2146 0.0792 0.0182 34.46
21 0.0023 0.2151 0.0696 0.0182 34.45
22 0.0019 0.2156 0.0613 0.0182 34.45
23 0.0016 0.2160 0.0542 0.0182 34.44
24 0.0014 0.2163 0.0480 0.0182 34.44
25 0.0013 0.2166 0.0426 0.0182 34.44
26 0.0011 0.2169 0.0379 0.0182 34.44
27 0.0012 0.2171 0.0337 0.0182 34.44
28 0.0040 0.2173 0.0299 0.0182 34.44
29 0.0021 0.2175 0.0265 0.0182 34.44
30 0.0013 0.2177 0.0236 0.0182 34.43
31 0.0009 0.2178 0.0211 0.0182 34.43
32 0.0008 0.2179 0.0188 0.0182 34.43
33 0.0007 0.2181 0.0169 0.0182 34.43
Elapsed time is 0.388161 seconds.
Reporting
K = length(history.objval);
X_admm = X;
h = figure;
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');
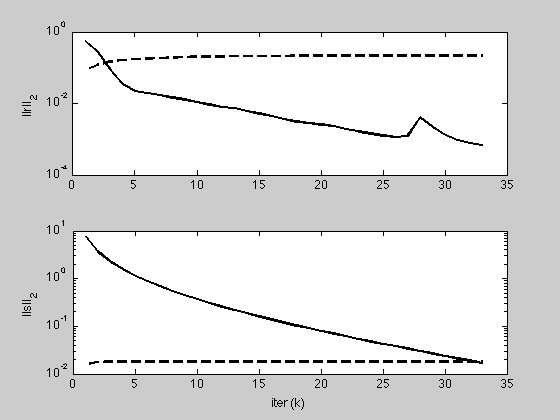
g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
1:K, history.eps_pri, 'k--', 'LineWidth', 2);
ylabel('||r||_2');
subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');