group_lasso_feat_split

Generate problem data
Solve problem
Reporting

% Group lasso example with random data

Generate problem data

randn('seed', 0);
rand('seed',0);

m = 200;        % amount of data
K = 200;        % number of blocks
ni = 100;       % size of each block

n = ni*K;
p = 10/K;      % sparsity density

% generate block sparse solution vector
x = zeros(ni,K);
for i = 1:K,
    if( rand() < p)
        % fill nonzeros
        x(:,i) = randn(ni,1);
    end
end
x = vec(x);

% generate random data matrix
A = randn(m,n);

% normalize columns of A
A = A*spdiags(1./norms(A)',0,n,n);

% generate measurement b with noise
b = A*x + sqrt(1)*randn(m,1);

% lambda max
for i = 1:K,
    Ai = A(:,(i-1)*ni + 1:i*ni);
    nrmAitb(i) = norm(Ai'*b);
end
lambda_max = max( nrmAitb );

% regularization parameter
lambda = 0.5*lambda_max;

xtrue = x;   % save solution

Solve problem

[x history] = group_lasso_feat_split(A, b, lambda, ni, 10, 1.0);

iter	    r norm	   eps pri	    s norm	  eps dual	 objective
  1	    2.3930	    0.0381	   17.0674	    0.1848	      1.43
  2	    2.2790	    0.0369	    0.8127	    0.3474	      5.46
  3	    2.1705	    0.0358	    0.7740	    0.5022	     11.71
  4	    2.0671	    0.0348	    0.7372	    0.6496	     19.85
  5	    1.9687	    0.0338	    0.7021	    0.7900	     29.58
  6	    1.8750	    0.0329	    0.6686	    0.9237	     40.66
  7	    1.7857	    0.0320	    0.6368	    1.0511	     52.85
  8	    1.7006	    0.0311	    0.6065	    1.1724	     65.93
  9	    1.6197	    0.0303	    0.5776	    1.2879	     79.74
 10	    1.5425	    0.0296	    0.5501	    1.3979	     94.11
 11	    1.4691	    0.0288	    0.5239	    1.5027	    108.90
 12	    1.3991	    0.0281	    0.4989	    1.6025	    123.99
 13	    1.3325	    0.0275	    0.4752	    1.6975	    139.27
 14	    1.2690	    0.0268	    0.4526	    1.7881	    154.65
 15	    1.2035	    0.0262	    0.9770	    1.8739	    171.34
 16	    1.1235	    0.0259	    2.5228	    1.9540	    192.49
 17	    1.0104	    0.0265	    4.5664	    2.0259	    223.10
 18	    0.8238	    0.0291	    6.9308	    2.0844	    274.81
 19	    0.5626	    0.0340	    9.0543	    2.1237	    348.80
 20	    0.2850	    0.0405	   10.1061	    2.1416	    431.85
 21	    0.1532	    0.0475	    9.9143	    2.1399	    507.79
 22	    0.2843	    0.0544	    8.7940	    2.1232	    565.18
 23	    0.3983	    0.0598	    7.2726	    2.0975	    599.60
 24	    0.4429	    0.0637	    5.9129	    2.0685	    611.80
 25	    0.4316	    0.0663	    5.0450	    2.0403	    607.52
 26	    0.3822	    0.0679	    4.7318	    2.0159	    591.95
 27	    0.3126	    0.0688	    4.8115	    1.9970	    569.94
 28	    0.2398	    0.0694	    4.8365	    1.9843	    545.46
 29	    0.1871	    0.0699	    4.3953	    1.9766	    525.24
 30	    0.1564	    0.0705	    3.8550	    1.9726	    510.50
 31	    0.1410	    0.0711	    3.3495	    1.9713	    499.88
 32	    0.1345	    0.0718	    3.0667	    1.9720	    492.32
 33	    0.1326	    0.0726	    2.8673	    1.9740	    486.53
 34	    0.1318	    0.0734	    2.6498	    1.9770	    482.70
 35	    0.1298	    0.0744	    2.4048	    1.9804	    481.15
 36	    0.1257	    0.0754	    2.1827	    1.9837	    481.60
 37	    0.1205	    0.0765	    2.0746	    1.9865	    483.14
 38	    0.1155	    0.0776	    2.0266	    1.9889	    484.94
 39	    0.1105	    0.0787	    1.9408	    1.9907	    487.21
 40	    0.1060	    0.0797	    1.8610	    1.9918	    489.74
 41	    0.1023	    0.0808	    1.8082	    1.9923	    492.15
 42	    0.0994	    0.0818	    1.7469	    1.9922	    494.27
 43	    0.0971	    0.0828	    1.6476	    1.9916	    496.33
 44	    0.0952	    0.0837	    1.5846	    1.9906	    497.96
 45	    0.0932	    0.0846	    1.5221	    1.9893	    499.13
 46	    0.0911	    0.0853	    1.4628	    1.9878	    499.86
 47	    0.0887	    0.0860	    1.3806	    1.9862	    500.33
 48	    0.0861	    0.0867	    1.3136	    1.9845	    500.65
Elapsed time is 7.236219 seconds.

Reporting

K = length(history.objval);

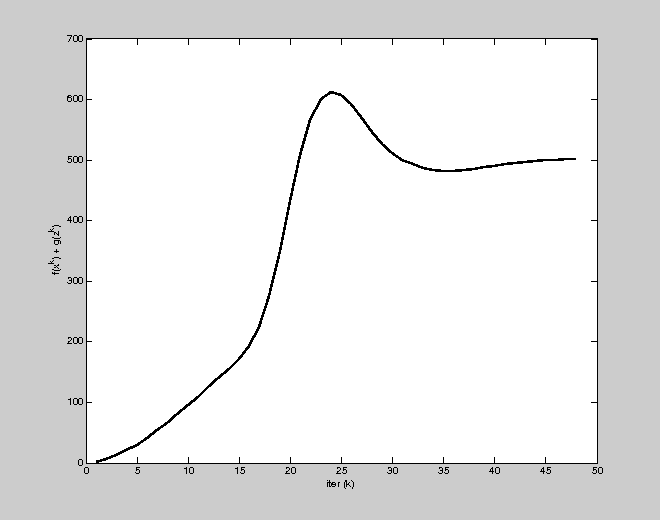
h = figure;
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');

g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
    1:K, history.eps_pri, 'k--',  'LineWidth', 2);
ylabel('||r||_2');

subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
    1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');

Contents

Generate problem data

Solve problem

Reporting