Contents
Generate problem data
randn('seed', 0);
rand('seed',0);
m = 1500;
n = 5000;
p = 100/n;
x0 = sprandn(n,1,p);
A = randn(m,n);
A = A*spdiags(1./sqrt(sum(A.^2))',0,n,n);
b = A*x0 + sqrt(0.001)*randn(m,1);
lambda_max = norm( A'*b, 'inf' );
lambda = 0.1*lambda_max;
Solve problem
[x history] = lasso(A, b, lambda, 1.0, 1.0);
iter r norm eps pri s norm eps dual objective
1 3.7048 0.0465 0.7250 0.0441 3.35
2 2.2654 0.0409 1.7960 0.0653 10.13
3 1.0958 0.0529 2.0325 0.0734 15.14
4 0.8050 0.0687 1.7219 0.0736 17.68
5 0.8619 0.0801 1.2234 0.0704 18.69
6 0.8078 0.0864 0.7669 0.0667 18.92
7 0.6611 0.0889 0.4398 0.0635 18.80
8 0.4906 0.0890 0.2659 0.0612 18.49
9 0.3379 0.0878 0.2159 0.0598 18.12
10 0.2255 0.0861 0.1987 0.0591 17.78
11 0.1585 0.0845 0.1721 0.0590 17.51
12 0.1212 0.0833 0.1379 0.0591 17.35
13 0.0979 0.0825 0.1044 0.0595 17.27
14 0.0799 0.0820 0.0759 0.0598 17.25
15 0.0650 0.0819 0.0532 0.0602 17.27
Elapsed time is 1.803560 seconds.
Reporting
K = length(history.objval);
h = figure;
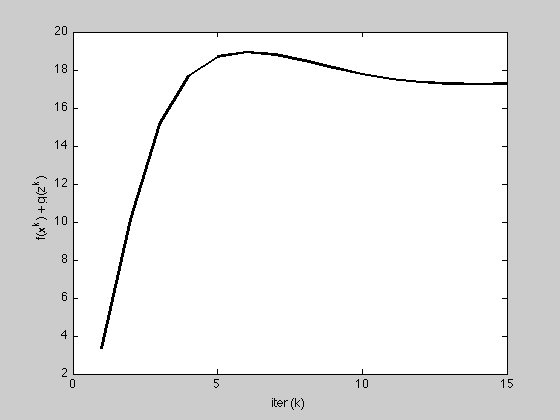
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');
g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
1:K, history.eps_pri, 'k--', 'LineWidth', 2);
ylabel('||r||_2');
subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');