Contents

% Cardinality constrained least-squares example (nonconvex)

Generate problem data

randn('seed', 0);
rand('seed',0);

m = 1500;       % number of examples
n = 5000;       % number of features
p = 100/n;      % sparsity density

% generate sparse solution vector
x = sprandn(n,1,p);

% generate random data matrix
A = randn(m,n);

% normalize columns of A
A = A*spdiags(1./sqrt(sum(A.^2))', 0, n, n);

% generate measurement b with noise
b = A*x + sqrt(0.001)*randn(m,1);

xtrue = x;   % save solution

Solve problem

[x history] = regressor_sel(A, b, p*n, 1.0);

iter	    r norm	   eps pri	    s norm	  eps dual	 objective
  1	    3.1818	    0.0465	    2.3330	    0.0389	      5.38
  2	    1.1927	    0.0585	    2.6814	    0.0487	      7.92
  3	    1.1216	    0.0790	    2.2545	    0.0485	      6.72
  4	    1.2543	    0.0934	    1.7125	    0.0446	      4.94
  5	    1.3137	    0.1020	    1.4387	    0.0400	      3.57
  6	    1.2244	    0.1070	    1.1351	    0.0349	      2.49
  7	    1.0563	    0.1093	    0.8049	    0.0304	      1.77
  8	    0.8269	    0.1095	    0.4945	    0.0276	      1.40
  9	    0.5639	    0.1085	    0.2625	    0.0265	      1.29
 10	    0.3841	    0.1069	    0.2960	    0.0263	      1.28
 11	    0.3259	    0.1054	    0.3102	    0.0264	      1.28
 12	    0.2956	    0.1041	    0.2813	    0.0263	      1.26
 13	    0.3156	    0.1032	    0.2956	    0.0263	      1.25
 14	    0.2677	    0.1027	    0.1912	    0.0263	      1.23
 15	    0.2134	    0.1025	    0.1609	    0.0263	      1.24
 16	    0.1605	    0.1025	    0.0817	    0.0264	      1.24
 17	    0.1059	    0.1025	    0.0578	    0.0266	      1.25
 18	    0.1503	    0.1025	    0.1397	    0.0267	      1.26
 19	    0.1164	    0.1026	    0.0708	    0.0268	      1.27
 20	    0.0712	    0.1026	    0.0459	    0.0269	      1.28
 21	    0.0557	    0.1026	    0.0319	    0.0270	      1.29
 22	    0.0425	    0.1026	    0.0253	    0.0271	      1.30
Elapsed time is 2.188126 seconds.

Reporting

K = length(history.objval);

h = figure;
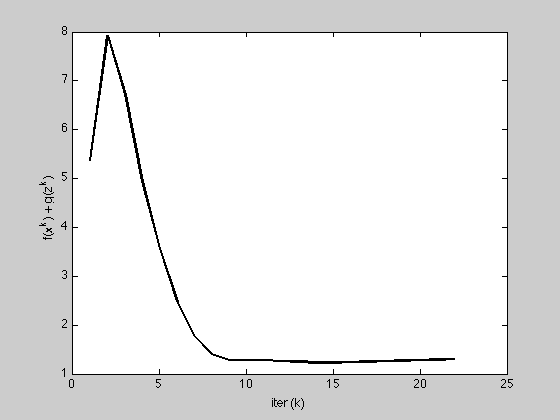
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');

g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
    1:K, history.eps_pri, 'k--',  'LineWidth', 2);
ylabel('||r||_2');

subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
    1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');

Compare to l1 regularization

% err1 = [];
% card1 = [];
% for K = 1:5:2*p*n
%     [x history] = regressor_sel(A, b, K, rho);
%     err1 = [err1 norm(A*x - b)];
%     card1 = [card1 K];
% end
%
% % lambda max
% lambda_max = norm( A'*b, 'inf' );
%
% err2 = [];
% card2 = [];
% for lambda = (1:-.01:.02)*lambda_max
%     [x history] = lasso(A, b, lambda, rho, 1);
%     err2 = [err2 norm(A*x - b)];
%     card2 = [card2 sum(x~=0)];
% end
%
% p = figure
% stairs(card1, err1, 'k', 'LineWidth', 2);
% hold on;
% stairs(card2, err2, 'k--', 'LineWidth', 2);
% ylabel('||Ax-b||'); xlabel('card(x)');
% legend('regressor selection', 'l1 regularization');


Published with MATLAB® 7.7