A General Framework for Dynamic Time Warping
Optimization and Engineering, 2022.
The goal of dynamic time warping is to transform or warp time in order to
approximately align one signal with another. We pose the choice of warping
function as an optimization problem with several terms in the objective. The
first term measures the misalignment of the time-warped signal and its target.
Two additional regularization terms penalize the cumulative warping and the
instantaneous rate of time warping; constraints on the warping can be imposed
by assigning the value 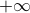 to the regularization terms.
Different choices of the
three objective terms yield different time warping functions that trade off
signal fit or alignment and properties of the warping function. The
optimization problem we formulate is a classical optimal control problem, with
initial and terminal constraints, and a state dimension of one. We describe an
effective general method that minimizes the objective by discretizing the
values of the original and warped time, and using standard dynamic programming
to compute the (globally) optimal warping function with the discretized values.
Iterated refinement of this scheme yields a high accuracy warping function in
just a few iterations. Our method is implemented as an open source Python
package gdtw.
to the regularization terms.
Different choices of the
three objective terms yield different time warping functions that trade off
signal fit or alignment and properties of the warping function. The
optimization problem we formulate is a classical optimal control problem, with
initial and terminal constraints, and a state dimension of one. We describe an
effective general method that minimizes the objective by discretizing the
values of the original and warped time, and using standard dynamic programming
to compute the (globally) optimal warping function with the discretized values.
Iterated refinement of this scheme yields a high accuracy warping function in
just a few iterations. Our method is implemented as an open source Python
package gdtw.