Polyphase Motor/Generator Page
The Polyphase Motor/Generator
There's no such thing as free energy...turn your own crank!
![[hand crank]](./thumb/pmg/pmgcrank_18-t.jpg)
(Click on thumbnails to view larger images.)
Please check the licensing link below for use and licensing information
for the contents of this web site. Thanks!
licensing
![[Rainforest Site]](./gifs/rainforest.gif)
Click here for my boundary layer turbine page.
![[new]](./gifs/new.gif) Click here for my mark-II boundary layer turbine page.
Click here for my mark-II boundary layer turbine page.
Click here for my single-phase motor/generator page.
Click here for my solar powered fluid mechanics lab page.
Click here for my 3-axis CNC machine page.
Click here for my $662.00 supercomputer page.
![[new]](./gifs/new.gif) Click here for my miscellaneaganza! page.
Click here for my miscellaneaganza! page.
![[best use any browser]](./gifs/vbrowser.gif)
![[under construction]](./gifs/constr.gif)
Home
Contents:
The Real Story:
OK, I've wanted to build a hand cranked generator and use it to bright up a
light bulb ever since I was in the fourth grade. Now, pushing 40 years later,
I'm fiddling with this Tesla Turbine project, and I finally have a good excuse
to figure out how to do it. That being I want something to drive with upcoming
versions of the turbine in order to do some simple power capacity tests, and
also something to use while figuring out fuzzy logic control circuits for
hybrid vehicle battery charging systems.
In keeping with the trend in modern electric and hybrid/electric vehicle
technology, the motor/generator to be discussed in this report is a polyphase
brushless permanent magnet design. Polyphase brushless permanent magnet motors
are becoming more popular for use in modern electric and hybrid/electric
vehicles than the magnetless and single-phase varieties because they are easier
to start, easier to control, easier to drive, and tend to have greater power
densities. They also make a perfectly fine generator, so they can be used for
regenerative breaking and battery charging in an electric vehicle, as well as
for the drive motor.
Three-phase is the most commonly found polyphase system, and, the model
motor/generator presented below is a 3-phase unit. (By the way, Nikola Tesla is
much more famous for his invention of polyphase motor/generators, and AC power
generation and distribution than he is for his invention of the boundary layer
turbine.) The motor/generator described here is also a "pancake" design, having
a flat disc rotor with magnets on the disc face, rather than spaced around the
rotor circumference. And, similarly, it has a flat armature, with coils mounted
to face the rotor magnets. While permanent magnet brushless motors can in
general be made smaller than other styles of motor for the same power
capability, the pancake style motor can provide even greater space savings over
more conventional cylindrical motor designs.
The entire model three-phase brushless motor generator construction project is
documented in this report. That documentation includes the making of a winder
for the armature coils, and the collection of magnetite (eventually not) used
to fill the armature coil center holes. Dimensioned drawings for the basic
units of the motor/generator are also provided.
The theory of operation for three-phase motor/generators in general, and the
brushless permanent magnet variety in particular, are provided in the final
section of this report. The theory of operation for 3-phase brushless motor
driver circuits is presented there as well. Schematics for circuits used in the
model motor/generator design covered in this report are also included in the
final section.
Coil Winder:
If you're going to build a generator or a motor, then you're going to need some
coils. Even with permanent magnet rotors as used here, you'll still need
armature windings. Its pretty hard to get out much power otherwise. Some kind
of winder will make the task of producing consistent coils much easier. The
photos below show a simple coil winder, which includes a tally counter for
keeping track of the number of windings, and a threaded crank shaft that allows
attachment of arbitrarily shaped coil forms.
Besides 2"x2" wood stock, the winder is constructed mainly using 3/16" threaded
brass rod, 3/16" smooth brass rod, thin wall brass tubing, assorted pieces of
0.08" polystyrene sheet, a piece of aluminum window frame (cut to form the cam
which moves the tally counter push rod), some thin aluminum strips to hold the
tally counter in place, a piece of 3/4" PVC pipe to hold the wire spool, and
some wood screws.
The push rod hole and the crank shaft hole are sleeved with thin wall brass
tubing. The portion of the threaded rod which passes through the crank shaft
hole is itself sleeved with brass tubing, so it is tubing to tubing, not tubing
to thread contact on the turning parts. The holes in the cam piece are threaded
so it is effectively double nutted in place by the nuts which hold the cam to
the shaft. The winding handle has a free turning piece of brass rod over a
piece of threaded rod for easy cranking. There is a cotter pin through the
brass rod which pushes the tally counter lever. This cotter pin backs up
against a flat washer when the tally counter lever rebounds after being
pressed, and prevents the spring loading of the tally counter lever from
popping the push rod through its sleeve and into your lap while you are
winding coils. A nail can be slipped into a snug fit hole in the wooden frame
to hold the crank at its zero start position while the counter is reset and the
coil form is threaded.
The coil form shown is for simple round coils. It consists of a piece of
polystyrene tube, two washers cut from 0.08" polystyrene sheet, and two metal
washers. The length of the polystyrene tube is the desired thickness of the
coils to be wound (0.25" in this case), the OD of the tube is the desired ID
for the coils to be wound (0.375" in this case), and the OD of the polystyrene
washers is the desired OD for the coils to be wound (1.125" in this case).
The metal washers backup the polystyrene washers to prevent them from spreading
as the coil is wound. One of the polystyrene washers has a slot cut in it to
allow threading of the magnet wire used to wind the coil. That same washer has
a groove filed in it which extends from the inner end of the wire slot to the
outer edge of the washer. The groove allows the wire to be threaded under the
metal washer without crushing the wire then the wingnuts which hold the coil
form on the shaft are tightened. That's 24 AWG wire, in case you're wondering.
![[coil winder]](./thumb/pmg/coil_winder_1-t.jpg)
![[coil winder]](./thumb/pmg/coil_winder_2-t.jpg)
![[coil winder]](./thumb/pmg/coil_winder_3-t.jpg)
![[coil winder]](./thumb/pmg/coil_winder_4-t.jpg)
Magnetite Mining:
It can be a good idea to make armature coils which have their center holes
filled with a metal core. But, it can be a bad idea to use a solid chunk of
metal for this purpose. The reason for this (the reason why most transformers
are built with laminated rather than solid metal cores) is covered briefly in
the "How's it work?" section at the end of this report.
On one of the myriad do-it-yourself alternative power websites
[1] someone pointed out that a paste
of magnetite, (a common mineral of naturally occurring iron and iron oxides,
most often found as small sand sized particles), and polyester resin, could be
a good substitute for trying to make laminated sheet metal coil cores. They
obtained their magnetite by dragging a magnet around on their driveway. I
tried that, and it worked, but wasn't very satisfying, so I picked up my pail
and spade and headed to the beach to play in the sand.
Pouring sand over a salvage magnet found the stuff just fine. The magnetite
grains cling to the magnet, and the nonferromagnetic material just passes on
by. The salvage magnet I used consists of two steel plates sandwiching a plate
magnet, with that assembly surrounded by a square, U-shaped piece of heavy
sheet metal. There is about a 3/8" square gap between the base of the sheet
metal "U" and the magnet sandwiched between the steel plates. You can see
magnetite collecting on the edges of the steel plates in the photos below, but
the greater collection point was in the gap at the base of the sheet metal U.
After pouring sand over the magnet for a while, the magnetite collected in the
gap could be worried out with a small stick.
The first pour collection material contains a lot of low quality magnetite.
Once a couple of hand fulls of this material was gathered, it was refined by
passing a small, but very powerful neodymium magnet an inch or so
over the pile, and subcollecting the material that jumped to the small magnet.
The pile was stirred repeatedly, and small magnet passed over the stirred
material until no more magnetite jumped to the magnet. This refining process
was performed on the subcollected material, and again though several
iterations of subcollections. The result was a very pure collection of
magnetite.
![[magnetite]](./thumb/pmg/magnetite_3-t.jpg)
![[magnetite]](./thumb/pmg/magnetite_2-t.jpg)
![[magnetite]](./thumb/pmg/magnetite_1-t.jpg)
During the two hours or so it took to collect and refine an amount of
relatively pure magnetite sufficient for this motor/generator project, I had a
tiny epiphany..."Hey, this stuff looks just like the leavings that come out of
a break drum lathe!"... Break drums and rotors are cast iron, so, in fact, the
leavings should work much like magnetite. Having ready access to a such a
lathe, I went back to the shop and took another 45 seconds to gather a couple
of quarts of leavings. This material is what I eventually used to fill my
armature coil core holes.
![[cast iron]](./thumb/pmg/cast_iron_2-t.jpg)
![[cast iron]](./thumb/pmg/cast_iron_1-t.jpg)
Model 3-Phase Motor/Generator Construction:
Armature:
Besides having armature coils filled with a metal core, (as mentioned in the
Magnetite Mining section), it is also a good idea to have what is sometimes
referred to as "backing iron" behind the coils. As with filling the coil cores,
this metal should be disconnected laminations. On yet another of the myriad
do-it-yourself home energy websites [2]
someone mentioned that coat hanger wire (which generally has some form of
lacquer or plastic coating) could work well for filling coil cores. And, there
is no reason why that can't work for backing iron, too. You just have to cut a
shallow groove in the armature frame piece, (here I used 3/8" plywood, and
spun it on a lathe), making the groove wider than the width of the coils, lay
in pieces of coat hanger wire, and fill the groove with polyester resin to seal
everything in. The coils can then simply be glued in place over the sealed in
coat hanger wire pieces with more polyester resin.
This does work OK. But, don't try to use the springyness of the coat hanger
wire to hold things tightly in place. The fourth or fifth time it all jumps out
on the ground for you, you'll get the idea. Just bend the pieces to sit in
place on their own. And, if you don't have a wire bending jig, don't get too
fussy about the fit, unless you want to take a real, real, real long time.
(Hey, we're not building a watch here.)
I think if I do it again I'll use the coated metal banding used to strap heavy
items on to pallets for shipping. It's about 0.015 inches thick, and you can
get it in 100 foot lengths on a roll-off dispenser from industrial supply
houses (like McMaster-Carr) for relatively cheap (around $35.00). Cutting the
strapping material into pieces a few feet long, coiling them into the groove in
the armature frame piece and sealing them in with polyester resin should work
reasonably well. I may also investigate using the same magnetite/resin paste
used to fill the coil cores for backing iron.
A hole was drilled in the center of the backing iron groove circle for the axle
to pass through. The backing iron groove was turned in high enough up the
armature frame piece to allow clearance for the rotor to spin freely on its
axle when the entire motor/generator unit is assembled on its base.
![[armature]](./thumb/pmg/armature_1-t.jpg)
![[armature]](./thumb/pmg/armature_2-t.jpg)
![[armature]](./thumb/pmg/armature_3-t.jpg)
Rotor:
Construction of the 6" diameter rotor was very similar to construction of the
armature support piece. As for the armature coils, it is also a good idea to
have backing iron in a groove behind the magnets. But, with permanent magnets,
the need for laminations in the backing iron is much less than for coils, and a
plate of metal will do. I just cut a ring of about 18 gauge steel from an old
chunk of ventilation duct for this. The magnets stick to the metal plate, and
are spaced around the face of the rotor (alternating north and south poles up)
by inserting them into holes drilled into a ring of 0.08" polystyrene plastic
sheet material cut to fit in the groove above the backing iron ring.
The magnets used here are fairly powerful 3/4" diameter by 1/4" thick ferrite
types. Without the plastic spacer it would be very difficult to set the magnets
in place, unless you glue them individually, holding each one and waiting for
the glue to dry before setting the next one (quick set super glue would be a
plus there). The spacing of the magnets in the exploded view rotor assembly
photo below isn't just for aesthetics. That is about as close as you can place
them together without a sudden catastrophe.
The backing iron disc, polystyrene retainer disc, and the magnets are held in
place with hot melt glue. Since the forces trying to tear them out when the
rotor is spinning are all radial, and all the components are retained in the
groove in the 3/8" plywood rotor disc, they really don't require more than that
to hold them in place.
It would be desirable to use neodymium magnets for the rotor. Neodymium magnets
much more powerful and also much thinner than the ferrites used here are
available for less than $2.00 apiece (check on e-bay). Using those it would be
possible to smear a layer of polyester resin over the whole assembly to hold
the rotor components in place. Then there would be no danger of the assembly
coming apart while spinning. (I'll probably make that change someday.)
![[rotor]](./thumb/pmg/rotor_1-t.jpg)
![[rotor]](./thumb/pmg/rotor_3-t.jpg)
Balancing the rotor was accomplished through spinning it by hand on its axle
and bearing assembly and looking for the heavy spots. One piece of adhesive
backed lead (available from hobby shops for balancing model cars and airplanes)
needed to be cut and placed on the back side of the disc, opposite the position
that always ended up down when the rotation stopped. This resulted in quite
good balance of the rotor. Besides using its own adhesive, the lead piece was
glued in place with a glob of five-minute epoxy, and a glob of five-minute
epoxy the same volume as used for the lead piece was placed on the opposite
edge of the disc from the lead piece to ensure the balance wasn't changed by
the glue. (In the picture showing the lead balance piece, the bit of stuff
visible in the shaft hole in the hub is the rolled back edge of a piece of thin
brass shim material.)
![[rotor]](./thumb/pmg/balance_1-t.jpg)
Axle:
The axle itself is a piece of 1/4" diameter cold rolled steel rod. A hub to
hold the rotor was made by cutting a 1-11/16" diameter disc from 3/16" steel,
center drilling it for the axle shaft to slide through, and drilling 4 holes
around the edge of the disc, tapping them for 1/4"-20 screws. (These holes
accept the screws used to attach the rotor disc to the hub.) A piece of 5/8"
diameter rod 2" long was bored to accept the 1/4" shaft rod and also drilled
and tapped for two 1/4"-20 screws to clamp the hub to the axle shaft. The 2"
long drilled rod was then welded in place over the center hole in the 1-11/16"
diameter disc to complete the hub assembly. Two 1/4" ID collars with setscrews
are included to hold the bearings into their pockets and lock the axle in place
on the motor/generator frame. Since the inexpensive variety of cold rolled
steel rod used here is not exact diameter, it had to be chucked up in a drill
press and buffed with emery paper to get everything to slide on smoothly.
![[frame]](./thumb/pmg/axle_1-t.jpg)
Frame:
One end of the motor/generator frame is the armature assembly itself. The other
end is another piece of 3/8" plywood. The base was cut 4 inches long from a
piece of 1"x12" board. This piece was cut to taper from 6-1/2" on the wide
(armature) end to 4-1/2" on the thin end, so it would be pretty. The end pieces
are held onto the base with wood screws. Rubber lamp base feet were screwed in
place at each corner on the underside of the frame end pieces. (Pilot holes
were drilled first to avoid splitting the plywood.)
![[frame]](./thumb/pmg/frame_1-t.jpg)
![[frame]](./thumb/pmg/frame_2-t.jpg)
Bearings:
The bearings are high speed ball type 3/4" OD x 1/4" ID, with good thrust
capacity (Fafnir S3KDD). They are held in place by setscrew collars on the axle
shaft. The collars hold them in 3/4" pockets cut into the outside faces of the
frame end pieces with a Forstner bit. With the pockets cut on the outside
faces, not only is the axle locked in place on the frame, the frame pieces are
held together by the tension of the collars holding the bearings into their
pockets.
![[bearings]](./thumb/pmg/bearing_1-t.jpg)
![[bearings]](./thumb/pmg/bearing_2-t.jpg)
Coil Assembly:
The motor/generator uses twelve 1.125" diameter, 0.25" thick, 90 turn, 21 AWG
enameled magnet wire round coils, wound on the previously described coil winder
around a 0.375" diameter polystyrene tube. All coils were wound in the same
direction and so that the last turn comes out on the same side of the coil as
the first turn. (Other than for those requirements, the wire layering pattern
is somewhat random.)
For each coil, the wire extending from the first turn was arbitrarily chosen to
be the "positive" coil lead, and a small loop was twisted in its end in order
to identify it after removing the coil from the winder. Prior to removing a
coil from the coil winder a few inches of fiber reinforced strapping tape was
wrapped around the circumference of its windings to hold them in place. The
reinforced tape was chosen because it holds well, even when moist, and also
because it tears uniformly lengthwise so that a width of tape that covered the
spread of the coils but did not adhere to the coil forms could easily be
obtained without having to actually try to cut the tape lengthwise. Once the
windings were taped in place the wire extending from the spool was cut,
(becoming the "negative" coil lead), and the coil was removed from the winding
form, with no danger of the coil unwinding itself. The 0.375" center tube was
then pressed out of the coil.
To keep coils from unraveling while applying the tape wrap, the nail which
holds the crank handle in the start position was reinserted in its hole in the
winder frame to stop the coil form from turning, and rubber bands were placed
on the wire spool spindle so that they were snug against each side of the
spool, thereby maintaining enough drag to keep the tension in the wire from
turning the spool. The rubber band tensioners were left in place during the
winding operation.
![[coils]](./thumb/pmg/winding_1-t.jpg)
![[coils]](./thumb/pmg/winding_2-t.jpg)
![[coils]](./thumb/pmg/winding_3-t.jpg)
Once twelve coils were formed, a paste of activated polyester resin and the
cast iron leavings from a break drum lathe was mixed and used to fill the coil
center holes, then left to harden. After the coil filling paste had hardened,
each coil was dipped in activated polyester resin, then hung and the resin
allowed to drip off and leave a thin coating over the coils, which then
hardened to completely seal the coil assembly.
![[coils]](./thumb/pmg/winding_4-t.jpg)
![[coils]](./thumb/pmg/winding_5-t.jpg)
![[coils]](./thumb/pmg/winding_6-t.jpg)
After the coil assemblies hardened, the small loop was cut off each coil's
positive lead, the enamel scraped back for about an inch from the cut end, and
a piece of red insulation 20 AWG solid core copper hookup wire about 10 inches
long was stripped of about an inch of insulation and soldered to each barred
coil lead. After the positive leads were each connected to their piece of
hookup wire, black insulation 20 AWG solid core was similarly attached to each
negative lead. A piece of heat shrink tubing was slid down both leads of each
coil and shrunk in place over the splices, leaving the coils ready for
attachment to the armature frame.
![[coils]](./thumb/pmg/winding_7-t.jpg)
Coil Mounting:
To maintain symmetry for the electrical connections, the coils were mounted on
the armature frame backing iron ring so that the face of a coil from which the
leads extend was placed against the frame, and the leads all extended radially
outward relative to the shaft hole. The coils were set in place according to a
scallop cut paper pattern; initially sticking them down with a glob of hot melt
glue. After the coils were hot melt glued in place the paper placement pattern
was removed, and a thin cardboard dam, lined with waxed paper (which does not
stick to hardening polyester resin), was taped in place, surrounding the coils
with about 3/16" clearance from their outward edges. Similarly a waxed paper
covered thin cardboard tube was inserted in the shaft hole. With the armature
frame lying flat and level, the area inside the dam was poured with activated
polyester resin to a depth of about 1/8", making sure that the liquid resin
completely surrounded each coil. When the resin hardened, the cardboard dam and
shaft hole plugs were pulled away, leaving the coils permanently attached to
the armature frame.
Note in the photo showing the paper coil placement pattern, that the armature
frame has been predrilled for the coil lead wires and phase wire connection
screw platforms. (This would be very difficult to do after the coils were
attached.) Note also that the coils were placed so that their leads align with
one of the two small holes between the sets of two larger holes in the
predrilled hole pattern. The small holes are for passing the lead wires
through the armature frame. The larger holes are for the screws which mount the
phase wire connection platforms to the back of the armature frame.
![[mounting]](./thumb/pmg/coil_mount_1-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_2-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_3-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_4-t.jpg)
Coil Lead Connection:
The coil leads are passed through their adjacent feed through holes in the
armature frame and connected to the phase lead screw connector platforms by
soldering them to tabs on the underside of the screw platforms. To allow for
consistent phase lead wire connection, the coil lead wires are connected in
repeated red/black order all the way around the armature frame.
The phase lead screw connector platforms themselves snap into a pair of nylon
standoffs, and the standoffs are mounted on the backside of the armature frame
with 4-40 brass screws and nuts. Each platform has 4 solder tabs, allowing two
coils to be connected. So, six platforms total were required to connect all 12
coils.
![[connections]](./thumb/pmg/connection_5-t.jpg)
![[connections]](./thumb/pmg/connection_3-t.jpg)
![[connections]](./thumb/pmg/connection_1-t.jpg)
![[connections]](./thumb/pmg/connection_2-t.jpg)
Final Assembly:
The motor/generator is assembled by screwing the armature frame and the
opposite end bearing support to the base block, inserting the bearings into
their pockets in the bearing supports, sliding the 1/4" steel rod axle through
the shaft hole in the bearing on one of the bearing supports, sliding the rotor
hub onto the shaft end between the armature frame and opposite end bearing
mount so the rotor magnets face the armature coils, then sliding the shaft on
through the second bearing and slipping a set screw collar onto each end of the
shaft, positioning the shaft for the desired extension of the shaft through the
bearings, sliding the set screw collars up to the bearings and tightening their
set screws to lock the shaft in place, and finally positioning the rotor on the
shaft and tightening its shaft screws to clamp the rotor in place on the shaft.
During assembly you need to be careful to not let the rotor magnets cause the
unclamped rotor to jump down the shaft and hit the armature coils. Even with
ferrite magnets the attractive force is significant. If you use neodymium
magnets the attraction could well be strong enough to cause the components to
slam together hard enough to damage the magnets, the coils, or your fingers
(no joke). Probably the easiest way to deal with the problem is to immediately
tighten one of the rotor hub screws after the shaft is inserted though the
hub and both bearings, then slide the set screw collar on to the end of the
shaft opposite the armature frame up to the bearing and tighten its set screw.
The placements of the shaft and rotor won't necessarily be correct, but the
rotor will be trapped in place and position adjustments are easy to make safely
from that point. Once everything is properly positioned, give all the screws on
last tightening check.
There is an optimal distance for the separation between the rotor magnets and
the armature coils. For the purposes of building a model like this you can
consider that to be about as close as possible without the magnets hitting the
coils when the rotor turns.
The rotor and armature should be as parallel as possible. To improve its
parallel alignment with the rotor, a small adjustment of the armature frame was
made by loosening the screws holding the frame to the base, placing two narrow
strips of 0.01" thick polystyrene sheet plastic face to face in the upper side
of the gap between the armature frame and the base block, then retightening the
frame screws.
![[mot/gen]](./thumb/pmg/mot_gen_1-t.jpg)
![[mot/gen]](./thumb/pmg/mot_gen_2-t.jpg)
![[mot/gen]](./thumb/pmg/mot_gen_4-t.jpg)
Phase Wiring:
In a three phase system, the phases are electrically 120 degrees
apart. But, the armature coils are not (necessarily) physically spaced at 120
degree intervals around the armature frame. The total number of coils in the
armature and the number of coils used for each phase affects the physical
placement of coils around the armature frame.
For the motor/generator being described here, there are twelve armature coils,
which allows 4 coils to be connected in series for each of the three phases.
(Thus, each phase can provide four times more voltage than would be obtained
using a single coil for each phase.) And, 12 coils means they will be spaced at
thirty degree intervals around the 360 degree perimeter of the armature frame.
The phases are referred to as A, B, C, and, starting from the right one of the
topmost pair of coils on the armature frame, the coils are identified in the
clockwise direction as follows: A1, B1, C1, A2, B2, C2, A3, B3, C3, A4, B4, C4,
where C4 is the left one of the topmost pair of coils. Each indexed letter
of the alphabet refers to one of the coils in the group of coils that comprises
on phase coil set, e.g., coils A1, A2, A3, and A4 are the coils wired together
for phase A.
Although each individual coil is only 30 degrees from its closest neighbors,
the correspondingly numbered coils for each adjacent phase are, in fact, 120
degrees apart, e.g., four 30 degree spaces separate coils A1 and B1, etc. Thus,
adjacent phases are 120 degree apart, with phases A and B being 120 degrees
apart, and phases A and C being 240 degrees apart, as is required for a three
phase system.
The number and spacing of magnets around the rotor also enters into how the
phase coils are wired. To work properly, at any instant in time each coil in a
phase must be contributing current to the phase of the same polarity and
magnitude. Whether a coil is being energized by the north pole or the south
pole of a magnet determines the polarity of the current produced in the coil.
The distance in its rotating path a magnet is from a coil determines how much
it contributes to the magnitude of the current generated in the coil. (A
changing magnetic field is required to generate current in a wire coil, and
motion of the magnets results in a changing magnetic field.)
Because there are alternating north and south magnet poles, the separate phase
coils cannot be simply connected in series, as the resulting currents generated
in the individual coils in a phase will not match. The phase wiring used for
the motor/generator being constructed here is as shown in diagram below. The
details of why the connections are made as they are can be found in the "How's
it Work?" section.
![[phase wiring]](./thumb/pmg/mot_gen_phs_1-t.jpg)
Besides how far away from a coil a magnet is in its rotating path, the gap
separating the rotor magnets and armature coils when they are aligned also
determines the magnitude of the current generated. There are some constraints
on how close magnets should be to the coils, but, basically, we're just going
to get them as close as the wobbles in construction will allow without anything
banging against anything else. Some of the details on determining the gap
distance can also be found in the "How's it Work?" section.
![[phase wiring]](./thumb/pmg/phase_wiring_1-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_2-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_3-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_4-t.jpg)
Preliminary Testing:
Spin it and it makes wiggles. Apparently wiggles of the correct phase
separations at that!
![[testing]](./thumb/pmg/testing_2-t.jpg)
![[testing]](./thumb/pmg/testing_1-t.jpg)
![[testing]](./thumb/pmg/testing_3-t.jpg)
![[testing]](./thumb/pmg/testing_4-t.jpg)
![[phase A-B]](./thumb/pmg/phase_a-b-t.jpg)
![[phase B-C]](./thumb/pmg/phase_b-c-t.jpg)
![[phase A-C]](./thumb/pmg/phase_a-c-t.jpg)
Upgrades:
Over time a few features have been added to the motor/generator to make its use
and testing a bit easier.
Handcrank:
![[hand crank]](./thumb/pmg/pmgcrank_01-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_02-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_03-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_04-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_05-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_06-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_07-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_08-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_09-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_10-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_11-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_12-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_13-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_14-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_15-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_16-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_17-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_18-t.jpg)
Handle:
![[hand crank]](./thumb/pmg/pmghandle_01-t.jpg)
![[hand crank]](./thumb/pmg/pmghandle_02-t.jpg)
![[hand crank]](./thumb/pmg/pmghandle_03-t.jpg)
Change ferrites to neodymium magnets:
![[new magnets]](./thumb/pmg/neodymium_01-t.jpg)
![[new magnets]](./thumb/pmg/neodymium_02-t.jpg)
![[new magnet test]](./thumb/pmg/neotest_01-t.jpg)
![[new magnet test]](./thumb/pmg/neotest_02-t.jpg)
3-phase rectifier:
![[3 phase rect]](./thumb/pmg/3phsrect_01-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_02-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_03-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_04-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_05-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_06-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_07-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_08-t.jpg)
![[3 phase rect test]](./thumb/pmg/recttest_01-t.jpg)
![[3 phase rect test]](./thumb/pmg/recttest_02-t.jpg)
How's It Work?:
OK, if you go through the whole thing, this will seem perhaps a bit long winded
and maybe a bit spotty description of how permanent magnet motor/generators
work. But, the good news is if you just want to know how to figure out the
number of coils you need for a given number of magnets and how to hook them
up to successfully produce your own single-phase or polyphase motor/generator,
you're in luck! We'll cover that right off the bat with a set of simple
instructions and formulas. What follows the basic "how-to" information
just fleshes out the details of what you're doing and why you're doing it.
One caveat for the rote instructions. They do assume you know, or know how
to determine, the polarity of your coil leads for proper connection. Store
bought coils are likely marked for polarity. If you plan to wind your own
coils, (and why wouldn't you and miss all the fun?!), then here, without
explanation, is how to establish their polarity. Wind them all identically,
all coils with turns in the same direction and filling the form you wind
them on in the same way. Choose the end of the wire you started with and,
arbitrarily, call it the positive (+) polarity lead, and call the other
end of the wire coming from the coil the negative (-) lead. Don't worry
about which way you start making the turns in your coils, just do what is
easiest for your set up. Just be consistent from coil to coil, and all
will be fine. Why consistency without measurement works, we'll cover later.
Now, the instructions and formulas given below don't give all possibilities
for coil connection and magnet arrangement you might encounter. But, they
do provide the information you need to make practical, working, permanent
magnet single-phase and polyphase motor/generators.
The same formulas work whether you're building a single-phase or a polyphase
motor/generator. But, they become so simple in the single-phase case that
we'll cover the single-phase motor/generator separately from the polyphase
motor/generator.
Before getting to the actual construction instructions, first let's take
a look at a diagramming method to show motor/generator coil connections.
The technique, presented in the section that follows, is adapted from some
of the figures in a well know book on electric motor repair by Robert
Rosenberg [3]. A few other books on the
subject of permanent magnet motor/generator design and motor design
in general are listed in the references [4,
5,6].
Diagramming motor/generator phase coil connections:
Once you're decided on how many coils to use in your motor/generator, draw
a small rectangle, one for each coil, in a row across a piece of paper. To
represent the coil leads draw a short line down from the bottom corners
of each of your rectangles. You can, but it isn't absolutely necessary,
make a dot near the left lead line to indicate the positive polarity coil
lead for each rectangle. And, for each phase in your motor generator, label
the coil rectangles in a repeating sequence.
Traditionally, phases are labeled by the letters of the alphabet. So, given,
for example, nine coils to use in a 3-phase system you would repeat A,B,C in
sequence three times, as A,B,C,A,B,C,A,B,C. Or, if you were designing, say,
a 5-phase system, you would label your boxes, in sequence, with the letters
A though E. If you like, you can identify each phase coil group by appending
numbers to the letters. In our case of nine coils in a 3-phase system, the
coil box labels would then be, in sequence, A1,B1,C1,A2,B2,C2,A3,B3,C3.
Now, regardless of whether you plan to build a single-phase or a polyphase
motor/generator, due to the alternating north and south poles of the
rotor magnets, when operating, the direction of current through each coil
will be the opposite of the direction of the current through the coil that
precedes it. (This is the origin of the term Alternating Current (AC). More
on that in the detail sections that follow.) So, under each coil box, between
the lead lines, draw a small arrow to represent current direction. Start from
the left box with an arrow pointing to the right, and alternate arrow direction
with each box that follows.
And, that's it! The complete starting point diagram for a nine coil, 3-phase
motor/generator is given in figure 1. For a motor/generator with more or less
coils, just draw more or less boxes.
Armed with the base of a diagramming technique for producing a simple picture
of what we want to build, we can now get on with how to actually find the
number of coils we need, and how to hook them up.
![[coil diagramming]](./big/pmg/fnfig-01.jpg)
Coil count and connections for a single-phase motor/generator
- Dig through your junk box and find all your magnets.
- Make piles of the same types of magnets
- Choose the pile containing the type of magnet you want to use in
your single-phase motor/generator.
- Count the magnets in the chosen pile. If it is an odd number,
toss one magnet back in the junk box, or go find another one,
so that you end up with an even number of magnets.
- Make the same number of coils as you have chosen magnets.
- Lay your coils out in a row so that their positive lead is
on the same side of each coil in the row, and connect them
in series so that the negative lead of the first coil connects
to the negative lead of the second coil, the positive lead of
the second coil connects to the positive lead of the third
coil, and so on. The proper connection is simple to show
using the diagramming technique presented above. Just draw
lines to connect the coil boxes so that the lead nearest the
head of one box's arrow connects to the lead nearest the tail
of the next box's arrow (figure 2). Physically making this
connection relative to the positive leads as drawn on your
coil diagram guarantees the alternating current flow directions
in the coils do not oppose each other.
![[single phase coils]](./big/pmg/fnfig-02.jpg)
- Build your motor/generator with magnets alternating north and
south poles evenly spaced around it's rotor, and coils evenly
spaced around it's armature, as, for example, shown in figure 3
for an eight magnet, 8 coil, single-phase motor/generator.
![[single phase build]](./big/pmg/fnfig-03.jpg)
OK, there is a bit of a misleading implication above. In steps (6)
and (7) above there is no differentiation between connecting coils for
a single-phase motor or for a single-phase generator. The connection
will work just fine as described for a generator. And, in fact, as
described, the connection will also work for a motor. Connect an AC
power source to a motor/generator with an armature wired as in figure 2,
and it can be made to spin via the input power. But, it will not self
start. You will need to give it a bump to get it to go. A single-phase
motor can be connected to self start. We'll leave that discussion until
after we talk in more detail about polyphase motor/generators.
Coil count and connections for a polyphase motor/generator:
- Dig through your junk boxes and find all your magnets.
- Make piles of the same types of magnets
- Choose the pile containing the type of magnet you want to
use in your polyphase motor/generator.
- Count the magnets in the chosen pile. If it is an odd number,
toss one magnet back in the junk box, or, go find another one,
so that you end up with an even number of magnets.
- Decide how many phases you want to use in your polyphase
motor/generator. Most everyone on the planet chooses three,
and, I'm going to choose 3 for this discussion, so you might
as well, too. You don't have to choose three phases, but at
least choose an odd number. (To show this technique does
generalize I'll diagram hooking up a five-phase motor/generator
after the 3-phase discussion.)
- Calculate the number of coils required:
For a given number of phases, N, you need N coils per magnet
pair in your N-phase motor/generator.
For a count of M magnets (often referred to as poles), with M
an even number, we have M/2 magnet pairs.
So, for an N-phase motor/generator with M poles the number of
coils required, C, is:
C = N*(M/2).
I found 8 magnets in my junk box when I set out to write this.
So, for a 3-phase motor/generator the number of coils we want
to wind is:
3*8/2 = 12.
- Calculate the number of coils per phase:
For C coils and N phases, the number of coils per phase is C/N.
Here, for our 8 pole, 3-phase motor/generator we get 12/3 = 4
coils per phase. This means you will be connecting three
groups of 4 coils each in your motor/generator.
- Select the motor/generator wiring configuration:
For a 3-phase system, there are two primary types of polyphase
motor/generator connections, Delta, and Y (also know as a Star
connection). For a Delta connection, the phases are connected
in a triangular configuration. In a Y connection the phases are
connected in 3-armed, or "Y" shaped configuration. The Delta
configuration is more efficient for low rpm operation, and we'll
choose that for now. The Y configuration will be covered in the
details discussion that follows these rote instructions and formulas.
- Diagram the phase connections:
Using the previously described diagramming technique (figure 1),
each of the four coils in the 3 phase groups is connected in
series just as in the single-phase motor/generator so there is
proper current flow through the group. Draw lines so they connect
(+) to (+) and (-) to (-) polarity coil connections for each of
the phase coil groups (figure 4). You can use the "follow the
arrow" method with each phase group the same as described in step
(6) for the series connection of all coils in the single-phase
motor/generator. Note carefully how the B phase starts on phase
coil B2, not coil B1. This is because the first B phase coil who's
current direction matches the current direction of the first
coils in the A and C phase coil groups is B2, not B1.
![[polyphase groups]](./big/pmg/fnfig-04.jpg)
Once the A,B, and C, phase coil groups are connected, then the
groups are connected to form the chosen Delta or Y configuration.
For a three-phase Delta connection the end lead of the A phase
coil group is connect to the starting lead of the C phase coil
group, the end lead of the C phase coil group is connected to the
start lead of the B phase coil group, and the end lead of the
B phase coil group is connected to the start lead of the A phase
coil group, as diagrammed in figure 5. Again, as pointed out in
step (9) above, note the starting lead for the B phase coil
group comes from coil B2, not coil B1.
![[polyphase connections]](./big/pmg/fnfig-05.jpg)
- Build it. Figure 6 shows an example physical diagram for a three-phase,
8-pole, 12-coil, Delta connected motor/generator.
![[polyphase build]](./big/pmg/fnfig-06.jpg)
If you use your motor/generator in motor mode and want it to spin in the opposite
direction from what you will find with the motor/generator design given here,
you can reverse any two of the input phase connections, and the motor will run in
reverse. We'll see why that is later. (And, of course, you could also physically
turn the motor around 180 degrees so that the end of the shaft facing you becomes
the end of the shaft pointing away from you.)
There is no issue with self starting of polyphase motors. Connect three-phase
power to a 3-phase motor/generator and it will run as a motor without any of
the startup connection tricks required for a self starting single-phase motor
to be discussed later.
Of magnets and wires and such:
Getting into the spin:
First thing, magnets. Most everyone has played with magnets at one time or
another. Point the opposite poles of two magnets at each other, north to south,
and they attract. Point the same poles at each other (north to north, or south
to south) and they repel. Interaction of the magnetic fields produced by the
magnets is what causes the attraction and repulsion effects observed for a pair
of magnets.
The same as it is for the magnetic field of the earth, the magnetic field of
a simple bar magnet is described as lines of magnetic flux which extend from a
magnet's north pole to its south pole (figure 7). (It might be good to note here
that the north geographic pole of the earth is actually a south magnetic pole.
Which explains why the north pole of the magnet in a compass points toward
the earth's geographic north pole.)
![[magnet flux lines]](./big/pmg/fnfig-07.jpg)
Considering the magnet flux lines as drawn in figure 7, magnetic attraction
and repulsion can be viewed as the interaction of the arrows (or vectors)
giving the direction of the flux lines from north pole to south pole. When two
north or two south poles are brought next to each other, the arrows from one
magnet's pole point in the opposite direction of those from the other magnet's
pole, and, hence, "collide," pushing each other away, causing the repulsion
effect. But, when a north pole and a south pole are brought together, the
arrows point in the same direction, and one set "sucks" the other set along,
much like two streams of water flowing in the same direction, which causes the
attraction effect. (This is, of course, just a description for visualization
purposes.)
Magnetic repulsion and attraction are the basis of operation for an electric
motor. By proper alignment and timing of magnetic fields, the parts of an
electric motor can be made to push and pull on each other so that a smooth
continuous motion is obtained.
Besides having a magnet handy, another way to generate a magnetic field is to
run an electric current through a piece of wire. The flow of current through
a wire produces lines of magnetic flux around the wire just like the lines
of magnetic flux produced by a magnet. The lines of flux are produced such that
when you point your left thumb
along the wire in the direction of current flow
through the wire, your left fingers will curl around the wire in the same
direction as the lines of flux around the wire, i.e., you finger tips will
point in the same direction as the arrows seen in a diagram of the flux lines
(figure 8).
![[left hand rule]](./big/pmg/fnfig-08.jpg)
Obviously, if the direction of current through the wire is reversed, then you
have to point your left thumb in the opposite direction, and, as shown by the
curve of your fingers, the lines of flux around the wire will be in the
opposite direction, effectively changing the polarity of the magnetic field
around the wire.
We aren't going to get deeply into what constitutes the "real" direction of
current flow in a wire. As has been pointed out above, consistency is what
counts. Make your favorite assumption, use it without fail, and all will be
well.
Here we'll consistently consider current flow to be from the negative terminal
of a power supply to the positive terminal of a power supply. That means we're
looking at electron flow, and not current flow as it was originally assigned
to be from positive to negative for the first electric batteries, (a concept
based on Benjamin Franklin's earlier description of two types of electricity,
"positive" and "negative," which, well, frankly, some would say he got
backwards). Engineers and physicists can argue about what is really going on
all they want, and we'll just get on with the task at hand. Symmetry, which
we'll talk about more a bit later, is the key to why, for practical purposes,
the initial choice doesn't really matter. In fact, if you are more comfortable
considering current flow to be from positive to negative then consistently
use that idea, and instead of using the left-hand rule as described above, just
use your right hand to apply the right-hand rule. Then following the curve to
your right finger tips will get you the same results as we've seen for the
left-hand rule. That's symmetry!
Now, the nature of magnetic poles around a straight piece of wire with current
flowing through it isn't immediately obvious. But, if you turn the wire into
a loop, the orientation of magnetic poles relative to the wire becomes more
clear. As shown in figure 9, with current flow from left to right and the loop
directed into the page, the flux lines circulate into the top of the loop and
out of the bottom. Comparing this to the flux lines seen for the magnet in
figure 7, we can see this implies the north pole of the loop's magnetic field
is at the bottom, and its south pole is at the top.
![[wire loop flux lines]](./big/pmg/fnfig-09.jpg)
The effect becomes more clear when there are multiple loops stacked on top
of each other to form a coil. Since the flux lines produced by each loop
combine in the same direction they produce a larger (and stronger) magnetic
field (figure 10). This is why more turns in the coil of an electromagnet make
for a stronger electromagnet.
![[wire coil flux lines]](./big/pmg/fnfig-10.jpg)
As can be seen in figure 10, the same repulsion and attraction of flux lines
can be had from the coil as from a real magnet. By reversing the direction of
current through the coil the orientation of its north and south poles is
reversed. And, by taking this action in to account, simple electric motors
can be devised. For example, with proper timing of the change in direction
of current through two coils, a magnet on an axle can be made to rotate
between the coils (figure 11).
![[simple electric motor]](./big/pmg/fnfig-11.jpg)
Going the other way:
OK, in the last section we made it as far as a good idea of how to make a
simple electric motor. A lot of details need to be filled in yet. Like, in
particular, how to control switching and timing of the magnetic fields, but
it's a definite start. And, with the information we put together there about
magnets and wires and such, we are in good shape to move ahead with an initial
description of how electric generators work.
As mentioned before, the aspects of physics we're looking at are symmetric.
So, just as running a current through a wire creates a magnetic field, moving
a magnet near a wire creates an electric current in the wire (figure 12).
![[magnet creates current]](./big/pmg/fnfig-12.jpg)
Of course, the more wires a moving magnetic field crosses, the more currents
that are generated, one for each wire (figure 13). And, when a wire is wound
in a coil, the effect is the same for each loop in the coil, except, because
the coils are connected, the multiple currents created as the magnetic field
passes over the coil windings add together. So, the more windings in the coil,
the more current generated as the magnetic field passes by (figure 14). This
is the basic idea behind an electric generator.
![[multiple wires multiple currents]](./big/pmg/fnfig-13.jpg)
![[coiled wire bigger current]](./big/pmg/fnfig-14.jpg)
Also, the stronger the moving magnetic field, the more current generated in any
wire it moves by. So, either by putting more turns in its coils, or by using
stronger magnetic fields, or both, the more power that can be produced from a
generator or utilized from a motor.
We've already see examples of making simple permanent magnet generators in the
coil count and connection sections above. So, let's continue on and investigate
a few more details that will lead us to an understanding of why we make the
connections we do as previously described for single-phase and three-phase delta
motor/generators, and also how to define connections for other than single and
three-phase systems.
Pick a phase, any phase:
OK, so what does "phase" mean, anyway? Well, it's another one of those words
that changes meaning with context. Regarding polyphase motor/generators, it
is often used interchangeably to describe two main features. It can mean one
of the multiple leads (or the lead's associated electrical waveform) in a
polyphase system, or it can mean the difference (measured in degrees) between
the peaks seen in the waveforms found in any two leads in a polyphase system.
For the second case that difference is more correctly referred to as the
"phase angle," which, here, is a term that relates to the notion of a rotating
magnetic field. The rotating magnetic field concept is at the heart of any
motor/generator system, be it single or polyphase.
That we are dealing with rotating magnetic fields seems easy enough to accept.
The devices we've been discussing have magnets that spin on an axle. So,
there it is, rotating magnetic fields. Pretty unavoidable, that. Of course,
as always, the devil is in the details.
Sinusoids:
Rotation implies circles. But, to draw a circle covering the 360 degrees of
each rotation to represent the motion over time of a motor/generator that may
be spinning at thousands of revolutions per minute wouldn't be too informative.
So, instead, we draw a sinusoid, which is just a way of displaying circular
motion in a linear diagram.
To see this, consider a simple machine consisting of a disc with a peg at its
edge parallel the disc's center axle, and a "T" shaped piece which has a slot
in its crossbar. The T-bar is laid on the disc so that the crossbar slot fits
over the peg, and the upright points down when the machine is looked at in
plan view. A guide aligned with the center of the disc is placed over the
T-bar upright so that while the peg on the disc can slide back and forth in
the slot in the T-bar crosspiece as the disc rotates, the T-bar upright can
move up and down, but not side to side. So, while the disc rotates, the peg
moves in a circular motion which forces the T-bar to move so that its end
travels up and down a distance equal to the diameter of the circle defined by
the motion of the peg (figure 15).
![[circle to line machine]](./big/pmg/fnfig-15.jpg)
If a pencil is attached to the end of the T-bar upright piece so that it will
leave a mark on a piece of paper placed under it, then, as the disc rotates the
pencil will draw a straight line with length equal to the diameter of the
peg circle each time the disc rotates. We can spin the disc until the pencil
wears out, but that is all we will see, a single vertical line. However, if
we move the paper parallel to the T-bar cross piece, we'll see something
quite different, that is, a repeating curve, called a sinusoid, which gives
the diameter of the peg circle via its amplitude, and repeats its waveform
across the paper through a number of cycles that relates to the rotational
speed of the disc and the speed of motion of the paper under the pencil
If we know the speed of the paper, then we can deduce the rotation speed of
the disc by counting the number of cycles in a given distance across the page,
equating distance to the time it took the paper to travel that distance, and
dividing the number of cycles see in the sinusoid over the given distance
by the equivalent time for that distance. The result is disc rotation speed
expressed as frequency in units of cycles (rotations) per chosen time unit.
If we arbitrarily designated the start (0 degrees) position as when the
peg is at its topmost position when the disc rotates, and start moving the
paper to the right just when the peg reaches that point, then the pencil
on our simple machine will trace out a sinusoid that represents the circular
motion of the disc as a "wave" that has a positive maximum value at the start
time position, drops to zero when the disc has rotated 90 degrees, reaches a
maximum negative value as disc rotates through 180 degrees, returns to 0 when
the rotation reaches 270 degrees, and climbs back to the maximum positive value
as the rotation goes though 360 degrees. The 360 degree rotation returns the
pencil to the maximum positive position, but a distance across the page that
equates to one rotation time, and the cycle repeats (figure 16).
![[creating a sinusoid]](./big/pmg/fnfig-16.jpg)
The time for a sinusoid to complete one rotation cycle is referred to as its
period (T). The number of cycles the sinusoid completes in a fixed time period
is referred to as its frequency (f). Traditionally the time period to count
cycles to determine frequency is one second, and frequency is expressed in
cycles per second or Hertz (Hz). Note that frequency is the inverse of period,
that is, divide 1 by the period value, and you get the frequency value, or,
divide 1 by the frequency value and you get the period value:
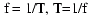 .
.
Rather than using spinning discs with sliding pencils to diagram rotations, the
trigonometric function cosine has been defined to represent just this motion.
In a mathematical formula the cosine function is given as cos(x), where the
argument x represents the degrees of rotation. The cosine function follows
the same form of curve as described by the pencil and disc arrangement of
figure 16; having a value of 1 for an argument of 0 degrees, a value of 0 for
an argument of 90 degrees, a value of -1 for an argument of 180 degrees, a
value of zero for an argument of 270 degrees, and returning back to 1 for an
argument of 360 degrees.
The amplitude of the curve drawn by the pencil and disc method is equal to
the diameter of the disc. But, since we have defined things to range
over plus and minus values, and the cosine function ranges from 1 to -1, we
multiply the cosine function by half the diameter (the radius) of the disc to
get the proper values for the curve relative to the degrees argument to the
cosine function. That is, if the diameter of the disc is A, then at any
particular degrees of rotation value, x, the proper height, h, of the sinusoid
is given by:
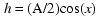
We can't make the mistake of thinking that the diameter of the disc mentioned
above has anything to do with the diameter of our motor/generator rotor disc.
The "diameter" we are really talking about is simply the amplitude of the
sinusoidal electrical waveforms applied to, or generated by, our
motor/generator. In fact, without any loss of usefulness, we can drop the
division by 2 in the amplitude factor, and just use the parameter A alone to
indicate we want to allow sinusoids with an amplitude range other than from
-1 to +1, assume the value of A will be chosen correctly when necessary, and
go with the slightly simpler equation:
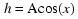
Now we almost have a mathematical formula that can be used to diagram the phase
waveforms seen in our motor/generators. But, there is still that matter of x,
the unknown angle. If we just wanted to plot one sinusoid, then varying x from
0 to 360 and plotting the result for h as the y value in an x-y plot would do
fine. But, that isn't going to give us what we need when it comes to looking
at the phase angle between phase waveforms. Also, often we won't want to plot
with degrees on the x axis of our plots, but rather with time. Fortunately,
since we are dealing with known rotation speeds, (i.e., the frequency of the
sinusoidal waveforms in question, e.g., the 60 cycles per second (60 Hz) for
commercial power found around here), that's relatively easy to figure out.
So, back to considering imaginary spinning discs and sliding pencils for a bit.
Another way of measuring angles is in radians. There are
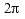 radians in 360
degrees (making one radian approximately 57.297 degrees). So, one rotation of
the disc in figure 15 means the peg which moves the crossbar sweeps through an
angle of
radians in 360
degrees (making one radian approximately 57.297 degrees). So, one rotation of
the disc in figure 15 means the peg which moves the crossbar sweeps through an
angle of 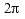 radians.
Radian measure is just a scaling factor different from degree measure, and the
cosine function can be defined to use radians as an argument as well as degrees.
For the time being we'll use that definition. It might seem an added confusion
to switch from degrees to radians, but, that is really just a matter of what you
are used to. We gain something by switching to radian measure, that is, when
coupled with the concept of radial velocity, the ability to use time as the
argument to the cosine function.
radians.
Radian measure is just a scaling factor different from degree measure, and the
cosine function can be defined to use radians as an argument as well as degrees.
For the time being we'll use that definition. It might seem an added confusion
to switch from degrees to radians, but, that is really just a matter of what you
are used to. We gain something by switching to radian measure, that is, when
coupled with the concept of radial velocity, the ability to use time as the
argument to the cosine function.
Radial velocity (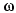 )
is a measure of the speed of rotation of a disc in terms of radians per second,
rather than cycles per second. Again, we aren't really talking about speed of
rotation of a disc, but the "speed" with which a sinusoidal waveform
completes its repeated identical excursions. The concept of radial velocity
still applies, since that sinusoid has the same circular motion related form
as the one produced by the disc and pen method of figure 15. In either case,
multiplying the radial velocity by time (measured in seconds) gives us radians
as a proper argument to the cosine function, and, thus, knowing the radial
velocity, we can plot our sinusoid against time on the x-axis of an x-y plot,
rather than degrees. That brings us to a new form for our equation:
)
is a measure of the speed of rotation of a disc in terms of radians per second,
rather than cycles per second. Again, we aren't really talking about speed of
rotation of a disc, but the "speed" with which a sinusoidal waveform
completes its repeated identical excursions. The concept of radial velocity
still applies, since that sinusoid has the same circular motion related form
as the one produced by the disc and pen method of figure 15. In either case,
multiplying the radial velocity by time (measured in seconds) gives us radians
as a proper argument to the cosine function, and, thus, knowing the radial
velocity, we can plot our sinusoid against time on the x-axis of an x-y plot,
rather than degrees. That brings us to a new form for our equation:
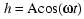
A bit more work with this expression will lead us to the ability to check the
phase angle between sinusoids at a particular time, which is a lot easier to
work with than trying to check phase angles related to portions of a cycle,
which would be the case if we used degrees and frequency in our equations,
rather than radians and radial velocity.
Before we move on to checking phase differences, there is one more important
relationship to note, the connection between frequency and radial velocity.
The unit Hz (cycles per second) refers to how many rotations per second we
see for our rotating disc or how many full excursions per second we see in
our sinusoidal wave form. In either case, one rotation or one sinusoidal
excursion, we can equate the frequency to sweeping an angle of 360 degrees
with every cycle. So, for example, we could say that a 60 Hz signal is also
a 60*360 = 21600 degrees per second signal. Of course, that isn't a very useful
piece of information. We need some way to relate the degrees of sweep per
second for a signal frequency measured in cycles per second to radial velocity
so that we can apply the value we know, frequency, in our equation that uses
radial velocity and time. Radians to the rescue!
To use frequency in our equation in
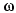 and t, we need to
convert from frequency to radial velocity so that the multiplication by t will
give the proper value in radians. That we can do by noting, as pointed out
before, one revolution is
and t, we need to
convert from frequency to radial velocity so that the multiplication by t will
give the proper value in radians. That we can do by noting, as pointed out
before, one revolution is
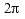 radians, and also
that one cycle in frequency is one revolution, then multiply the appropriate
factors together so that the units cancel out to give radians per second, the
proper units for
radians, and also
that one cycle in frequency is one revolution, then multiply the appropriate
factors together so that the units cancel out to give radians per second, the
proper units for 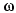 ,
i.e,
,
i.e,

That leads us to another form for our sinusoidal equation:
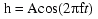 ,
,
which allows us to plot our waveforms against time, while using frequency in
the argument to the cosine function.
So, all that verbage just to explain a factor of
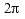 ? Well, yes and no.
The warm up to expressing circular motion as a sinusoid will prove useful later,
when we look at making connections in a polyphase motor/generator in terms of
vector sums. At least we are done here now, and can get on with the next phase
in our discussion.
? Well, yes and no.
The warm up to expressing circular motion as a sinusoid will prove useful later,
when we look at making connections in a polyphase motor/generator in terms of
vector sums. At least we are done here now, and can get on with the next phase
in our discussion.
Phase vs. phase:
I'll state in advance the discussion here may get a little confusing. This is
because, as mentioned before, phase is one of those words that changes meaning
with context. The main uses for "phase" here will be to mean one of the
input/output wires to a motor/generator or one of the phase coil groups as
described earlier in the polyphase coil count and connection section (these
two meanings are basically synonymous), or also to mean the sinusoidal
waveform found in an input/output wire or phase coil group. Another potential
confusion may come in use of the terms "phase difference" and "phase angle."
The phase difference is the difference between phases. (Well, duh!). That
difference is usually measured as an angle, and, so, it is often referred to
as phase angle. More correctly, the phase angle is the value of the phase
difference, but, whatever, the two terms are used interchangeably elsewhere,
and will be here, too.
So, OK, that being that, we're just about there. We have a cosine equation we
can use for generating sinusoids, in which we can use variables we know or can
determine, time and frequency. Now we need a way to include phase difference
into our equation.
The phase difference between two sinusoids is the separation in angle between
the same relative point on the waveforms. We measure the difference as an angle
because the sinusoids are representations of circular motion and the difference
between two points on a circle is normally expressed as an angle. That angle
is not quite enough information to describe the difference. We also need to
know which waveform comes first. That association is described using the terms
"lead" and "lag." When one waveform leads another waveform then the first one
reaches the end of a cycle before the second one. When one waveform form lags
another waveform, then the first waveform reaches the end of a cycle after the
second one (figure 17).
![[lead vs. lag]](./big/pmg/fnfig-17.jpg)
To include a lead or a lag in our cosine equation, we simply subtract or
add a phase angle in the main angle argument. Careful here. The relationship
isn't quite intuitive. If we have two sinusoids rotating with the same
frequency, and only apply the phase correction to one of the two, then to
force a lead by the uncorrected waveform over the uncorrected waveform we
subtract the phase angle from the corrected waveform, and to force a lag of the
uncorrected waveform we add the phase angle to the corrected waveform (figure
18).
![[cosine lead vs. lag]](./big/pmg/fnfig-18.jpg)
We've now reached the final form of our cosine equation:
 ,
,
where the phase angle,
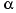 , may be positive
or negative, and, as used here, should be expressed in radians. If
, may be positive
or negative, and, as used here, should be expressed in radians. If
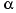 is provided
in degrees, then multiply by
is provided
in degrees, then multiply by
 and divide by 180 to
convert degrees to radians, which leaves us with the same basic form of the
equation:
and divide by 180 to
convert degrees to radians, which leaves us with the same basic form of the
equation:
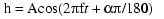 ,
,
In a later section we will be introducing another multiplication factor for the
argument in f and t. But, for now we'll ignore that and move on to look at
expressing the full set of phase angle relationships for a polyphase
motor/generator via our latest equation.
In general, to make a set of plots for phase comparisons, we need an equation
for each sinusoid, with each equation expressing the amplitude, frequency,
and phase difference for its associated sinusoid. For arbitrary sinusoids
each equation would have a completely different set of arguments and
multiplication factors. For example, the equation set for three arbitrary
sinusoids, A,B,C, would be, with the phase angle expressed in radians:

Using these equations we could compare three sinusoids of arbitrary magnitude,
arbitrary frequency, and arbitrary phase angle at any point in time. But, here
we make two simplifying assumptions, that the magnitude of each sinusoid is the
same, and the frequency of each sinusoid is the same. Note that with the
identical magnitudes assumption we can set the magnitude factor to 1 in each
equation with no loss in generality. Also, note that with the identical
frequency assumption time is no longer a critical factor if we are only
comparing phase differences, and we can make the comparisons at any arbitrary
rotation angle, say,
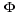 . We can make one
more simplification that has its origin in standard practice rather than
physics, which is when comparing phases, we assume the phase angle for the
first phase is zero, and adjust the other phase angles accordingly. That gives
us, in our three phase case, the following simplified equation set:
. We can make one
more simplification that has its origin in standard practice rather than
physics, which is when comparing phases, we assume the phase angle for the
first phase is zero, and adjust the other phase angles accordingly. That gives
us, in our three phase case, the following simplified equation set:

So, now we just need the phase angles for the B and C sinusoids.
In a polyphase motor/generator the sinusoidal waveforms found in each phase
have a fixed angular relationship, determined by the number of phases. Each
phase leads the next one by the same angle. That phase difference, P, is
simply one full cycle expressed as an angle, 360 degrees or
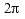 radians, divided by
the number of phases. Using degree measure:
radians, divided by
the number of phases. Using degree measure:
P = 360/N.
Thus, for a three-phase system, we get a fixed phase angle of P = 120 degrees.
Of course, it would be just a little to simple if we could use 120 degrees, (or
120 /180 radians), for
the phase angles in our simplified equation set. If we draw three sinusoidal
waveforms, A,B,C, each leading the next by 120 degrees, (figure 19) we can find
the required phase angle values for our set of cosine equations by examining
the plots.
/180 radians), for
the phase angles in our simplified equation set. If we draw three sinusoidal
waveforms, A,B,C, each leading the next by 120 degrees, (figure 19) we can find
the required phase angle values for our set of cosine equations by examining
the plots.
![[3-phase lead/lag]](./big/pmg/fnfig-19.jpg)
We know we want a phase angle of zero for waveform A. And, traditionally, we
also use positive value phase angles. That means we will look for appropriate
phase lags to define our phase angles. The positions where the phase A
and B waveforms reach their maximum value within one full cycle, with A lagging
B, is at
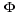 = 120 degrees for
B and
= 120 degrees for
B and 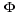 = 360
degrees for A. That gives us a phase difference between A and B of 360 - 120 =
240 degrees, which we use as the phase angle for the B waveform cosine
equation. Similarly, the phase difference for A lagging C is 360 - 240 = 120
degrees, which we use as the phase angle for the C waveform cosine equation.
That gives us the following equation set:
= 360
degrees for A. That gives us a phase difference between A and B of 360 - 120 =
240 degrees, which we use as the phase angle for the B waveform cosine
equation. Similarly, the phase difference for A lagging C is 360 - 240 = 120
degrees, which we use as the phase angle for the C waveform cosine equation.
That gives us the following equation set:

which is the standard form for three-phase equations. To determine lag
values from the given phase lead differences of 120 degrees without having to
plot the waveforms, we can just note, as pointed out earlier, (figure 18), that
a phase lead relationship between two waveforms can be reversed by subtracting
the phase difference from 360 degrees. So, for A and B, with A leading B by
120 degrees we can also say A lags B by 360 - 120 = 240 degrees. And, since
there are 360 degrees in one cycle, if A lags B by 240 degrees and B leads C
by 120 degrees, then A must lag C by 120 degrees. Similar analyses can
be made for systems with other than three phases.
From a strictly theoretical point of view, that's it! We have now have our
complete set of cosine equations for three-phase related sinusoids, which
we can use in terms of angle of rotation as in the three equations above, or in
terms of time via the radial velocity, which, as we have seen, can be expressed
directly, 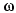 , or in
terms of frequency, f, if we include the proper conversion factor of
, or in
terms of frequency, f, if we include the proper conversion factor of
 .
If we also include an amplitude factor, K, and convert the degree value phase
angles to radian values by multiplying by
.
If we also include an amplitude factor, K, and convert the degree value phase
angles to radian values by multiplying by
 and dividing by 180,
we get a general set of equations we can use to compare three-phase waveforms
of any magnitude and any frequency at any time:
and dividing by 180,
we get a general set of equations we can use to compare three-phase waveforms
of any magnitude and any frequency at any time:
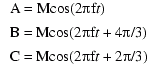
We'll make use of these equations in one from or another later, when we look
at why we make the connections we do between phase coil groups in a polyphase
motor/generator.
Mechanical vs. electrical degrees:
A while back I mentioned we'd look at one more factor to apply to the main
argument in our cosine equations. And, now the time has come. Here we'll step
back a bit from the predominantly theoretical discussions and look at a result
that stems from the basic physical arrangement of magnets and coils in our
motor/generators. This factor is needed to properly define the phase sinusoids
from our cosine equations if we use frequency or radial velocity to mean the
rotational speed of our motor/generator rotor. If we use frequency or radial
velocity to mean the actual cycle rate of our phase sinusoids, then this
factor is not needed in the cosine equations. This discussion assumes we
are relating our cosine equations to rotor revolutions. When we relate our
equations to the actual phase cycle rate, (e.g., 60 Hz for US commercial
electrical power), then the last set of three equations above are the ones we
want to use for a three-phase motor/generator.
While it is true we relate cycles in sinusoids to circular motion, and here,
spinning of the rotor in a motor/generator does ultimately define that
relationship, one rotation of our motor/generator rotor does not equate to one
rotation in our phase sinusoids. In fact, for an AC generator, each turn of the
rotor will result in a number of sinusoidal cycles in the output phase
waveforms. Similarly, a number of input power cycles are required to produce a
single turn of the rotor in an AC motor/generator used in motor mode.
Physical turns of a rotor, as well as cycles of a sinusoidal signal can both be
measured as an angle in degrees or radians. For the moment we'll use degrees.
To differentiate the two motions, we call the angular measure of turns of the
rotor "mechanical degrees," and the angular measure of cycles of the sinusoidal
waveforms "electrical degrees." For a particular motor/generator design, there
is always a fixed ratio between the two.
For the model motor/generator described in the first part of this web page
there are eight sinusoidal phase cycles for each turn of the rotor. Links to
the source code, (you might want to check the comments), and it's outputs, for
a program that computes and plots the electrical degree measure phase waveforms
for this motor/generator are provided below:
![[PolePhase.c]](./thumb/pmg/polephase_c-t.jpg)
![[3-phase waveforms]](./thumb/pmg/phasediag-t.jpg)
![[numeric output]](./thumb/pmg/polephase_data-t.jpg)
Those of you checking my work may have already noticed that the coil count
for the motor/generator I constructed doesn't match the number you would
calculate using the rote formulas presented at the start of this "How's it
work?" section. That difference is due to consideration of a matter known as
cogging, where the drag of magnet fields across the coils affects
motor/generator performance. Don't worry about that, we'll get to it in a
while. For now let's continue the discussion by looking at the
relationship between electrical and mechanical degrees for the eight magnet,
12 coil set we computed earlier for a 3-phase motor/generator using the
rote formulas.
Once again symmetry comes into the picture. Referring back to figure 6, we can
define a mechanical 0 degrees position for the illustrated motor/generator as
the middle of the topmost armature coil, C4. Now say we turn the rotor so that
a north pole magnet aligns with the mechanical 0 position, and define an
electrical 0 position to be where the north pole magnet is aligned with the
mechanical 0 position. Hmmmm...looks like if we turned the rotor to line up
another north pole magnet with the mechanical 0 position, we'd have another
electrical 0 position. That's right! And, that is the answer. The rotor is
radially symmetric, so when we rotate it, we can align it at several positions
and see an identical picture.
In the previous paragraph we defined "a" mechanical 0 degree position and also
"an" electrical 0 degree position. Those nonunique statements, as opposed to
defining "the" mechanical or electrical 0 degree positions, were intentional.
Because of how figure 6 was drawn it is easy to see coil C4 as defining a
mechanical 0 degree position. And, in fact, because of symmetry, the
relationship we are about to investigate could be arrived at using coil C4 to
mark the mechanical 0 degree position. However, because we want to look at what
happens over a full sinusoidal phase cycle when defining the electrical 0
degree position, we will start at the the beginning of a phase coil group,
not because it is at all necessary, but just because it looks better in the
figures. We can start on any phase coil group. Let's choose group A, and define
the mechanical 0 degree position as being marked by coil A1, which, in figure 6,
is just to the right of coil C4.
Again we define the first electrical 0 degree position to be where a north
pole magnet aligns with the mechanical 0 degree position. This is the position
where, when the motor/generator is in operation, the phase A sinusoid will be
at its maximum value. Now, as the rotor turns, there will be multiple
positions where different north pole magnets will pass under coil A1, and all
other coil and magnet alignments will be such that the phase A sinusoid will
reach a maximum. Each time this happens phase A has passed through a full
sinusoidal cycle, and each of these alignments corresponds to a new electrical
0 degree position. The number of full phase cycles per single mechanical
rotation is always in a fixed ratio. That ratio will vary with motor/generator
design, but, we can always see what the ratio is by looking at the relative
alignment, in degrees, between coils and magnets in the design.
We can depict coil/magnet alignment in a linear diagram, similar to how earlier
we diagrammed phase coil connections as linear groups, even though a real
motor/generator armature is circular (e.g., figure 4). In our eight magnet,
12 coil system, there will be 360/8 = 45 degrees between magnets, and 360/12 =
30 degrees between coils. Drawing this arrangement linearly, with one north
pole aligned with coil A1 (figure 20) we can see that the rotor will have to
shift (rotate) 90 degrees to achieve the identical alignment of magnet poles
and coils as seen for the first electrical 0 degrees position.
![[elec. vs. mech. degrees]](./big/pmg/fnfig-20.jpg)
If we see a new electrical 0 degree position for every 90 degrees the rotor
turns then for every turn of the rotor we will see 360/90 = 4 sinusoidal
phase cycles. If you make the same analysis for a ten magnet rotor and use
the rote calculation number of coils, 15, for a 3-phase motor/generator, you
will come up with a ratio of 5 phase cycles per rotor turn. With a little
squinting at the diagrams, the general relationship for the ratio, R, of phase
cycles to rotor turns can be seen to be the result for 360 degrees per phase
cycle being divided by one-half the number of magnets divided into 360 degrees
per rotor turn. That is, if M is the number of magnets:
R = 360/(360/(M/2)).
With a little algebraic manipulation, that becomes:
R = M/2,
which is just the number of pole pairs in the motor/generator. In fact, so long
as the motor is properly designed, the number of coils doesn't enter into the
relationship. For example, we know the coil count for the 16 pole
motor/generator constructed for this web page is not what you would calculate
from the rote formulas. But, we also know the electrical to mechanical degrees
ratio for that motor/generator is 8, and, by our new formula:
R = M/2 = 16/2 = 8.
So, when we use rotation speed of our motor/generator rotor in the main angle
term of our cosine equations, we apply the ratio R = M/2 to that term to
produce the proper number of phase cycles per rotor revolution, giving us
another form for our equations:
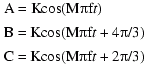
OK, I picked a phase, now what?
So, now we've got some phases spinning around, and described then in fairly
painful detail. What do we do with them? Why, we hook them up to make motors
and generators, of course!
For a single-phase motor/generator, we've already seen that isn't too
difficult. Well, except for that bit about self-starting of single-phase
motors. (Which we'll get to real soon now.) But, it gets a little more tricky
with polyphase motor/generators. There we have multiple electrical signals
going through different strings of coils that have their ends connected
together. Why doesn't it all just short out and burn up? That's where the
rotations, and more importantly the phase angles, come in.
Check this out:
cos(0) = 1.0
cos(240) = -0.5
cos(120) = -0.5
1 + (-0.5) + (-0.5) = 0.
So what? Well, those are the cosine function values for the phase angles
(shown in degrees) for our previous three 3-phase equations. That they sum to
zero is why our three-phase motor/generator doesn't spark and smoke in normal
operation. If you add the same fixed angle to the phase angles in our cosine
equations, the result is always the same. Try it:
cos(875634.43 + 0) = -0.4135812
cos(875634.43 + 240) = 0.9952783
cos(875634.43 + 120) = -0.5816971
-0.4135812 + 0.9952783 + (-0.5816971) = 0.
Try it again if you want to, but I guarantee the result will be the same. What
this means is that no matter what the rotational position of our phase
sinusoids, if we look at them at the relative positions defined by their
phase angles, the electrical waveforms will sum to zero.
Now, by no coincidence, the connection locations for our motor/generator phase
coil groups fall at the relative phase angle positions. So, though the coil
group ends are shorted together, each connection is effectively at zero
voltage, and nothing bad happens. You can see this relationship in, for
example, figure 19. Consider the maximum up excursion of any signal in the
figure to be +1, and the maximum down excursion of any signal in the
figure to be -1. Then, if you sum the observed values for the three sinusoids
at the same position along the horizontal axis, you will find the result is
always zero. This relationship will hold whether we are considering the
rotation in degrees, frequency, or time. So long as we observe the correct
phase difference, the sum is always zero. And, of course, this extends to
numbers of phases other than three.
It might seem that connecting a motor/generator so that the voltages at its
phase wires sum to zero won't accomplish much. But, these are relative
voltages. If you look across the phase coil groups instead of just at each
of the ends, you will see a voltage difference. This is why though the
connection voltages sum to zero, you should not go probing them with a wet
finger! (Or a dry one, for that matter.)
The across phase-coil-group voltage difference relationship can also be seen
in figure 19. Look at the difference in voltage for each sinusoid over their
specified 120 degree phase difference locations. That is, from 0 to 120
degrees for phase A, from 120 to 240 degrees for phase B, and from 240 to 360
degrees for phase C. In each case we see a difference of 1.5 (as a change
from +1 to -0.5). The total excursion for each sinusoid is 2.0 (as a change
from +1 to -1), so we see across each phase 0.75 of the total excursion.
There are specific mathematical relationships for the continuous values of
the phase voltage differences over time. They are often expressed in terms
of rotating vectors. We'll look at those as we investigate the primary types
of phase connection configurations.
You say delta, I say why?
Phasors don't have to stun:
Before we get on with looking at some of the possible motor/generator phase
wiring configurations, first lets take a look at a some notation to use
for our rotating phases. For the most part, we aren't going to be concerned
with the absolute angles of rotation of our phases, but just with their
relative phase angles, and their magnitudes (which may be looked at in terms
of either current or voltage). We know we are talking about sinusoids all of
the same frequency here, so, rather than using the cosine equations to formally
state that, we can just use a notation that gives us the magnitudes and phase
angles we need. Here's one:
K
The parameter K is the magnitude of the sinusoid, and the parameter nnn gives
the phase angle of the sinusoid relative to the zero phase angle sinusoid.
The phase angle parameter could be given in any units, but, here, as
indicated, we'll use degrees. So, you can read the notation as "K at an angle of
nnn degrees."
This notation may look familiar. If you've done any AC circuit analysis it
probably should. It is traditional phasor notation as derived from the complex
exponential representation of a sinusoid. We aren't going to worry too much
about its derivation here. Mainly we're just going to concern ourselves with
how to add phasors together to see if our motor/generator designs fit the
criterion we established in the last section, that the physical connection
points for our phase coil groups are made where their phase waveforms will
sum to zero. For our purposes, often that will amount to just adding
the phase angle values to see if they sum to zero, where 0 in degrees is
defined as some integer multiple of 360 degrees. For example, ignoring
the parameter K, (that is, call it equal to 1), we can sum the phasor
equivalents of our three-phase cosine equations as:
 +
+
 +
+
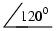 =
=
 =
=
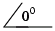
That is, our 3 three-phase phase-angles sum to zero. And, that summing to zero
is the condition we want, regardless of the number of phases we are working with.
Phase arrangements:
This section is brought to you by the letter Y. Why do people have to do
all those the weird phonetic things they do when they want to express the
25th letter of the English alphabet, Y? I'm dyslexic. I have a hard enough
time getting letters sorted out using a spell-checker, and all those things
involving "w" and "e" people do when they want to say "y" just make my head
want to explode. So, here, when we talk about "delta" systems, we'll call them
delta systems, and when we talk about "Y" systems we'll call them Y systems.
There are a lot of different ways to arrange the wiring of a polyphase
motor/generator. But, they center around the two basic configurations, the
delta and the Y. In fact, most of the alternative configurations are just
combinations of delta and Y circuit arrangements.
Most of what we talked about so far has been while referring to delta wired
motor/generators. But, the discussion also applies to Y configured systems.
The same phase coil group "head-to-tail" wiring method described in the rote
instruction sections holds for delta and Y arrangements, as does the notion
of phase voltages summing to zero at the phase group connection points.
What mainly differentiates delta and Y systems is the connection of their
phase coil groups. We've seen the delta connection before (figure 5), so,
let's take a look at the Y connection. For our ongoing case of eight magnets
and 12 coils, we would connect our phase coil groups the same as we did for
our delta wired motor/generator (figure 4), but, rather than connect the
phase coil groups in "head-to-tail" fashion, we connect them "head-to-head."
That is, if we consider the positive lead of a phase coil group to be the
"tail" of the first current arrow as drawn its coil connection diagram, and
the negative pole to be the "head" of the last current arrow in its coil
connection diagram, then we connect the negative leads. For a three-phase
motor/generator, this gives us a three-armed or "Y" configured circuit, where
the free ends are our A,B,C phase input/output leads (figure 21).
![[Y configuration]](./big/pmg/fnfig-21.jpg)
Unless you look close at the wiring, the basic physical design we've seen for
a delta wired motor/generator (figure 6) looks the same for a Y configured
motor/generator (figure 22).
![[Y motor/generator]](./big/pmg/fnfig-22.jpg)
So, what about that connection voltages summing to zero thing? Does that still
hold for the Y configuration? Yep. Take a look. Consider driving the Y as
a motor. The free ends are provided with the phase inputs, which we already
know sum to zero due to their phase differences. Since the phase group coils
are identical, and we've connected them so that phase currents flow without
interfering with themselves, the voltages seen on the other ends of the
phase coil groups will not change phase, and, hence, still sum to zero at the
Y connection point. Symmetry dictates the same holds true when using the system
as a generator. The same sinusoidal phase relationship diagrams we developed
when discussing the delta wired motor/generator also hold for the Y system.
Before we get into considerations of power and efficiency that might affect
one's choice of a delta or a Y configuration, there is one significant
difference to note between the two connection styles. The Y connection
allows including a neutral line along with the phase lines if we choose to.
By connecting a lead to the phase coil group junction we get a three-phase
4-wire connection, while without the additional lead the connection is known
as a three-phase 3-wire connection (figure 23).
![[Y 3 and 4 wire connections]](./big/pmg/fnfig-23.jpg)
There are a number of reasons to choose to include or not include a neutral
line in a polyphase AC system. Mainly they relate to safety and power
balancing considerations, and are not terribly relevant to the discussion at
hand. So, we won't cover the issue of neutral lines more in this section, or
in any great detail later.
One thing that is somewhat relevant to our current discussion is the matter
of power and efficiency for the delta versus a Y connected motor/generator.
Way back near the beginning of all this I said something about the delta
being more efficient at lower rpms and that is why it was chosen as the
configuration for the initial polyphase rote design instructions. Some of
you may disagree with that, if you know that for a given rpm the Y produces
a a higher voltage than the delta. Well, efficiency is in the eye of the
beholder. For a given rpm the delta produces more current than the Y,
and, me, I'm looking for maximum current, not maximum voltage, so the delta
makes more sense for my purposes. But, lets take a closer look and see
about how to figure out if it makes sense for your application on not.
Note that outside the standard electrical current and voltage relationships
which hold anywhere, the discussion that follows will refer to three-phase
systems only.
Whether we are looking at a delta or a Y system, there are two voltages to
consider, coil voltage and line voltage. Coil voltage is the voltage read
across any coil, where "coil" means the entire phase coil group when there
is more than one coil per phase coil group. A motor/generator's A,B,C, phase
leads are commonly referred to as the "lines" and line voltage is the voltage
read between any pair of lines (figure 24).
![[coil and line voltages]](./big/pmg/fnfig-24.jpg)
The following relationships hold for coil and line voltages and currents
in a three-phase delta system:
Coil Voltage = Line Voltage
 * Coil Current =
Line Current
* Coil Current =
Line Current
The following relationships hold for coil and line voltages and currents
in a three phase Y system:
 * Coil Voltage = Line Voltage
* Coil Voltage = Line Voltage
Coil Current = Line Current
Given those relationships, and the rule of thumb that the line resistance,
(i.e., the resistance measured between any two lines), in a Y system is
typically about 3 times the line resistance in a delta system, we can make a
few calculations and look at differences in output from the two.
If we measure the voltage and current in one phase of a generator, (where here
phase means one phase coil group, or the "coil" as described in a previous
paragraph), independent of the other phases, we can use those readings to
calculate what the line voltage and current will be for the generator
connected in either a Y or a delta configuration.
Say in one phase of a generator we see 28 volts and 10 amps. Then, using the above
relationships, wired as a delta the generator would have the same line voltage, 28
volts (V), and a line current of
 * 10 = 17.3 amps
(A). Rewired as a Y, the same generator would have a line voltage of
* 10 = 17.3 amps
(A). Rewired as a Y, the same generator would have a line voltage of
 * 28 = 48.5 V, and
a line current of 10 A.
* 28 = 48.5 V, and
a line current of 10 A.
Now, the power in an electrical circuit in watts (W) is equal to the voltage
in volts times the current in amps, So from any two lines in our Y
configured generator we get 48.5 V * 10 A = 485 W, and, similarly, as a delta
we see 28 V * 17.3 A = 484 W for any two lines.
Hmmmm, 485 W versus 484 W, that doesn't seem too significant a difference.
And, it isn't. The power out of a generator is related to the power you put
into spinning it. Whether we wire it as a delta or a Y, if we spin our
generator so in either case we get the same phase measurements, then we are
basically putting the same amount of power into it. So, in that case, we
really can't get any more power out of one configuration over the other.
OK, then why choose one over the other? It comes down what you are trying to
do, and how fast you can spin.
Say we made our above measurements at 400 rpm. For the delta that means
400 / 28 = 14.3 rpm per volt, and for the Y we have 400 / 48.5 = 8.2 rpm
per volt. If we reved up to 1000 rpm, from the delta we would see around
1000 / 14.3 = 69.9 V, and from the Y we would see around 1000 / 8.2 = 122 V.
Now, rather than choose an arbitrarily coil current, lets use the
convenient, but not unrealistic line resistances of 3 ohms for a Y system,
and 1 ohm for a delta system and see what we get for power while we are
charging a battery.
Lets cheat a little bit and ignore the need for rectifying the output
alternating current (AC) voltage to a direct current (DC) voltage before
applying it to the terminals of a battery for charging. As far as the two
types of voltages are concerned, rectification results in a known, fixed
multiplication factor being applied to the AC voltage level to obtain the
DC voltage level, so the calculations that follow are valid, but just
missing a multiplier. We'll get to rectification in a later section.
The voltage (V) across a circuit is equal to the current (I) through the
circuit times the resistance (R) of the circuit, that is, V = I * R. We
can manipulate that equation any way we like, and, hence, I = V / R, which
we use with our generator line voltage and resistance to calculate the
line currents. Actually, to calculate the generator line currents in the
case of charging a battery, we subtract the battery voltage from the
previously calculated generator line voltages because the battery is
compensating for part of the measured line voltage. So, for a nominal 12.5
battery level charged by the Y configured generator spinning at 1000
rpm we have 122 - 12.5 = 109.5 effective line voltage, which, with the
line resistance of 3 ohms gives us 109.5 V / 3 ohm = 36.5 A line current.
Similarly, for the delta we have (69.9 - 12.5) V / 1 ohm = 57.4 A line
current.
A battery being charged by a generator is essentially a series circuit,
and the current through a series circuit doesn't change. (We'll talk more
about series and parallel circuits later.) So, for comparison of the Y and delta
generator configurations, we can look at the power output relative to the
nominal battery voltage because we see the same current no matter
where we look in the circuit, and it will give us an idea of how much
power we have available to charge the battery. That is for the Y we see
36.5 A * 12.5 V = 456 W, while for the delta we see 57.4 A * 12.5 V = 718 W,
or 253 W more power available for charging from the delta than the Y when
both are spinning at 1000 rpm.
That more output power is available from the delta at a given rpm is
an advantage so long as we have the input power available to spin it
fast enough to get the required output voltage. If we are constrained
by input power, and hence to lower rpm, then the Y configuration can
be an advantage when, say, charging a battery. To get the minimum required
approximately 13.5 V for charging a standard lead-acid battery, our
example delta generator would need to spin 13.5 V * 14.3 rpm per volt = 193
rpm, while the Y would require 13.5 V * 8.2 rpm per volt = 111 rpm. So,
though we would not be producing as much power as when spinning at 1000 rpm
and hence would not be able to charge a battery as fast, we might still be
able to charge a battery with the Y configured generator when we could not
with the delta generator due to rpm constraints.
Some motor/generators take advantage of the voltage and current relationship
difference between delta and Y configurations and start in the Y configuration
to take advantage of higher voltage and lower current at low rpm, and then
switch themselves to a delta configuration once the line current is sufficient
to energize a coil that creates a magnetic field strong enough to pull in a
spring loaded switch that makes the configuration change. (That's one way,
anyway, there are other methods.) So long as the rpm stay high enough to
maintain the required voltage level, the motor/generator runs in the the delta
configuration and takes advantage of the higher available current. Otherwise
the system drops back into the Y mode and maintains the required voltage level
at the lower rpm.
Rollin' Rollin' Rollin'
Well, rotatin' rotatin' rotatin' more precisely. Rotating magnetic fields,
that is. Which are at the heart of all we've been talking about. The notion
of rotation we covered a lot already with our sinusoids and their multiple
forms of cosine equation descriptions. Plus, "moving" magnetic fields have
been mentioned before, too. It's pretty clear that the magnetic fields of
magnets mounted on a spinning rotor must be rotating, since their magnets
are rotating. (Of course, there a few more details to fill in there.) And,
what about those magnetic fields created from our nonspinning armature coils
when we apply phase input power? Well, they are rotating, too!
In the last section we talked a lot in terms of generators. Here, we'll cover
things for the most part in terms of motors. Everything in this and the last
section pretty much applies to motors or generators, (remember symmetry), but,
the phenomena are just easier to visualize as described. The key thing to
note is, like the term "phase," the term "rotation" can have somewhat
different meanings depending on context.
Moving? Rotating?
Moving a magnet obviously moves its magnetic field along with it. So, rotate
a magnet, and its magnetic field rotates, too. OK. That's a straight forward
concept. But, let's look just a little bit closer.
First, we'll consider the magnetic field of a single magnet. Note that all
magnets are dipoles, that is, they have two components (north and south
poles), that are inseparable. There are a number of formulae that can come
into play when looking at dipole magnetic fields. We don't need to worry
about them too much here, and just note that the strength of a magnetic field
near a dipole falls off as
1/ , where r
is the distance from the center of the dipole. (This is different than the fall
off from a monopole, such as a positive or negative electric charge, where
field strength falls off as
1/
, where r
is the distance from the center of the dipole. (This is different than the fall
off from a monopole, such as a positive or negative electric charge, where
field strength falls off as
1/ .)
.)
The 1/ relationship (figure 25) applies best on the molecular scale, but
for a passable approximation it will work to look at field strength from, for
example, one of the neodymium discs on the model 3-phase motor/generator
rotor constructed for this web page.
relationship (figure 25) applies best on the molecular scale, but
for a passable approximation it will work to look at field strength from, for
example, one of the neodymium discs on the model 3-phase motor/generator
rotor constructed for this web page.
![[1/(r**3)]](./big/pmg/fnfig-25.jpg)
If we ignore the mathematical artifact where the field blows up to infinity at
a distance of r = 0, and kind of fudge over the fact that our disc has a
significant diameter relative to a molecule by smearing out the field over
the width of the disc and plotting the field change relative to the edge of
the disc, we get something that gives some idea of the field strength near
the disc. The take home message here isn't the exact form of the field, but
that field strength falls off fairly rapidly away from the disc, and we are
left with essentially a magnetic field "bump" above our magnet. (figure 26).
![[magnetic 'bumps']](./big/pmg/fnfig-26.jpg)
Now, consider the magnets on the spinning rotor of our basic design
motor/generator. What we have is a series of intense magnetic bumps, with
alternating poles, evenly spaced around the perimeter of the rotor. Assuming
the gap between the moving rotor magnets and the stationary armature coils
is small enough (we'll talk a bit about proper gap width later), then the
"bumps" will move through the armature coils, creating a current in the coils.
If we didn't have the magnetic bumps, but rather a uniform field around the
rotor, then even though the rotor was spinning, and the field effectively
moving, the coils would not see much if any change in magnetic field, and,
hence, produce little to no current. It isn't just that a magnetic field is
moving that causes current flow in a wire, but that the field intensity is
changing, and the moving magnetic bumps give that necessary
intensity change.
For our alternating pole rotor, we not only see relative level changes in
field intensity as the rotor spins, (i.e., a changing magnetic field), but we
also see full alternating pole magnetic field changes. This alternating of
poles, as discussed before, causes reversal of (alternating) current in our
armature coils. Voila, AC generator!
In the case of using the motor/generator in motor mode, you can consider the
magnetic "bumps" along the edge of our permanent magnet rimmed rotor to be the
equivalent of teeth on a gear. But, then, what is pushing these "teeth" to
make our motor rotor spin? The answer is the rotating magnetic field produced
by our armature coils when we apply power to its phase coils.
Inducing synchronization:
The brushless permanent magnet motor is what is referred to as a synchronous
motor. That means its rotor spins at synchronous speed, where synchronous
speed is an rpm value that is a direct function of the input phase line
frequency and the number of armature poles in the motor.
Under normal use conditions there is no slip of the rotor in a synchronous
motor relative to the rotating magnetic field created by the phase line power
input to its armature coils. This is as opposed to an induction motor, where
there must be some slip of the rotor (i.e., its speed less) relative to the
rotating armature field so that currents are induced in conductors embedded in
the rotor which in turn create magnetic fields that act as the magnetic fields
produced by the permanent magnets on the rotor of our brushless permanent
magnet motor. The synchronous type motor makes a good motor/generator. The
induction motor is not quite so well suited to acting also as a generator.
Now, electrical current moving through a wire travels basically at the speed
of light, which is about 1 foot per nanosecond (0.000000001 second). And, since
we are talking about input power frequencies generally of less than 100 Hz,
(giving a cycle period on the order of 0.01 second), with total wire lengths on
the order of tens to hundreds of feet, for all intents and purposes, every coil
in a phase coil group sees the same power level at the same time, tracking the
input power level as it arrives at the phase line input. So, if everything seems
to happen at once, how do we produce anything like a rotating magnetic field
from our stationary armature coils? Well, there are a few aspects to that, in
particular, the alternating polarity wiring of the armature coils which produces
opposite pole magnetic fields in adjacent coils as current flows through them,
and also, in the case of polyphase systems, the phase difference between the
phase line inputs which produces a lead or lag between magnetic fields
produced in different phase coil groups.
Probably the most commonly seen formula for synchronous speed is:
S = 120f/p
where: S = synchronous speed in rpm (revolutions per minute)
f = input phase line frequency in Hz (cycles per second)
p = number of armature poles (coils).
Let's stare at that just a tad and see if we can figure out what's going on.
Since we are using frequency, f, in Hz, or cycles per second, and S comes out
in rpm (revolutions per minute) there must be a factor of 60 seconds per minute
in there, so, we could rewrite the formula for S as:
S = (2)(60)f/p.
Now, if we wanted to convert from, S, speed in rpm to, say, N, speed in rps
(revolutions per second), all we have to do is toss out the factor of 60
seconds per minute, leaving us with:
N = 2f/p.
Apply a little algebra, and we get:
N = f/(p/2).
That is, synchronous speed in revolutions per second is equal to the input phase
line frequency in Hz divided by one-half the number of armature poles. That is to
say, synchronous speed in revolutions per second is equal to the input phase
line frequency in Hz divided by the number of armature pole pairs.
OK, there's that "pole pair" thing again. So, where's it come from? Well, it
comes from the same place it did when we were looking at mechanical vs.
electrical degrees a while back. There we had a sequence of alternating pole
permanent magnets. Here, due to the armature phase coil group wiring
technique, we have alternating pole electromagnets. In either case, to see the
the same action at a pole we have to look at every other pole. That is one
half the poles give a different action, and one half the poles is also the
number of pole pairs. Hence, the number of pole pairs becomes an important
factor in the calculations. In fact, in a while we'll take a look at a diagram
very similar to the one we looked at when discussing electrical vs. mechanical
degrees (figure 20) as we further define the concept of synchronous speed. But,
first, let's just take a closer look at the concept of an actual rotating magnetic
field.
It is actually easier to conceptualize a rotating magnetic field when examining
the properties of a polyphase motor than it is when considering a single phase
motor. In fact, a self-starting single phase motor is, at least on startup,
connected so that it actually runs as a two phase motor. (More on that to come.)
In general, to establish a rotating magnetic field the number of armature
poles (coils) must be equal to, or a multiple of, the number of input power
phases, with the poles being separated by the phase angle between the input
power phases.
As pointed out earlier, the number of armature poles and the number of rotor
pole (magnet) pairs are related. That is, for each rotor magnet pair must be a
set of armature coils equal in number to the number of input power phases. Note
how this relationship, by default, meets the criterion given above for the
number of armature poles required to establish a rotating magnetic field.
So, we know how many armature coils we need to set up a rotating magnetic
field, and that our properly designed motor/generator will have that number
of armature coils. Let's finally take a look at how all this sinusoidal
signal, spinning vector, rotating field stuff comes together. We can look a
simple case, say a two pole-pair, three phase, delta configured motor. Now,
another diagram is in order. For that we can use a new form of the armature
coil connection diagram we've seen before, same as our original linear diagrams,
(e.g., figure 5), just wrapped in a circle to represent a more realistic
motor/generator armature. For our two pole-pair, three phase motor/generator we
will end up with a circular figure having six armature coils representing two
three-coil phase groups (figure 27).
![[6 pole armature]](./big/pmg/fnfig-27.jpg)
Using figure 19 as a reference for the phase relationships of three-phase
sinusoidal currents, let's examine the magnetic fields that would be generated
in the coils of figure 27 by application of three-phase power. Consider that
a positive current through a coil wired as is coil A1 relative to its input
phase power will produce a north magnetic pole pointing inwards towards the
center of the ring of armature coils.
We've seen that we can look at our sinusoidal signals in terms of degrees or time
and get the same results. So, take time zero,
 , to be the zero
degree position for phase A, take time two,
, to be the zero
degree position for phase A, take time two,
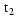 , to be the zero
for phase B, (120 degrees for phase A), and take time four,
, to be the zero
for phase B, (120 degrees for phase A), and take time four,
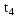 , to be the zero
degree position for phase B, (240 degrees for phase A). Note, relative to the
waveforms in figure 19, this means at time
, to be the zero
degree position for phase B, (240 degrees for phase A). Note, relative to the
waveforms in figure 19, this means at time
 phase A is at a
positive maximum, at time
phase A is at a
positive maximum, at time
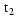 phase B is at a
positive maximum, and at time
phase B is at a
positive maximum, and at time
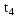 phase C is at a
positive maximum. But, let's concentrate just on phase A for a moment.
phase C is at a
positive maximum. But, let's concentrate just on phase A for a moment.
Note while coil A1 produces a maximum strength north pole oriented towards
the center of the armature ring at
 , coil A2, being
wired for the opposite polarity, produces a maximum strength south pole oriented
towards the center of the armature ring. The physical arrangement of coils in
figure 27 puts A1 and A2 opposite each other on the armature ring, which means
at time
, coil A2, being
wired for the opposite polarity, produces a maximum strength south pole oriented
towards the center of the armature ring. The physical arrangement of coils in
figure 27 puts A1 and A2 opposite each other on the armature ring, which means
at time  there is
the maximum possible magnetic field strength between coils A1 and A2. Also note
that at the 90 degree position for phase A, or three quarters of the time between
there is
the maximum possible magnetic field strength between coils A1 and A2. Also note
that at the 90 degree position for phase A, or three quarters of the time between
 and
and
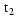 , the A phase value
drops to zero, and at that time there is no phase A current generated magnetic
field between coils A1 and A2.
, the A phase value
drops to zero, and at that time there is no phase A current generated magnetic
field between coils A1 and A2.
Of course, there are two other input phases, and, as we already know, none of
the three are always at their maximum value. Again referring to figure 19, we
can see that at time
 , when phase A is
at its positive maximum value, both input phases B and C are are at one half
their maximum negative value. Similarly, at time
, when phase A is
at its positive maximum value, both input phases B and C are are at one half
their maximum negative value. Similarly, at time
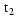 , phase B is at its
positive maximum while phases A and C are at one half their maximum negative
value. And, at time
, phase B is at its
positive maximum while phases A and C are at one half their maximum negative
value. And, at time
 phase C is at its
positive maximum with phases A and B at one half their negative maximum. For now
let's just concentrate on time
phase C is at its
positive maximum with phases A and B at one half their negative maximum. For now
let's just concentrate on time
 .
.
We have already established that at time
 the magnetic field
between coils A1 and A2 is at its maximum, and oriented north to south from A1
to A2. For phase B at
the magnetic field
between coils A1 and A2 is at its maximum, and oriented north to south from A1
to A2. For phase B at
 , recall the rote
coil connection scheme dictates that coil B2 is the phase input coil and thus
wired so that a positive current generates a magnetic field with its north poll
oriented towards the center of the armature ring while coil B1 is wired so a
positive current generates a magnetic field with its south pole oriented towards
the center of the armature ring. So, with the B phase being negative at
, recall the rote
coil connection scheme dictates that coil B2 is the phase input coil and thus
wired so that a positive current generates a magnetic field with its north poll
oriented towards the center of the armature ring while coil B1 is wired so a
positive current generates a magnetic field with its south pole oriented towards
the center of the armature ring. So, with the B phase being negative at
 , coil B2 generates
a magnetic field with its south pole oriented towards the center of the armature
ring and coil B1 generates a magnetic field with its north pole oriented towards
the center of the armature ring, and develops a total field strength around one
half that of the field between coils A1 and A2. Similarly, the total field
between coils C1 and C2 is approximately one half the field between coils A1 and
A2, oriented north pole to south pole from coil C2 to coil C1. Well, at least
that is what would happen if the different phase fields didn't interact. In
reality, the full strength field extends between coils A1 and A2 as described,
but, the weaker north pole field from C2 is deflected by the stronger north pole
field from coil A1 and connects to the weaker south pole field from coil B2,
while the weaker north pole field from coil B1 is deflected by the field from
coil A1 and connects to the weaker south pole field from coil C1. In a
simplified form, the arrangement of flux lines in the armature ring at time
, coil B2 generates
a magnetic field with its south pole oriented towards the center of the armature
ring and coil B1 generates a magnetic field with its north pole oriented towards
the center of the armature ring, and develops a total field strength around one
half that of the field between coils A1 and A2. Similarly, the total field
between coils C1 and C2 is approximately one half the field between coils A1 and
A2, oriented north pole to south pole from coil C2 to coil C1. Well, at least
that is what would happen if the different phase fields didn't interact. In
reality, the full strength field extends between coils A1 and A2 as described,
but, the weaker north pole field from C2 is deflected by the stronger north pole
field from coil A1 and connects to the weaker south pole field from coil B2,
while the weaker north pole field from coil B1 is deflected by the field from
coil A1 and connects to the weaker south pole field from coil C1. In a
simplified form, the arrangement of flux lines in the armature ring at time
 looks like the
depiction in figure 28.
looks like the
depiction in figure 28.
![[6 pole armature]](./big/pmg/fnfig-28.jpg)
We could go on producing diagrams similar to figure 28 to show the orientation
of magnetic flux lines in the armature ring at times other than
 . But, that would
get very tedious very fast. Instead, we'll switch to phasors and rotating
vectors to simplify things.
. But, that would
get very tedious very fast. Instead, we'll switch to phasors and rotating
vectors to simplify things.
Getting into the spin:
A few sections back we introduced basic phasor notation. There we saw how it
describes a vector by giving the vector's magnitude and direction. Lets dig
into it a bit deeper and look at how it can represent spinning vectors.
Phasor notation gives the direction for a vector as an angle relative to
a fixed starting point, the tail end of the vector. Since one end of the
vector is fixed in place, if we change the direction angle, the vector will
pivot around the fixed end point until it aligns with the new direction
angle. And, if we change the angle value continuously in one direction
the vector will spin around its fixed end point (figure 29).
![[angle change rotation]](./big/pmg/fnfig-29.jpg)
OK, it's clear that phasor notation can represent a rotation. But, how to make
that rotation represent our motor/generator phases? Well, all we need do is
force the angle argument to change in time with the same cycle rate as the
motor/generator input phases. And, it's radians to the rescue! (Again.) Just
using the same angle arguments we previously developed for our cosine
equations as the angle argument in the phasor notation vector representation
gives us vectors spinning with the same cycle rate (frequency) and phase
differences as our motor/generator input phases.
If we view the rotating vectors (phasors) as something akin to the simple
machine presented in figures 15 and 16 for converting circular to linear motion,
then the relationships for the phasor magnitudes can be deduced. Since our
input phases are identical except for their phase differences we need look
at just one of them to determine the magnitude relationships for all. (That
relationship is, of course, to scale the maximum magnitude by the cosine
function. But, for the sake of drawing some more pretty pictures, let's soldier
on a while longer.)
Looking carefully at how the our conversion machine works, in figure 15 we can
see that the position of the peg on the disc determines the amplitude of the
waveform the machine produces. At any time in a revolution of the disc, regardless
of the angle of the peg relative to the machine's axle shaft, the perpendicular
distance of the peg from a horizontal line drawn through the center of the axle is
equal to the amplitude of waveform traced by the pencil attached to the end of the
shaft moved by the peg.
If we think of the peg in our machine's disc as marking the head of a rotating
vector (phasor) and the axle shaft as marking the fixed tail point of that vector,
then we can also think of the perpendicular height of the tip of our rotating
vector relative to a horizontal line drawn through its fixed tail end point as
defining the amplitude of the waveform drawn by our machine (figure 30).
![[phasor vs. machine]s](./big/pmg/fnfig-30.jpg)
Clicking on the thumbnail below will launch an animation demonstrating the
change in amplitude with phasor rotation. The animation cycles 25 times. If
you haven't gotten bored with it before then and already hit the back button
in your browser to return to this text, then you can hit your browser's reload
button to run the animation again, until you do get bored.
![[rotating vector]](./gifs/pmg/Phasor-t.jpg)
We have established that our machine drawn waveform describes a sinusoid, so,
our rotating vector also describes the same sinusoid. This means our rotating
vector (phasor) sinusoid can be used to define our motor/generator phase input
sinusoids, just as we have already done using the cosine functions that
describe the waveforms produced by our circular-to-linear motion conversion
machine. We have also shown how to graphically produce the proper magnitude for
our phasors. But, we aren't quite done yet. We need to apply both the direction
and magnitude simultaneously to properly illustrate the phasor in action.
By definition, a vector, rotating or not, describes a length (magnitude) and
the direction to point that length towards. To complete our picture, we need
to not just project the magnitude from tip of the vector onto a line as done
in the previous figures, but, take the projected magnitude values and align
them in the direction of the vector at the time they were generated.
Considering again just phase-A, with no phase angle, and clockwise rotation.
The phasor starts out with its positive maximum magnitude directed vertically up
at an angle of 0 degrees. The only other maximum is negative occuring when the
vector is again vertical, only directed down at an angle of 180 degrees.
At 90 degrees and 270 degrees the magnitude is 0. The effect is in one cycle
for the phasor to scribe a figure-eight shaped path around its fixed tail
point (figure 31).
![[figure-eight]](./big/pmg/fnfig-31.jpg)
Clicking the thumbnail below brings up an animation that illustrates the
change in magnitude with rotation describing a figure-eight shaped path.
![[figure-eight phasor]](./gifs/pmg/Mag-t.jpg)
Now, don't be fooled. The phasor described above isn't really our long sought
after rotating magnetic field. The phasor, in this case, simply describes the
change over time in the magnetic field relative to the phase A coils, A1 and
A2. Between coils A1 and A2 the magnitude of the magnetic field generated due
to the phase A input increases and decreases, as well as changes its polarity
when the input current changes polarity, but, in and of itself, it doesn't rotate.
The rotation indicated in the figures and animations above is just really a
way of illustrating the change over time. None the less, the "figure-eight"
magnitude change is the key to the rotating magnetic field.
We noted in describing the magnetic flux diagram of figure 28 that, because
of the way the phase coil groups are wired, at time
 the fields from
each group are directed towards the center of the armature coil with the same
magnetic polarity, north to south, but have different magnitudes, with the
strongest flux associated with the phase A coil group. No matter at what time in
an input phase cycle we look, the flux across each coil group will always have
the same polarity, though all polarities may be reversed and which phase coil
group is exhibiting the maximum flux will change. It is this shift in flux
magnitude between the phase coil groups which leads to a rotating magnetic
field due to the polyphase input signals.
the fields from
each group are directed towards the center of the armature coil with the same
magnetic polarity, north to south, but have different magnitudes, with the
strongest flux associated with the phase A coil group. No matter at what time in
an input phase cycle we look, the flux across each coil group will always have
the same polarity, though all polarities may be reversed and which phase coil
group is exhibiting the maximum flux will change. It is this shift in flux
magnitude between the phase coil groups which leads to a rotating magnetic
field due to the polyphase input signals.
For our three-phase system we have three rotating phasors, each leading the
next by a phase angle of 120 degrees. If we plot the figure-eight magnitude
changes for each phasor on the same diagram, the result provides more insight
into the nature of the rotating magnetic field. From such a diagram (figure
32) we can see loops in the magnitude change plots for the individual phasors
intersect at the center of the figure, but each fills the gap between its
adjacent phase loops, with some overlap. As explained in the text of figure 32
this figure can be used to determine the magnitude and direction of the
phase coil magnetic fields in our 3-phase motor/generator.
![[3-phase figure-eights]](./big/pmg/fnfig-32.jpg)
Still, we haven't quite got to the real deal rotating magnetic field. The
animation which can be viewed by clicking the thumbnail below may help shed
some light the matter. It shows the figure-eight sweeping magnitude for
all three phases, in their proper orientations, at the same time.
![[triple phasor]](./gifs/pmg/3Mag-t.jpg)
Again, recognize that in the above figures and animations we are not looking
at rotations in the sense of a magnetic field moving around the armature ring.
What we are looking at is the change over time of the flux associated with
each phase coil group. The apparent rotation in the figures is just a way of
representing the repeating cycle of the changes. It is the combination of
the changes in all phases at once that produces the rotating magnetic field.
It all adds up:
OK. We have our rotating vectors, also called phasors, spinning in sync with
our phase inputs, and having magnitudes representing the current flows through
our phase coil groups which are proportional to the magnetic field fluxes from
the armature phase coils. Also, a while back, we noted at time
 (figure 28)
that because of how the phase coil groups are wired the polarity of the magnetic
fields from each group is oriented in the same direction towards the center of
the armature ring. Again referring to figure 19, let's call the negative
maximum for phase C time t1, the negative maximum for phase A time t3, and the
negative maximum for phase B time t5. Similarly to how we did for time
(figure 28)
that because of how the phase coil groups are wired the polarity of the magnetic
fields from each group is oriented in the same direction towards the center of
the armature ring. Again referring to figure 19, let's call the negative
maximum for phase C time t1, the negative maximum for phase A time t3, and the
negative maximum for phase B time t5. Similarly to how we did for time
 to produce figure 28,
we can take a look at the fluxes for the phase coils at time
to produce figure 28,
we can take a look at the fluxes for the phase coils at time
 . Except this time
instead of producing another picture like figure 28 we'll use vectors to make our
graphic representation.
. Except this time
instead of producing another picture like figure 28 we'll use vectors to make our
graphic representation.
At time
 , the picture is
simply the reverse of the picture at time
, the picture is
simply the reverse of the picture at time
 . The
magnitudes of phases B and C are one half the magnitude of phase A, with phase
A current flow negative and phases B and C current flow positive. As we saw when
discussing figure 28, due to the wiring of the phase coil groups polarities of
the magnetic fields for all groups are oriented in the same direction towards
the center of the armature ring, but this time instead of north to south from
coil A1 to A2, it is south to north from coil A1 to A2, with weaker south to
north fields from coil B1 to C1 and from coil C2 to B2. To be consistent, from
here on we will always talk of our magnetic fields in terms of flux from north
to south. So, at time t3 we will say our fields are north to south from coils
A2 to A1, C1 to B1, and B2 to C2.
. The
magnitudes of phases B and C are one half the magnitude of phase A, with phase
A current flow negative and phases B and C current flow positive. As we saw when
discussing figure 28, due to the wiring of the phase coil groups polarities of
the magnetic fields for all groups are oriented in the same direction towards
the center of the armature ring, but this time instead of north to south from
coil A1 to A2, it is south to north from coil A1 to A2, with weaker south to
north fields from coil B1 to C1 and from coil C2 to B2. To be consistent, from
here on we will always talk of our magnetic fields in terms of flux from north
to south. So, at time t3 we will say our fields are north to south from coils
A2 to A1, C1 to B1, and B2 to C2.
Now, how do we represent the situation at time
 or
or
 with vectors?
Pretty straight forward. We know the lengths of our vectors represent magnitude,
so, at time
with vectors?
Pretty straight forward. We know the lengths of our vectors represent magnitude,
so, at time
 or
or
 the phase A vector
will be twice the length of the phase B and C vectors. Further, we know
the orientation and wiring of our phase coils, so we can determine the polarity
of our phase coil magnetic fields and hence the direction to draw our vector
arrow heads. This means at time
the phase A vector
will be twice the length of the phase B and C vectors. Further, we know
the orientation and wiring of our phase coils, so we can determine the polarity
of our phase coil magnetic fields and hence the direction to draw our vector
arrow heads. This means at time
 , from the position
of coil A1 on our armature ring we draw a full length vector representing the
phase A magnetic flux to coil A2, and, from the same starting point two half
length vectors, one at 60 degrees from the right of the full length vector and
the other at 60 degrees from the left of the full length vector. Examining
figure 28, we can see that the half length vector pointing 60 degrees to the
right represents the B phase north to south contribution to the picture (coils B1
to C1) and the half length vector pointing 60 degrees to the left represents the
C phase north to south contribution (figure 33A). At time
, from the position
of coil A1 on our armature ring we draw a full length vector representing the
phase A magnetic flux to coil A2, and, from the same starting point two half
length vectors, one at 60 degrees from the right of the full length vector and
the other at 60 degrees from the left of the full length vector. Examining
figure 28, we can see that the half length vector pointing 60 degrees to the
right represents the B phase north to south contribution to the picture (coils B1
to C1) and the half length vector pointing 60 degrees to the left represents the
C phase north to south contribution (figure 33A). At time
 the full length
vector (phase A contribution) points, north to south, from the coil A2 position
with the phase B contribution (coil B2 to C2) at 60 degrees to the left, and the
phase C contribution (coil C1 to B1) at 60 degrees to the right (figure 33B).
the full length
vector (phase A contribution) points, north to south, from the coil A2 position
with the phase B contribution (coil B2 to C2) at 60 degrees to the left, and the
phase C contribution (coil C1 to B1) at 60 degrees to the right (figure 33B).
![[phase A flux]](./big/pmg/fnfig-33.jpg)
But, "wait!," you say. Aren't the phase separations 120 degrees? Where did
those angles of 60 degrees come from? Well, that's really just a bit of
geometric handwaving coupled with the knowledge of how our armature phase
coil groups are wired. In discussing figure 28, we noted how the B and C
phase field contributions are polarized due to their phase group coil wiring.
A little squinting at figure 28 will reveal that relative to the center of
the armature ring, directly at the edge of the armature ring, the contributions
of the B and C phases point at 60 degrees relative to the phase A component.
The fact that the sum of the angles of the B and C field contributions sum
to 120 degrees is really just a coincidence, and is related to the number of
coils on the armature ring. A different number of coils in the phase groups
would give a similar picture, but the angles would be different. The important
thing to remember here is the phase input vectors and the magnetic field
vectors are, of course, strongly related, but not the same. The phase input
provides current flow, and current flow through the wire creates the field.
Note that the picture at time
 is simply a
version of the picture at time
is simply a
version of the picture at time
 rotated by
180 degrees about the center of the armature ring. Not coincidentally, 180
degrees is the amount of phase rotation we see from time
rotated by
180 degrees about the center of the armature ring. Not coincidentally, 180
degrees is the amount of phase rotation we see from time
 to time
to time
 . That is, when our
input phases have rotated 180 degrees, it appears that so do our magnetic field
flux vectors. We can produce the same kind of figures for times
. That is, when our
input phases have rotated 180 degrees, it appears that so do our magnetic field
flux vectors. We can produce the same kind of figures for times
 and
and
 (phase C maximums),
and times
(phase C maximums),
and times
 and
and  (phase B
maximums), where the diagrams for times
(phase B
maximums), where the diagrams for times
 and
and
 will be versions of
the
will be versions of
the  and
and
 diagrams rotated
120 degrees clockwise, and the diagrams for times
diagrams rotated
120 degrees clockwise, and the diagrams for times
 and
and
 will be versions of
the
will be versions of
the  and
and
 diagrams rotated
clockwise 240 degrees (figure 34).
diagrams rotated
clockwise 240 degrees (figure 34).
![[rotating field]](./big/pmg/fnfig-34.jpg)
One more thing to note is we are referencing our rotation to the center of
the armature ring, and what we really have is a south magnetic field on
one side of the ring, and a north magnetic field on the opposite side of the
ring, The magnetic field rotation is of both the poles. We have been drawing
our diagrams to reference the south magnetic part of the field, but the north
magnetic field part rotates along with it, in sync, around the opposite side
of the armature ring.
At this point we basically have our rotating magnetic field. At least we can
see at times  ,
,
 ,
,
 ,
,
 ,
,
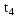 ,
and
,
and 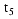 we have the same
magnetic field flux pattern rotated at 60 degree increments around the armature
ring, where 60 degrees is the amount of phase rotation seen between each time
step.
we have the same
magnetic field flux pattern rotated at 60 degree increments around the armature
ring, where 60 degrees is the amount of phase rotation seen between each time
step.
Another important thing to note in figure 34 is that it is not the flux vector
for phase A that is rotating around the armature ring. You can see in the
figures for each time step that the main flux comes from which ever phase
is at its positive or negative maximum value. If you compare the phase group
coil layout around the armature ring of figure 28 with the time step diagrams
in figure 34, you can see that the spacing of the coils results in the equal
spacing of the direction of the flux vectors around the armature ring. Since
we can't really tell one flux vector from another, what we see is an apparent
rotation of a single flux vector with time.
For the complete picture we would need to look at what happens between the
points of phase magnitude maximums. But, for this discussion, that is really
more than we need to do here. The bottom line is as the phase inputs vary for
times away from the phase input maximums, the fluxes from the phase
group coils will sum up as vectors to create a total flux picture which looks
basically like what we see for the phase magnitude maximums, but with the
head and tails for the main sum vector directed somewhere between the phase
group coils, rather than directly through an opposing set of coils. (Remember,
the diagrams we have seen are simple representations of a more complex
picture.) In the end we have a magnetic field flux vectors generated by the phase
coil groups which vary so we end up with a set of north and south pole fields
moving around the armature ring such that they appear to smoothly rotate.
Whew! Finally! A rotating magnetic field. Wow, that was kind of like pulling
teeth, wasn't it? Well, as Blaise Pascal once said, "I made this letter long
because I didn't have time to make it shorter." I may clean this up a bit
someday. But, don't hold your breath. For now, lets continue on the trail
of that oft promised, but yet to be seen self-starting single-phase motor.
Finding Another Way:
The final key to understanding the self-starting single-phase motor is seeing
why a polyphase motor spins in a given direction, and how it can be made to
spin in the opposite direction. The direction of rotation is determined by
the sequence order of the input phases. It will also be helpful to understand
a bit more of the possible wiring configurations for a motor/generator. So,
first will take a look at series and parallel wiring arrangements, then we'll
get on with the matter of direction of rotation.
Series and parallel and such:
We've hinted at other possibilities for armature coil phase group wiring
configurations before, noting that wiring coils end-to-end, with proper
consideration of phase angles, allows addition of the voltages generated
in each coil. This means that besides putting more turns in our coils to
generate higher voltages, which can make motor/generator construction
problematic due to large coil sizes, we can also use smaller coils wired
end-to-end (formally called a series connection) to achieve higher voltage
outputs. For a single-phase motor/generator such as the one illustrated in
figure 3 this is simply a matter of adding more coils to the armature ring,
and an equal number of magnets added to the rotor disc. In the case of
polyphase motor/generators like the ones depicted in figures 6 and 22, to
increase output voltage we would add equal numbers of coils to each phase
coil group, and add magnets on the rotor disc following the constraints
given by the design equations provided in the rote formula discussion.
Phase sequences:
Forward/reverse:
Split phase start:
yatayatayata...
Slogging Through Cogging:
eddy currents and such...
Rote Revisited:
To be continued...?
References:
(Clicking reference numbers here returns you to the text you came from.)
[1] http://www.otherpower.com/woodmill.html
[2] http://www.alton-moore.net/wind_turbines.html
[3] Electric Motor Repair. Robert Rosenberg,1946. Murray Hill Books, Inc.
[4] Design of Brushless Permanent-Magnet Motors. J.R.Hendershot Jr. and Tje
Miller,1994. Magan Physics Publishing and Clarendon Press.
[5] Permanent Magnet Motor Technology: Design and Applications, Second Ed.,
Revised and Expanded. Jack F. Gieras and Mitchell Wing,2002. Marcel Dekker, Inc.
[6]Handbook of Electric Motors, Second Edition, Revised and Expanded. Hamid A. Toliyat and Gerald B. Kilman (eds.),2004. Marcel Dekker, Inc.
Last updated 03August2008
Alan Swithenbank, alans@cuervo.stanford.edu
![[hand crank]](./thumb/pmg/pmgcrank_18-t.jpg)
![[Rainforest Site]](./gifs/rainforest.gif)
![[new]](./gifs/new.gif) Click here for my mark-II boundary layer turbine page.
Click here for my mark-II boundary layer turbine page.
![[new]](./gifs/new.gif) Click here for my miscellaneaganza! page.
Click here for my miscellaneaganza! page.
![[best use any browser]](./gifs/vbrowser.gif)
![[under construction]](./gifs/constr.gif)
![[coil winder]](./thumb/pmg/coil_winder_1-t.jpg)
![[coil winder]](./thumb/pmg/coil_winder_2-t.jpg)
![[coil winder]](./thumb/pmg/coil_winder_3-t.jpg)
![[coil winder]](./thumb/pmg/coil_winder_4-t.jpg)
![[magnetite]](./thumb/pmg/magnetite_3-t.jpg)
![[magnetite]](./thumb/pmg/magnetite_2-t.jpg)
![[magnetite]](./thumb/pmg/magnetite_1-t.jpg)
![[cast iron]](./thumb/pmg/cast_iron_2-t.jpg)
![[cast iron]](./thumb/pmg/cast_iron_1-t.jpg)
![[armature]](./thumb/pmg/armature_1-t.jpg)
![[armature]](./thumb/pmg/armature_2-t.jpg)
![[armature]](./thumb/pmg/armature_3-t.jpg)
![[rotor]](./thumb/pmg/rotor_1-t.jpg)
![[rotor]](./thumb/pmg/rotor_3-t.jpg)
![[rotor]](./thumb/pmg/balance_1-t.jpg)
![[frame]](./thumb/pmg/axle_1-t.jpg)
![[frame]](./thumb/pmg/frame_1-t.jpg)
![[frame]](./thumb/pmg/frame_2-t.jpg)
![[bearings]](./thumb/pmg/bearing_1-t.jpg)
![[bearings]](./thumb/pmg/bearing_2-t.jpg)
![[coils]](./thumb/pmg/winding_1-t.jpg)
![[coils]](./thumb/pmg/winding_2-t.jpg)
![[coils]](./thumb/pmg/winding_3-t.jpg)
![[coils]](./thumb/pmg/winding_4-t.jpg)
![[coils]](./thumb/pmg/winding_5-t.jpg)
![[coils]](./thumb/pmg/winding_6-t.jpg)
![[coils]](./thumb/pmg/winding_7-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_1-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_2-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_3-t.jpg)
![[mounting]](./thumb/pmg/coil_mount_4-t.jpg)
![[connections]](./thumb/pmg/connection_5-t.jpg)
![[connections]](./thumb/pmg/connection_3-t.jpg)
![[connections]](./thumb/pmg/connection_1-t.jpg)
![[connections]](./thumb/pmg/connection_2-t.jpg)
![[mot/gen]](./thumb/pmg/mot_gen_1-t.jpg)
![[mot/gen]](./thumb/pmg/mot_gen_2-t.jpg)
![[mot/gen]](./thumb/pmg/mot_gen_4-t.jpg)
![[phase wiring]](./thumb/pmg/mot_gen_phs_1-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_1-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_2-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_3-t.jpg)
![[phase wiring]](./thumb/pmg/phase_wiring_4-t.jpg)
![[testing]](./thumb/pmg/testing_2-t.jpg)
![[testing]](./thumb/pmg/testing_1-t.jpg)
![[testing]](./thumb/pmg/testing_3-t.jpg)
![[testing]](./thumb/pmg/testing_4-t.jpg)
![[phase A-B]](./thumb/pmg/phase_a-b-t.jpg)
![[phase B-C]](./thumb/pmg/phase_b-c-t.jpg)
![[phase A-C]](./thumb/pmg/phase_a-c-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_01-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_02-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_03-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_04-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_05-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_06-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_07-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_08-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_09-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_10-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_11-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_12-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_13-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_14-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_15-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_16-t.jpg)
![[hand crank]](./thumb/pmg/pmgcrank_17-t.jpg)
![[hand crank]](./thumb/pmg/pmghandle_01-t.jpg)
![[hand crank]](./thumb/pmg/pmghandle_02-t.jpg)
![[hand crank]](./thumb/pmg/pmghandle_03-t.jpg)
![[new magnets]](./thumb/pmg/neodymium_01-t.jpg)
![[new magnets]](./thumb/pmg/neodymium_02-t.jpg)
![[new magnet test]](./thumb/pmg/neotest_01-t.jpg)
![[new magnet test]](./thumb/pmg/neotest_02-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_01-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_02-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_03-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_04-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_05-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_06-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_07-t.jpg)
![[3 phase rect]](./thumb/pmg/3phsrect_08-t.jpg)
![[3 phase rect test]](./thumb/pmg/recttest_01-t.jpg)
![[3 phase rect test]](./thumb/pmg/recttest_02-t.jpg)
![[coil diagramming]](./big/pmg/fnfig-01.jpg)
![[single phase coils]](./big/pmg/fnfig-02.jpg)
![[single phase build]](./big/pmg/fnfig-03.jpg)
![[polyphase groups]](./big/pmg/fnfig-04.jpg)
![[polyphase connections]](./big/pmg/fnfig-05.jpg)
![[polyphase build]](./big/pmg/fnfig-06.jpg)
![[magnet flux lines]](./big/pmg/fnfig-07.jpg)
![[left hand rule]](./big/pmg/fnfig-08.jpg)
![[wire loop flux lines]](./big/pmg/fnfig-09.jpg)
![[wire coil flux lines]](./big/pmg/fnfig-10.jpg)
![[simple electric motor]](./big/pmg/fnfig-11.jpg)
![[magnet creates current]](./big/pmg/fnfig-12.jpg)
![[multiple wires multiple currents]](./big/pmg/fnfig-13.jpg)
![[coiled wire bigger current]](./big/pmg/fnfig-14.jpg)
![[circle to line machine]](./big/pmg/fnfig-15.jpg)
![[creating a sinusoid]](./big/pmg/fnfig-16.jpg)
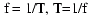 .
.
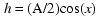
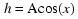
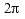 radians in 360
degrees (making one radian approximately 57.297 degrees). So, one rotation of
the disc in figure 15 means the peg which moves the crossbar sweeps through an
angle of
radians in 360
degrees (making one radian approximately 57.297 degrees). So, one rotation of
the disc in figure 15 means the peg which moves the crossbar sweeps through an
angle of  )
is a measure of the speed of rotation of a disc in terms of radians per second,
rather than cycles per second. Again, we aren't really talking about speed of
rotation of a disc, but the "speed" with which a sinusoidal waveform
completes its repeated identical excursions. The concept of radial velocity
still applies, since that sinusoid has the same circular motion related form
as the one produced by the disc and pen method of figure 15. In either case,
multiplying the radial velocity by time (measured in seconds) gives us radians
as a proper argument to the cosine function, and, thus, knowing the radial
velocity, we can plot our sinusoid against time on the x-axis of an x-y plot,
rather than degrees. That brings us to a new form for our equation:
)
is a measure of the speed of rotation of a disc in terms of radians per second,
rather than cycles per second. Again, we aren't really talking about speed of
rotation of a disc, but the "speed" with which a sinusoidal waveform
completes its repeated identical excursions. The concept of radial velocity
still applies, since that sinusoid has the same circular motion related form
as the one produced by the disc and pen method of figure 15. In either case,
multiplying the radial velocity by time (measured in seconds) gives us radians
as a proper argument to the cosine function, and, thus, knowing the radial
velocity, we can plot our sinusoid against time on the x-axis of an x-y plot,
rather than degrees. That brings us to a new form for our equation:
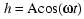

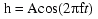 ,
,
![[lead vs. lag]](./big/pmg/fnfig-17.jpg)
![[cosine lead vs. lag]](./big/pmg/fnfig-18.jpg)
 ,
,
 , may be positive
or negative, and, as used here, should be expressed in radians. If
, may be positive
or negative, and, as used here, should be expressed in radians. If
 and divide by 180 to
convert degrees to radians, which leaves us with the same basic form of the
equation:
and divide by 180 to
convert degrees to radians, which leaves us with the same basic form of the
equation:
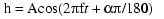 ,
,

 . We can make one
more simplification that has its origin in standard practice rather than
physics, which is when comparing phases, we assume the phase angle for the
first phase is zero, and adjust the other phase angles accordingly. That gives
us, in our three phase case, the following simplified equation set:
. We can make one
more simplification that has its origin in standard practice rather than
physics, which is when comparing phases, we assume the phase angle for the
first phase is zero, and adjust the other phase angles accordingly. That gives
us, in our three phase case, the following simplified equation set:

![[3-phase lead/lag]](./big/pmg/fnfig-19.jpg)

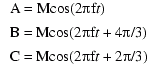
![[PolePhase.c]](./thumb/pmg/polephase_c-t.jpg)
![[3-phase waveforms]](./thumb/pmg/phasediag-t.jpg)
![[numeric output]](./thumb/pmg/polephase_data-t.jpg)
![[elec. vs. mech. degrees]](./big/pmg/fnfig-20.jpg)
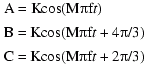

 +
+
 +
+
 =
=
 =
=
![[Y configuration]](./big/pmg/fnfig-21.jpg)
![[Y motor/generator]](./big/pmg/fnfig-22.jpg)
![[Y 3 and 4 wire connections]](./big/pmg/fnfig-23.jpg)
![[coil and line voltages]](./big/pmg/fnfig-24.jpg)
 * Coil Current =
Line Current
* Coil Current =
Line Current
 , where r
is the distance from the center of the dipole. (This is different than the fall
off from a monopole, such as a positive or negative electric charge, where
field strength falls off as
1/
, where r
is the distance from the center of the dipole. (This is different than the fall
off from a monopole, such as a positive or negative electric charge, where
field strength falls off as
1/ .)
.)
![[1/(r**3)]](./big/pmg/fnfig-25.jpg)
![[magnetic 'bumps']](./big/pmg/fnfig-26.jpg)
![[6 pole armature]](./big/pmg/fnfig-27.jpg)
 , to be the zero
degree position for phase A, take time two,
, to be the zero
degree position for phase A, take time two,
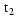 , to be the zero
for phase B, (120 degrees for phase A), and take time four,
, to be the zero
for phase B, (120 degrees for phase A), and take time four,
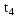 , to be the zero
degree position for phase B, (240 degrees for phase A). Note, relative to the
waveforms in figure 19, this means at time
, to be the zero
degree position for phase B, (240 degrees for phase A). Note, relative to the
waveforms in figure 19, this means at time
![[6 pole armature]](./big/pmg/fnfig-28.jpg)
![[angle change rotation]](./big/pmg/fnfig-29.jpg)
![[phasor vs. machine]s](./big/pmg/fnfig-30.jpg)
![[rotating vector]](./gifs/pmg/Phasor-t.jpg)
![[figure-eight]](./big/pmg/fnfig-31.jpg)
![[figure-eight phasor]](./gifs/pmg/Mag-t.jpg)
![[3-phase figure-eights]](./big/pmg/fnfig-32.jpg)
![[triple phasor]](./gifs/pmg/3Mag-t.jpg)
 . Except this time
instead of producing another picture like figure 28 we'll use vectors to make our
graphic representation.
. Except this time
instead of producing another picture like figure 28 we'll use vectors to make our
graphic representation.
![[phase A flux]](./big/pmg/fnfig-33.jpg)
 and
and
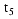 (phase B
maximums), where the diagrams for times
(phase B
maximums), where the diagrams for times
![[rotating field]](./big/pmg/fnfig-34.jpg)