An important subfield of physics -- nuclear physics -- deals with the smallest particles of which matter is composed. Constructs developed by Kenneth Arrow [Arrow 1964] and Gerard Debreu [Debreu 1959] provided a similar foundation for financial economics. The resulting approach is often called the Arrow-Debreu Paradigm. It characterizes promised future payments in terms of both the times at which payments are to be made and the states of the world that must obtain for payments to be made. Hence the often-used name: the time-state paradigm.
Since the approach represents securities and other types of financial instruments in terms of their most elemental components, one could as well title it: Nuclear Financial Economics.
We start with the simplest possible example that involves both time and uncertainty. There are two time periods:
0: today
1: a year from now
There are also two possible future states of the world:
G: the weather over the next year will be good
B: the weather over the next year will be bad
The states of the world are mutually exclusive (if one occurs, the other cannot) and exhaustive (one of them must occur).
The economy is very simple indeed. The only commodity is the apple and there is no money per se. In effect, the apple is the unit of currency.
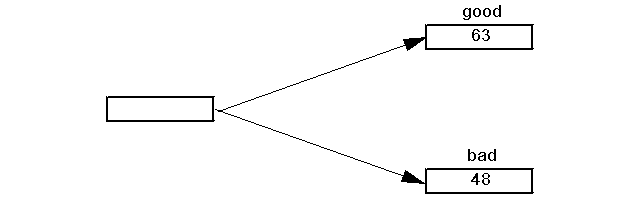
The only type of productive investment in this economy is, not surprisingly, an apple tree. We focus initially on a tree that will produce:
63 apples if the weather is good
48 apples if the weather is bad
This is shown in the figure below. Time proceeds from left to right. The box on the left refers to present value. The boxes on the right represent alternative states of the world. One but only one of the states of the world in a vertical position will take place at the time in question. The names of the states are indicated at the tops of the boxes. The numbers inside the boxes indicate the payoffs.

In our economy there are three elemental time-state claims:
One apple at time 0 (today)
One apple at time 1 if the weather is good
One apple at time 1 if the weather is bad
In keeping with our interpretation of the Arrow-Debreu approach as Nuclear Financial Economics, we will call these atomic time-state claims. Note that the latter two descriptions include the item (apple), the number of units (one), the time at which delivery is to be made (0 or 1), and the state of the world that must obtain for delivery to be made (good or bad weather). In the case of the first description, no state is given, since present values are not conditional on future states of the world. To simplify the exposition, we will refer to these claims as:
One "present apple" (PA)
One "good weather apple" (GA)
One "bad weather apple" (BA)
with the understanding that these are simply shorthand descriptions.
In principle, any investment vehicle can be considered to be composed of such atomic claims. Thus the output of our apple tree is equivalent to a 63 GAs and 48 BAs.
Many of the fundamental concepts of Financial Economics are based on the assumption that markets exist in which claims can be traded efficiently (at low cost). We begin with the assumption that dealers stand ready to trade atomic claims and to do so without cost. As will be seen, these dealers are a bit of an artifice. Later we consider more realistic assumptions about the world.
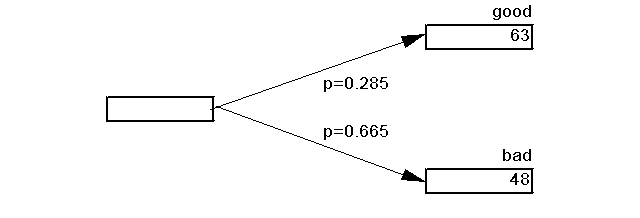
Assume that Dealer G "makes a market" in good weather apples. In particular, she is willing to trade (swap):
0.285 present apples for 1.000 good weather apples
or
1.000 good weather apples for 0.285 present apples
or any multiple thereof (dividing apples into pieces, as required).
This can better be understood in standard financial terms. Assume that an owner of an apple tree has issued a certificate of the following form:
I, __________ promise to deliver to the bearer of this certificate
one apple at the end of year ____ if (but only if) the weather
during the year has been good.
In standard parlance, this piece of paper (or its electronic equivalent) would be termed a security. Assume that a credit-rating agency has examined the property of the apple grower (the apple tree) and has established that no more than 63 of these securities have been issued and that there are no other claims on the grower's assets in the event of good weather. As a result, the securities are rated AAA ("triple-A") and can be considered default-free.
Under these conditions, the security in question represents a property right in an atomic time-state claim. In a sense, it is thus an atomic security or, given the origin of the concept, an Arrow-Debreu security.
The price of this security is 0.285 present apples, since the dealer stands ready to trade this number of present apples for the security. More generally, the price of any security is the amount of the relevant numeraire paid immediately for which the security can be traded. Note that the ability to make a trade is central to the definition of a price.
In the real world, of course, dealers charge more to sell a security than they are willing to pay to buy it. The spread between the ask (selling) and bid (buying) price provides compensation for the market-making function. In our examples we assume (unrealistically) that there is no such spread and hence that there is but one price. In practice, the average of the bid and ask prices is often used as a surrogate for "the price". For detailed computations, of course, the specifics of a proposed transaction may need to be taken into account and the relevant price (bid or ask) used.
This diversion completed, we return to our world of non-profit dealers.
In addition to Dealer G, we assume that another, Dealer B, is willing to trade (swap):
0.665 present apples for 1.000 bad weather apples
or
1.000 bad weather apples for 0.665 present apples
or any multiple thereof (again, dividing apples into pieces, as required).
The trading environment is shown in the figure below.
Thus far we have a world with three types of time-state claims (PA, GA and BA). Explicit markets exist for trading (1) PA and GA and (2) PA and BA. Note that each such trade has the characteristic of an investment -- today's goods are traded for the prospect of goods in the future. Thus one purchasing a GA atomic security can be said to have invested 0.285 (present) apples to obtain 1.000 apples in the future if the weather is good.
But what of the other possible type of trade in this world? What would it mean to trade good weather apples for bad weather apples? How might one accomplish this? And what would be the terms of trade?
To answer these questions, consider the following agreement:
Party A promises to pay party B: 6 apples if the weather is good
Party B promises to pay party A: 3 apples if the weather is bad
Neither party pays the other anything today (on signing)
Such an agreement is called a swap in financial parlance. It represents the third possible type of trade in our simple world: GA for BA.
Is this a fair deal? If one desires an answer based on ethical considerations, other disciplines will have to be invoked. Financial Economics can only indicate whether or not one of the parties could get a better deal elsewhere.
Assume that Party A comes to you with the proposal that you sign the agreement as Party B. You are willing to give up 3 apples if the weather is bad in order to increase your consumption if the weather is good. But is 6 apples the best that you can do?
To answer the question, consider the following alternative trades:
Go to dealer B, trade 3 BA for 3*0.665 = 1.995 PA
Go to dealer G, trade 1.995 PA for 1.995/0.285 = 7 GA
The net result is, of course, to trade 3 BA for 7 GA -- a better deal than offered by canny Party A, who will have to search elsewhere for a counterparty foolish enough to take the deal.
Note that although explicit markets are being made in only future atomic time-state claims, it is possible to "create" trades involving any present and future claims. This is a perfectly general result. If one can trade each possible future atomic time-state claim for present units of a numeraire, any desired trade can be accomplished. Thus a set of atomic security prices is sufficient for accomplishing any desired trade.
Consider two people sharing a pizza. To insure an even division, it is wise to agree that one party should cut it, and the other should choose his or her piece. Similarly, it is useful to require someone offering a bet on a sporting event to be willing to take either side on the offered terms. With this in mind, we return to Party A and Party B.
Assume that a securities firm is willing to serve as either Party A or Party B in the previously-described swap (6 GAs for 3 BAs). Clearly, you have no interest in being Party B. But what about serving as Party A? Consider the following set of trades:
Sign the Agreement as party A (pay 6 GA, get 3 BA)
Go to dealer B, trade 3 BA for 3*0.665 = 1.995 PA
Go to dealer G, trade 6*0.285 = 1.710 PA for 6 GA
It is useful to put all this information in a payment matrix with each row representing a time-state combination and each column a transaction. Conventionally, we represent outflows with negative numbers, inflows with positive numbers, and neither with zeros.
Agreement Dealer B Dealer G
Present 0 + 1.995 - 1.710
Good weather - 6.0 0 + 6.0
Bad weather + 3.0 - 3.0 0
Of particular interest is the sum of the payments in each row, shown in the final column below:
Agreement Dealer B Dealer G Net
Present 0 + 1.995 - 1.710 + 0.285
Good weather - 6.0 0 + 6.0 0
Bad weather + 3.0 - 3.0 0 0
Note what this set of transactions accomplishes -- getting something for nothing! Moreover, there is no reason to settle for such a small gain. Double the sizes of all the transactions and the net gain is doubled. Quadruple them and the gain is quadrupled.
Well and good, but what if one really wanted apples next year if the weather is good. Not to worry. Add a final trade in which 0.285 present apples are traded for 1.000 good weather apples. Want bad weather apples? Add a trade to convert the gains into the appropriate payment. No matter what a person's preferences may be, it is desirable to exploit the foolishness of the firm offering this swap.
Too good to be true? Probably. This example constitutes an arbitrage -- every trader's dream. To formalize:
An arbitrage provides a positive net payoff in at least one time
and state and no negative net payoff in any time and state.
An arbitrage is thus a money machine (or, as in this case, an apple machine). When an opportunity of this type arises, traders will rush to exploit it, causing others to adjust their terms of trade until swap terms involve no arbitrage.
A set of swap terms that does not permit arbitrage is arbitrage-free.
In an important sense, every security transaction can be considered a swap. The purchase of an atomic security is a swap of present goods for conditional future goods. The sale of such a security is a swap of conditional future goods for present goods. Such cases, when one "side" of the swap involves present goods or services, are typically termed investments. Thus one invests present apples in the hope of obtaining more apples in the future. But note that the swap of good weather apples for bad weather apples is no different in kind, even though no goods or services are exchanged at the time of the agreement.
To be explicit, we refer to swaps of this latter kind as zero-investment strategies. As with other transactions, they are represented by cash flow vectors with positive and negative numbers, but with zeros in the first (present) row.
