Algorithm

Optimization:

Given a graph 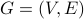G=(V,E) , with vertex set V=[n] , and an integer , we attempt to solve the following non-convex problem:

$begin{array}{ll} {rm maximize} & sum_{(i,j)in E} sigma_icdotsigma_j-frac{gamma}{2}big|Mbig|_2^2 {rm subj. to} & |sigma_{i}|_2 = 1; forall iin [n], end{array}$

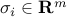where $Mequivsum_{i=1}^nsigma_i$ , and $sigma_i in {mathbf R}^m$ .

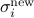We use block-coordiate ascent, where at each step we maximize over the vector sigma_i . Namely at each step, we draw iin [n] uniformly at random and update sigma_i to $sigma^{{rm new}}_i$ given by

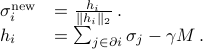
$begin{array}{ll} sigma^{{rm new}}_i & = frac{h_i}{|h_i|_2}, . h_i & = sum_{jin partial i}sigma_j - gamma M, . end{array}$

where partial i denotes the set of neighbors of in .

Projection:

Once an (approximate, local) maximizer is obtained, we construct an embedding of vertices as follows.

Compute the empirical covariance

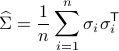
$widehat{Sigma} = frac{1}{n}sum_{i=1}^nsigma_isigma_i^{sf T}$

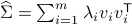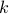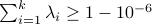Compute its eigenvalues end eigenvectors $widehat{Sigma}=sum_{i=1}^mlambda_i v_iv_i^{sf T}$ , with . Note that, by construction $sum_{i=1}^mlambda_i=1$ . Let be the smallest index such that $sum_{i=1}^klambda_ige 1-10^{-6}$ .

Return, for each vertex , the projections on the 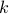leading eigenvectors 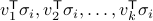$v_1^{sf T}sigma_i, v_2^{sf T}sigma_i, dots,v_k^{sf T}sigma_i$ . Notice that these coordinates are ordered by ‘importance.’

We observe empirically that 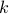is often smaller than . The dimension of the embedding can be further reduced by only using the first k'<k dimensions (for some 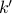chosen by the user).

How to choose the input parameters:

The user must specify three parameters:

The number of components . The algorithm is pretty insensitive to this choice, and we found that 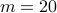works in most cases (in the sense that the optimization converges to a global maximum). Indeed, this choice appears to be conservative and often 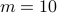or smaller works as well. For very large instances (above 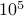vertices), it might be useful to use larger values, e.g. .

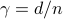The regularization parameter . The default choice , with 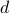the average degree, seems appropriate in most cases.

The number of iterations. Each iteration corresponds to 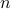block updates. We obtained satisfactory results with 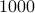iterations or less.