Non-negative Matrix Factorization via Archetypal Analysis
Overview
 |
Motivation: Given a collection of Method: Our approach builds upon an idea that can be traced back to the work of Cutler and Breiman in their paper on ‘Archetypal Analysis’. Our proposed method does not require the data to be separable, while it provides a generally unique decomposition. The cost function that we minimize, is the sum of two objectives: the first one is the sum of the distances of the data points from the convex envelope of the archetypes. This can be interpreted as the empirical risk in writing the data points as a convex combination of archetypes. The second objective is the sum of the distances of archetypes from the convex envelope of the data points (which can be viewed as a data-dependent regularization, encouraging archetypes to be similar to the data points). Hence, in some sense, we are optimizing a trade-off between bias and variance terms which enables us to get a robust estimation under fairly general conditions. Optimization: While our method requires solving a nonconvex optimization problem, we find standard optimization methods succeed in finding good solutions for real and synthetic data. In our code, we have implemented Proximal Alternating Linearized Minimization (PALM) algorithm (both normal and accelerated versions). This algorithm is guaranteed to converge to critical points of the risk function. Further, we use a reasonable initial point by approximating the data as separable. Using such initialization helps the first order, descent PALM algorithm to get close to the global minimum of our nonconvex objective. This website provides an overview of our method along with its impelementation in Python. We would greatly appreciate your feedback, especially in cases where the algorithm appears to fail. In such a case please send us the data that you use or let us know how to repeat your experiments. Please send any feedback to hrhakim at stanford.edu or montanari at stanford.edu. |
Example
The following plot from the results of an spectral unmixing experiment with a synthetic data demonstrates the performance of our mehtod. The original spectra are shown in red and the recovered spectra using our approach and two other common methods for NMF can be seen in blue. We have provided the Python program for repeating these experiments in the Code section. For full description of this experiment please refer to our paper.
 |
Paper
H. Javadi and A. Montanari, Non-negative Matrix Factorization via Archetypal Analysis, 2017
People
Related Papers
Jerome Bolte, Shoham Sabach, and Marc Teboulle, Proximal alternating linearized minimization for nonconvex and nonsmooth problems, Mathematical Programming 146 (2014), no. 1-2, 459-494.
Adele Cutler and Leo Breiman, Archetypal analysis, Technometrics 36 (1994), no. 4, 338-347.
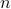 data points
data points 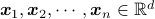 ,
we would like to express them
as convex combination of a small
set of
,
we would like to express them
as convex combination of a small
set of  ‘archetypes’,
‘archetypes’, 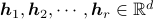 .
This representation is not always unique
and prior works have studied it and its robust estimation under
the separability condition and its generalizations.
This condition requires that the true archetypes or
the weights are non-negative and sufficiently sparse.
.
This representation is not always unique
and prior works have studied it and its robust estimation under
the separability condition and its generalizations.
This condition requires that the true archetypes or
the weights are non-negative and sufficiently sparse.