If there is a problem you can't solve, then there is an easy problem you can solve: find it. George Pólya, 1945
Ionic polymers & electrolytes
☞ Electrostatics-driven polymer assembly
Two families of ionic polymers are investigated in our group: salt-doped block copolymers (SdBC) and polyelectrolyte solutions (PEs). SdBC are of interest because of their potential as separation membrane for lithium-ion batteries. By designing materials that include both glassy and ion-dissolving components, the membrane exhibits the necessary mechanical and functional properties. PEs are a model system for studying the fundamentals of the aggregation behavior of ionic polymers in aqueous solutions, which underlies numerous industrial processes such as E-ink encapsulation, food flavoring, underwater adhesives, and provides a platform for investigating biomolecule aggregation, most of the latter being ionic polymers as a first approximation. The commonality of these ionic systems is the competition of multiple length scales, the primary ones being the Debye screening length and radius of gyration of polymers or the characteristic domain sizes. We combine continuum mechanics descriptions and atomistic scale modeling to investigate the macroscopic phase behavior and how it couples to ionic transport. [Publications: 22, 23, 27, 31, 42, 45, 47, 48, 50, 52, 53, 56, 63]
We work closely with experimental colleagues. With Balsara group at Berkeley, we showed that the self-assembled morphology of SdBC systems can be surprisingly well captured by the selective ion solvation, which results from the propensity of ions being solved in high permittivity dielectrics (PEO mostly). Such selective solvation completes with translational entropy of dissolved ions. We further showed, theoretically, two distinct thermodynamic regimes can be identified based on the strength of ion solvation, one dominated by solvation whereas the other dominated by entropy. In the work of PEs, we extensively collaborate with Xia group in the Chemistry department of Stanford. We designed, and synthesized a family of homologous polycations and polyanions that have identical backbone and that are fluorescently labeled. The simplicity of this chemical design enable us to generate several sets of phase diagrams showing how a range of molecular scale factors influences the complexation thermodynamics (coacervation), including the effects of backbone polarity, mixing stoichiometry, and ion valency. These results are rationalized by our molecule-informed theoretical models that considers charge connectivity, ionic screening, and ion-binding equilibrium. One of the unexpected discoveries the emergence of loop-in complexation in highly non-stoichiometric mixtures, which we rationalize using the picture of Donnan equilibrium. [Publications: 72, 73][Codes on iPSCF (ionic self-consistent field theory)]
☞ Polymer interphases for lithium dendrite suppression
Lithium metal anodes are required for high energy density next-generation batteries, with applications in electric vehicles, grid-scale storage, and personal devices. However, during charging, spontaneous growth instabilities known as “dendrites” can lead to short circuiting and electrolyte degradation, causing significant safety and performance concerns. Recently, soft polymeric interphases between the lithium metal anode and the electrolyte have been shown to suppress dendritic growth, overturning the predictions of existing theoretical approaches. We use coarse-grained molecular simulations and develop analytical theory to understand how polymer permittivity, viscoelasticity, and thickness alter the stability and morphology of electrodeposition. [Publications: 62, 92]
The coarse-grained simulations provides a convenient means for screening parameters that may influence the morphology of ion deposition. The fundamental questions about why those parameters work the way the do have to be addressed with more elementary analyses. As a start, we analyzed the stability of the ion-deposition process. Our continuum model contains three components: the transport of ions, the reduction of the ions at the interface, and the mechanical responses. The standard linear perturbation treatments revealed that the growth instability is sensitive to both the modulus ratio between polymer and metallic anode, and to the value of partial molar volume of lithium ions, due to the dependence of ionic chemical potential on the volumetric work while being reduced.
☞ Ion solvation & transport in designed electrolytes
Together with our experimental colleagues, Cui and Bao groups at Stanford, we have demonstrated recently that molecular engineering of liquid is an effective approach for enhancing cycling stability and coulombic efficiency current Li metal batteries and those required for commercial applications. A wide range of electrolytes and their mixtures have been investigated, which reveals that the solvation free energy of the lithium ions in the electrolyte plays an important. It needs to be substantial, in order to generate enough freely moving ions; yet it can not be too strong, so that the SEI may not be dominated by solvent derivatives. By iterative experimental-theoretical studies, we are continuing to explore different strategies to engineering the solvation potential and to optimize the ion conductivity, which includes the tuning of the fraction of polar groups, the steric effects, blending, etc. Our theoretical efforts in this space rely heavily on using atomistic simulations to reveal and quantify the solvation structure, evaluating the solvation free energy, and calculating (expensive!) the coupled ion transport coefficients! [Publications: 75, 82, 88, 91, 94]
Polymers with intricate topology or architecture
☞ Conjugated polymers & ribbon-like chains
PEDOT:PSS is a conducting polyelectrolyte complex investigated for a variety of applications, including thermoelectrics, optoelectronics, and flexible sensors. While experimental studies offer empirical insight into its device performance and microscopic morphology, inaccessibility of smaller length scales leaves incomplete an understanding of how nanoscale behavior of PEDOT:PSS gives rise to its macroscopic transport properties. As computational approaches facilitate a direct investigation of molecular behavior, we endeavor to bridge this knowledge gap, discerning how synthesis and processing conditions affect morphology and material performance. We employ atomistic, coarse-graining and analytical techniques to retain detailed chemical information over multiple length and time scales. The ultimate goal is to develop a versatile framework for enhancing future engineering efforts of PEDOT:PSS and other conducting polymers. [Publications: 69, 71, 83]
A distinct feature of conjugated polymers and ladder polymers is the coplanar conjugation of the consecutive monomers that persist over long distances along the backbone, which can not be adequately accounted by the worm-like chain (WLC) model. Since the persistence length usually far exceeds the backbone contour length, the WLC model fails to capture the local correlations of planar normals. We are developing the ribbon-like chain model (RLC) that generalizes WLC, by including anisotropic bending stiffness and twisting stiffness. The model considers the correlations of both normal and tangent components, predicting three independent persistence lengths, which are governed by the strength of the deformation moduli. Finding out the moduli allows us to differentiate different types of conjugated polymers with greater and more accurate resolution.
☞ Reversible or dynamic polymer networks
Gel point is sharply defined, but gelation process is gradual. Before the first incidence of the infinitely percolating network is seen, a large number of smaller clusters have been formed, due to the finite crosslinking probability. The statistics for the number and the size these clusters evolves with the degree of crosslinking, and eventually determines when the gel point is reached and gelation or vulcanization is complete. Moreover, when the dynamic bonds are introduced in order to achieve desirable processability and healability, these clusters can dissociate or re-associate, giving rise to another distribution, for the lifetime, which changes fundamentally the dynamic and rheological behavior of the polymer networks. This statistical properties of these preformed clusters is usually broad, exhibiting a long power-law scaling. The window allowing for a convenient experimental study of these distributions is also narrow, shrinking as the length of precursor chains increases. We thus designed coarse-grained, hybrid MD/MC simulations to investigate the cluster statistics for dynamic polymer networks within the gelation window. We are keenly interested in the following questions: how does the distribution of cluster changes as the gel point is aproached; how are clusters packed spatially; how are defects such as dangling ends and loops distributed in the clusters; how does the above properties influence the location of the gel point and the conversion of precursor chains; and, eventually, how rapidly the cluster move and how the stress relaxes in these materials. [Publications: 84, 93, 57]
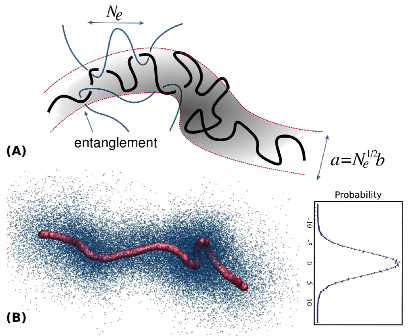
☞ Molecular basis of polymer entanglement
Stress relaxation in polymeric melts and concentrated polymer solutions is inconveniently slow. Since polymers adopt rather open random-walk configurations, when densely packed, they penetrate the neighboring chains significantly and mutually affect each other's motion. Chains can not cut through each other, and can only slide along the direction of their backbones. The stress of these mutual constraining effects is quantified by a material parameter, the entanglement molecular weight, which scales inversely with the elastic modulus of the material. We develop simulation and analysis tools to address questions including what constitutes an entanglement, how it depends on molecular parameters such as monomer bulkiness and chain stiffness, whether it is binary or collective, etc. We also perform long time molecular dynamics simulations to investigate the consequence of entanglement on the stress relaxation in polymer melts, aiming at elucidating the molecular mechanisms responsible for stress relaxation. Recently, we have devised an algorithm that allows us equilibrate the configurations of ring polymers in atomistic simulations; see movie below. [Publications: 13, 14, 17, 18, 21, 26, 30, 57, 58]
Charge polarization at dielectric interfaces
☞ Multiple-scattering theory for many-body polarization
A key feature of interfaces in multi-component systems is surface charge polarization. The charge distributions on opposite sides of the interface respond to an applied electric field differently, giving rise to the accumulation of net charge at the interface, the sign of which depends on the relative magnitudes of dielectric permittivities. These surface charges are relevant for water/air interfaces, surfaces of charged particulate mediums, cell membranes, liquid crystals, and many industrial processes such as fluidized beds and the processing of pharmaceutical particles. We develop analytic and numerical approaches to deal with phenomena correlated with surface charge polarization, and we are interested in aggregation thermodynamics and dynamics. [Publications: 29, 31, 34, 36, 37, 40, 43, 46, 51]
☞ Singular induced charges for contacting dielectrics
The induced surface charges depends on the ratio of the dielectric permittivity of the inclusion to that of the medium. The amount of induced surface charges between one pairs of approach particles increases as the gap distance decreases. Could such effect persists indefinitely? What is the limiting behavior when the gap distance is not only small, but vanishes? For metallic surfaces, which has an infinite static permittivity, a Derjaguin approximation shows that the amount of induced charges indeed diverge logarithmically with the distance for a finite difference in electrostatic potential. Generalizing such analysis to dielectric is much harder, in that the dielectrics are not equi-potential, requiring the distribution of the surface potential be resolved. However, such surface potential distribution strongly depends on the amount of surface charges induced, which we hoped to find out in the first place. By making an analogy with a heat transport problem in composites studied by Batchelor, we showed that the surface potential and surface charge can be self-consistently determined. There are in fact two types of singularities, one depending on the gap distance and another on the ratio of dielectric permittivities, both logarithmically. And, the metallic case is recovered as the permittivity ratio is nominally set to zero. Curvature of the contacting spheres matter as well, and the exact form is also known. Identifying this vexing singularity, and embedding the analytical forms into standard numerical packages finally allows us to calculate the exact polarization energy for aggregates of contacting dielectrics. Shown below is how the singular contact capacitance changes with permittivity and gap distance. [Publications: 85]