Assign3: Combinations

The mathematical combinations function C(n, k) counts the number of ways one can choose k things from a set of size n. A formula for counting combinations is based on the factorial function:

              n!
 C(n, k) =  -----------
            k! * (n-k)!

For example, an ice cream shop has 6 flavors on display. The shop is running a special on triple-scoop cones and offers that if you are the first person today to order a particular combo, your cone is free. I'm all for free ice cream! How many free cones might the shop give away? Or in other words, how many different ways can one choose 3 different flavors from the 6 flavor options? The counting formula tells us that C(6, 3) = 20, meaning there are 20 distinct triple-scoop cones.

The file combinations.cpp contains this function that counts combinations using the above formula:

int comboFormula(int n, int k)
{
    return factorial(n)/(factorial(k) * factorial(n-k));
}

There is a neat recursive insight that gives rise to an alternate means to count the number of combinations that is much more intuitive than a wacky formula.

In the diagram below, each dot represent one of the options in a set of size N. The goal is to count the ways to choose K items from the set.

Imagine dividing these N elements into one "selected" element that is currently under consideration and the N-1 others. The diagram below colors the selected element red and imagines a line between it and the rest.

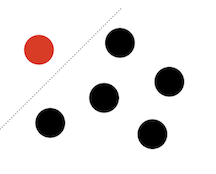
The red dot is being considered for inclusion in the combo of size-K. There are two possibilities for the red dot: we can include it as one of the chosen K or we can pass on it. If the red dot is among the chosen, we will then go on to count the ways we can choose K-1 elements from the N-1 remaining. If the red dot is not among the chosen, we go on to count how many ways can we choose K elements from the N-1 remaining. Summing those two counts together gives the total count of ways to choose K from N. Neat!

In the analogy of the ice cream shop, imagine considering the flavor chocolate. We count the number of triple-scoop cones that include a scoop of chocolate (choosing the additional two scoops from the remaining flavors) and add the count of cones that don't include chocolate (choosing three scoops from the remaining flavors). In this way, we count all possible combinations: those that include chocolate and those that don't.

Gathering the two counts from the remaining choices forms the recursive step in the algorithm. To complete the algorithm, you also need to identify the base case(s). Consider: for what values of n and k do you no longer have any further choices to recursively explore?

Write the function

int countCombos(int n, int k)

that uses the above recursive strategy to count the combinations.

Testing

You can test your countCombos function by comparing it to the provided comboFormula function. Add student test cases that call countCombos and comboFormula on the same values n and k and use EXPECT_EQUAL on the two function results.

Because comboFormula depends on factorial and the factorial of relatively small numbers is so large that it overflows the range of the int type, you will have to limit test inputs to values of n and k under 12. But your recursive version does not have the same limitation and is capable of correctly counting the combinations for much higher values of n and k. How might you construct a different kind of unit test for these values that does not rely on the use of comboFormula? (Random thought: Python allows for integer values of a much larger range than C++, coding a version of comboFormula in python would succeed and you could copy those values back to your C++ program. Hmm! )

For certain pairings of n and k, a call to comboFormula(n,k) should raise an error. (This is assuming you fixed factorial's handling of negative inputs during the warmup exercise) These values of n and k correspond to counting combinations which are impossible to form, such as attempting to choose 10 things from a set of size 9, attempting to choose a negative amount of things, or attempting to choose from a negative amount of options. Be sure that your countCombos also raises an error on such inputs.

Notes

• The countCombos function must operate recursively. There should be no loops, no multiplication, no calls to factorial.
• The countCombos function must not use any auxiliary data structures (no Stacks, Queues, Vectors, etc.)
• We have provided a few tests to get you started. You will need to add student tests of your own for complete coverage.

Extensions

The recursive insight used to count combinations also lends itself to constructing all of the possible combinations, instead of just counting them. Try your hand at writing the function choose that is given a Set of n options and count k, and fills the pass-by reference argument combos with all of the combos of size k drawn from the options set.

void choose(Set<int> options, int k, Set<Set<int>>& combos, 
                               Set<int> sofar = {} )

The choose function follows a similar recursive decomposition to countCombos. At each step of the recursion, it explores including the selected element into the current combo as well as not including it. The choose function tracks the current combo membership in a Set called sofar. When making the recursive calls, one call passes the sofar unchanged (having chosen to not add the selected element), the other call passes an updated sofar after having added the selected element. The set soFar will begin as an empty set and grow to contain all of the K chosen elements in the current combo.