Assign3: Sierpinski
Recursion can create incredible graphic designs of images that have self-similar subparts (also known as fractals). One of the most famous fractals is the Sierpinski triangle, named after the Polish mathematician Waclaw Sierpinski (1882–1969).
As with many self-similar images and fractal patterns, it is defined recursively:
- An order-0 Sierpinski triangle is a plain filled triangle.
- An order-n Sierpinski triangle, where n > 0, consists of three Sierpinski triangles of order n – 1, each half as large as the main triangle, arranged so that they meet corner-to-corner.
For example, here are Sierpinski triangles of the first few orders:

Take a moment to confirm that the order-1 Sierpinski triangle indeed consists of three smaller copies of the order-0 Sierpinski triangle, that the order-2 Sierpinski triangle is formed from three smaller copies of the order-1 Sierpinski triangle, and so on.
As a note, although it might look like we’re drawing a single black triangle with a lot of white triangles inside it, that’s actually not the case. Every triangle drawn here is black; the white triangles represent places where no triangle was drawn.
Your task is to implement the function
void drawSierpinskiTriangle(GWindow& window, GPoint one, GPoint two, GPoint three, int order)
that takes as input the three corner points of a triangle and the order. The function draws a Sierpinski triangle defined by those three corner points and of the specified order into the given window.
We provide the fillBlackTriangle helper function to fill a triangle defined by its three corner points:
void fillBlackTriangle(GWindow& window, GPoint one, GPoint two, GPoint three)
Testing graphics
A function that produces graphical output, such as Sierpinski, doesn't lend itself to being unit-tested, so we provide a simple GUI you can use to interactively test your drawing. You can run the GUI with a call to the runDemos() function. Our starter code calls runDemos from the single "unit test" for the Sierpinski file. Here is a screencast that demonstrates using the GUI on Sierpinski.
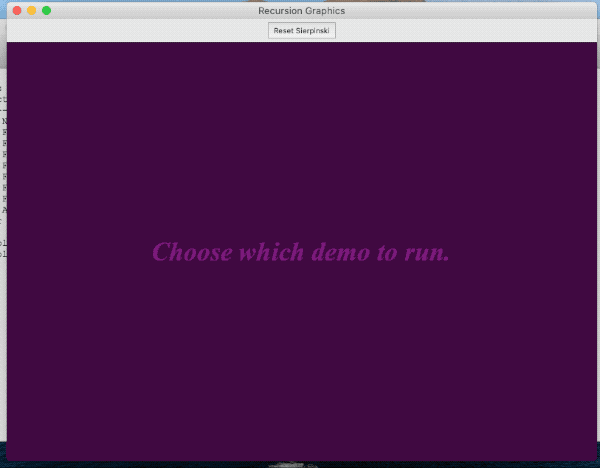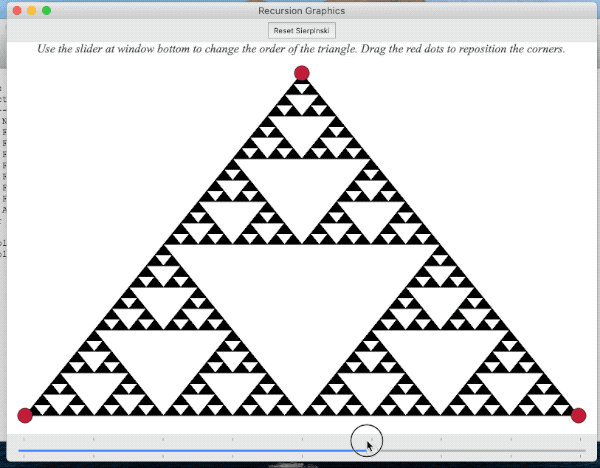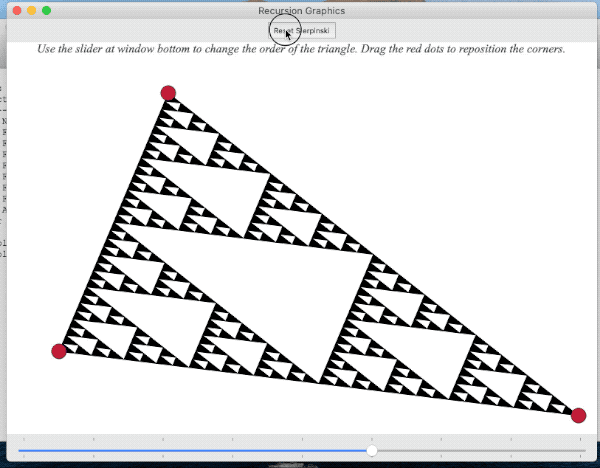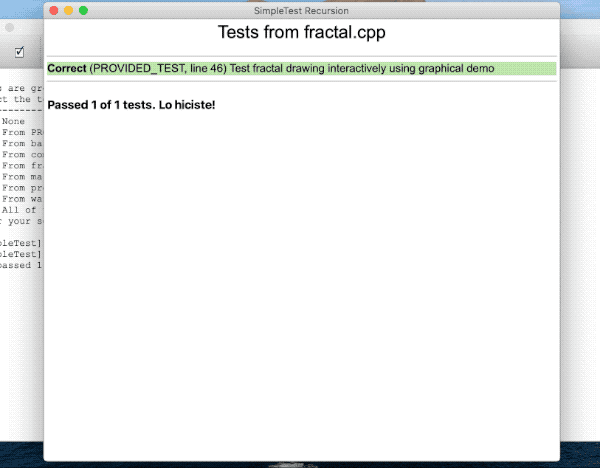
In the GUI, use the slider to change the order and drag the corners to change the triangle dimensions. Visually inspect the drawing for correctness. When are you done testing, simply close the window to exit the GUI.
Q8: Without automated unit tests, you need to develop new techniques for test coverage. What were the strategies you used for testing Sierpinski?
Notes
-
Draw pictures! One key part is figuring out where each triangle’s corners are, and that’s easier to do with a diagram in front of you.
-
The midpoint of each side of the large outer triangle becomes a corner of the smaller inner triangles. Given a line segment whose endpoints are
{x1, y1}and{x2, y2}, its midpoint is at{ (x1+x2)/2, (y1+y2)/2 }. -
The three corner points of the triangle don’t necessarily have to form an equilateral triangle or be parallel to the base or side of the window. There isn’t any particular ordering to which corner is identified as
oneversustwoversusthree. -
You should only draw the black triangles that make up the Sierpinski triangle. The white parts of the triangle are, in a sense, “negative space;” they’re the regions where nothing is drawn.
-
The only function you should call to draw things in the window is
fillBlackTriangle, mentioned above. You do not need to dig into any other drawing functionality in the Stanford libraries.
Extensions
The Sierpinski triangle is only one of many self-similar images; consider coding up another! We’d love to see what you create.
Some resources: