Assign4: Merge

Binary merge

The binary merge operation is a very common operation in computer science, where two individual sorted sequences are merged into one larger sorted sequence. This operation serves as the backbone of many different sorting algorithms (some of which we will explore later in the course), which themselves are used in a broad diversity of programs and applications. In that way, the binary merge is the hardworking worker bee at the core of many interesting algorithms and applications!

Your first task is to write the function

Queue<int> merge(Queue<int> one, Queue<int> two)

that performs a binary merge.

Timing and Big O

We have added a new TIME_OPERATION(size, expression) feature to the SimpleTest framework. it allows you to do simple execution timing. It can be used like this:

PROVIDED_TEST("Time operation vector sort")
{
    Vector<int> v = {3, 7, 2, 45, 2, 6, 3, 56, 12};
    TIME_OPERATION(v.size(), v.sort());
}

The test results for this test will include the measured time of execution:

Time operation vector sort
    Line 174 Time v.sort() (size =       9) completed in        0 secs

Timing the same operation over a range of input sizes measures the growth of the work relative to input size, i.e. the algorithm's Big O. Handy!

First predict what you expect to be the Big O of your merge function. Then use the timing operation to measure the execution time over 4 or more different sizes. For small input, the timing data is very noisy, for large inputs, it requires much patience. Experiment to find sizes in the "sweet spot" – large enough to be fairly stable but small enough to complete under a minute.

In short_answer.txt:

Multiway merge

A multiway merge or k-way merge is an extension of the binary merge operation, which receives k sorted lists and merges the lists into a single sorted list.

We have provided in the starter code a version of multiMerge that is built on top of your binary merge. The function is also replicated below for convenience.

Queue<int> multiMerge(Vector<Queue<int>>& all)
{
    Queue<int> result;

    for (Queue<int> q : all) {
        result = merge(q, result);
    }
    return result;
}

Divide and conquer to the rescue

The above implementation of multiMerge really slows down for longer sequences, since the merge operation is repeatedly applied to longer and longer sequences.

Your goal now is to write the function

Queue<int> recMultiMerge(Vector<Queue<int>>& all)

that applies the power of recursive divide-and-conquer to achieve much improved performance for multiway merge.

The strategy for recMultiMerge is as follows:

  1. Divide the input collection of k sequences into two halves. The "left" half is the first K/2 sequences in the vector, and the "right" half is the rest of the sequences.
    • The Vector subList operation can be used to subdivide a Vector, which you may find helpful.
  2. Make a recursive call to recMultiMerge on the "left" half of the sequences to generate one combined, sorted sequence. Then, do the same for the "right" half of the sequences, generating a second combined, sorted sequence.
  3. Use your binary merge function to join the two combined sequences into the final result sequence, which is then returned.

In the diagram below, we drew the contents of each queue in a vertical yellow box. The initial collection has seven sequences. The dotted line shows the division into left and right halves of 3 and 4 sequences, respectively. Each half is recursively multiway merged. The combine step calls binary merge to produce the final result.

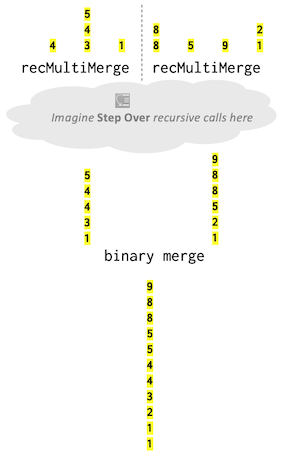
Example merge from bottom up

You can prove that the runtime for recMultiMerge is O(n log k) where n is the total number of elements over all sequences and k is the count of sequences at the start of the multiway merge.

What, exactly, does O(n log k) mean? It might help to imagine that nis allowed to vary, while k stays constant. If you have a small value of k, then log k is also small, and as n varies you’ll get a plot of a straight line with a small slope.

If you were to increase the value k, the slope of that line will gently to increase, but not by much because log k grows extremely slowly. In particular, if you look at values of k that grow exponentially quickly (say, k = 1, then 4, then 16, then 64, then 256), the slope of the lines increase by some fixed rate.

Given an input of n elements that is entirely unsorted, we could place each element in its own sequence and call recMultiMerge on that collection of n sequences. This would make k equal to n (maximal possible value for k). The operation would run in time O(n log n). The classic mergesort algorithm uses an approach similar to this. (more on that coming up when we discuss sorting and Big O).

The elements that are already arranged in sorted sequences give a jump start to the process. The smaller the value of k, the more work has already been done and the quicker the whole process can complete. For example, if n is a million and k is 10, O(n log k) runs about 5 times faster then O(n log n).

To finish off this task:

Notes