Introduction to Linked Lists
CS 106B: Programming Abstractions
Spring 2023, Stanford University Computer Science Department
Lecturer: Chris Gregg, Head CA: Neel Kishnani

Slide 2
Announcements
- Assignment 5 is due Friday
Slide 3
Today's Topics
- Structs and pointers
- Can you architect a queue?
- Let's do it with a Vector
- Let's try it with links
- Introduction to the Linked List data structure
- The Node
struct
- The Node
- Lord of the Linked Lists
- How is the Stack implemented with a linked list?
- Linked List Queue implementation
Slide 4
Using pointers with class and struct objects
- Let's define a class (or it could be a struct) as follows:
class Date { public: int day; int month; int year; string dayOfWeek; int daysInMonth(); }; - Pointers can point to a class or struct just like they can to any other variable:
Date* dPtr = new Date; // we now have a pointer to a Date object - If we want to access the class variables and functions, we could do this:
(*dPtr).day = 7; int numDays = (*dPtr).daysInMonth(); cout << (*dPtr).month << endl; - But, this notation is cumbersome, and the parentheses are necessary becasue the "dot" has a higher precedence than the
*. - So, there is a different, more intuitive syntax, called the arrow syntax:
->dPtr->day = 7; int numDays = dPtr->daysInMonth(); cout << dPtr->month << endl; - Arrow notation,
x->varis equivalent to(*x).var, and we will use it exclusively when using classes and structs.
Slide 5
Can you architect a queue?
- Let's investigate building a queue from a Vector
- The following class definition for an integer queue would suffice for the
enqueueanddequeuefunctions, with aVectorholding the data.class QueueInt { // in QueueInt.h public: QueueInt (); // constructor void enqueue(int value); // append a value int dequeue(); // return the first-in value private: Vector<int> data; // member variables }; - Let's assume that we have the back of the queue on the left, and the front of the queue on the right. If we enqueue eight values, the vector would look like this:
back front ↓ ↓ 1 2 3 4 5 6 7 8 - The
dequeueoperation is relatively straightforward: we just remove and return the element from the end, and the front is now at the previous index:back front ↓ ↓ 1 2 3 4 5 6 7 _ - But,
enqueueis more involved. Because the back is on the left of the vector, we have to move all the elements over one, one at at time before placing our value into the vector. If weenqueue(9)on the vector, this is what happens:1 2 3 4 5 6 7 7 1 2 3 4 5 6 6 7 1 2 3 4 5 5 6 7 1 2 3 4 4 5 6 7 1 2 3 3 4 5 6 7 1 2 2 3 4 5 6 7 1 1 2 3 4 5 6 7 9 1 2 3 4 5 6 7
- If we look at the complexity of
enqueue()anddequeue(), we have:enqueue: O(n)dequeue: O(1)

Slide 6
And Now for Something Completely Different
- Let's use pointers to make things a bit more interesting.
-
Let's say that we have an 8 that we want to put into a queue. We can make a variable that holds an 8, and let's say we do this with dynamic memory.

- Now, let's say we have a
datapointer that points to an integer. In this case, it will point to the 8. We now have a queue! The front of the queue is the 8, as is the back of the queue.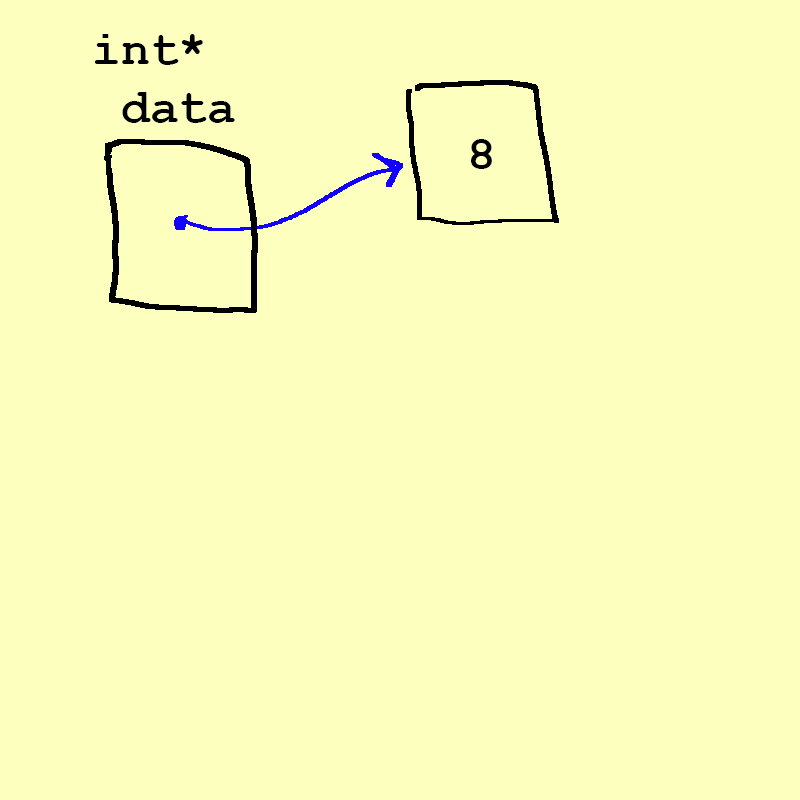
- Now, what if we want to
enqueue(7)into the queue? Well, we can create a 7 just like we created the 8.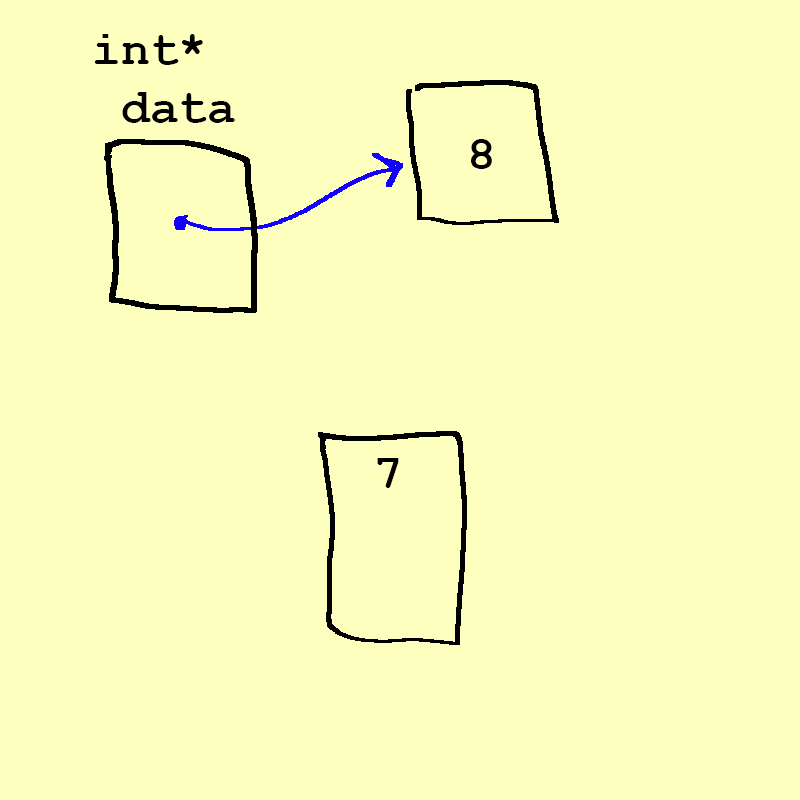
-
What if we simply put a
7somewhere in memory, and then changeddatato point to the7, and made the7(somewhow) point to the8? (The somehow, by the way, is a pointer that is associated with the7called itsnextpointer, in astruct– we will get to that!).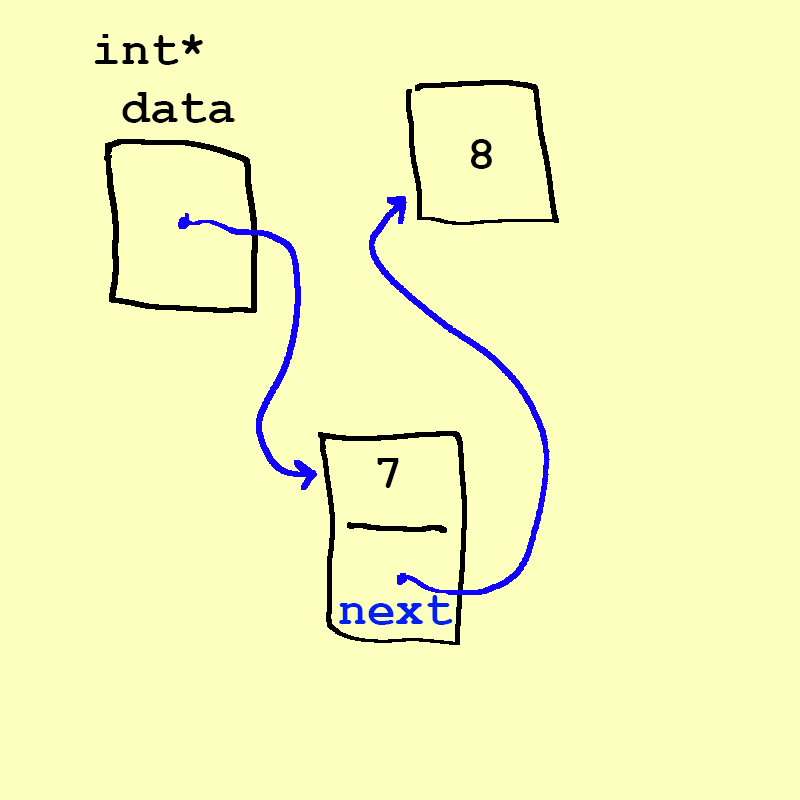
- Now we have enqueued the 7 into the back of the queue! Our data points to the 7, which we have "pointed" to the 8.
- Let's
enqueue(6), and go through the process a bit slower.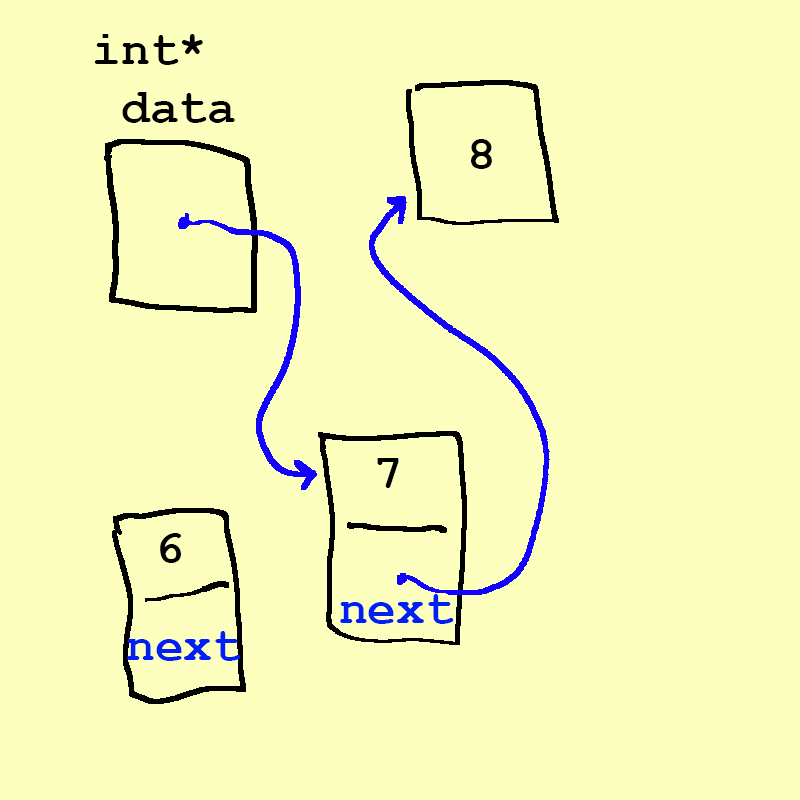
-
Now we have a
6in memory, but not yet connected to anything. We must getdatato point to the 6, and then have the 6 point to the 7. We actually first point the 6 to the 7. It turns out that if we didn't do that, It turns out that we have to do it in this order becuase if we changed data first, we would lose access to the 7, becuase data was the only thing pointing to the 7 (we'll cover this soon!)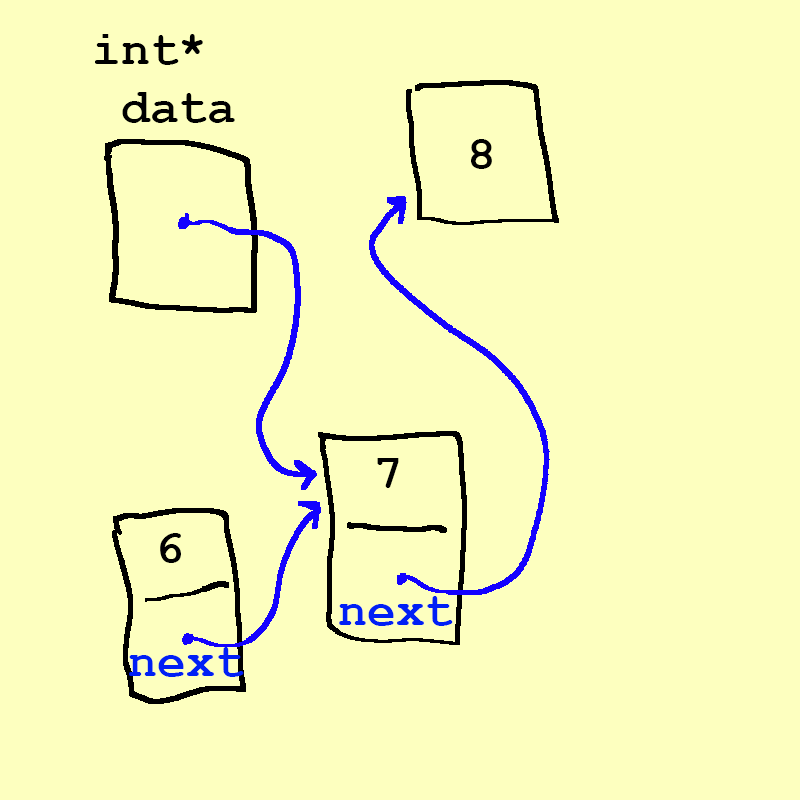
- Remember, two pointers can point to the same value (in this case, both
dataand the6pointer). -
Next, we can change data to point to the 6:
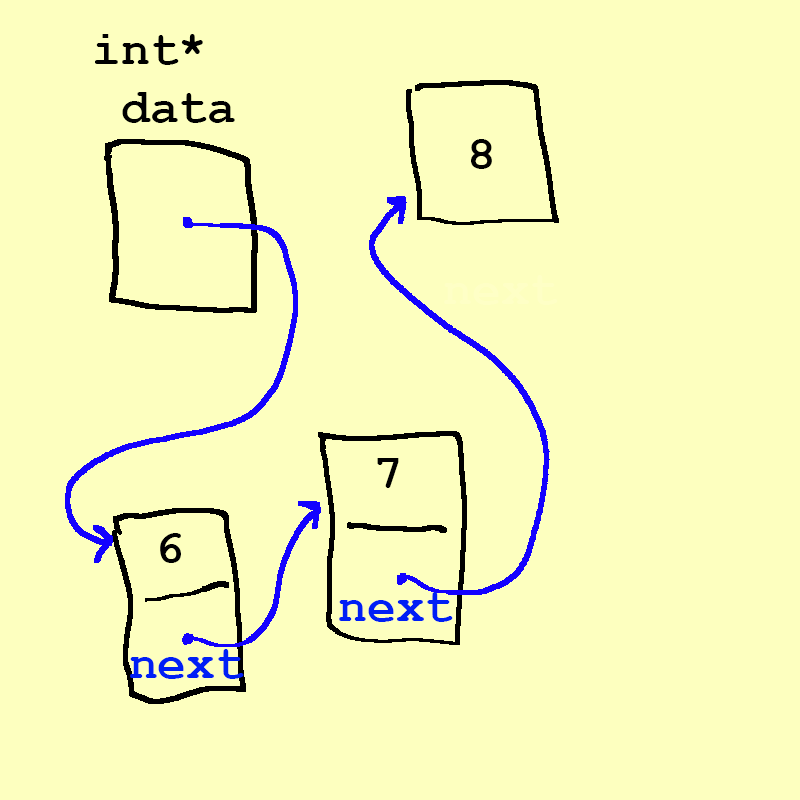
- Oh, look, we've enqueued the
6! - There are two bits of extra information that we need to make this list a proper queue
- We need to figure out what 8 points to. In this case, we will point 8 to
nullptr, indicating that it is the end of the list. If we check 8's pointer and find that it isnullptr, then we are at the end of the list (or, in this case, the front of the queue). In the diagram, we just represent this with a slash through 8's pointer region. - We need to designate the front as such, and the back as such:
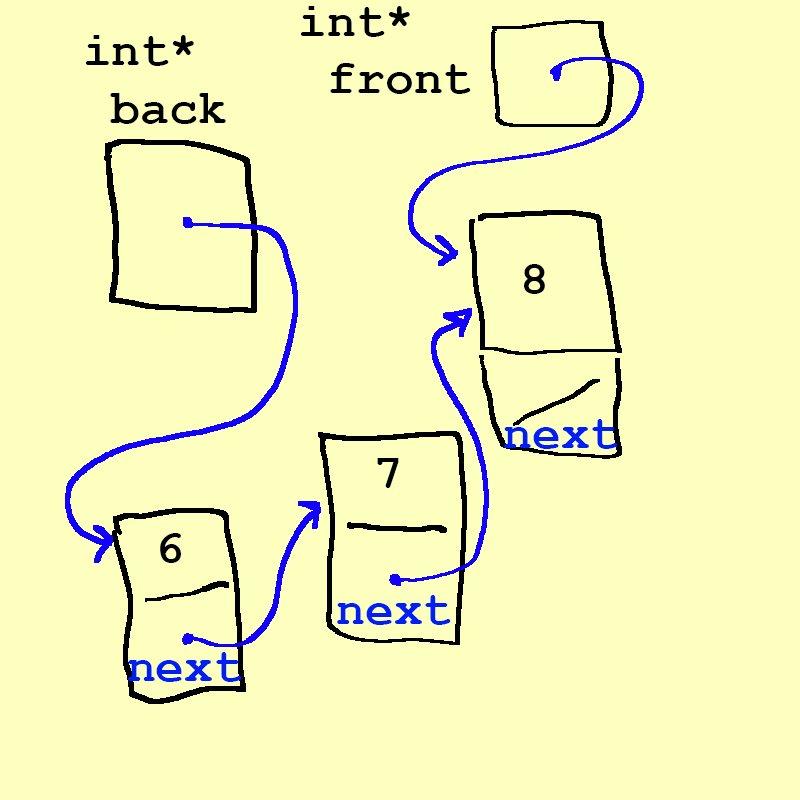
- We need to figure out what 8 points to. In this case, we will point 8 to
- It turns out that this is the wrong way to build a queue with a linked list! We'll see at the end of the lecture a better way to do it by changing things just a bit.
Slide 7
Linked Lists
- What we've just examined is the beginning of a linked list
- A linked list is a chain of nodes
- Each node contains two pieces of information:
- Some piece of data that is stored in the sequence
- A link to the next node in the list
- We can traverse the list by starting at the first node and repeatedly following its link.
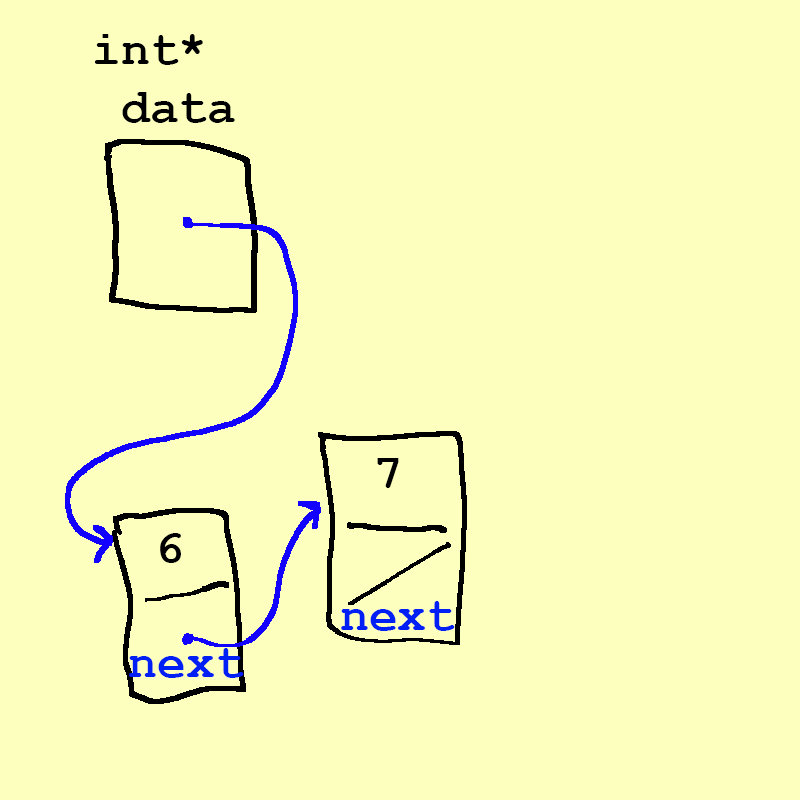
- Each element is stored separately from the rest.
- The elements are then chained together into a sequence.
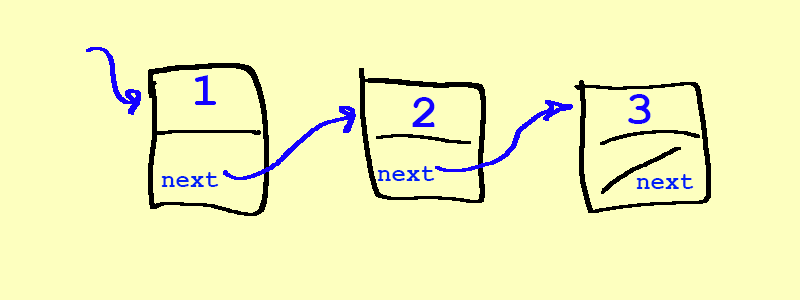
- To add a node at the end, we chain the last element to the end, by first finding the end (traversing the list), and then adding it:
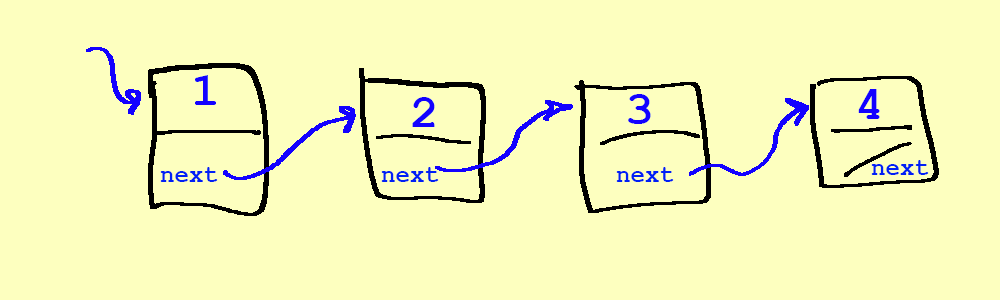
Slide 8
Adding a node in the middle of a linked list
- To insert a node into the middle of a linked list, we first need to find the location where we are adding it – this can be a slow process because we have to travers from the beginning!
- Let's say we want to insert between 2 and 3. First, we need to find 2 by traversing from 1, and then we split the list and insert our new element:
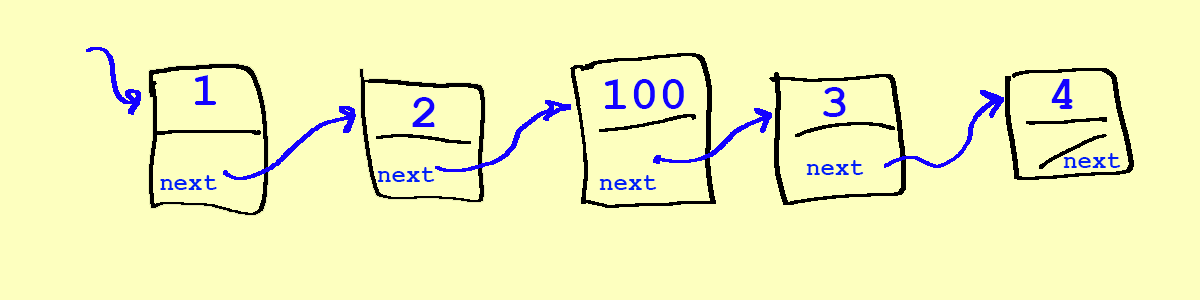
Slide 9
Removing a node in the middle of a linked list
- To remove a node into the middle of a linked list, we first need to find the location where we are adding it, as with insert.
- Let's say we want to remove 3. First, we need to find 100 by traversing from 1, then 2, and then to 100. Then, we rewire the list so 100 points to 4:
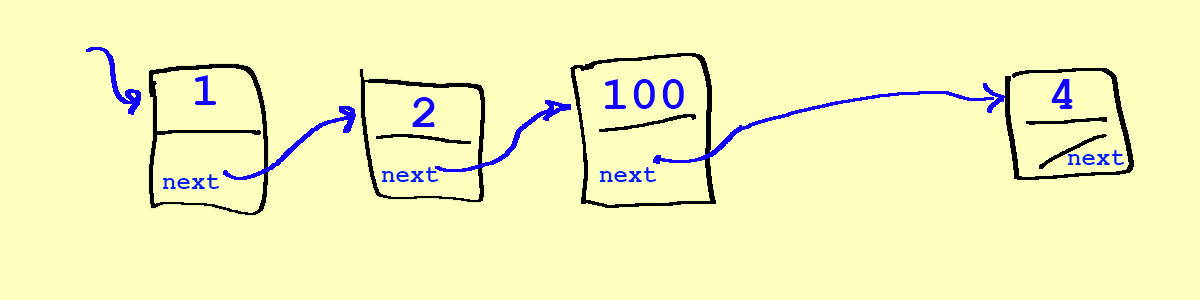
Slide 10
Why linked lists?
- We can efficiently splice new elements into the list or remove existing elements anywhere in the list
- We never have to do a massive copy step
- Linked lists have many tradeoffs, and are not often the best data structure!
Slide 11
Linked lists in C++
- Let's take a look at building a linked list of strings
- In C++, we represent the node in the linked list as a
struct, with two fields, adatafield, and anextfield:struct Node { string data; /* ? */ next; - But, what is the type of next? It must point to another
Node, so…it is aNode*type:struct Node { string data; Node* next; }; - The structure is defined recursively! The compiler can handle the fact that in the definition of the
Nodethere is aNode*, becuase it knows it is simply a pointer. We could not recursively define theNodewith an actualNodeobject inside thestruct, as that would be impossible to realize.
Slide 12
Always!
Always draw pictures when you are building linked lists! This is critical to getting the hang of it.
Slide 13
Lord of the Linked Lists
- In a scene that was brilliantly captured in Peter Jackson’s film adaptation of The Return of the King, Rohan is alerted to the danger to Gondor by a succession of signal fires moving from mountain top to mountain top. This scene is a perfect illustration of the idea of message passing in a linked list.

Slide 14
Return of the King

Slide 15
Lord of the Linked Lists
- We are going to make a San Francisco-based linked list, based on CalTrain stops. Step 1, make the linked list:
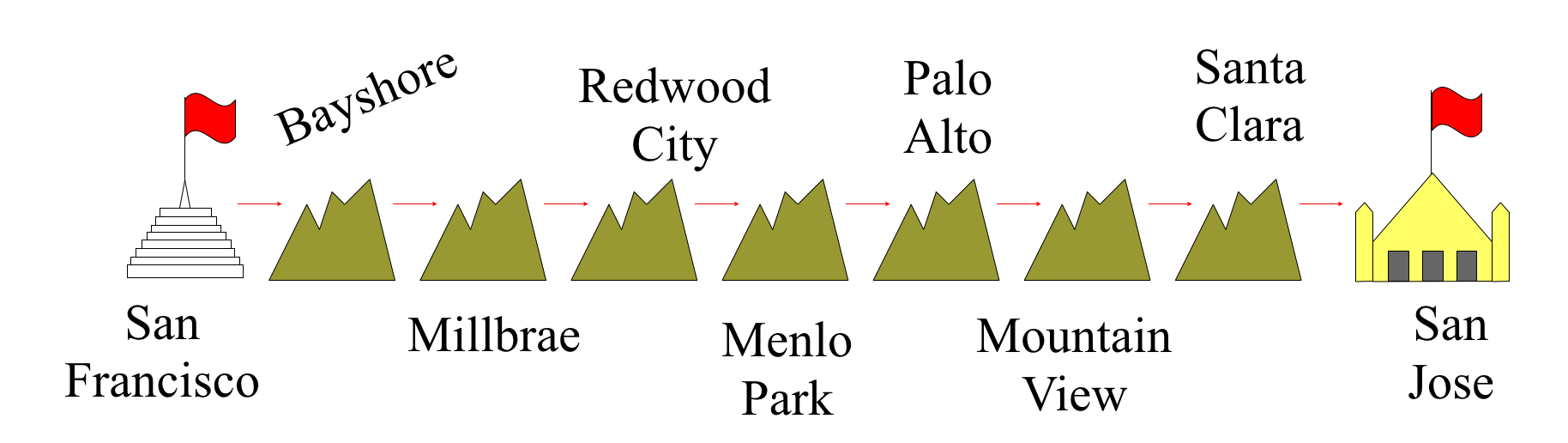
- Step 2: Light the fires!
struct Tower { string name; /* The name of this tower */ Tower* next; /* Pointer to the next tower */ }; - Add the first tower:
// add the first tower Tower * head = new Tower; head->name = "San Jose"; head->next = nullptr; - The
mainfunction:// main Tower * head = new Tower; head->name = "San Jose"; head->next = nullptr; head = createTower("Santa Clara", head); head = createTower("Mountain View", head); head = createTower("Palo Alto", head); head = createTower("Menlo Park", head); head = createTower("Redwood City", head); head = createTower("Millbrae", head); head = createTower("Bayshore", head); head = createTower("San Francisco", head); - The
createTowerfunction:Tower* createTower(string name, Tower *next) { Tower* tp = new Tower; tp->name = name; tp->next = next; return tp; } - The
signalfunction (which is recursive!):void signal(Tower* start) { if (start != nullptr) { cout << "Lighting " << start->name << endl; signal(start->next); } } - We call the function with the
head:signal(head); - By the way: the
headpointer is not aTower! it is only a pointer to aTower, and the firstToweris San Francisco.
Slide 16
How is the Stack implemented with a linked list?

- The Node definition we've seen before:
struct Node { int data; Node *next; };
Slide 17
Stack
- Let's assume we have the following stack already, with 8 at the top, and 9 below 8. We then want to
push(7)onto the stack: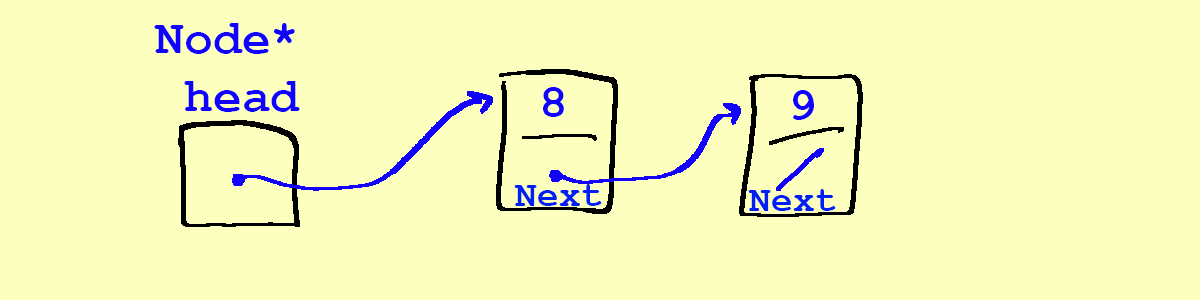
- Here is our goal:
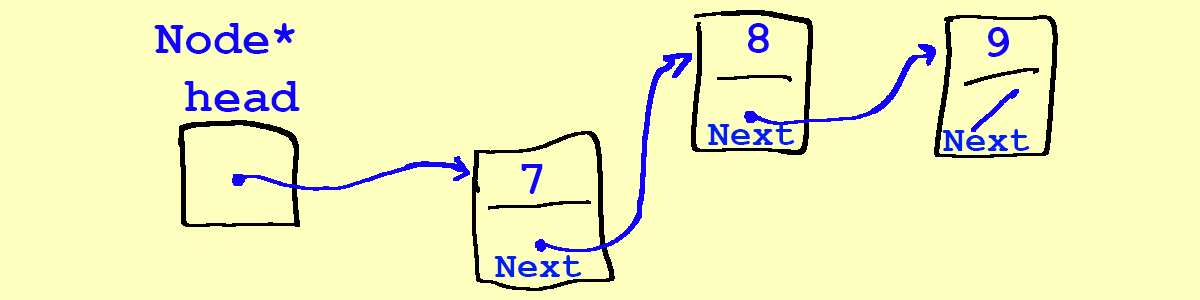
- Our first attempt at
push(7):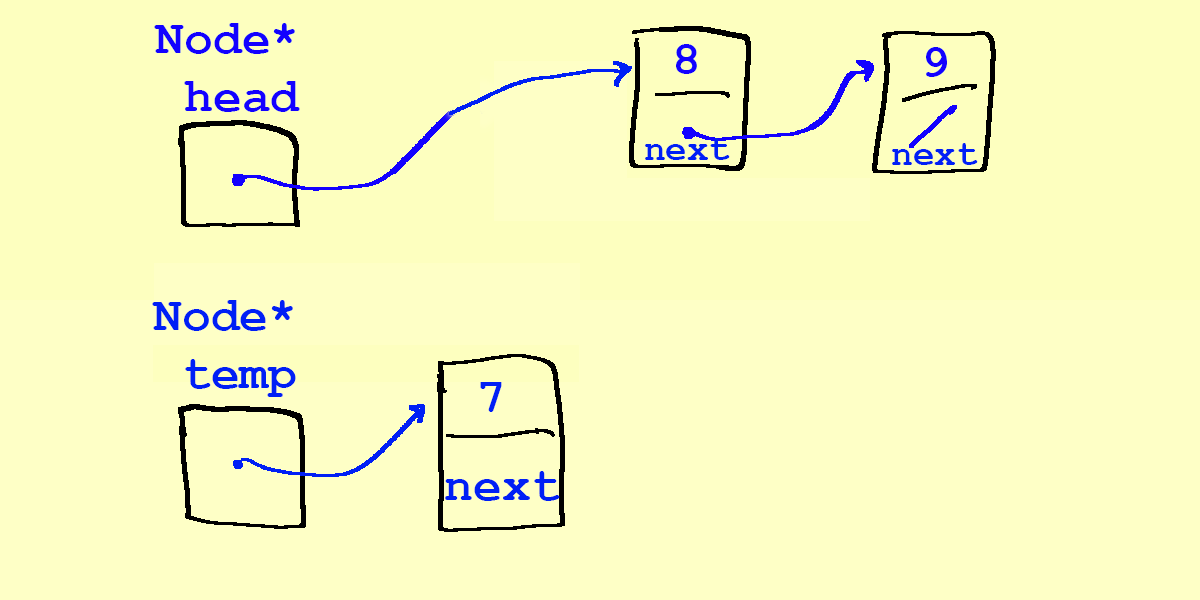
Node* temp = new Node; temp->data = 7; - If we try to rewire by changing
headfirst…head = temp;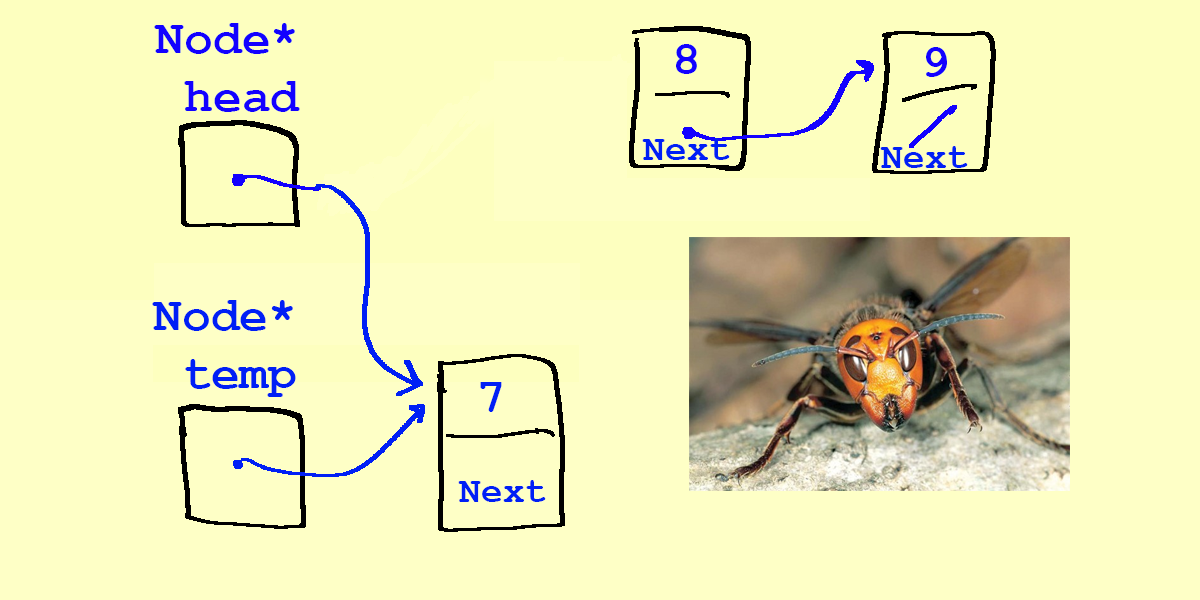
- In other words: a linked list's elements must be pointed to, because we need to keep track of them. In our attempt above, we've lost access to the 8, becuase the only thing pointing at the 8 was
head. If we reassignheadto point to another object (the 7 in this case), we've broken the chain and lost 8. This is a common bug! - Let's try again:

- Here is our goal:

- Our next attempt at
push(7):
Node* temp = new Node; temp->data = 7; - Now we rewire 7's
nextpointer first:temp->next = head;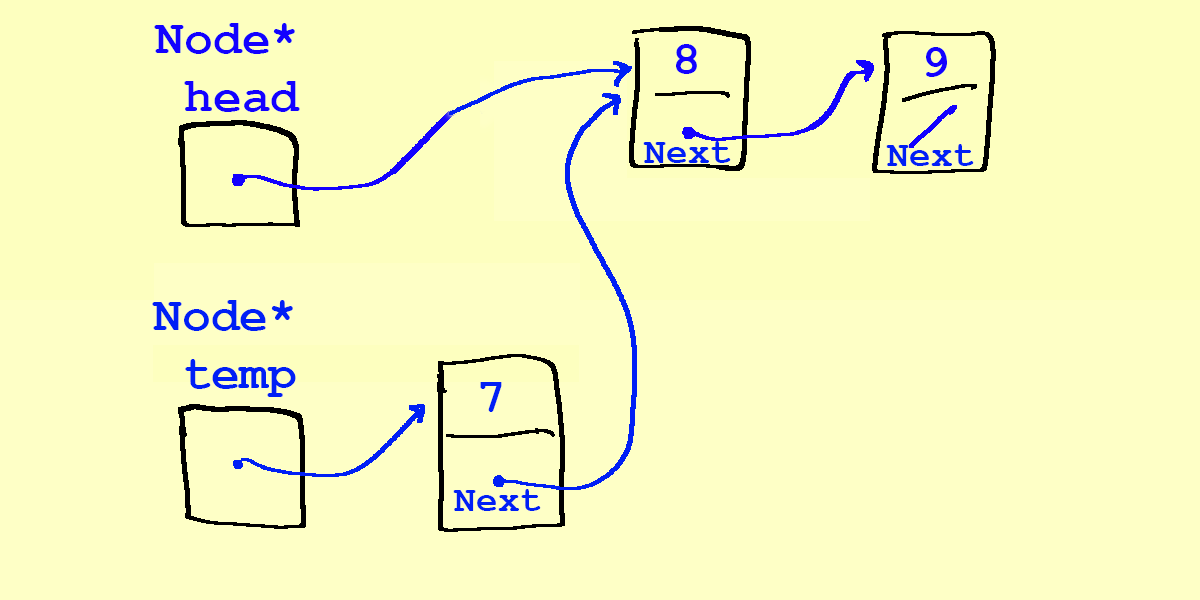
- You might be thinking, wait – why didn't the arrow go from the 7 to the head? – this is a common misconception of what is happening!
- Remember,
headis not aNode.headis a pointer to aNode. Notice thatheaddoes not have anext– it's not an object, just a pointer. - The statement
temp->next = head;says, "give 7's next pointer the same data as head", which is what we want to do.
- Remember,
- Now, we are able to reassign
headto point to the 7, and we will have a correct linked list with 7 pushed onto the top: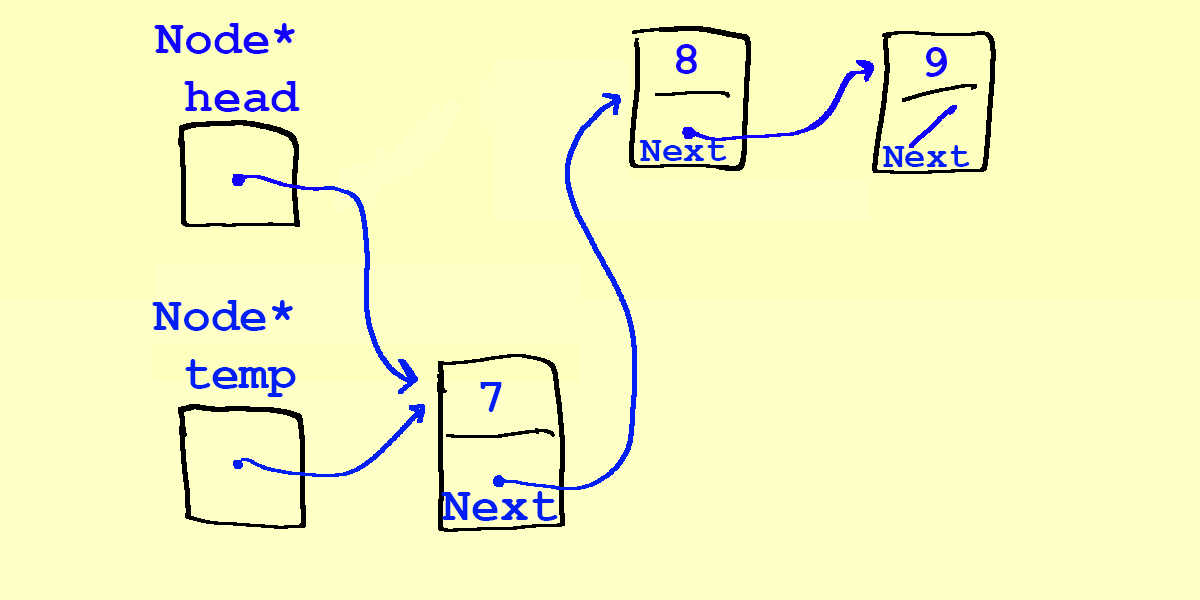
- Our
temppointer actually disappears when thepushoperation is complete (it goes out of scope), so we are left with the following: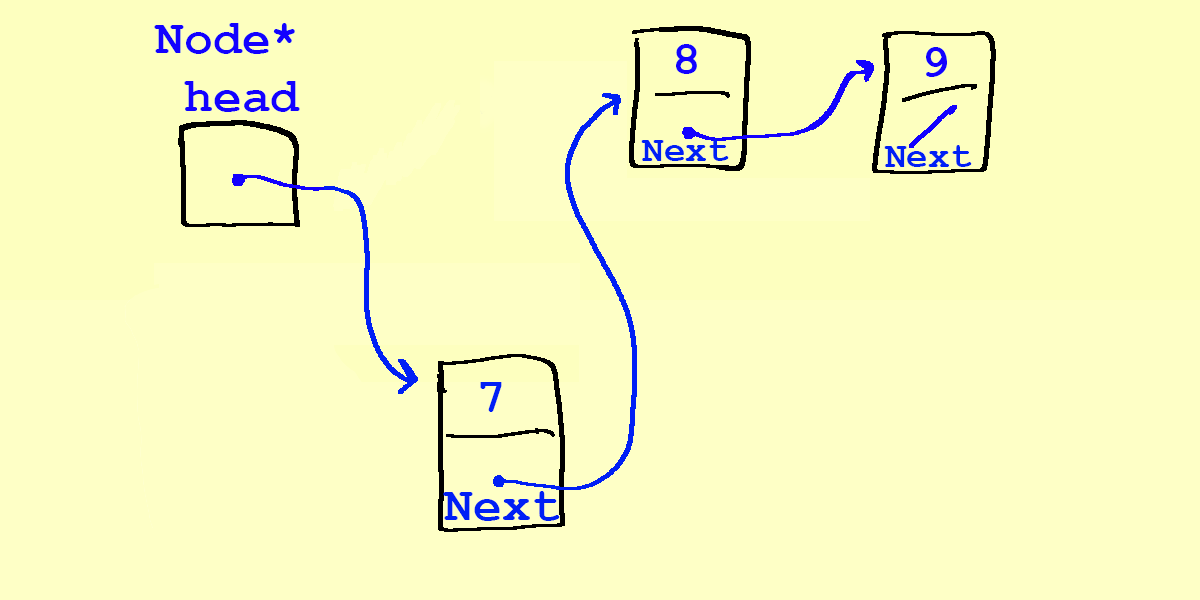
Slide 18
Stack pop()
- To pop a data from our stack, we start like this:
int toReturn = head->data;
- What if we tried this to reassign
head?head = head->next;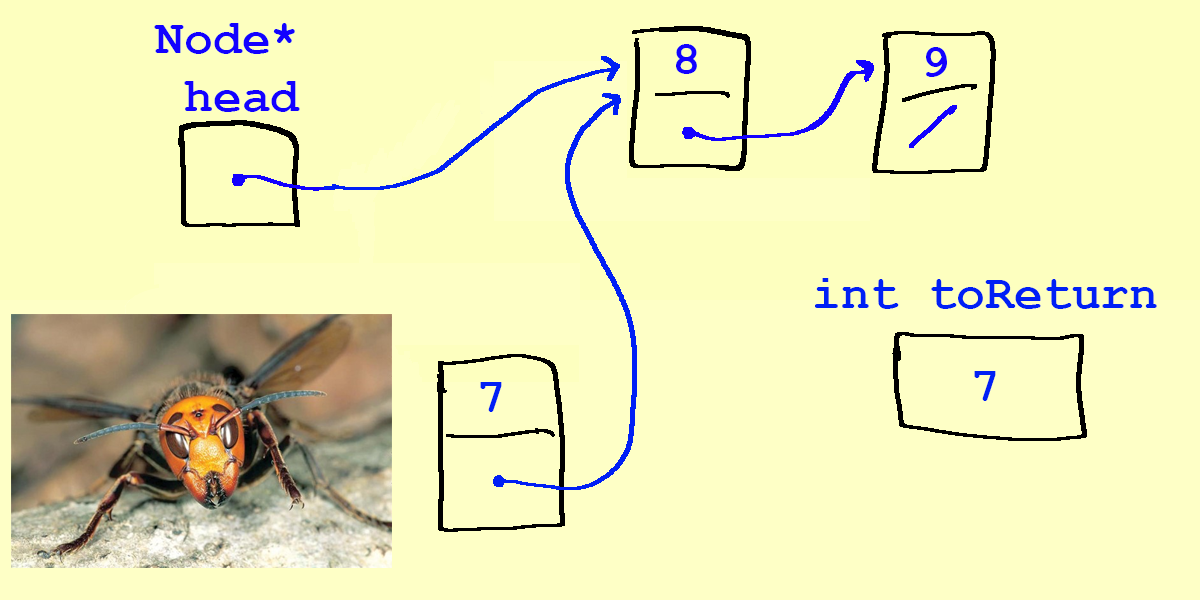
- This is a bug! Our linked list is fine, but we have a memory leak! We have left the 7 in memory and not returned it to the operating system with
delete. - Instead, we need to do this:
Node* temp = head;
- Now we can reassign
head:head = head->next;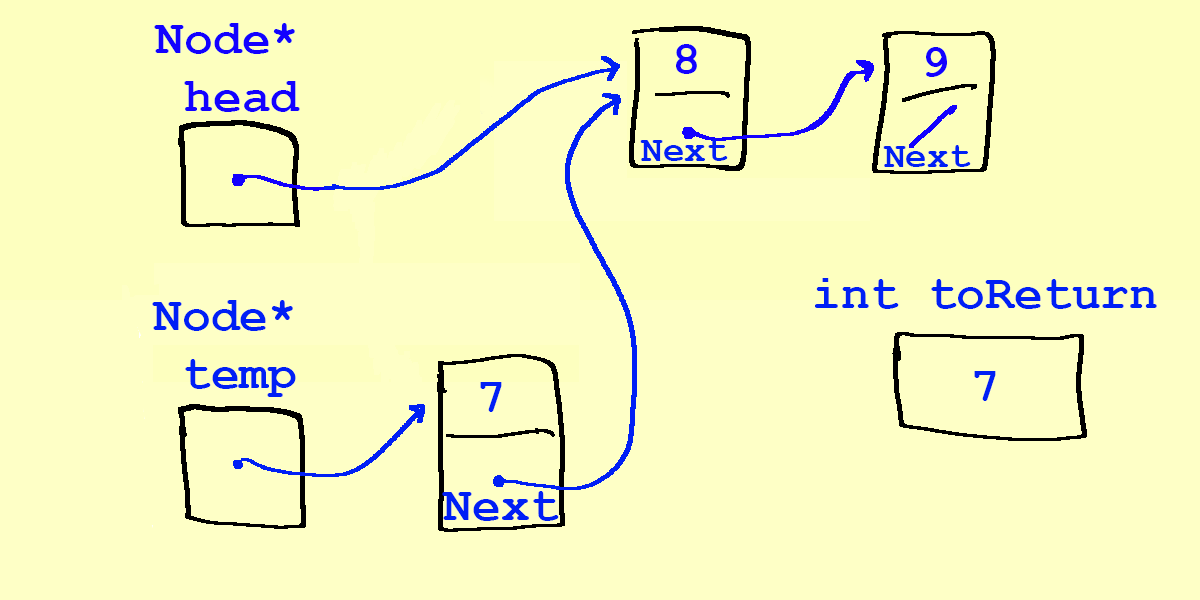
- Because we still have access to the 7, we can return the memory to the operating system:
delete temp;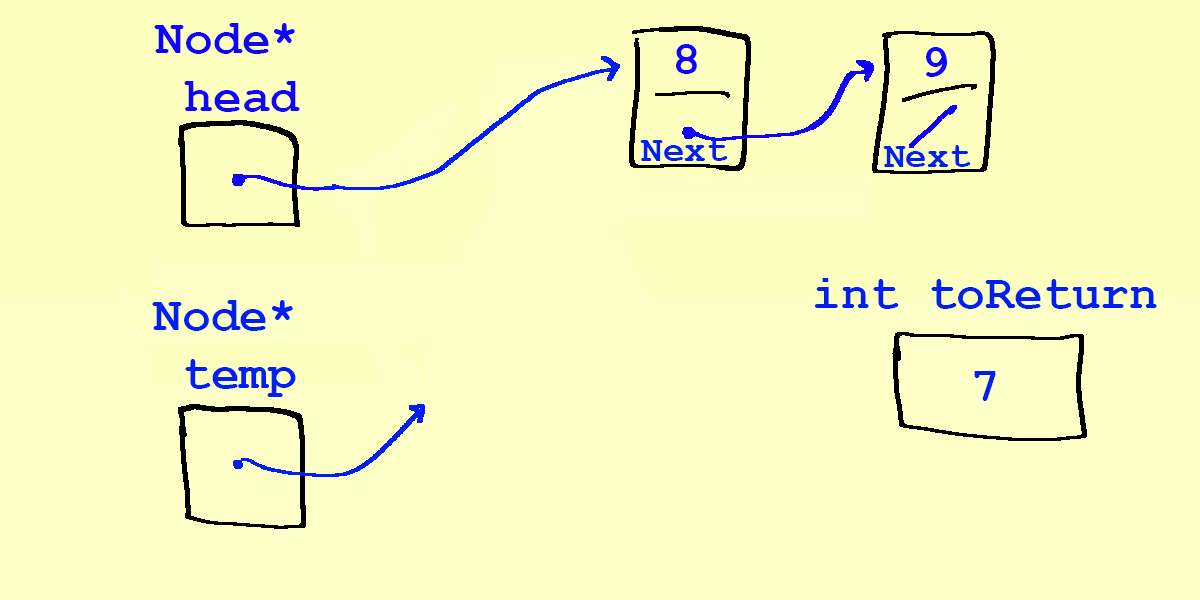
- Finally, we return the data, and
tempgoes out of scope:return toReturn;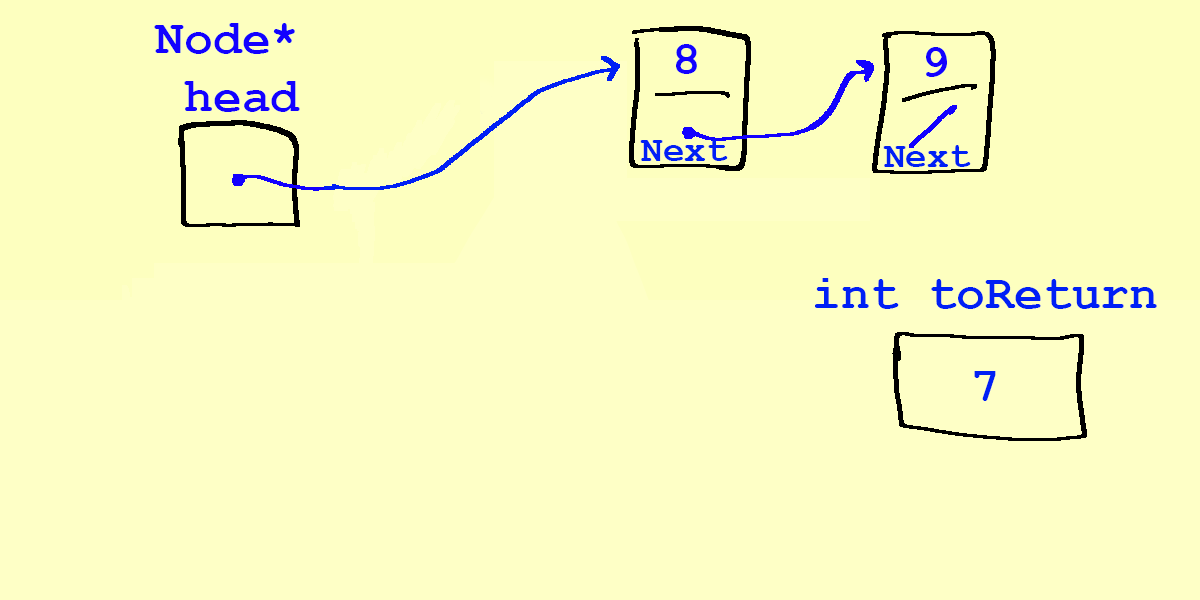
Slide 19
Stack Code
- Header,
intStack.h:
#pragma once
class IntStack {
public:
IntStack(); // constructor
~IntStack();
bool isEmpty();
void push(int value);
int top();
int pop();
private:
struct Node {
int data;
Node* next;
};
Node* head;
};
- Class code,
intStack.cpp
#include "intStack.h"
IntStack::IntStack()
{
head = nullptr;
}
IntStack::~IntStack()
{
while (head != nullptr) {
Node *temp = head;
head = head->next;
delete temp;
}
}
void IntStack::push(int value)
{
Node* node = new Node;
node->data = value;
node->next = head;
head = node;
}
int IntStack::pop()
{
if (isEmpty()) {
throw "Error! Trying to pop from empty stack!";
}
int toReturn = head->data;
Node* temp = head;
head = head->next;
delete temp;
return toReturn;
}
Slide 20
A Better Linked List Queue
- At the beginning of this topic, we discussed how to build a queue with a linked list. We had the back as the first element in the list, and the front as the second element. This led to O(1) behavior for enqueue, and O(n) behavior for dequeue. We can do better!
- If we hold a pointer to the front and to the back, and we make the front the first element in the list, and the back the last element in the list, we can successfully make a queue with O(1) behavior for both enqueue and dequeue.
- Here is the code, then we'll walk through some examples:
intQueue.h
#pragma once
class IntQueue {
public:
IntQueue(); // constructor
~IntQueue();
bool isEmpty();
void enqueue(int value);
int front();
int dequeue();
private:
struct Node {
int data;
Node* next;
};
Node* _front;
Node* _back;
};
intQueue.cpp:
#include "intQueue.h"
IntQueue::IntQueue()
{
_front = nullptr;
_back = nullptr;
}
IntQueue::~IntQueue()
{
while (_front != nullptr) {
Node *temp = _front;
_front = _front->next;
delete temp;
}
}
void IntQueue::enqueue(int value)
{
Node* node = new Node;
node->data = value;
node->next = nullptr;
if (_back == nullptr) { // enqueue on empty queue
_front = node;
_back = node;
} else {
_back->next = node;
_back = node;
}
}
int IntQueue::dequeue()
{
if (isEmpty()) {
throw "Error! Trying to dequeue from empty queue!";
}
int toReturn = _front->data;
Node* temp = _front;
_front = _front->next;
if (_front == nullptr) {
_back = nullptr; // empty queue
}
delete temp;
return toReturn;
}
bool IntQueue::isEmpty()
{
return _front == nullptr;
}
int IntQueue::front()
{
return _front->data;
}