Stats 300B: Theory of Statistics II
Instructor
Professor John Duchi, Sequoia 126.
Office hours: by appointment, as we use the course lecture time as question-and-answer and examples.
Teaching Assistants
Maxime Cauchois
Office hours: Tuesdays, 5:30 - 7:30 PM. Zoom link on canvas.
Kevin Guo
Office hours: Wednesdays, 10 AM - 12 PM. Zoom link on canvas.
Prerequisites
Stats 300A, Stats 310A.
Course communication, questions
The course staff email address is stats300b-win2021-staff@lists.stanford.edu. Please do not use the instructor's or TAs’ direct email addresses for matters related to the course.
We will use Ed this quarter for answering questions, finding collaborators, and other course-related things. You should be able to sign up at this link, and use the following link for class discussion
Course Overview
In this class, we will cover classical and not-so-classical techniques underpinning asymptotic statistics and large sample theory. We will highlight a few of the big ideas, but the breadth of the subject by now is so large that our treatment will necessarily be spotty.
Outline
- Maximum likelihood estimation and models (2 weeks)
Basic M-estimators, Asymptotic normality via the central limit theorem (CLT), Taylor-like models, The
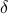 -method
-method- Testing (2 weeks)
Confidence intervals and
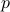 -values, Relative efficiency, Nonparametric tests, Worst-case alternatives
-values, Relative efficiency, Nonparametric tests, Worst-case alternatives- U-statistics (1 week)
Projections, Hoeffding and Hajek decompositions, One-sample and two-sample U-statistics, Degenerate U-statistics
- Convergence of general random variables, processes, and uniform laws (3 weeks)
Basic concentration inequalities, Uniform laws of large numbers and Glivenko Cantelli classes, Rademacher complexity, symmetrization, matrix concentration, Prohorov and Portmanteau theorems, Uniform central limit theorems
- Optimality, power, and contiguity (2 weeks)
Contiguity and absolute continuity, Local asymptotic normality and quadratic mean differentiability, Limiting normal experiments and asymptotic power, Local asymptotic minimax theorems, Super-efficienty and the Hodges phenomenon
Grading
Your grade will be determined by weekly problem sets (50%), and a weekly etude (50%). We reserve the right to change the relative weighting of these at any time.
There will be weekly homework assignments throughout the course, which will count for 50% of the grade. In effort to speed grading and homework return to you, we will grade homework problems and their sub-parts on a {0, 1, 2}-scale: 0 indicates a completely incorrect answer, 1 indicating approximately halfway correct, 2 indicating more or less correct. You are welcome to collaborate on these problem sets, but please acknowledge your collaborators.
There will be no final exam this quarter. Instead, each week there will be a single solo problem. Some should be fairly straightforward, some will not.