Installation

To install FAST, do the following :

  1. Download FAST and add all the content of the src/ to the Matlab path (right-click on the folder in the Matlab explorer - "Add to path" - "Selected folder and subfolders") ;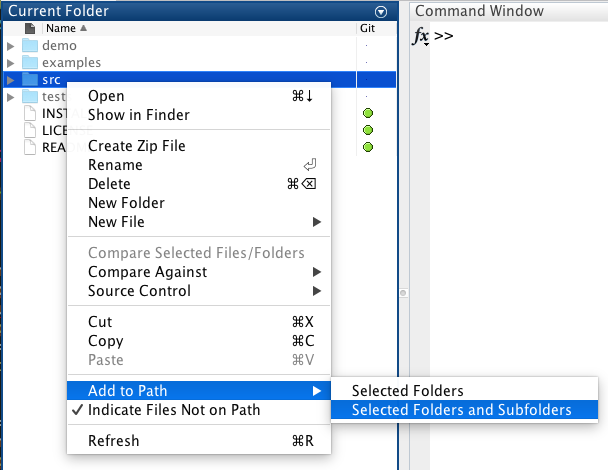 add_path
  2. If you plan to use an external solver, download and install it, and then add it to the Matlab path. If you have and intent to use linprog (which we do not recommend given that it is not that robust), you don't need to do anything.
  3. Run the demo/demo_optimize_stock.m to check that everything is ok. If it outputs two figures, you're good to go. If it does not, make sure the solver selected is the right one.
That's it :-).

For solver installation, you'll have to refer yourself to the solver documentation. Usually, this implies downloading the code, adding it to the Matlab path and setting a few environment variables (that's the annoying part).

A first example : Production Planning

This example can be run interactively using the demo/interactive_demo_optimize_stock.m file (just run this file and follow instructions in the Matlab prompt), or in a more classical way using the demo/demo_optimize_stock.m file.

This problem is the production planning under uncertainty problem. Assume we have a product that we can produce at time 1, and that we can sell at time 2. The main issue is that at time 2, the demand is uncertain.

To fix ideas, assume we produce, at time 1, \(x\) of our product, and that we sell \(s\) of it at time 2. \(C\) will denote the unit cost of production, \(P\) the sale price. \(d(\xi)\) is the (random) demand at time 2. Stated like that, at time 1, the problem is $$ NLDS(1) = \min_{x} C x $$ $$ x \geq 0 $$ while at time 2 we have $$ NLDS(2,\xi) = \min_{s} – P s $$ $$ s \geq 0 $$ $$ s \leq d(\xi) $$ $$ s \leq x $$

This formulation is the most important piece of information. It will be used to describe to the toolbox what problems need to be solved at each node. We can already notice a few key facts: at time 1, we only have variables from time 1 ; at time 2, we have variables from time 2, and the variables (solution) from time 1 can appear in the right-hand side of the constraints, linearly. Same for the random parameter, that can appear linearly in the right-hand side of the constraints.

Now let's turn ourself to the implementation of this problem.

The lattice

The lattice is what will be used to describe the evolution of the uncertainty, the number of scenarios, etc. In this problem, we will assume the random demand (at stage 2) \(d(\xi)\) can take two different values (low or high) with equal probability. At stage 1, we don't have any uncertainty. To represent that, we will use a scenario tree (a lattice), with one node at time 1 and 2 nodes at time 2. Assume we have defined the following demand function 

function out = demand(t,i)
% We don't have any randomnes at stage 1, no we don't store anything
if t == 1 
    out = [] ;
% At time 2, the demand is random, either 2 or 3, depending on the scenario:    
else 
    if i == 1
        out = 2 ;
    elseif i == 2
        out = 3 ;
    end
end
end
The following lines of code 
H = 2 ;
nNodes = 2 ;
lattice = Lattice.latticeEasy(H, nNodes, @demand) ;
build a lattice with \(H = 2\) stages (time-steps), and with 1 node at stage 1 and 2 at stage 2. All transition probabilities are \(1/2\). The third argument of the function latticeEasy is optional, and is used to store some information at each node of the scenario tree. If provided, it should be a function of two arguments, the time t and the index of the node i. It can return anything you want, and the data returned will be stored in the scenario tree, and available when building the NLDS problems.

To help visualise what the lattice is, the function plotLattice is quite useful. In this case, it plots the following (the figure was slightly modified by hand)

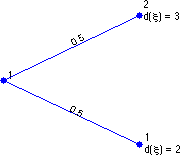
optimize_stock_lattice

The numbers indicate the id of each of the node. We see that at stage 1, there is only one node, with equal probabilities (1/2) to go to each of the nodes of stage 2. At stage 2, there are 2 nodes, where the random demand \(d(\xi)\) is either 2 or 3.

The variables

Now that the scenario tree has been created, we need to define the variables of our problem, namely \(x\) and \(s\). To do so, we simply type something like 

x = sddpVar(1,1) ;
s = sddpVar(1,1) ;
Note that the 1,1 are optional (x = sddpVar() would have been just fine) but used to emphasize the fact that x and y are scalars.

The NLDS

Now, let’s turn to the core of the problem, the definition of the NLDS problems. It will describe what needs to be solved at each stage. The aim of this function is to return the constraints and the objective function at every stage. Note that it is completey different whether scenario.time equals 1 or 2. In the second case, it will differ depending on the value of the demand, stored in scenario.data.

function [cntr, obj] = nlds(scenario, x, s)
C   = 1 ;
S   = 2 ;

% It at stage 1, the problem is
%           min C x + E(V(x))
%           s.t.  x >= 0
% So we write the following constraints :
%           x >= 0
% and the objective function, without the E(V(x)) : the toolbox
% automatically takes care of that
%           min C * x
if(scenario.time == 1)
    % Constraint
    cntr = x >= 0 ;
    % Objective
    obj  = C * x ;
end

% If at stage 2, the problem is
%           min - P s
%           s.t.  s >= 0
%                 s <= d(xi)
%                 s <= x
% (by default we minimize, so the '-' is needed)
if(scenario.time == 2)
    % Constraints
    pos             = s >= 0 ;
    notExceedDemand = s <= scenario.data ; % data is the random demand store into each node (scenario)
    notExceedStock  = s <= x ;
    % Concatenate all constraints together
    cntr = [notExceedDemand ; notExceedStock ; pos];
    % The objective
    obj = -S * s;
end
end

Everything together

We can now put everything together, as shown by the following file. A few last things are needed in order to run SDDP. We first "compile" the lattice with the models 

lattice = lattice.compileLattice(@(scenario)nlds(scenario,x,s)) ;
Note that the variables need to be passed to the nlds function one way or another. But you should not define the variables inside nlds.

We then define a few parameters using the sddpSettings() function. 

params = sddpSettings('algo.McCount',10, ...
                      'stop.iterationMax',10,...
                      'stop.pereiraCoef',0.1,...
                      'solver','linprog')
It is using this function that you can set up all the parameters of the algorithm. Take a look at the help of the function by typing help sddpSettings in the Matlab prompt. Important : you should set up the right value for solver. If you don't have Gurobi (gurobi) or Cplex (cplex), put Linprog (linprog) as a solver. We do recommend using gurobi or cplex if possible.

We finally call the sddp function using the compiled lattice and the parameters using 

output = sddp(lattice,params);
The complete code is thus 
% DEMO OPTIMIZE STOCK
clc ; close all ; clear all ;

%% 1. Lattice creation
H = 2 ;
nNodes = 2 ;
lattice = Lattice.latticeEasy(H, nNodes, @demand) ;
figure ;
lattice.plotLattice(@(data) num2str(data)) ;

%% 2. Variables declaration
x = sddpVar(1,1) ;
s = sddpVar(1,1) ;

%% 3. NDLS declaration
lattice = lattice.compileLattice(@(scenario)nlds(scenario,x,s)) ;    

%% 4. Run SDDP !
params = sddpSettings('algo.McCount',25, ...
                      'stop.iterationMax',10,...
                      'stop.pereiraCoef',2,...
                      'solver','linprog') ; % You need to adapt this for your solver.                  
output = sddp(lattice,params) ;
lattice = output.lattice ;

plotOutput(output) ;

%% 5. Finally, retreive the solution.
nForward = 10 ;
for i = 1:nForward
    [~,~,~,solution] = forwardPass(lattice,'random',params) ;  
    xVal(i) = lattice.getPrimalSolution(x, solution) ;
    sVal(i) = lattice.getPrimalSolution(s, solution) ;
end
disp('x') ;
disp(xVal) ;
disp('s') ;
disp(sVal) ;
Again, notice the following: the function nlds passed to compileLattice should take exactly one argument, a scenario. It is very important that the variables x and s are defined outside of the function. They should be the same between the different calls to nlds so that the program can make the link between the different stages.

The last bit of code is used to retreive the optimal solution. You can ignore it for now. But if you're curious, here's how it works : after completion of sddp, we retreive the lattice and the cuts using lattice = output.lattice. We then do a series of forward pass using the forwardPass function. Then, using the result, we assign to xVal and sVal the numerical value using 

xVal(i) = lattice.getPrimalSolution(x, solution) ;
sVal(i) = lattice.getPrimalSolution(s, solution) ;
We then display the values.

The output of the algorithm, displayed using 

plotOutput(output)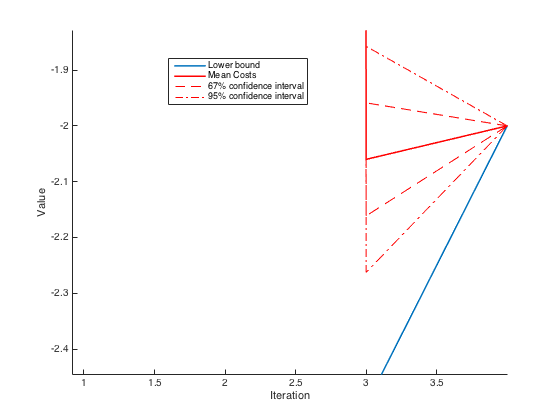
is

demo_conv

We see that at iteration 4, the algorithm has converged, since the lower-bound is equal to the (estimated) mean cost.