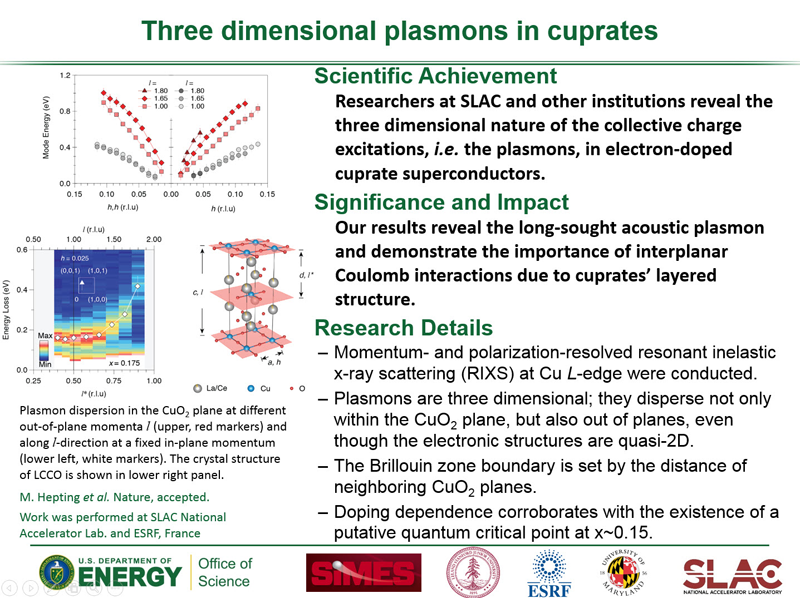
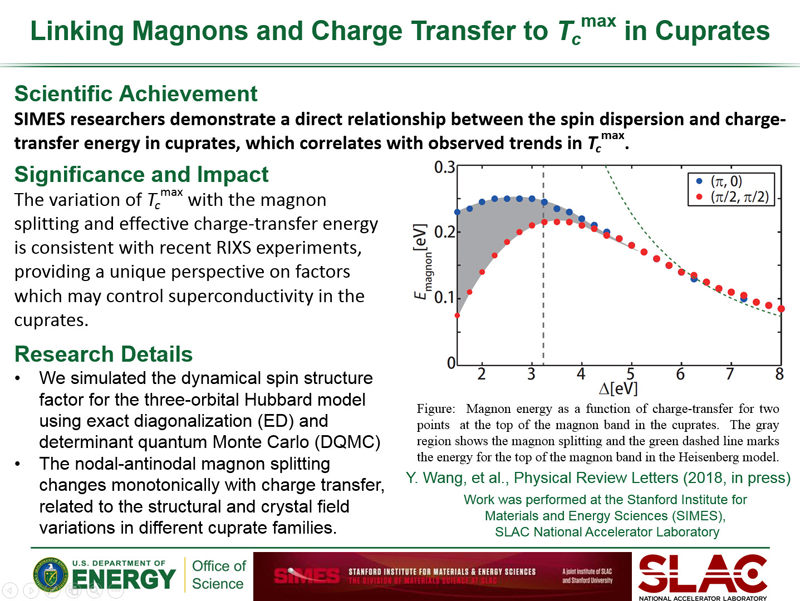
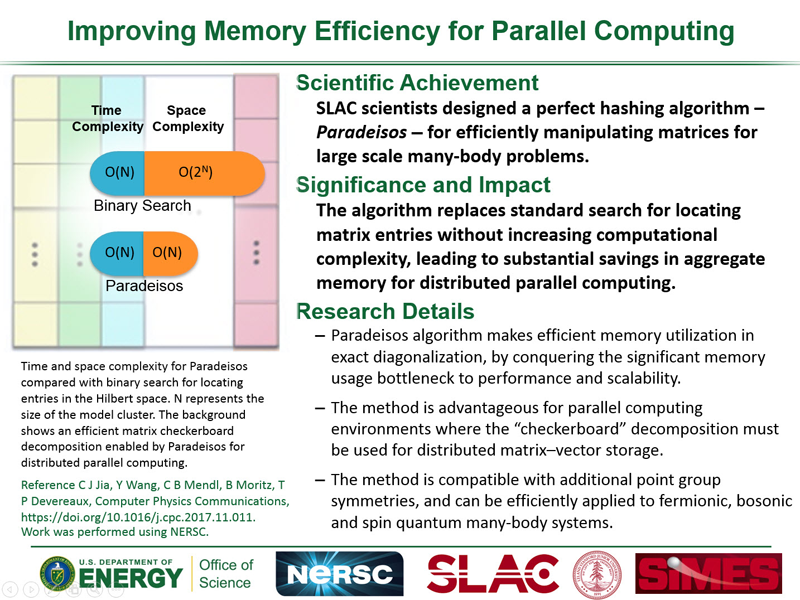
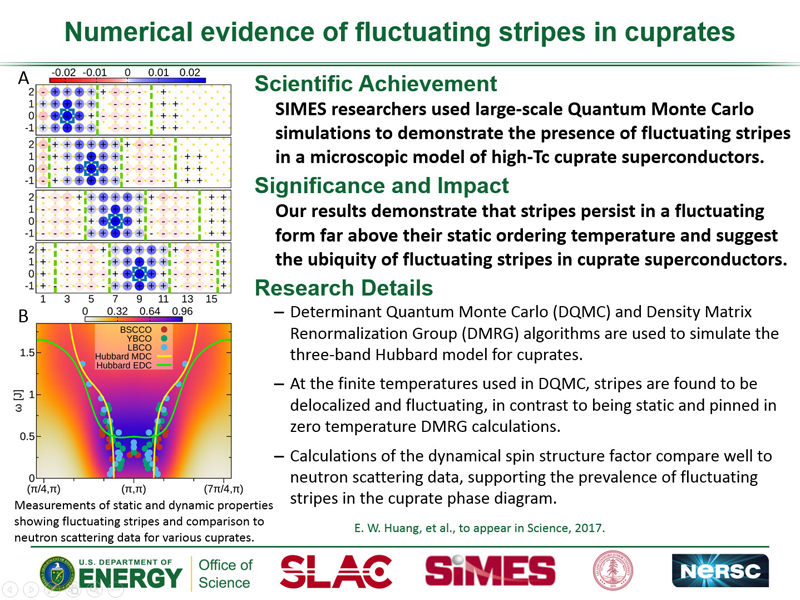
Time Domain Spectroscopy

Cartoon animation of a time-resolved pump-probe photoemission experiment. An initial, low energy (red) laser pulse excites the system followed by a higher energy (blue) laser pulse ejecting electrons detected by an electron analyzer. (Animation courtesy F. Schmitt)
Time-Resolved Photoemission
Photoemission spectroscopy (PES) already provides valuable information about single-particle electron dynamics in condensed matter systems and the technique recently has been extended to the time-domain (tr-PES) using pump-probe, femto-second techniques, providing new information on electron dynamics. One of the first successes involved collectively driving a system between two states of matter (charge density wave (CDW) state and normal state) and identifying characteristic frequencies in the temporal evolution of the spectral intensity. One of the first handful of experiments was conducted by our experimental collaborators, appearing in Science. In the experiment, signatures of the CDW amplitude mode, a collective mode of the underlying charge modulation, were revealed directly in the temporal dynamics of the PES response. These experiments have provided detailed information about the coupling between electrons and the underlying lattice; and, other advances have extended the technique into the atto-second regime which opens the possibility of observing and controlling dynamics on time-scales relevant to correlated electron processes.
"Hot" Electrons, Quasi-equilibrium, and Electron Correlations
Most pump-probe experiments have been interpreted in terms of "hot" electrons, equilibrated at highly elevated, effective temperatures. This approach captures a redistribution of spectral intensity, but does not account properly for the rearrangement of accessible electronic states nor does it properly capture the nonequilibrium redistribution of spectral weight between these states that accompanies pump-pulses with the high excitation densities needed to drive phase transitions or excite electronic collective modes.
To directly address these issues in a controlled fashion, we have examined the time-domain response of a correlated electron system driven toward a nonequilibrium steady state by an intense DC field. We employed dynamical mean-field theory (DMFT) to study the nonequilibrium Keldysh boundary problem for the spinless Falicov-Kimball model at half-filling. Effects due to the finite temporal width of the photoemission probe-pulse with adjustable time delay were introduced by partially transforming the nonequilibrium double-time lesser Greens function to real frequency. The formalism was developed by our collaborators in a recent article.
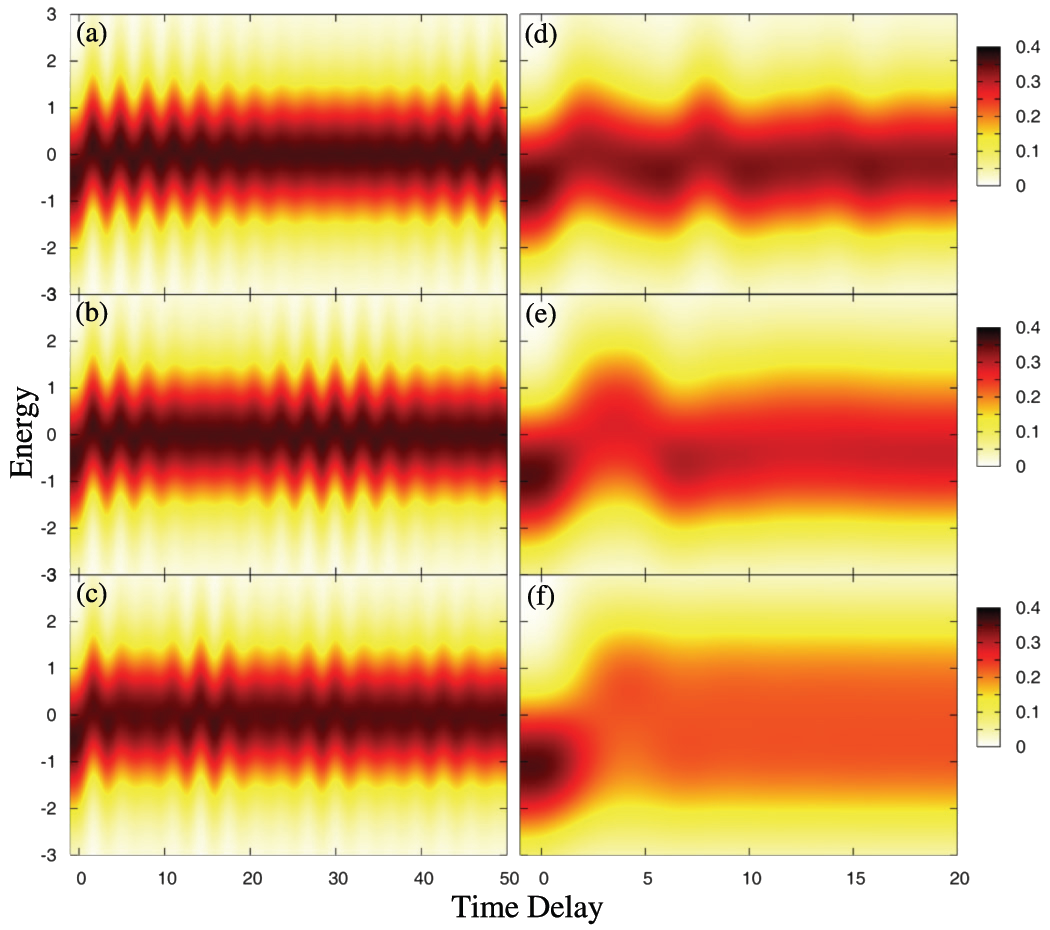
Panel of figures highlighting the tr-PES response for a given probe-pulse shape as a function of the Falicov-Kimball model interaction strength, (a)-(f). The final two panels, (e) and (f), show the response for a system on the insulating side of the Mott metal-insulator transition (MIT). Note the appearance of Bloch oscillations for weak interactions and an additional low frequency modulation proportional to the interaction strength. The systems approach a nonequilibrium steady state, but this is only apparent for fairly wide probe-pulses that effectively average the response over a wide temporal range. Taken from Reference 4.
Our initial studies were made possible by an INCITE award at NERSC for studying the time-domain response of the spinless Falicov-Kimball model subject to a time-dependent electric field. The codes were extensions of the massively parallel code used to study the same hamiltonian with DC driving fields. This work made use of the previous generation of supercomputers at NERSC: the Cray XT4 system Franklin and the Cray XE6 system Hopper.
These results help to gauge the relaxation of a pumped system back toward equilibrium by observing the evolution of the equal-time distribution function. The panels below show the distribution function, starting in equilibrium, through the application of the pump-pulse, and during relaxation. Each test case represents a different set of simulation parameters with the first representing a system on the metallic side of the MIT and the second representing an insulating system. Note that while the system attempts to return to an equilibrium-like distribution (at a higher effective temperature) in the metallic regime (Case 1), in the insulating regime, the system retains a nonequilibrium distribution of electrons even at long times following the pump-pulse (Case 2). These distribution functions are plotted in "band energy" space rather than momentum space as described in this reference work.
Case 1: Evolution of the momentum distribution for a metallic system (U=0.5) pumped by a Gaussian waveform with an additional harmonic modulation (ω=0.5). Pump #2 refers to a sequence of different pump pulses simulated for these experiments. Adapted from material in Reference 5.
Case 2: Evolution of the momentum distribution for an insulating system (U=2.0) pumped by a harmonically modulated Gaussian waveform as in the case above (ω=0.5). Pump #2 refers to a sequence of different pump pulses simulated for these experiments. Adapted from material in Reference 5.
Electron-Phonon Coupling and Relaxation
The influence of other degrees of freedom (primarily the lattice or phonons) on the relaxation dynamics in pump-excited electron systems can be explored using a very similar Keldysh approach, where the influence of the lattice degree of freedom is included via a simple Migdal approximation for the self-energy and one evaluates the contribution to the electron self-energy using the lowest order electron-phonon diagram in the Born limit. We have shown that the dynamics of the phonon mediated recovery occurring at long times is controlled by the equilibrium self-energy as a function of momentum and frequency in the normal state.
In this sequence we see the evolution of the change in the electron distribution in the first Brillouin zone and the subsequent recovery through the electron-lattice interaction. Notice the "fringes" associated with oscillations of the distribution whose frequency is related to the underlying phonon frequency. Adapted from material in Reference 6.
Panel of figures highlighting the tr-ARPES response for a given probe-pulse shape within the Migdal approximation for the electron-phonon interaction. Particular emphasis is placed on the apparent recovery of the system at long times and the fact that significant redistribution of spectral weight remains in the ARPES response within the window of the phonon frequency. The last two panels highlight the deviation between the measured response at long times at two different temperatures and that measured in equilibrium. These results are quite reminiscent of those appearing in Nature Physics on the time evolution of a pump excited cuprate superconductor from the experiments conducted by the Lanzara group. Taken from Reference 6.
Amplitude Mode, or "Higgs" Oscillations, in a Superconductor
We also examined the time-dependent dynamics in the superconducting state for the electron-phonon coupled model which exhibits s-wave pairing in equilibrium. Applying a pump pulse in the superconducting state can suppress, but not entirely eliminate superconductivity, depending on the strength of the applied field (vector potential A(t)). In the Nambu formalism, this can be seen in the change of the anomalous density, reflecting the change in the strength of the superconducting order, as a function of time. The spectra, as well as the anomalous density, exhibit oscillations as shown in the panels of the following figure. These oscillations occur at a frequency ω=2Δ(∞) reflecting the Anderson-Higgs amplitude mode of the superconductor, arising in a full Migdal-Eliashberg treatment of the problem.

Snapshots of the spectral function illustrating the oscillations as a function of time. The times are chosen to show the spectrum before the pump (a) and at the minima/maxima of the amplitude mode oscillations (b-e). Panel (f) shows the anomalous density, demonstrating suppressing, but not complete melting, of the superconducting state, as well as the applied vector potential. Taken from Reference 7.

Oscillations in the EDC maximum as a function of time showing the changes in the "Higgs" frequency with the strength in the applied field. As the field strength decreases to zero, the suppression of the superconducting state and the amplitude of the oscillations decreases, but the frequency extrapolates to that one would derive from the equilibrium magnitude of the superconducting gap as shown in the inset. Taken from Reference 7.
Time-Resolved X-ray Scattering
Tme-resolved soft X-ray scattering from condensed matter systems at the LCLS and ALS combines experimental and theoretical studies of THz or infrared laser pulses which drive a system out-of-equilibrium and an X-ray pulse, either from the free-electron laser (FEL) source or synchrotron, which probes the system. Theoretically, we attack this problem using the machinery developed for studying the X-ray scattering cross-section in equilibrium, primarily exact diagonalization and Krylov time-evolution, together with phenomenology. Below is a schematic of the theoretical approach for one particular type of X-ray scattering problem looking at the time dependence of orbital excitations: solve the equilibrium problem to determine the ground state and final states, evaluate the time-evolution operator (or an approximation) acting on the appropriate states to determine their time-dependence, and evaluate the cross-section as a function of pump-probe delay. Initial experiments performed at the SXR beamline of the LCLS were highlighted in an article in Nature Communications, which details the recovery of a stripe-ordered nickelate system following optical pump excitation.
Schematic of the algorithm used to determine the tr-IXS cross-section. This schematic shows the steps for an L-edge IXS process where a core-hole/valence-electron pair (a hole in the Core Levels and an extra (red) electron in the Valence Levels) exists in the intermediate state. (Figure courtesy W.-S. Lee)
Ultrafast pulses which drive a system out of equilibrium can tip the balance between intertwined degrees of freedom and in the process modify the phase and electronic structure of a material. It can often be difficult to disentangle this information as a function of frequency, or as a function of time, if these degrees of freedom, predominantly lattice phonon modes, have similar time/energy scales and influence a material system simultaneously with a strength that may depend subtly on the complicated path a material takes to its out-of-equilibrium state. This can be true in iron-based superconductors where a strong coupling exists between electrons and the lattice, inducing closely tuned structural and magnetically ordered ground states with different fluctuations serving to provide a playground for ultrafast manipulation. In photoexcited BaFe2As2 one particular mode dominates above the others and a change in the internal structure of the unit cell can be derived from X-ray scattering measurements of the change in the Bragg peaks. While the underlying crystal symmetry remains unchanged during ultrafast optical pumping, a single A1g mode, known to modulate the Fe–As–Fe bond angle, is launched with a modification of the pnictogen position, or height above the Fe plane. This change in pnictogen position induces significant changes in the electronic structure, which in-turn drive changes in the underlying tendencies of model systems to order magnetically. This type of ultrafast structural manipulation can be important for designing methods to manipulate electronic properties and tip the balance between phases in quantum materials.

(a) Crystal structure of BaFe2As2 showing the elongation of the pnictogen position following ultrafast pumping. The impact of the A1g phonon is captured by the change in the Fe–As–Fe bond angle α. (b) An experimental schematic in which incoming infrared (IR) pump (red) and X-ray probe (blue) can be used to determine the time-dependent changes in the Bragg peaks and infer the time-dependent changes in the pnictogen bond angle. Taken from Reference 9.

(a) DFT can be used to assess the effect of a change in the pnictogen height (Fe-As-Fe bond angle) on the band structure in BaFe2As2. The equilibrium bands (solid lines) shift as a result of the change in the Fe–As–Fe bond angle (dashed lines). Bands have been coded with dominant dxz (red), dyz (green), and dxy (blue) character. (b,c) Sections near zone center and zone corner showing the change in effective band overlap near the Fermi energy due to the change in bond angle induced by the pump. These show improved nesting of bands with similar orbital character (dxy) at zone corner. (d) Self-consistent Hartree–Fock mean-field calculations for the relative change of the SDW ordering temperature. The arrow indicates a 6.5% increase in TN for the experimentally observed change in the Fe–As–Fe bond angle. Taken from Reference 9.
Taking advantage of the ability to derive atomic motion from time-resolved X-ray scattering data, especially when the atomic motion remains relatively simply, offers a unique opportunity. As the electronic structure can be modified significantly due to the motion of individual atoms or the collective oscillations associated with driving specific phonon modes, combining time-resolved X-ray scattering to extract structural information with tr-ARPES to assess the impact on the electronic bands themselves can provide direct experimental access to the deformation potential, the central ingredient in assessing the strength of electron-phonon coupling. Again, the iron-based superconductors provide a unique playground. FeSe displays oscillations from a single phonon mode associated with the c-axis oscillation of the Se atoms following ultrafast infrared pumping. At the same time, it has been suggested that electron-electron interactions in FeSe, which appear to be the largest in any iron-based superconductor, can enhance significantly the electron-phonon coupling. However, a unique, experimental verification of this assumption has proven quite elusive. By combining these two time-domain experiments into a “coherent lock-in” measurement in the terahertz regime, where X-ray diffraction tracks coherent lattice motion and photoemission monitors the subsequent coherent changes in the electronic band structure, the deformation potential can be determined for this compound due to the single phonon mode. Comparison with DFT-derived estimates for the deformation potential shows an enhancement of the coupling strength in FeSe, likely due to effects from strong electronic correlations. Electron-phonon coupling's importance in superconductivity may imply that this enhancement points to a cooperative interplay between electron-electron and electron-phonon interactions in the iron-based superconductors.

(A) Plots showing derived changes in chalcogenide height and measured changes in the band positions in FeSe following ultrafast excitation using two complementary techniques: tr-XRD and tr-ARPES. (B) Schematic of the A1g phonon mode (top), which periodically modulates the electronic band energies (bottom). (C and D) Amplitudes of the oscillations as a function of the incident pump fluence. Solid lines indicate linear fits and the shading represents systematic fluence uncertainties. Taken together, these measurements constitute an ultrafast coherent "lock-in" experiment to determine the deformation potential due to this phonon mode. Taken from Reference 10.
Nonequilibrium Steady-States and Floquet Theory
Manipulating materials properties far from equilibrium has been exemplified by the transient melting and/or enhancement of electronic orders in charge-density-wave, magnetic, and superconducting systems. That out-of-equilibrium driving can affect electronic transport holds an equally significant promise for manipulating conduction channels and electronic switching. The conceptually simplest way of treating these effects is through Floquet-Bloch, steady-state theory where temporally broad pump pulses dress the bands with multiple copies separated by of the underlying carrier frequency of the pulse. This description has been validated for the surface states of a topological insulator, where circularly polarized light breaks time-reversal symmetry, dynamically lifting the Dirac point degeneracies, and where the Floquet-Bloch side-bands can be clearly distinguished in the response. An extension of these phenomena to proper topological phase transitions remains well beyond experimental reach in most materials due to large electric fields required to open a sizeable gap or the possibility of resonant absorption and sample heating.
These issues may be partially overcome in monolayer transition-metal dichalcogenides, novel materials which constitute a realization of massive relativistic Dirac fermions in two dimensions: graphene with a gap. The bandstructure, and sizeable gap to charge excitations, allows a new picture to develop in these materials. The added complexity of a realistic materials description leads to a new mechanism to optically induce topologically protected chiral edge modes, facilitating optically switchable conduction channels that are insensitive to disorder. Where as massive graphene and other toy models treat only the two massive Dirac cones, TMDCs possess an intrinsic three-band nature in monolayers. The subsequent photo-induced band inversions scale linearly in applied pump field and exhibit transitions from one to two chiral edge modes on sweeping from red to blue detuning. Our ab initio, non-equilibrium Floquet–Bloch theory has been illustrated for WS2, but the general results are not particularly sensitive to microscopic materials details.

Calculations showing the band dispersion for a ribbon of TMDC material driven into a nonequilibrium steady-state. (a) In equilibrium, the ribbon hosts two trivial edge states localized at opposing edges (thin red lines inside the gap). (b) A red-detuned pump field induces a hybridization gap at the bottom of the conduction band, which scales linearly in A until closing again at a critical pump strength. This gap hosts one non-trivial edge state. (c) A blue-detuned pump couples the equilibrium valence and conduction bands, inducing gaps both at the bottom of the conduction and top of the valence band. These host two chiral edge conducting channels. (d) Hybridization gaps at the opposite valley K' lead to a trivial band inversion, depicted here for the top of the valence band for blue detuning. Taken from Reference 11.
While the search for quantum spin liquids involves various candidate materials, an experimental confirmation of a gapped topological spin liquid remains elusive. In much the same way that light may be used to manipulate the electronic bandstructure, it may also be used to manipulate a system at the Hamiltonian level, thereby inducing a true topological phase transition. Using circularly polarized light, one can effectively tune materials parameters, under the correct circumstances, to drive a frustrated Mott insulator toward a chiral spin liquid. Again, using Floquet theory to derive a proper spin model, the dynamics of a driven Kagome Mott insulator involve an induced scalar spin chirality term Si·(Sj×Sk), which dynamically breaks time-reversal while preserving SU(2) spin symmetry. This dynamical symmetry breaking may hold the key to engineering elusive quantum phases that are not readily accessible in equilibrium.

(a) A driven Kagome Mott antiferromagnet, pumped with circularly polarized light, dynamically breaks time-reversal and parity while preserving SU(2) spin symmetry, inducing scalar spin chirality terms Si·(Sj×Sk) in the Hamiltonian. (a) Evolution of spin (circles on vertices) and chiral (triangles) correlation functions with pump strength A. (b) Minimum chiral spin liquid (CSL) excitation gap serving as a gauge of the phase as a function of pump frequency and strength. The inset depicts the twofold quasi-degenerate ground state (blue and dashed-red lines) and gap to excited states (brown lines) for flux insertion. The equilibrium ground state (a putative Z2 spin liquid or valence bond crystal VBC) transitions into a photo-induced CSL at finite pump strength. Adapted from Reference 12.
References and External Links
- A. P. Jauho and J. W. Wilkins, Phys. Rev. B 29, 1919-1938 (1984).
- J. K. Freericks, Phys. Rev. B 77, 075109 (2008).
- J. K. Freericks, H. R. Krishnamurthy, and Th. Pruschke, Phys. Rev. Lett. 102, 136401 (2009).
- B. Moritz, T. P. Devereaux, and J. K. Freericks, Phys. Rev. B 81, 165112 (2010).
- B. Moritz et al, Phys. Rev. Lett. 111 077401 (2013).
- M. Sentef et al, Phys. Rev. X 3, 041033 (2013).
- A. F. Kemper et al, Phys. Rev. B 92, 224517 (2015).
- W.-S. Lee et al, Nature Comm. 3 838 (2012).
- S. Gerber et al, Nature Comm. 6, 7377 (2015).
- S. Gerber et al, Science 357, 71-75 (2017).
- M. Claassen et al, Nature Comm. 7, 13074 (2016).
- M. Claassen et al, Nature Comm. 8, 1192 (2017).
Shen Laboratory: Time-resolved Spectroscopy
Ultrafast Surface Dynamics: Research Group of Prof. Martin Wolf
Uwe Bovensiepen Research Group
Lanzara Research Group
Max Planck Research Department: Structural Dynamics: Andrea Cavalleri




























































Connect with Me