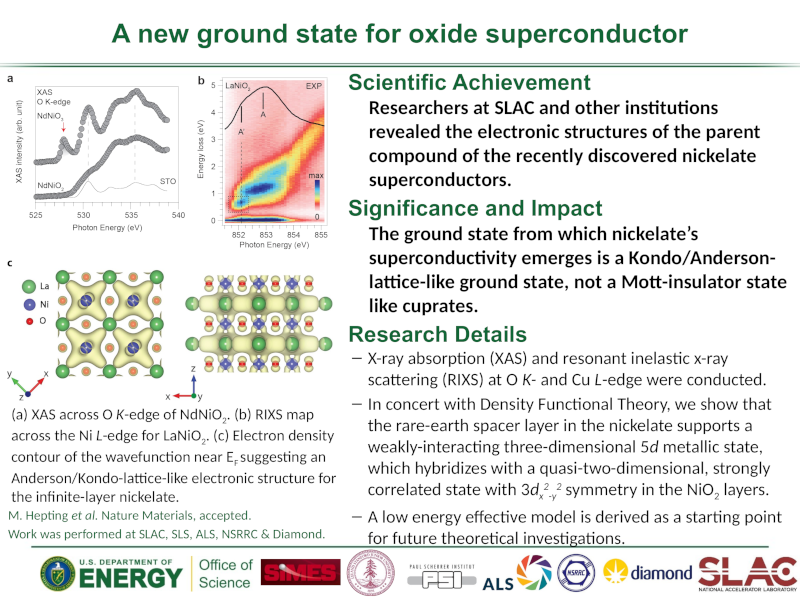
X-ray Scattering

Resonant inelastic X-ray Scattering (RIXS) is one of the most important experimental probes for studying strongly correlated materials. RIXS is a photon-in/photon-out process, and by observing the frequency shift and polarization change of the outgoing photon compared to the incoming photon, properties of the material's electronic structure can be measured. A schematic representation of the RIXS scattering process is shown below:

RIXS has the ability to highlight momentum-dependent many-body excitations essential for understanding the material properties of strongly-correlated systems. This second-order RIXS process may be described in two steps such that starting from the ground state an optical excitation accesses the intermediate state where a localized core-hole is created and photoelectron gets promoted to a higher energy band. The de-excitation from the intermediate state to final state proceeds via the emission of a scattered photon, leaving the system in an excited state with energy and momentum transferred from the incident photon. While ARPES reveals the momentum resolved single-particle spectral function of occupied states, the momentum-depednent RIXS process involves both occupied and unoccupied states such that one readily obtains information regarding the electron or charge transfer dynamics involving multi-particle excitations.

Many exciting RIXS measurements have already been reported, and it is generally believed that RIXS can be a new powerful tool to probe the interplay between charge, spin, orbital, and lattice degrees of freedom. However, these experimental results are not fully understood. Previous theoretical RIXS studies include methods based on some approximations such as finite-order perturbation theory or Hartree-Fock approximations, where correlation effects are poorly treated, or methods based on small cluster configuration interaction or numerical Lanczos techniques in which the Hilbert space is truncated and the intermediate state profiles are in general not captured as accurately as one might desire. One way we have proceeded has been to tackle this problem using numerical exact diagonalization for a multi-orbital Hubbard model on small clusters, form which one has direct accesses to the eigenvalues and eigenvectors of the initial, intermediate, and final states without truncation. In combination with information from the valence and conduction band density of states provided by DFT, the momentum-dependent RIXS spectra can be constructed, and their resonance profiles can be characterized and compared to experiment (see the references).

The low x-ray emission efficiency problem for x-ray beamlines has been improved with the advances in high brilliance undulator light sources as well as the use of highly efficient detectors. RIXS energy resolution has reached to better than 100 meV, and further improvements can be expected in the near future. At the same time, development in theory is crucial to provide understanding toward the new physics revealed from these RIXS measurements.

L-edge RIXS: A Measure of the Spin Response

Doping quantum antiferromagnets presents a number of intriguing possibilities given the complicated phase diagrams which typically emerge from strongly correlated, Mott materials upon chemical substitution. A primary question in these materials is the nature of the coherent quasiparticles that emerge and form the low energy degrees of freedom. Recent RIXS experiments in hole-doped cuprates purported to measure collective spin excitations that persist well into the overdoped regime and bear a striking resemblance to those found in the parent compound. The ability of RIXS to measure spin excitations in the soft x-ray region stems from the strong spin-orbit coupling which exists in the core levels accessed in an L-edge experiment. However, these experimental results challenge our usual notions that spin excitations should weaken with doping, and in principle, have a diminishing effect on superconductivity.

Using small cluster exact diagonalization, we have shown in a series of works that RIXS indeed is sensitive to the spin structure factor at the transition metal L-edges. Further, using determinant quantum Monte Carlo calculations for the single-band Hubbard model, we have evaluated the doping dependence of the spin excitation spectrum upon changing the electron count away from the parent antiferromagnetic insulator. At relatively high temperatures, we have been able to demonstrate that the portion of the spectrum to which RIXS is sensitive in momentum space remains relatively unchanged in terms of energy scale with hole doping; and in fact, our results show that the excitations should harden with electron doping. The latter result has been confirmed by additional experiments on electron doped Nd_2-xCe_xCuO₄ (NCCO) compounds. This non-intuitive behavior can be understood by analyzing the effective low energy, spin-like theory that emerges from a perturbation expansion. Additional hole-delocalization terms act as an effective spin exchange, which mitigates the softening of the spin excitations upon hole doping and leads to a hardening of those same excitations with electron doping.

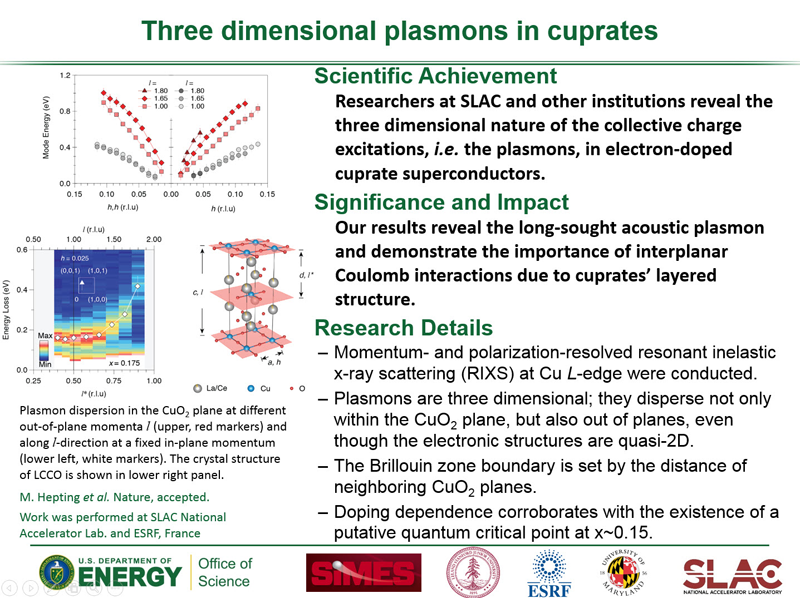
RIXS for Collective Charge Excitations and Phonons

With sufficient energy resolution, RIXS can be an ideal probe for revealing a variety of excitations arising from orbital, spin, charge, and lattice degrees of freedom. Information about these elementary excitations in energy and momentum space can be deduced from analyzing the RIXS spectra as functions of the energy loss and the momentum transfer of the photons. As discussed above, RIXS recently has played a pivotal role in revealing the evolution of magnetic excitations in cuprates. In addition, RIXS provided the first X-ray scattering evidence for an incommensurate charge density wave (CDW) in this same class of compounds. The shape of the quasi-elastic signal in these systems hints at other low energy excitations that may manifest in the RIXS response. In a recent work, we have shown that RIXS can be an ideal probe for studying the bosonic momentum dependence of the electron-phonon coupling (Reference 8), which should manifest in the RIXS response at these low energies.

Using ultrahigh-resolution RIXS, not only can one observe the CDW in underdoped Bi_2.2Sr_1.8Ca_0.8Dy_0.2Cu₂O_8+δ, but at low temperatures, one can observe the dispersive collective acoustic excitations from the CDW. These excitations enhance the density of states in the vicinity of the phonon and induce an anomalous enhancement in the RIXS intensity. This behavior can be adequately captured in a phenomenological model for the interplay between the phonon degrees of freedom and the enhanced density of states due to the soft charge mode near the CDW wavevector. The dispersive CDW excitations, phonon anomaly, and analysis of the CDW wavevector provide a comprehensive momentum-space picture of complex CDW behaviour and a possible close tie to the pseudogap state.

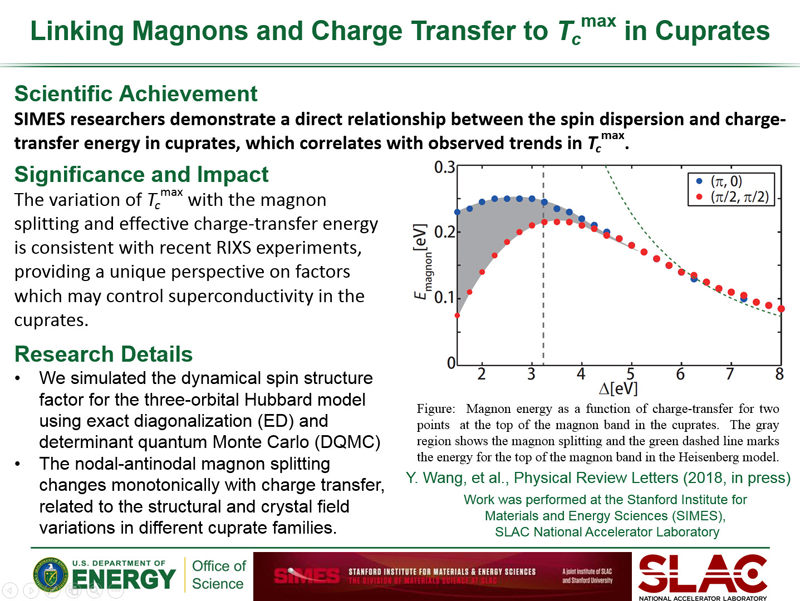
Stripes

Doped Mott insulators exhibit symmetry breaking in the form of charge and spin density waves organized into patterns known as stripes. In the cuprates, at incommensurate filling, these stripes have been suspected to exist in a fluctuating form. Resonant x-ray scattering can provide valuable information on the incommensurate Bragg peaks observed for static stripe formation. Neutron scattering experiments, which are complementary to RIXS measurements and provide a direct measure of the spin response function, can provided considerable experimental insight into the phenomena of spin stripes. The "hourglass" spectrum near the AFM wavevector at (π,π) has been viewed as evidence for fluctuating stripes in the cuprates. To observe and characterize stripes in microscopic models for these systems would provide an important theoretical lens for understanding the rich cuprate physics.

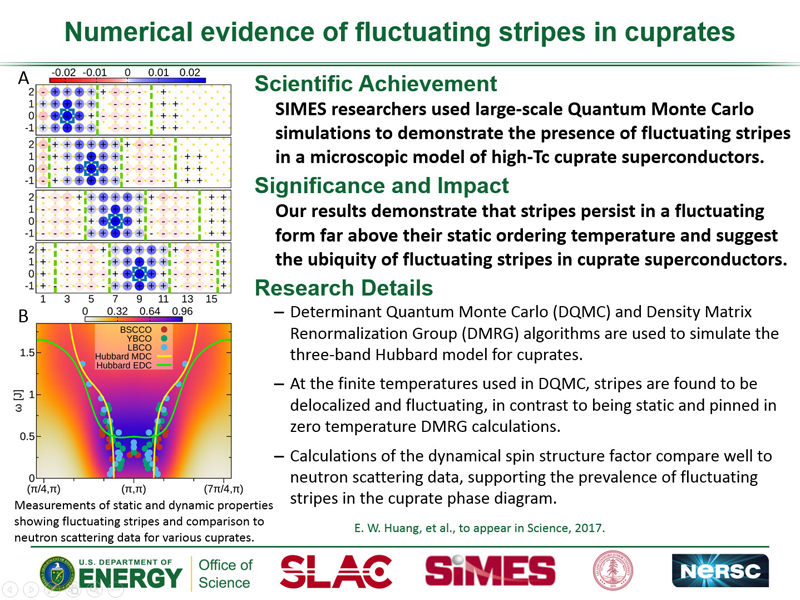
Previous mean-field studies of the Hubbard model demonstrate a propensity for doped holes to aggregate into lines of charge. These boundaries form antiphase domain walls for spin stripes. These findings have been substantiated with more sophisticated treatments that demonstrate the presence of charge and spin stripes in the ground state of the Hubbard model. Using numerically exact determinant quantum Monte Carlo (DQMC) simulations, we find evidence for dynamical, fluctuating spin stripes at high temperatures in the Hubbard model. These fluctuating spin stripes display an antiphase AFM pattern; however, the charge stripes that form the antiphase domain walls are not pinned in the underlying lattice, essentially making them free to move and leading to fluctuating spin stripe behavior. This stands in stark contrast to the behavior found in zero temperature DMRG calculations, where the charge and spin stripes remain pinned by the boundaries of the small cluster used in the simulations.

We also calculated the dynamical spin structure factor S(Q,ω) to compare with neutron scattering experiments and other x-ray scattering experiments that can provide access to the spin response function. In the parent compound the structure factor shows a clear peak in the intensity and dispersion minimum at (π, π), as expected for an antiferromagnet. With hole doping, the high-energy portions of the spectrum are relatively unaffected, as we know from RIXS measurements in these compounds. The soft excitations near the AFM wavevector lose spectral weight and harden, giving rise to an increase in the singlet-triplet gap and the destruction of AFM ordering. At wave vectors with incommensurability corresponding to the real-space periodicity of the spin stripes, a qualitatively distinct behavior emerges where the excitations tend to soften with doping. This behavior peaks in the vicinity 1/8^th doping before giving way to a uniform hardening and loss of spectral weight at higher hole dopings.

This nonmonotonic behavior motivates a comparison to the universal hourglass spectrum seen in inelastic neutron scattering. If one plots the center positions of momentum distribution curve (MDC) fits to the calculated structure factor for hole doping with experimental data from different compounds, there is a remarkable agreement. For low energies, the MDC fits do not resolve the neck of the hourglass, given the high temperature and limited momentum resolution of the DQMC simulation. Taking energy distribution curve (EDC) fits, one correctly resolves the collection of spectral intensity around the position of the hourglass. With this in mind, the low-energy incommensurability agrees reasonably well with the experimental results. Furthermore, the doping dependence of the incommensurability follows a trend similar to the points of the experimental Yamada plot. The correspondence with well-established experimental results implies that the Hubbard model simulation may be capable of capturing the microscopic features necessary to understand essential collective properties and the fluctuating stripe physics of the cuprates.

---

References and Suggested Reading

1. Akio Kotani and Shik Shin, Rev. Mod. Phys. 73, 203 (2001).
2. L. J. P. Ament et al, Rev. Mod. Phys. 83, 705 - 767 (2011).
3. F. Vernay et al, Phys. Rev. B 77, 104519 (2008).
4. C.-C. Chen et al, Phys. Rev. Lett. 105, 177401 (2010).
5. C.J. Jia et al, New J. Phys. 14, 113038 (2012).
6. C.J. Jia et al, Nature Comm. 5, 3314 (2014).
7. W.-S. Lee et al, Nature Phys. 10, 883-889 (2014).
8. T. P. Devereaux et al, Phys. Rev. X 6, 041019 (2016).
9. L. Chaix et al, Nature Phys. 13, 952-956 (2017).
10. E. W. Huang et al, Science 358, 1161-1164 (2017).

ID32, ESRF
The ADRESS Beamline, SLS
Beamline 41A, TPS
Milano Group
Abbamonte Group, UIUC
Young-June Kim Group, Toronto