Exam Statistics
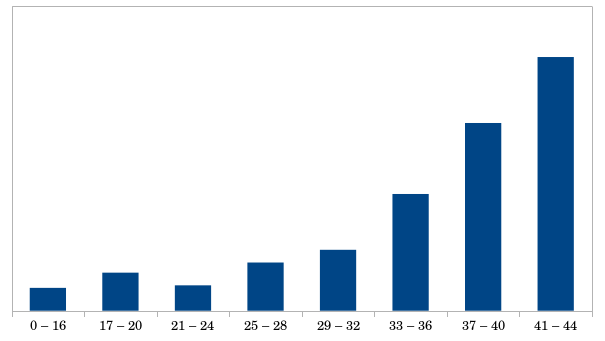
Here's a histogram of the scores on this exam:
To contextualize this, here are the quintile scores:
- 80th Percentile: 42 / 44 (95%)
- 60th Percentile: 40 / 44 (91%)
- 40th Percentile: 36 / 44 (82%)
- 20th Percentile: 29 / 44 (66%)
Exam scores, along with the graders' feedback, are available online on Gradescope.
If you have any questions about the exam, please feel free to reach out to us. Keith and Neel will be holding their normal office hours this week, and the section leaders will be setting up dedicated time slots to meet with those of you who want to go over the exam. We'll make an announcement about this later this week.
Problem One: Exit Light (8 Points)
Lights Out is a puzzle game. You are given a grid of buttons. Each button is either lit up or is dark. We’ll represent the grid of buttons as a Grid<bool>, where truemeans “the button is lit” and false means “the button is dark.”
If you push a button, it changes which buttons are lit. Specifically, the button itself and the up to four buttons adjacent to it in the four cardinal directions (up, down, left, right) will all toggle; each of those buttons will become lit if it is dark and will become dark if it is lit.
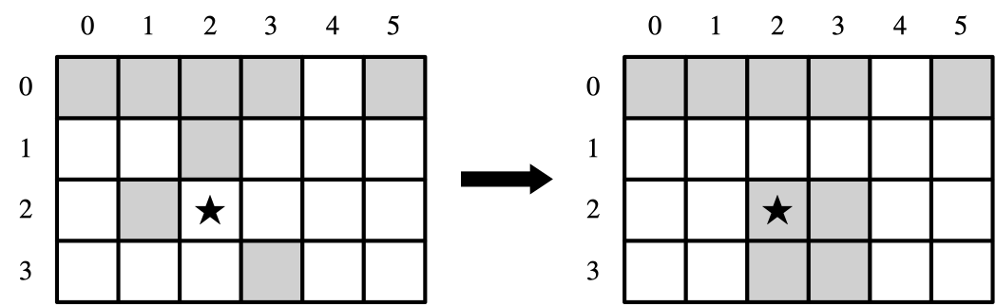
For example, here’s a sample Lights Out grid and the effect of pressing the button at row 2, column 2:
As the name Lights Out suggests, the goal of the puzzle is to turn out all the lights. Write a function
bool solvesPuzzle(Grid<bool>& lights, const Vector<GridLocation>& presses);
that takes as input a Grid<bool> and a list of buttons that were pressed in the order in which they were pressed. Your function should then modify the lightsparameter to simulate the effect of pushing all those buttons in that order. Your function should then return true if after pushing all those buttons the lights are all turned off and return false otherwise. If any of the button presses are at positions off the grid, you should call error to report an error.
As a refresher, here’s the definition of the GridLocation type:
struct GridLocation {
int row;
int col;
};
/* Flips the light at a given position. */
void flip(Grid<bool>& lights, int row, int col) {
if (lights.inBounds(row, col)) {
lights[row][col] = !lights[row][col];
}
}
/* Returns if all the lights are off. */
bool isDark(const Grid<bool>& lights) {
for (int row = 0; row < lights.numRows(); row++) {
for (int col = 0; col < lights.numCols(); col++) {
/* Light on? Then they're not all off. */
if (lights[row][col]) return false;
}
}
return true;
}
bool solvesPuzzle(Grid<bool>& lights,
const Vector<GridLocation>& presses) {
/* Press all the buttons. */
for (GridLocation loc: presses) {
/* Validate input. */
if (!lights.inBounds(loc)) {
error("You're really pushing my buttons!");
}
/* Flip the five lights. */
flip(lights, loc.row, loc.col);
flip(lights, loc.row + 1, loc.col);
flip(lights, loc.row - 1, loc.col);
flip(lights, loc.row, loc.col + 1);
flip(lights, loc.row, loc.col - 1);
}
return isDark(lights);
}
Why we asked this question: This question was designed to let you show off what you'd learned in the two grid-based assignments from the start of the quarter (Fire from Assignment 1; Rising Tides from Assignment 2). The neighbor-processing code was designed to call back to Assignment 2's propagation of water to neighboring locations, and the bounds-checking and looping over all locations was meant as a callback to Assignment 1.
Common mistakes: The most common mistake on this problem was correctly validating that a button was in bounds, but not checking whether its neighbors were in bounds before toggling them from on to off or vice-versa. That's an easy mistake to make and fortunately it's very easy to correct as well! Similarly, some solutions only toggled a button's neighbors, not the button itself, or otherwise didn't toggle the correct buttons. At the very end, we saw some solutions that stopped as soon as they found a single light turned off, rather than checking to see if all the lights were off. And there were a few submissions here and there that had trouble identifying the neighboring locations of a cell.
Problem Two: Vexillology (8 Points)
Many countries have the same color schemes for their flags. For example, the flags of the United States, Slovenia, Costa Rica, Nepal, Liberia, New Zealand, and Samoa (among others) use red, white, and blue. The flags of Senegal, Grenada, and Lithuania (among others) use red, green, and yellow.
You will be given a Map<string, Set<string>> structured as follows. Each key will be a color name (e.g. "white", "gold", "black"). Each value is a Set<string>containing the names of all countries that have that color on their flag. For example, the key "white" would be associated with the set { "United States", "India", "Argentina", "Indonesia" ... }, and the key "red" would be associated with the set { "United States", "China", "Cameroon", ... }.
Your job is to produce a Map<Set<string>, Set<string>> whose keys are sets of colors and whose values are names of countries that use exactly those colors on their flags. For example, the set of colors { "red", "white", "blue" } would be a key whose associated value would be the set of countries { "United States", "Slovenia", "Costa Rica", ... } because those countries’ flags use the colors red, white, and blue and no others. The key { "red", "white" } would be associated with the set { "Indonesia", "Latvia", "Peru", ... }, but that set of countries would not contain the country "United States" because the US flag uses blue in addition to red and white.
Write a function
Map<Set<string>, Set<string>>
countriesByColors(const Map<string, Set<string>>& colors);
that converts the initial map (keys are colors, values are sets of countries that have that color on their flags) into the final map (keys are sets of colors, values are sets of countries that use exactly those colors on their flags).
Some notes on this problem:
- Although this problem involves sets and subsets, this is not meant to be a recursion exercise and we aren’t expecting you to write recursive code to generate subsets.
- As a hint, we recommend creating an intermediary
Mapthat associates each country with the set of all colors that appear on its flag. - Countries may use any number of colors on their flags, not just two or three. Therefore, each country may be an element of any number of the value
Sets in the initial input map. - Each country should be an element of exactly one of the value
Sets in the resulting map.
Map<Set<string>, Set<string>>
countriesByColors(const Map<string, Set<string>>& colors) {
/* Map from countries to their set of colors. */
Map<string, Set<string>> countries;
for (string color: colors) {
/* Each of the countries here has this color on its flag. */
for (string country: colors[color]) {
countries[country] += color; // Autoinsert
}
}
/* Invert that map to get the result. */
Map<Set<string>, Set<string>> result;
for (string country: countries) {
/* The set of colors associated with this country becomes the
* key. The country itself gets added to the value set. As
* before, we use autoinsertion to make this compact.
*/
result[countries[country]] += country;
}
return result;
}
Why we asked this question: This question was designed to let you show what you'd learned about the Map and Set types, as well as your familiarity looping over unordered containers. We picked this specific problem because it focused heavily on the distinction between keys and values in sets; you don't need to write that much code here, but the code you write needs to have a high attention to detail to ensure you don't mix up countries and colors. Finally, we included this problem because it's a fantastic place to show off the Map's autoinsertion feature. That's not necessary to solve this problem, but it definitely makes things easier!
Common mistakes: This was the highest-scoring problem on the exam by average score - nicely done, folks! The most common mistakes we saw were mixing up +, =, and += when inserting items into the value Sets within a Map. Some solutions also had trouble looping over the nested sets in the original colors map, mostly due to mixing up keys and values.
Many solutions didn't rely on autoinsertion, which is not wrong per se but introduces a few more opportunities for mixups. We saw some type errors where folks tried assigning strings to Set<string>s or vice-versa, which won't work correctly. But these sorts of errors are easily fixed.
Problem Three: The Solomon Islands (8 points)
In this problem, we have provided you code for two recursive functions along with inputs to those func- tions. Trace through the recursive functions on those inputs and tell us what those functions return. No justification is necessary.
i. (4 Points) Consider the following function:
string auki(const string& kirakira) {
if (kirakira.length() <= 1) {
return "NORO";
}
return kirakira[1] + auki(kirakira.substr(2)) + kirakira[0];
}
What does auki("TULAGI") return?
Here's one way to see this function in action:
auki("TULAGI")returns'U' + auki("LAGI") + 'T'.auki("LAGI")returns'A' + auki("GI") + 'L'.auki("GI")returns'I' + auki("") + 'G'.auki("")returns"NORO".
- … so
auki("GI")returns"INOROG".
- … so
auki("LAGI")returns"AINOROGL".
- … so
auki("TULAGI")returns"UAINOROGLT".
Thus the overall answer is "UAINOROGLT".
Why we asked this question: We included this question to see if you were comfortable mechanically tracing through a recursive string-processing function along the lines of what you saw in our lecture in Week 1, in the Only Connect exercise from Assignment 1, and in the Protein Synthesis problem from Assignment 3. The twist we included here is that we grow the string from both ends in this problem, which requires some attention to detail as you rearrange the characters and results in an interesting phenomenon: the even-indexed characters appear at the back of the string in reverse order, and the odd-indexed characters appear at the front of the string in the same relative order that they occur in the original string.
Common mistakes: Many solutions correctly worked out that the string would start with "UAI" and end with "GLT", but forgot to include the "NORO" in the middle from the base case. Some solutions also misplaced the "NORO" at the end of the string.
We also saw a number of solutions that claimed that the call to kirakira.substr(2) would crash when kirakira had length 2. This turns out not to be the case. To see why this is, consider a length-two string, like this:
+---+---+
| H | I |
+---+---+
0 1 2
Here, I've marked the separators at the boundaries of characters. If this string is kirakira, then kirakira.substr(1) would grab everything at or after separator 1 ("I"), and kirakira.substr(2) would grab everything at or after separator 2 ("").
ii. (4 points) Consider the following function:
string honiara(int n) {
if (n <= 1) {
return to_string(n); // Converts n to a string; e.g. 1 becomes "1".
} else {
string isatabu = to_string(n);
honiara(n - 1);
isatabu += 'X';
isatabu += honiara(n - 2);
return isatabu;
}
}
What does honiara(4) return?
Tracing through this one requires keeping track of a few important details.
- Each call to
honiaragets its own independent copy ofisatabu, which is completely separate from each other call's version. - The
returnstatement in the base case does not end the entire chain of recursive calls. - Because the result of the call to
honiara(n - 1)is not stored anywhere, that recursive call has no effect on the version ofisatabuin the calling function.
With this in mind, here's what happens.
honiara(4)setsisatabu = "4"and callshoniara(3). The return value of that call is not used, so we can skip evaluating it. We then appendXtoisatabuto getisatabu = "4X", then append whateverhoniara(2)returns toisatabu.honiara(2)setsisatabu = "2"and callshoniara(1). The return value of that call is not used, so we can skip evaluating it. We then appendXtoisatabuto getisatabu = "2X", then append whateverhoniara(0)returns toisatabu.honiara(0)returns"0".
- … so we append
"0"toisatabuto getisatabu = "2X0", which we then return.
- … so we append
"2X0"toisatabuto getisatabu = "4X2X0", which we then return.
So the overall answer is "4X2X0"
Why we asked this question: This question was designed to hit at the three key aspects of recursion outlined above. Each of these is a common sticking point as folks learn recursion, and wanted to give you a chance to show what you'd learned in those areas.
Common mistakes: Most of the mistakes we saw on this problem resulted from errors in interpreting the three points above. For example, we saw many solutions of "1", which results from assuming that the first return statement reached ends the full recursive call chain, and a few copies of "4X2X1", which results from starting off correctly but then interpreting the first base case reached as the last value appended. We also saw many copies of "2X0", which happens if you assume there's just one isatabu that is repeatedly overwritten. Finally, we saw many solutions that incorporated the results of the discarded honiara(n - 1) call.
Problem Four: Fold and Press (8 points)
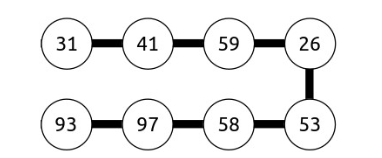
You are given a strand of ints, like the one shown here:
Imagine folding this strand of ints so that the back half of the numbers are aligned perfectly under the front half, like this:
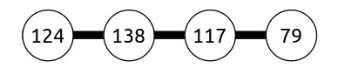
Now, imaging “pressing” the top half into the bottom half by adding each number in the top half with the number underneath it in the bottom half, yielding this smaller strand:
We’re now left with a strand that’s half as long as before. Write a recursive function
Vector<int> foldAndPress(const Vector<int>& strand);
that takes in a Vector, then folds and presses it along the lines of what’s described above. For example,
calling foldAndPress({ 31, 41, 59, 26, 53, 58, 97, 93 }) returns { 124, 138, 117, 79 }. If the input Vector has odd length, then it cannot be folded and pressed, and you should call error to report an error.
Some notes on this problem:
- Your solution must be purely recursive. You may not use loops of any sort (
for,while,do…while, orgoto). - You might find the
Vector’ssubListfunction helpful; it works just like thestring’ssubstrfunction. - Look for a pattern in how the numbers in the input
Vectorare paired off.
This solution is based on the following recursive observation:
- If the strand is empty, then folding and pressing it into itself yields an empty strand.
- Otherwise, the first and last numbers in the strand are folded and pressed together, and the rest of the sequence then consists of a folded-and-pressed version of the remaining numbers.
Here are two variations on this solution strategy:
/* Solution Route 1: No helper, build up Vector through recursive calls. */
Vector<int> foldAndPress(const Vector<int>& strand) {
if (strand.size() % 2 != 0) {
error("Parity disparity - verily!");
} else if (strand.isEmpty()) {
return { };
} else {
int length = strand.size();
return (strand[0] + strand[length - 1]) +
foldAndPress(strand.subList(1, length - 2));
}
}
/* Solution Route 2: Same idea as above, but use a soFar parameter to track
* what's been folded and pressed thus far.
*/
Vector<int> foldAndPressRec(const Vector<int>& strand,
const Vector<int>& soFar) {
if (strand.size() % 2 != 0) {
error("Bummer - need another number.");
} else if (strand.isEmpty()) {
return soFar;
} else {
int length = strand.size();
return foldAndPressRec(strand.subList(1, length - 2),
soFar + strand[0] + strand[length - 1]);
}
}
Vector<int> foldAndPress(const Vector<int>& strand) {
return foldAndPressRec(strand, { });
}
There's another way to do this. You can cut the strand in half to form two smaller strands. Then, you recursively repeatedly match the first number from the first half with the last number in the second half.
/* Solution Route 3: Take from the front and the back. */
Vector<int> foldAndPressRec(const Vector<int>& front,
const Vector<int>& back) {
if (front.size() == 0) {
return { };
} else {
int sum = front[0] + back[back.size() - 1];
return sum + foldAndPressRec(front.subList(1),
back.subList(0, back.size() - 1));
}
}
Vector<int> foldAndPress(const Vector<int>& strand) {
if (strand.size() % 2 != 0) {
error("Even this number is too odd...");
} else {
int half = strand.size() / 2;
return foldAndPressRec(strand.subList(0, half),
strand.subList(half));
}
}
Why we asked this question: We included this problem because we thought it was a great example of a pure recursion problem that doesn't involve backtracking, enumeration, or all those other patterns. Cracking this problem requires a series of simple insights: which items get added together, what elements are left over, and how those items get placed relative to the others.
Common mistakes: We saw a number of solutions that chose a vector of length two as a base case rather than a vector of length zero. This will work for all strands except for a strand with no numbers. That is an unusual case to consider, but it's one that is important to think about. As you've seen over the course of the quarter, thinking about the absolute simplest possible inputs is an important skill when training yourself to think recursively.
Many solutions had the right idea of pairing off two numbers and recursively processing the rest, but did so by pairing off the wrong numbers - typically, the first number and the number right after the middle.
Some solutions forgot to capture the return value from the foldAndPress recursive call after making it. Remember - if you make a recursive call that returns a value, it's important to do something with that value to prevent it from getting discarded.
And finally, we saw a number of scattered errors involving invalid Vector syntax, small off-by-one or indexing errors into Vectors, etc. But those are, fortunately, pretty easy to fix.
Problem Five: In-N-Out (12 points)
Consider the following setup. We are given a Queue<int> holding some values. We are also given an empty stack. We then repeatedly choose one of the following two operations until the queue and stack are both empty:
- Dequeue from the queue and push the dequeued number onto the stack.
- Pop from the stack and write down that number.
At the end of this process, we’ll have written down a sequence of numbers. If the queue originally holds the sequence 1, 2, 3, in that order, there are five possible such sequences:
- Push 1, Pop 1, Push 2, Pop 2, Push 3, Pop 3: The result is
{ 1, 2, 3 }. - Push 1. Pop 1. Push 2. Push 3. Pop 3. Pop 2. The result is
{ 1, 3, 2 }. - Push 1. Push 2. Pop 2. Pop 1. Push 3. Pop 3. The result is
{ 2, 1, 3 }. - Push 1. Push 2, Pop 2. Push 3. Pop 3. Pop 1. The result is
{ 2, 3, 1 }. - Push 1. Push 2. Push 3. Pop 3. Pop 2. Pop 1. The result is
{ 3, 2, 1 }.
On the other hand, if the original Queue<int> held the sequence 1, 2, 3, 4, then there are 15 sequences we could form:
- Push 1. Pop 1. Push 2. Pop 2. Push 3. Pop 3. Push 4. Pop 4. The result is
{ 1, 2, 3, 4 }. - Push 1. Pop 1. Push 2. Pop 2. Push 3. Push 4. Pop 4. Pop 3. The result is
{ 1, 2, 4, 3 }. - Push 1. Pop 1. Push 2. Push 3. Pop 3. Pop 2. Push 4. Pop 4. The result is
{ 1, 3, 2, 4 }. - …
- Push 1. Push 2. Push 3. Push 4. Pop 4. Pop 3. Pop 2. Pop 1. The result is
{ 4, 3, 2, 1 }.
Write a function
Set<Vector<int>> stackSequencesFor(Queue<int> queue);
that takes as input a Queue<int>, then returns a Set containing all possible orderings of the elements of that Queue that can arise by starting with an empty Stack and performing a series of operations given by the rules above (either dequeue from the queue and push onto the stack, or pop from the stack).
We recommend that you make this function a wrapper around a recursive function
Set<Vector<int>> stackSequencesRec(Queue<int> queue,
Stack<int> stack,
const Vector<int>& soFar);
Some notes on this problem:
- Your solution must use recursion.
- Think about the decision tree. At each point in time, you have (up to) two options: dequeue from the queue and push to the stack, or pop from the stack. Use recursion to explore each of these options and gather together all the possible sequences that can result from doing so.
Here are two slightly different ways of solving this problem, each of which is a variation on something we encountered in the course of grading the exam.
/*************************** Version 1 ****************************/
/* Given the stack and queue, and the sequence we've built thus far, return a set of all
* sequences we can make by extending what we have so far.
*/
Set<Vector<int>> stackSequencesRec(Queue<int> queue,
Stack<int> stack,
const Vector<int>& soFar) {
/* Base Case: If the stack and queue are empty, then the only option is
* to keep what we have.
*/
if (queue.isEmpty() && stack.isEmpty()) {
return { soFar };
}
Set<Vector<int>> result;
/* If the queue isn't empty, try shifting into the stack. */
if (!queue.isEmpty()) {
/* Make local copies of the queue and stack so that when we move an
* item from the queue to the stack, we don't modify the
* queue/stack that's seen in the other if statement.
*/
auto nextQ = queue;
auto nextS = stack;
nextS.push(nextQ.dequeue());
result += stackSequencesRec(nextQ, nextS, soFar);
}
/* If the stack isn't empty, pop and append to the output. */
if (!stack.isEmpty()) {
int next = stack.pop();
result += stackSequencesRec(queue, stack, soFar + next);
}
return result;
}
Set<Vector<int>> stackSequencesFor(Queue<int> queue) {
return stackSequencesRec(queue, { }, { });
}
/*************************** Version 2 ****************************/
/* Given the stack and queue, and the sequence we've built thus far, return a set of all
* sequences we can make by extending what we have so far.
*/
Set<Vector<int>> stackSequencesRec(Queue<int> queue,
Stack<int> stack,
const Vector<int>& soFar) {
/* Base Case: If the queue is empty, transfer everything out of the
* stack.
*/
if (queue.isEmpty()) {
auto result = soFar;
while (!stack.isEmpty()) {
result += stack.pop();
}
/* This is the only option. */
return { result };
}
Set<Vector<int>> result;
/* If the stack isn't empty, pop and append to the output. */
if (!stack.isEmpty()) {
int next = stack.pop();
result += stackSequencesRec(queue, stack, soFar + next);
/* Reset the stack. &/
stack.push(next);
}
/* We know the queue isn't empty. Shift into the stack. */
stack.push(queue.dequeue());
return result + stackSequencesRec(queue, stack, soFar);
}
Set<Vector<int>> stackSequencesFor(Queue<int> queue) {
return stackSequencesRec(queue, { }, { });
}
Why we asked this question: This problem was designed to let you show off what you've learned about recursive enumeration over the course of the past few weeks. We picked this specific problem both because it covers stacks and queues (which didn't get any airtime elsewhere on the exam) and because the decision tree has a slightly different shape than what we've seen thus far - it's neither a "loop over all options" nor an "include/exclude" pattern. We also liked how it involved maintaining a collection of data structures across the recursion and keeping track of how those data structures change from one recursive call to the next.
Common mistakes: This was the trickiest problem on the exam largely because there are a number of important details to keep in mind as you're working through it.
One of the most common mistakes on this problem was to modify the Stack or Queue when making one of the recursive calls in a way that interfered with the other recursive call. For example, suppose you dequeue from the Queue and push onto the Stack for the first recursive call. Then as you start considering the second call, you have to be mindful that the queue no longer has its original elements and that the stack has one too many elements. The two solutions shown above handle this in different ways.
Another common class of mistakes involved syntax errors with the stack and queue in the context of making recursive calls. Remember that the function calls stack.pop() and queue.dequeue() remove and return an item from the container. You therefore cannot pass stack.pop() as a parameter into a function expecting a Stack<int>, because stack.pop() returns an int. Similarly, the stack.push() and queue.enqueue() functions return void rather than producing a new Stack or Queue. Thus you can't pass stack.push(queue.dequeue()) into a function expecting a Stack<int>.
Coming up with the right base case for this problem is also a bit tricky. As shown above, there are two reasonable base cases to consider. The first is when both the stack and queue are empty (you're done, and soFar is the only sequence you can make), and the second is when the queue is empty (you have to empty the stack out). We saw some solutions that stopped entirely as soon as the queue was empty without emptying the stack, which will cause an incomplete soFar to appear in the output. We also saw many solutions that returned soFar rather than { soFar }, which is on the right track but doesn't work because the types are wrong.
Finally, we saw a number of mistakes that arose from incorrectly aggregating the recursive call results together. Some solutions returned too early, only making a single recursive call total. Others made recursive calls but forgot to store the results.