Mazes

A maze is a twisty and convoluted arrangement of corridors that challenge the solver to find a path from the entry to the exit. This assignment is about using ADTs to represent, process, and solve mazes.

An introduction to mazes

Labyrinths and mazes have fascinated humans since ancient times (remember Theseus and the Minotaur?), but mazes can be more than just recreation. The mathematician Leonhard Euler was one of the first to analyze plane mazes mathematically, and in doing so, he founded the branch of mathematics known as topology. Many algorithms that operate on mazes are closely related to graph theory and have applications that include diverse tasks such as designing circuit boards, routing network traffic, motion planning, and social networking.

In this part of the assignment, you'll be writing function to verify and generate maze solution paths. We will focus on a particular type of maze known as a perfect maze. A perfect, or simply-connected, maze has no loops and no inaccessible areas. Any two locations within a perfect maze are connected by exactly one path.

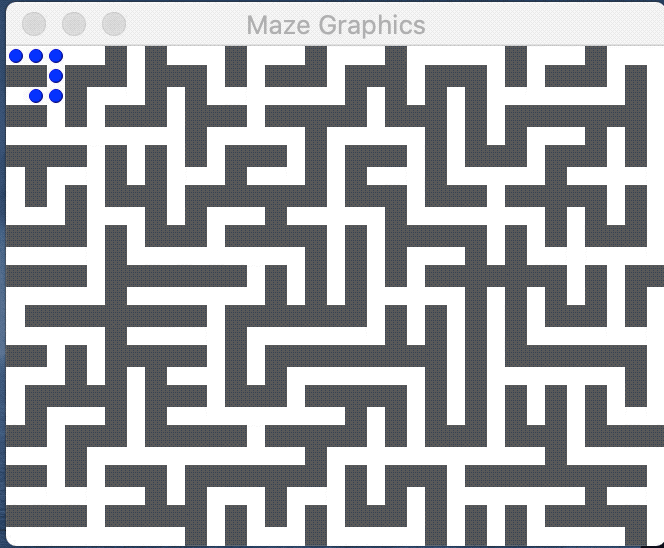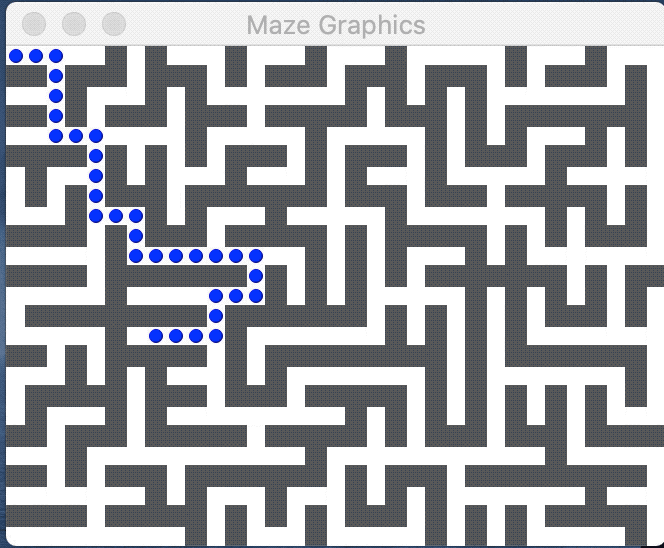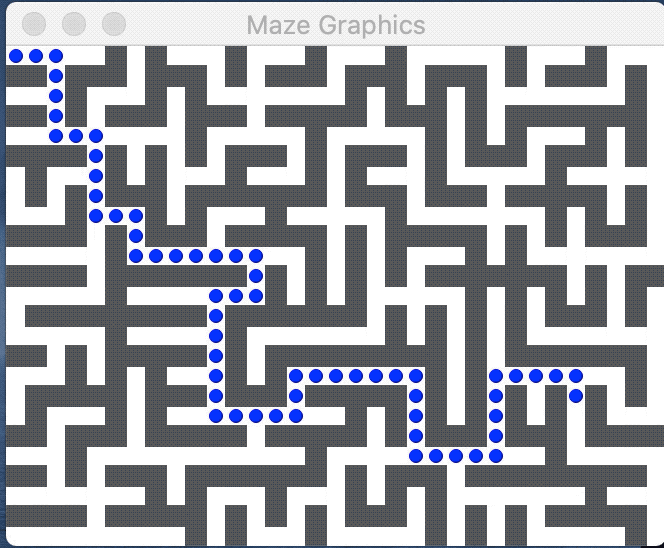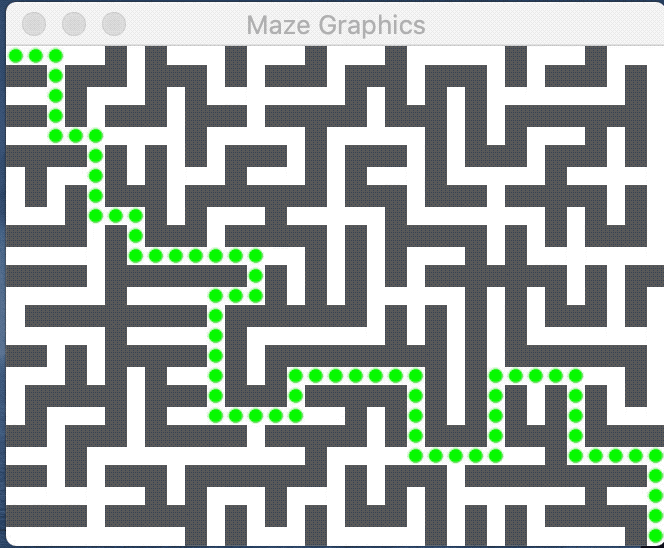
The image below shows a perfect maze and the path from the entry at upper left to exit at lower right:

This introduction section explains how we will represent mazes, the ADTs we will use, and the structure of the maze data files we have provided. Please carefully read this section before you jump into coding.

A Grid represents a maze

A maze can be modeled as a two-dimensional array where each element is either a wall or a corridor. The Grid class from the Stanford library is a good tool for representing a maze.

• A maze is represented as a Grid<bool>. We use a value of true to represent an open corridor and false for a wall.
• Accessing grid[row][col] will evaluate to true if there is a open corridor at location row,col and false if it is a wall.

A maze is read from a text file. Each line of the file corresponds to one row of the maze. Within a row, the character @ is used for walls and - for corridors. Here is a sample 5x7 maze file:

-------
-@@@@@-
-----@-
-@@@-@-
-@---@-

Our starter code provides the readMazeFile function that reads a text file in the above format into a Grid<bool>. In the project "Other files/res" folder are a number of provided maze files. If you wish to create your own maze file, you can right-click and duplicate an existing maze file inside Qt Creator.

A GridLocation is a row/col pair

While working with the maze grids, you will find it handy to use the GridLocation struct. A GridLocation has two fields, row and col, that are packaged together into one aggregate type. The sample code below demonstrates using a GridLocation variable and assigning and accessing its row and col fields.

 // Declare a new GridLocation
 GridLocation chosen; // default initialized to 0,0
 chosen.row = 3;      // assign row of chosen
 chosen.col = 4;      // assign col of chosen
 
 // Initialize row,col of exit as part of its declaration
 GridLocation exit = { maze.numRows()-1, maze.numCols()-1 }; // last row, last col 

 // You can use a GridLocation to index into a Grid (maze is a Grid)
 if (maze[chosen]) // chosen was set to {3, 4} so this accesses maze[3][4]
 ...

 // You can directly compare two GridLocations
 if (chosen == exit)
 ...

 // You can also access a GridLocation's row,col separately
 if (chosen.row == 0 && chosen.col == 0) 
 ...

A Stack of GridLocation is a path

A sequence of connecting GridLocations represents a path through the maze. You will use a Stack<GridLocation> to store a path. To extend the path, you simply push an additional GridLocation onto the stack. Peeking at the top of the stack accesses the end of the path. A solution path for the maze starts at the maze entrance (bottom of stack), travels through connecting GridLocations, and ends at the maze exit (top of stack).

Alongside the maze text files in the "Other files/res" folder, there are .soln text files that contain maze solutions. For example, this is the solution file corresponding to the 5x7 maze shown previously. (Note that the entries in a stack are displayed in order from bottom to top)

{r0c0, r0c1, r0c2, r0c3, r0c4, r0c5, r0c6, r1c6, r2c6, r3c6, r4c6}

Our starter code provides the readSolutionFile function that reads a text file in the format above into a Stack<GridLocation>. Not every maze will have a corresponding .soln file, and part of your job will be writing code to generate solutions!

ADT resources

• Lectures: Grid/GridLocation, Stack/Queue
• Documentation for Stanford collections: Grid, GridLocation, Stack, Queue
• Section 6.1 of the textbook introduces struct types
• In the lower-left corner of your Qt Creator window, there is a magnifying glass by a search field. If you type the name of a header file such as grid.h or gridlocation.h , Qt will display the corresponding header file

Notes on Stanford collection types

• The assignment operator works as expected for all our ADTs. Assigning from one Stack/Vector/Set/etc to another will create a copy of the ADT with a copy of the elements.
• Be on your toes about making sure that your template types are always properly specialized and that all types match. Using Vector without specifying the element type just won't fly, and a Vector<int> is not the same thing as a Vector<double>. The error messages you receive when you have mismatches can be cryptic and hard to interpret. Bring your template woes to the Ed forum, and we can help untangle them with you.

Onto the code!

Your work is structured in three tasks: two functions that verify the correctness of a solution path and a final pièce de résistance to generate a solution path. You will also be writing comprehensive test cases for your functions. All of the functions and tests for mazes are to be implemented in the file maze.cpp.

1) Write generateValidMoves()

For your first task, you'll implement the following helper function:

Set<GridLocation> generateValidMoves(Grid<bool>& maze, GridLocation cur)

Given a maze represented as a Grid of bool and a current cell represented by the GridLocation cur, this function returns all valid moves from cur as a Set. Valid moves are defined as follows:

• Either directly north, south, east, or west (N, S, E, W) of cur
• Only one "step" away from cur in the grid
• Is open corridor, not a wall
• Not out-of-bounds of the provided maze

There are a few provided tests for generateValidMoves, but these tests are not fully comprehensive. You should write at least 3-4 additional tests to make sure your helper function works. Remember to label your tests as STUDENT_TEST.

2) Implement checkSolution() to verify a path

Next you'll write a function to confirm that a solution is valid for a particular maze:

void checkSolution(Grid<bool>& maze, Stack<GridLocation> path)

The path represents a valid solution through maze if it meets the following criteria:

• The path must start at the entry (upper left corner) of the maze
• The path must end at the exit (lower right corner) of the maze
• Each location in the path is a valid move away from the previous location
  • call the helper function you already wrote to help confirm a move is valid, rather than re-implement its logic!
• The path contains no loops, i.e. a location appears at most once in the path

If checkSolution detects any of the above problems, it should call the error function from error.h to report an error. This function is used to report a fatal error. When you call error, it halts the program right there and reports the message you passed as an argument:

error("Here is my message about what has gone wrong");

If all of the criteria for a valid solution are met, then checkSolution completes normally.

This function has a lot of things to check and will need rigorous tests to confirm all of its functionality. We've provided some initial tests to get you started, but you will need to write tests of your own. You should write at least 3-4 additional tests of the checkSolution function.

After writing checkSolution you will not only be familiar with using the ADTs to represent mazes, but you will also have a function that makes testing the next milestone much easier. Having thoroughly testing your checkSolution on a variety of invalid paths means you can be confident that it is the oracle of truth when it comes to validating a solution. Your future self will thank you.

Note the use of the special kinds of test cases EXPECT_ERROR and EXPECT_NO_ERROR in our provided tests. An EXPECT_ERROR test case evaluates an expression, expecting that the operation will raise an error. While the test is executing, SimpleTest framework will catch the error, record that it happened, and resume. Because the error was expected, the test case is considered to be passed. If an error was expected but didn't materialize, the test case fails. This is the opposite of an EXPECT_NO_ERROR test case, which does not expect errors and treats a raised error as a test failure. More information on the different test macros and how they all work can be found in the CS106B Testing Guide.

3) Find solutions with solveMaze()

Now you're reading to tackling finding an escape route from a maze. You are to implement the following function, which uses breadth-first search (BFS) to find a valid solution path through a given maze:

Stack<GridLocation> solveMaze(Grid<bool>& maze)

There are a wide variety of algorithms for solving a maze. Solving a maze can be seen as a specific instance of a shortest path problem, where the challenge is to find the shortest route from the entrance to the exit. Shortest path problems come up in a variety of situations such as packet routing, robot motion planning, analyzing gene mutations, spell correction, and more. In the case of the perfect maze, the shortest path is also the only path, but the general process is the same regardless.

Breadth-first search (BFS) is a classic and elegant algorithm for finding a shortest path. A breadth-first search reaches outward from the entry location in a radial fashion until it finds the exit. The first paths examined take one hop from the entry. If any of these reach the exit location, you’re done. If not, the search expands to those paths that are two hops long. At each subsequent step, the search expands radially, examining all paths of length three, then of length four, etc., stopping at the first path that reaches the exit.

Breadth-first search is typically implemented using a queue. The queue stores partial paths that represent possibilities to explore. The paths are processed in order of increasing length. The first paths enqueued are all length one, followed by the length two paths, and so on. Given the FIFO handling of the queue, all shorter paths are dequeued before the longer paths make their way to the front of queue, ready for their turn to be processed.

At each step, the algorithm considers the current path at the front of the queue. If the current path ends at the exit, it is a complete solution. If not, the algorithm takes the current path and extends it to reach locations that are one hop further away in the maze, and enqueue those extended paths to be examined later.

Since a path is represented as a Stack of GridLocations, putting these paths into a queue for processing means you'll have a nested ADT, a Queue<Stack<GridLocation>>. A nested container type looks a little scary at first, but it is just the right tool for this job.

Here are steps followed by a breadth-first search:

1. Create a queue of paths. A path is a stack of grid locations.
2. Create a length-one path containing just the entry location. Enqueue that path.
   • In our mazes, the entry is always the upper-left corner and exit in the lower-right.
3. While there are still more paths to explore:
   • Dequeue path from queue.
   • If this path ends at exit, this path is the solution!
   • If path does not end at exit:
     • For each viable neighbor from path end, make copy of path, extend by adding neighbor and enqueue it.
     • A viable neighbor is a location that is a valid move and that has not yet been visited.

A couple of notes to keep in mind as you're implementing BFS:

• You may make the following assumptions:
  • The maze is well-formed. It is non-empty, fully connected, and entrance at upper-left and exit at lower-right are both open corridors.
  • The maze has a solution.
• You should avoid repeatedly revisiting the same location in the maze or creating a path with a cycle, lest the search get stuck in a infinite loop. For example, if the current path leads from location r0c0 to r1c0, you should not extend the path by moving back to location r0c0.
• You shouldn't use checkSolution within your solveMaze implementation, but you should use it to write tests that confirm the validity of paths found by solveMaze.
• A strategy that will help with both visualizing and debugging solveMaze it to add calls to our provided graphics functions, explained below.

We have provided some existing tests that put your solveMaze functions to the test. You should take advantage of the extra maze files we've provided you and add 2-3 more tests that verify the correct functionality of the solveMaze function.

Add graphics functions to draw the maze

The Stanford C++ library has extensive functionality for drawing and interacting with the user, but we generally don't ask you to dig into those features. Instead, we will supply any needed graphics routines pre-written in a simple, easy-to-use form. For this program, the provided mazegraphics.cpp module has functions to display a maze and highlight a path through the maze. Read the mazegraphics.h header file in the starter project for details of these functions:

• MazeGraphics::drawGrid(Grid<bool>& grid)
• MazeGraphics::highlightPath(Stack<GridLocation> path, string color)

Note that when calling these functions, you must call them using their full name (including the weird looking MazeGraphics:: prefix). We will talk more about what this notation means a little later in the quarter!

You call MazeGraphics::drawGrid once to display the maze and repeatedly call MazeGraphics::highlightPath to mark the cells along the path currently being explored. By watching this display, the user can see how the path is updated and follow along with the algorithm as it searches for a solution.

Now just sit back and watch the show as your clever algorithm finds the path to escape any maze you throw at it! 👏 Congratulations! 👏

References

There are many interesting facets to mazes and much fascinating mathematics underlying them. Mazes will come up again several times this quarter. Chapter 9 of the textbook uses a recursive depth-first search as path-finding algorithm. At the end of the quarter when we talk about graphs, we'll explore the equivalence between mazes and graphs and note how many of the interesting results in mazes are actually based on work done in terms of graph theory.

• Walter Pullen, Maze Classification. http://www.astrolog.org/labyrnth/algrithm.htm Website with lots of great info on mazes and maze algorithms
• Jamis Buck. Maze Algorithms. https://www.jamisbuck.org/mazes/ Fun animations of maze algorithms. He also wrote the excellent book about Mazes for Programmers: Code Your Own Twisty Little Passages.

Extensions

• Instead of reading pre-written mazes from a file, you could instead generate a new random maze on demand. There is an amazing (I could not resist…) variety of algorithms for maze construction, ranging from the simple to the sublime. Here are a few names to get you started: backtracking, depth-first, growing tree, sidewinder, along with algorithms named for their inventor: Aldous-Broder, Eller, Prim, Kruskal, Wilson, and many others.
• Try out other maze solving algorithms. How does BFS stack up against the options in terms of solving power or runtime efficiency? Take a look at random mouse, wall following, depth-first search (either manually using a Stack or using recursion once you get the hang of it), Bellman-Ford, or others.
• There are many other neat maze-based games out there that make fun extensions. You might gather ideas from Robert Abbott's http://www.logicmazes.com or design a maze game board after inspiration from Chris Smith on mazes.