Fractals

CS 106B: Programming Abstractions

Autumn 2020, Stanford University Computer Science Department

Lecturers: Chris Gregg and Julie Zelenski

Slide 2

Announcements

• Assignment 2 is due end-of-day today (Friday); the grace period for submission extends through end-of-day Sunday.
• Assignment 3 will be released tomorrow.

Slide 3

Observations about recursion

• The base case represents the simplest possible instance of the problem you are solving.
  • Example: How many people are behind you, including you? Answer? 1, it's just me!
  • Example: What is x^n? Answer: x^0 = 1
  • Solve the Towers of Hanoi Answer: 1 ring is easy!
• The recursive case represents how you can break down the problem into smaller instances of the same problem.
  • Example: How many people are behind you, including you? Answer? 1 + the number behind me
  • Example: What is x^n? Answer: x * x^(n-1)
  • Solve the Towers of Hanoi Answer: N-1 disks to aux, 1 disk to target, N-1 disks to target

Slide 4

Another recursion example

• Google can do arithmetic:
  • ((1*17)+(2*(3+(4*9)))) = 95

Slide 5

The Challenge

• Implement a function which evaluates an expression string:
  • "((1+3)*(2*(4+1)))"
  • "(7+6)"
  • "(((4*(1+2))+6)*7)"
  • (only needs to implement + and *)

Slide 6

Anatomy of a mathematical expression

• An expression is always one of these three things:
  • a number
  • (an expression + an expression)
  • (an expression * an expression)
• For example:
  • ((1*3)+(4*2))
    • There is an expression on the left, (1*3)
      • This expression is made up of a number * a number (and a number is also an expression)
    • There is a joining operator, +
    • There is an expression on the right, 2*4
      • This expression is made up of a number * a number (and a number is also an expression)
  • The two smaller expressions with the + joining operator make up an expression, as well.

Slide 7

Anatomy of a mathematical expression

• How do we evaluate ((1*17)+(2*(3+(4*9))))?

• First, we break each expression up into its component parts, and when we get to an expression with just numbers, we calculate those results. We have the + separating the two main expressions, (1*17) and (2*(3+(4*9)))
• Next, we start looking at the sub-expressions. The (1*17) has two numbers, so can evalute the product, to get 17. The(2*(3+(4*9))) has a number, 2 and another expression, 3+(4*9). So, we have to evaluate the non-number first.
  • We look at (3+(4*9)) and see that it has a number, 3 and an expression, 4*9, so we have to look at the expression first.
    • 4*9 has just numbers, so we can calculate the product, to get 36. Now we can back up, because we have a number for the previous expression.
  • We can calculate (3+36) to get 39, and we can move up.
• We can calculate (2*39) to get 78, and we can move up.
• Finally, we can calculate 17+78 to get 95.

Slide 8

Is it recursive? Yes!

• Take a look at ((1*3)+(4+2))
  • The big instance of this problem is the whole problem, and the smaller instances are the numbers, 1, 3, 4, and 2.
• So, we can write a recursive function:
  • int evaluate(string exp); // "((1*3)+(4+2)) returns 9
  • We can use the library functions:
    • stringIsInteger(exp)
    • stringToInteger(exp)
  • And we can use a couple of helper functions:
    • char op = getOperator(exp); // returns '+' or '*'
    • string left = getLeftExp(exp); // returns "(1*3)"
    • string right = getRightExp(exp); // returns "(4+2)"

Slide 9

Solution in Pseudocode

"((1*3)+(2*4))"

int evaluate(expression):

• if expression is a number, return expression
• Otherwise, break up expression by its operator:
  • leftResult = evaluate(leftExpression)
  • rightResult = evaluate(rightExpression)
  • return leftResult operator rightResult

Slide 10

The solution

int evaluate(string exp) {
    // base case
    if (stringIsInteger(exp)) {
        return stringToInteger(exp);
    } else {
        char op = getOperator(exp);
        string left = getLeftExp(exp);
        string right = getRightExp(exp);

        // recursive case #1
        int leftResult = evaluate(left);

        // recursive case #2 (!)
        int rightResult = evaluate(right);

        if (op == '+') {
            return leftResult + rightResult;
        } else {
            return leftResult * rightResult;
        }
    }
}

Slide 11

Helper function

int getOppIndex(string exp){
    int parens = 0; 
    // ignore first left paren
    for (int i = 1; i < exp.length(); i++) {
        char c = exp[i];
        if (c == '(') {
            parens++;
        } else if (c == ')') {
            parens--;
        }
        if (parens == 0 && (c == '+' || c == '*')) {
            return i;
        }
    }
    return -1;
}

Slide 12

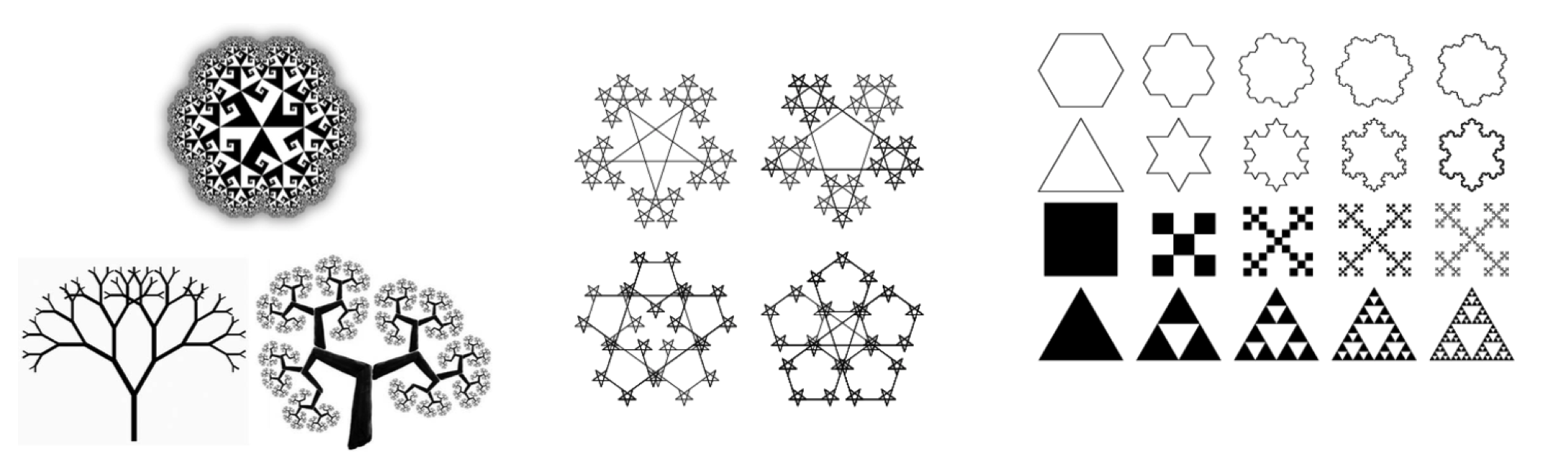
Fractals

A fractal is a recurring graphical pattern. Smaller instances of the same shape or pattern occur within the pattern itself.

Slide 13

Fractal Examples in Nature

• Many natural phenomena generate fractal patterns:
  • earthquake fault lines
  • animal color patterns
  • clouds
  • mountain ranges
  • snowflakes
  • crystals
  • coastlines
  • DNA

Slide 14

The Cantor Fractal

• We can create many fractals programmatically, and because fractals are self-similar, we can do so recursively!
• The first fractal we will code is called the "Cantor" fractal, named after the late-19th century German mathematician Georg Cantor.

• The Cantor fractal is a set of lines (indeed, a "Cantor Set" of lines) where there is one main line, and below that there are two other lines, each 1/3rd of the width of the original line, one on theleft, and one on the right (with a 1/3 separation of white space between them)
• Below each of the other lines is an identical situation: two 1/3rd lines.
• This repeats until the lines are no longer visible.

Slide 15

The Cantor Fractal

In text, a 4-level Cantor fractal would look like this:

---------------------------
---------         ---------
---   ---         ---   ---
- -   - -         - -   - -

• Parts of a cantor set image … are Cantor set images!

Slide 16

The Cantor Fractal

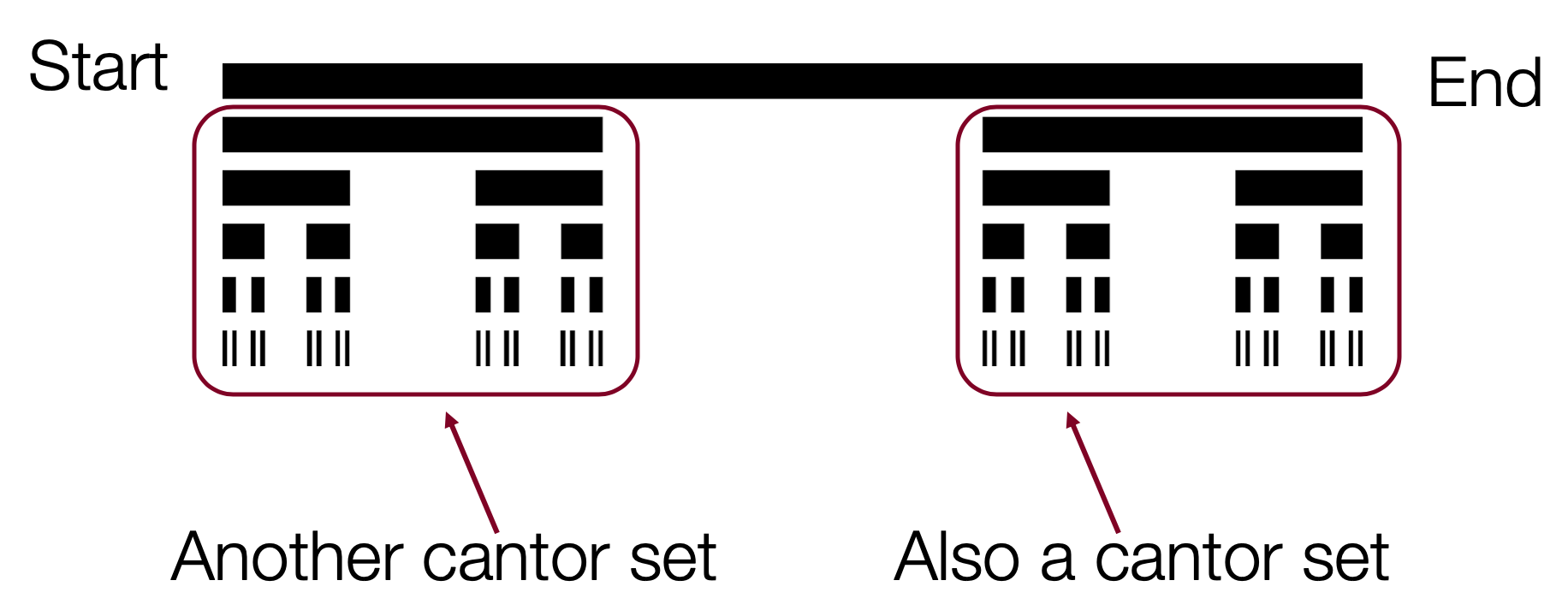
• The Cantor fractal above has six levels.
• Every individual line segment is its own 1-level Cantor fractal

Slide 17

How to draw a level 1 Cantor fractal

Slide 18

How to draw a level n Cantor fractal

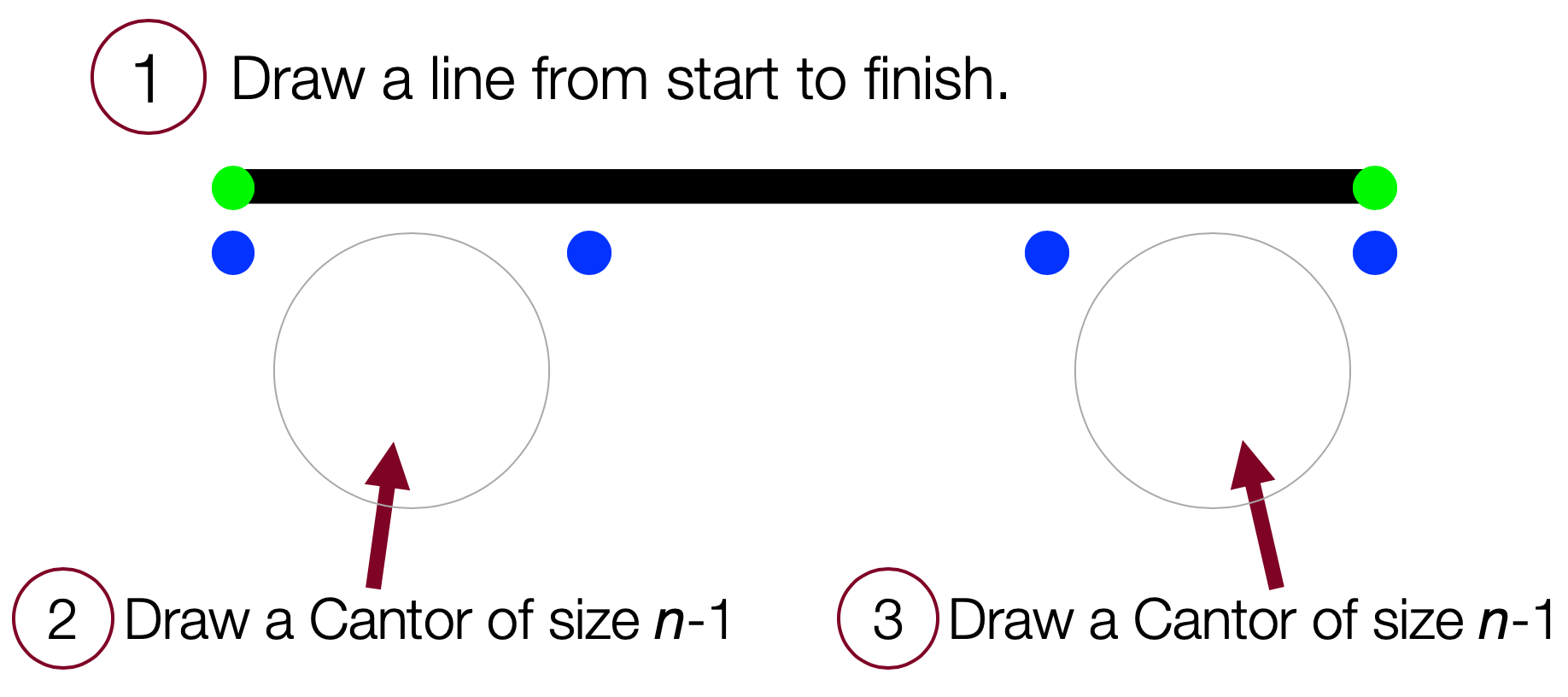
1. Draw a line from start to finish.
2. Underneath, on the left third, draw a Cantor of size n - 1.
3. Underneath, on the right third, draw a Cantor of size n - 1.

Slide 19

Graphics in C++ with the Stanford library: GPoint

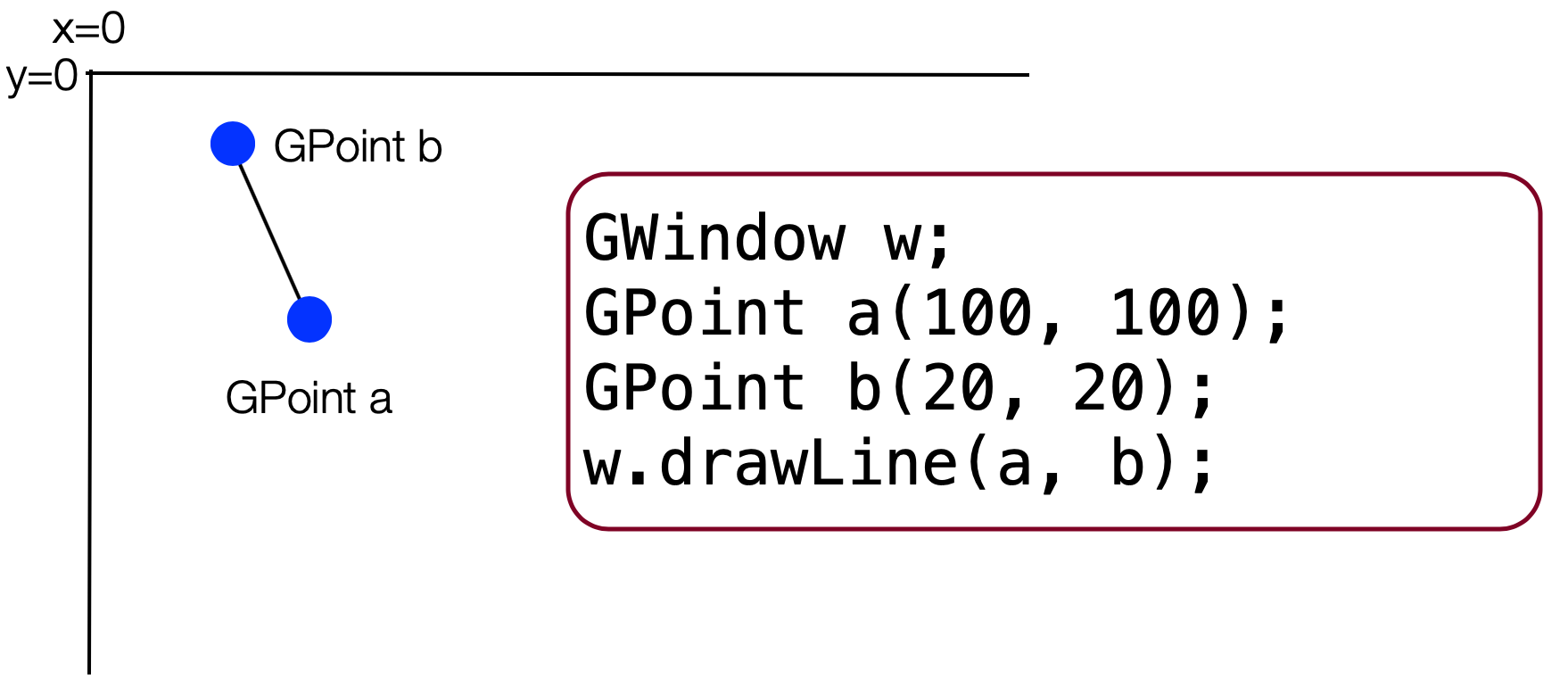
Slide 20

Let's code!

Slide 21

Snowflake Fractal

Slide 22

Let's break this down to a smaller part

Slide 23

Depth 1 Snowflake: A line

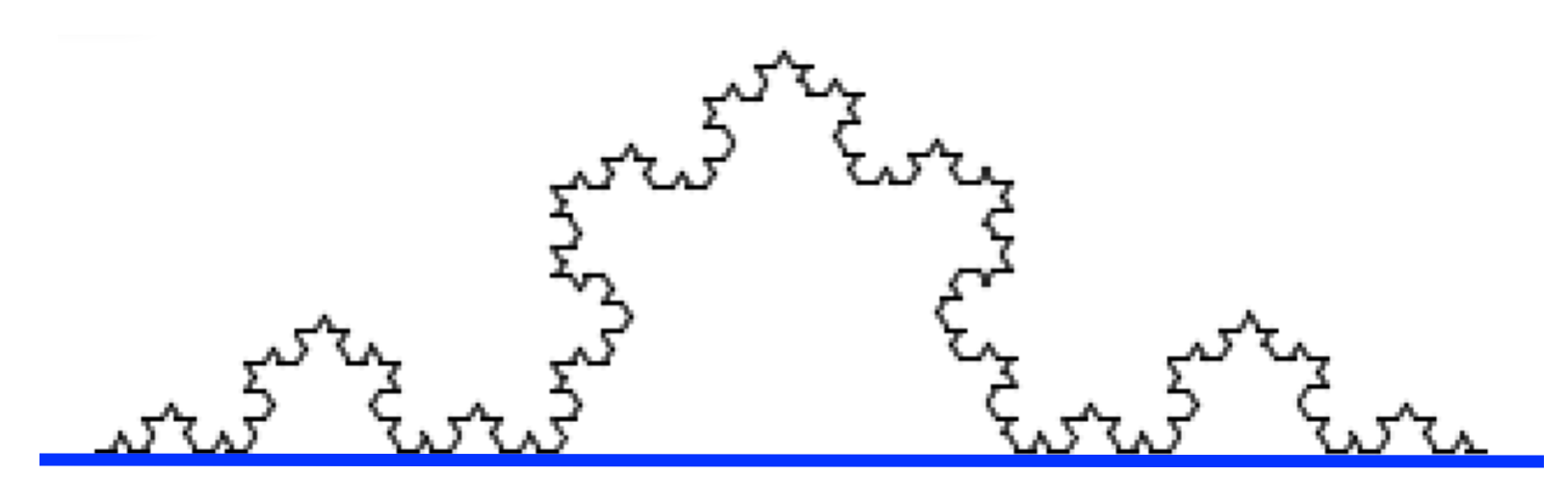
Slide 24

Depth 2 Snowflake: The line has a triangle break

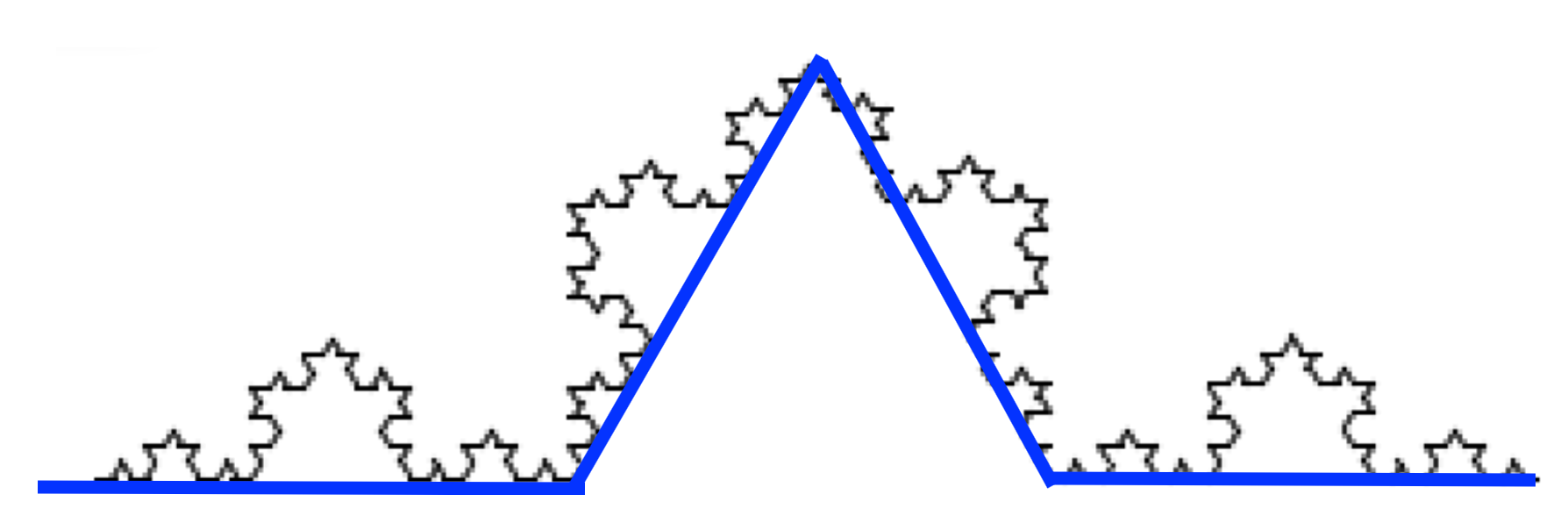
Slide 25

Depth 3 Snowflake: In progress

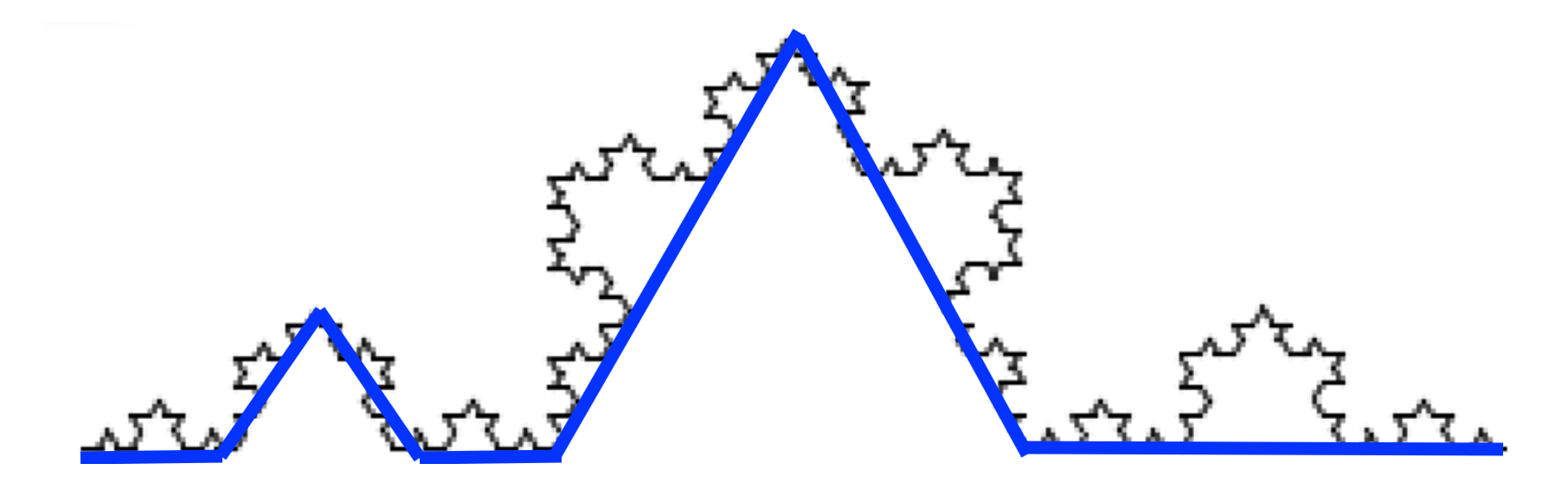
Slide 26

Depth 3 Snowflake: In progress

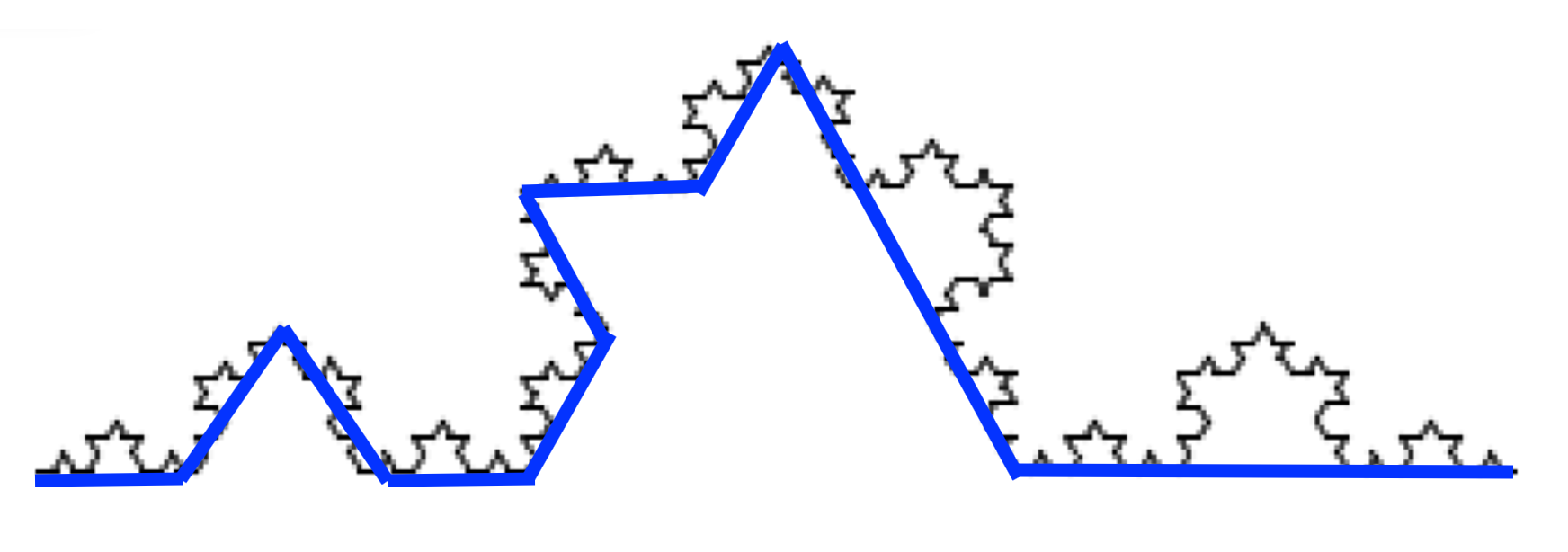
Slide 27

Depth 3 Snowflake: Finished

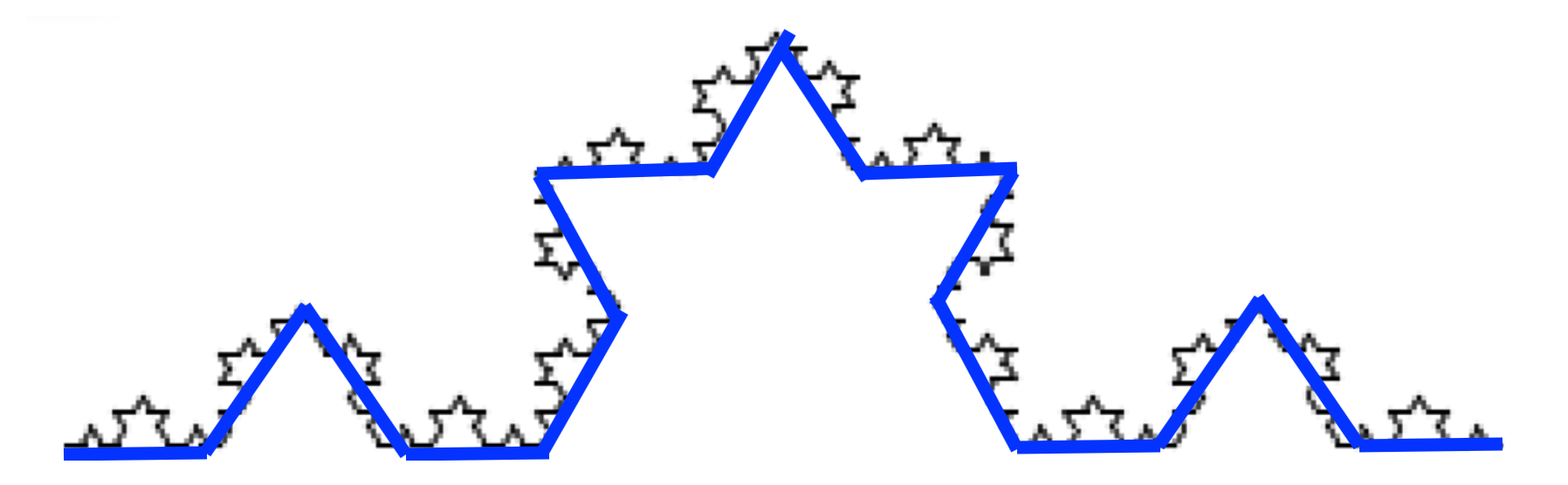
Slide 28

Let's Code a Snowflake!