Binary Heaps
CS 106B: Programming Abstractions
Autumn 2020, Stanford University Computer Science Department
Lecturers: Chris Gregg and Julie Zelenski

Slide 2
Announcements
- The mid-quarter diagnostic started early this morning at 12:01am and will be continuing on through Thursday at 11:59pm. Three important action items:
- Download BlueBook in advance of your assessment and use the Sample Exam Questions to test that you are able to successfully load a BlueBook exam file.
- When you are ready to take the diagnostic, go to the distribution portal. You should be prepared to start the diagnostic within 5-10 minutes after you get your password and
.jsonfile from that page.
- Section is still taking place normally this week.
- Assignment 5 will be released today.
Slide 3
Today's Goals:
- Introduction to Binary Heaps
- A "tree" structure
- The Heap Property
- Parents have higher priority than children
- How to add and remove from a heap?
- Heaps can be used as a priority queue
Slide 4
Binary Heaps
- A heap is a tree-based structure that satisfies the heap property:
- Parents have a higher priority than any of their children
- There are two types of heaps: a min heap and a max heap.
- A min-heap has the smallest element at the root, and a "higher priority" is a smaller number. Thus,
5is a higher priority than10.5 / \ 10 8 / \ / \ 12 11 14 13 / \ 22 43 - A max-heap has the largest element at the root, and a "higher priority" is a larger number. Thus,
50is a higher priority than19:50 / \ 19 36 / \ / \ 17 3 25 1 / \ 2 7 - We will focus mostly on min-heaps, where the lower the number means a higher priority.
Slide 5
Binary Heaps
-
There are no implied orderings between siblings, so both of the trees below are min-heaps:
5 / \ 10 12 5 / \ 12 10
Slide 6
Which of the following are min-heaps?
5
/ \
10 8
/ \ / \
12 85 14 13
/ \
22 11
13
/ \
19 36
/ \ / \
24 99 46 42
/ \
25 26
- Answer: only the second one is a heap, because in the first one, the
11is a child of the12, and therefore it breaks the heap property that a parent has to be a higher priority than its children (remember: min-heaps designate higher priority as lower numbers).
Slide 7
Binary Heaps
- Binary heaps are completely filled, with the exception of the bottom level. They are, therefore, complete binary trees:
- complete: all levels filled from left to right except the bottom
- binary: two children per node (parent)
- Maximum number of nodes
- Filled from left to right
5 / \ 10 8 / \ / \ 12 11 14 13 / \ / \ / \ / \ 22 43 __ __ __ __ __ __
Slide 8
How do you store a heap?
- It turns out that an array works great for storing a binary heap
- Later, we will see a much different approach to storing tree structures, but heaps (which also look like trees), the best solution is actually a simple array.
- The reason for this is because of the complete nature of the structure, with all levels filled from left to right.
5 / \ 10 8 / \ / \ 12 11 14 13 / \ / \ / \ / \ 22 43 __ __ __ __ __ __ - Here is the array for the above heap:
| values: | 5 | 10 | 8 | 12 | 11 | 14 | 13 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
- Notice that the array follows the levels, 5, then 10, 8, then 12, 11, 14, 13, then 22, 43 – this is the way we fill a heap.
- The array representation makes determining parents and children a matter of simple arithmetic:
- For an element at position i:
- The left child is at
2 * i + 1 - The right child is at
2 * i + 2 - The parent is at
(i - 1) / 2(integer math)
- The left child is at
heapSizeis the number of elements in the heap (for this heap,heapSizeis 9.
- For an element at position i:
Slide 9
Heap Operations
- There are three important operations in a heap:
peek(): return the element with the highest priority (lowest number for a min-heap). Don't change the heap at all.enqueue(e): insert an elementeinto the heap but retain the heap property! (we'll talk about this very soon)dequeue(): remove the highest priority (smallest element for a min-heap) from the heap. This changes the heap, and we have to return it to a proper heap.
Slide 10
Heap operations: peek()
5
/ \
10 8
/ \ / \
12 11 14 13
/ \ / \ / \ / \
22 43 __ __ __ __ __ __
| values: | 5 | 10 | 8 | 12 | 11 | 14 | 13 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
peek():- Just return the root!
return heap[0] - This is O(1) – yay, we love O(1)!
- Just return the root!
Slide 11
Heap operations: enqueue(e)
5
/ \
10 8
/ \ / \
12 11 14 13
/ \ / \ / \ / \
22 43 __ __ __ __ __ __
| values: | 5 | 10 | 8 | 12 | 11 | 14 | 13 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
- How might we go about inserting into a binary heap?
enqueue(9)into the heap above?- We have to think about this a bit. The key is to understand how heaps are built: fill each level from left to right.
- So, we start by putting the element as the left child of the 11. This probably destroys the heap property. We simply insert at
heap[heapSize]:5 / \ 10 8 / \ / \ 12 11 14 13 / \ / \ / \ / \ 22 43 9 __ __ __ __ __
values: 5 10 8 12 11 14 13 22 43 9 ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - Now, to return the structure to a proper heap, we have to do an operation called "bubble up" – we take a look at the element we just added and compare it to its parent: in this case, we look at the 9 and its parent, 11. We see that this is not proper, so we swap them:
5 / \ 10 8 / \ / \ 12 9 14 13 / \ / \ / \ / \ 22 43 11 __ __ __ __ __
values: 5 10 8 12 9 14 13 22 43 11 ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - We might not yet be done! We need to repeat the process until the element we added is either larger than its parent, or at the root. So, we compare the 9 to its new parent, the 10 (how do we know that from the array? 9 is at index 4, and (4 - 1) / 2 == 1, so we look at index 1 and find 10). Because the 9 is smaller than the 10, we have to keep bubbling up! We swap them:
5 / \ 9 8 / \ / \ 12 10 14 13 / \ / \ / \ / \ 22 43 11 __ __ __ __ __
values: 5 9 8 12 10 14 13 22 43 11 ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - We must do one more comparison, between the 9 and its new parent, the 5. Because 5 is less than 9, we're done. If we look at the heap, we can see that it is proper again.
- What is the complexity? O(log n) – yay!
- It turns out that from random inserts, the average complexity is actually O(1). See http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6312854 for details.
- See the animation at http://www.cs.usfca.edu/~galles/visualization/Heap.html
Slide 12
Heap operations: dequeue()
- How might we go about removing the highest priority (minimum)?
dequeue()5 / \ 9 8 / \ / \ 12 10 14 11 / \ / \ / \ / \ 22 43 13 __ __ __ __ __
values: 5 9 8 12 10 14 11 22 43 13 ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - We know where the minimum always is – at the root. So, we know that we will remove that element to return it. This will always destroy the heap, because it has no root!
/ \ 9 8 / \ / \ 12 10 14 11 / \ / \ / \ / \ 22 43 13 __ __ __ __ __
values: -- 9 8 12 10 14 11 22 43 13 ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - Now, what do we know about the heap after we remove an element?
- We know it will be one element smaller. Where should that element come from?
- The last level, on the right! We know this will be an empty location at the end. So, what we do (and this may be counter-intuitive) is we take that element, and we put it at the root (the heap property will almost certainly be still destroyed):
13 / \ 9 8 / \ / \ 12 10 14 11 / \ / \ / \ / \ 22 43 __ __ __ __ __ __
values: 13 9 8 12 10 14 11 22 43 ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - The next thing we do is a bubble down. We need to take the 13, and move it down.
- To bubble down, you swap the element in question with its smaller child (we have to do this because if we swapped with the larger child, we might still have a bogus heap from the root!). This means we swap the 13 with the 8, which is its smallest child:
8 / \ 9 13 / \ / \ 12 10 14 11 / \ / \ / \ / \ 22 43 __ __ __ __ __ __
values: 8 9 13 12 10 14 11 22 43 ? ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - But we're not necessarily done! We look at the 13 and its children, again, and notice that we have to swap with the smallest child, the 11:
8 / \ 9 11 / \ / \ 12 10 14 13 / \ / \ / \ / \ 22 43 __ __ __ __ __ __
values: 8 9 11 12 10 14 13 22 43 ? ? ? index: 0 1 2 3 4 5 6 7 8 9 10 11 - When we check again, we see that 13 has no more children, so we have completed the bubble down.
- What is the complexity?
- O(log n) – yay!
- Heaps are a great data structure, becuase all the operations are either O(1) or O(log n).
Slide 13
Priority Queues
- Sometimes, we want to store data in a “prioritized way.”
- Examples in real life:
- Emergency Room waiting rooms
- Professor Office Hours (what if a professor walks in? What about the department chair?)
- Getting on an airplane (First Class and families, then frequent flyers, then by row, etc.)
- A priority queue stores elements according to their priority, and not in a particular order.
- This is fundamentally different from other position-based data structures we have discussed.
- There is no external notion of "position."
Slide 14
Priority queue functions
-
A priority queue,
P, has three fundamental operations:-
enqueue(k,e): insert an elementewith keykintoP. -
dequeue(): removes the element with the highest priority key fromP. -
peek(): return an element ofPwith the highest priority key (does not remove from queue).
-
- Priority queues also have less fundamental operations:
size(): returns the number of elements inP.isEmpty(): Boolean test ifPis empty.clear(): empties the queue.peekPriority(): Returns the priority of the highest priority element (why might we want this?)changePriority(string value, int newPriority): Changes the priority of a value.
- Priority queues are simpler than sequences: no need to worry about position (or
insert(index, value),add(value)to append,get(index), etc.). - We only need one
enqueue()and onedequeue()function
Slide 15
Priority Queue Example
| Operation | Output | Priority Queue |
|---|---|---|
| enqueue(5,A) | - | {(5,A)} |
| enqueue(9,C) | - | {(5,A),(9,C)} |
| enqueue(3,B) | - | {(5,A),(9,C),(3,B)} |
| enqueue(7,D) | - | {(5,A),(9,C),(3,B),(7,D)} |
| peek() | B | {(5,A),(9,C),(3,B),(7,D)} |
| peekPriority() | 3 | {(5,A),(9,C),(3,B),(7,D)} |
| dequeue() | B | {(5,A),(9,C),(7,D)} |
| size() | 3 | {(5,A),(9,C),(7,D)} |
| peek() | A | {(5,A),(9,C),(7,D)} |
| dequeue() | A | {(9,C),(7,D)} |
| dequeue() | D | {(9,C)} |
| dequeue() | C | {} |
| dequeue() | error! | {} |
| isEmpty() | TRUE | {} |
Slide 16
Building a heap from scratch
- What is the best method for building a heap from scratch (
buildHeap())- Let's say we wanted to create a heap from: 14, 9, 13, 43, 10, 8, 11, 22, 12
- We could insert each value in turn
- An insertion takes O(log n), and we have to insert n elements, so we would have a Big O of O(n log n)
- There is actually a better way!
- Insert all elements in the order they appear, without doing any bubbling.
- Starting from the lowest completely filled level at the right-most node with children (e.g., at position n/2 - 1), bubble down each element, going backwards in the array (also O(n) to heapify the whole tree). In other words:
for (int i = heapSize() / 2 - 1; i >= 0; i--) { bubbleDown(i); }
14
/ \
9 13
/ \ / \
43 10 8 11
/ \ / \ / \ / \
22 12 __ __ __ __ __ __
| values: | 14 | 9 | 13 | 43 | 10 | 8 | 11 | 22 | 12 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
- Start with the 43, which is at
heapSize() / 2 - 1(index 3)- Bubbling it down means that the 43 swaps with the 12:
14
/ \
9 13
/ \ / \
12 10 8 11
/ \ / \ / \ / \
22 43 __ __ __ __ __ __
| values: | 14 | 9 | 13 | 12 | 10 | 8 | 11 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
- Because we are looping backwards, the next index we look at is index 2, which holds the 13.
- Bubbling it down means that the 13 swaps with the 8:
14
/ \
9 8
/ \ / \
12 10 13 11
/ \ / \ / \ / \
22 43 __ __ __ __ __ __
| values: | 14 | 9 | 8 | 12 | 10 | 13 | 11 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
-
The next index we look at is 1, and the 9 does not need to be swapped, as it is already higher priority than its children.
-
Finally, we bubble-down the 14, which needs to first swap with the 8:
8
/ \
9 14
/ \ / \
12 10 13 11
/ \ / \ / \ / \
22 43 __ __ __ __ __ __
| values: | 8 | 9 | 14 | 12 | 10 | 13 | 11 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
- We must keep bubbling down the 14, swapping it with the 11:
8
/ \
9 11
/ \ / \
12 10 13 14
/ \ / \ / \ / \
22 43 __ __ __ __ __ __
| values: | 8 | 9 | 11 | 12 | 10 | 13 | 14 | 22 | 43 | ? | ? | ? |
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
- Done!
- What is the complexity?
- Not trivial to determine, but it turns out to be O(n) (not bad!)
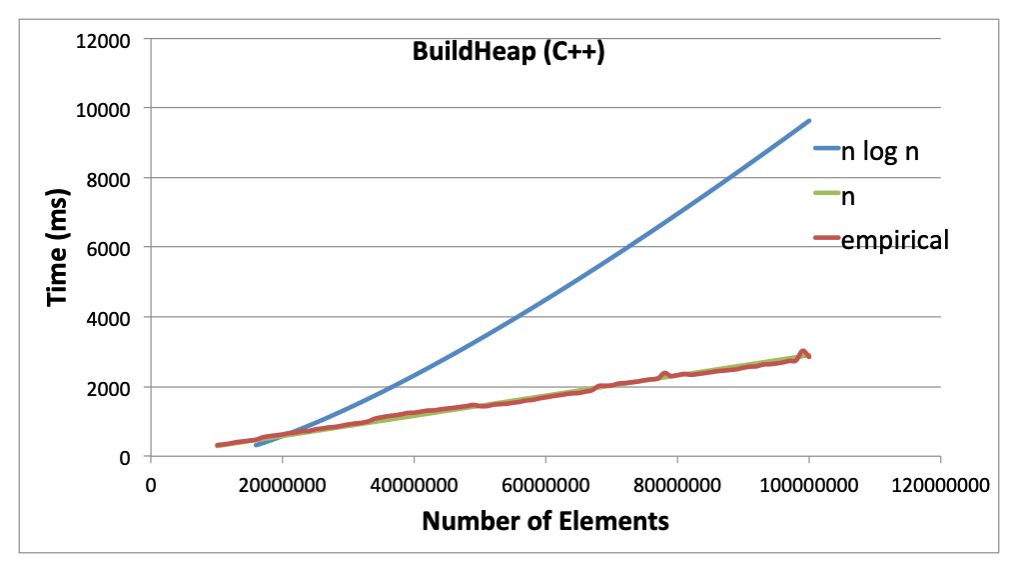
- Not trivial to determine, but it turns out to be O(n) (not bad!)