Hashing and Hash Tables

CS 106B: Programming Abstractions

Autumn 2020, Stanford University Computer Science Department

Lecturers: Chris Gregg and Julie Zelenski

A picture of delicious hashbrowns

Slide 2

Baby Binary

Slide 3

Announcements

Assignment 7 is out and due next Wednesday

Slide 4

Today's Topics

Hasham! (via Chris Piech)
Hashing
Hash Tables
Chaining
Load Factor
~~Open Addressing~~

Slide 5

Motivation

The topic we are learning about today is one of the most important topics in computer science, and it is used in many, many applications:
- Creating hash tables (which we will talk about today) that provide O(1) access for insert, find, and delete.
- Cryptography:
  - Public / Private Key Cryptography – this allows two parties to have encrypted communication without explicitly exchanging plaintext keys. It is used in every secure web page you load
  - Digitial signatures: if you want to prove a document / message / email came from a particular person, you can use public key cryptography to do so
    - Here is an exmple:
      1. Go to the download site for the latest version of Firefox.
      2. Find your version of Firefox, and download it (here is an example for a Mac).
      3. Find the SHA256 hash of the file on this page. For the file above, the hash is
        b33829c8d406a7bdf868e0e086787aff2f9cfdd5df1b7a77cff5d48e3d86bc17
      4. Check the hash of the file after you download it by running, for example, openssl dgst -sha256 ~/"Downloads/Firefox 77.0b9.dmg":
        $ openssl dgst -sha256 ~/"Downloads/Firefox 77.0b9.dmg" SHA256(/Users/tofer/Downloads/Firefox 77.0b9.dmg)= b33829c8d406a7bdf868e0e086787aff2f9cfdd5df1b7a77cff5d48e3d86bc17
      5. If the results are the same, you can be sure you've downloaded the correct file.
  - Your passwords are almost always hashed

Slide 6

Hasham! (courtesy of Chris Piech)

A stylized version of the Shazam! application logo

Let's see a demo of a very cool program, written by Chris Piech.
We will see how it is built by the end of the lecture!

Slide 7

Hashing

We have learned about many different containers this quarter:
- Vectors
- Grids
- Stacks
- Queues
- Priority Queues
- Sets / Maps using a Binary Search Tree
All of these containers have some drawbacks (and features).
- Vectors have O(n) behavior when inserting at a random location
- Grids can't be expanded easily
- Stacks, Queues, and Priority Queues can only access the top or front/back of the container
- Sets / Maps made of binary search trees have O(log n) behavior (which is very good, but not ideal)
Now, we are going to talk about another container that has find(), insert(), and remove() in O(1) (constant) time.
- The method we are going to describe is different than all the others, and is a completely different way to store keys or key/value pairs.
The method is called hashing, and to perform hashing you must have a hash function.
Some languages (like Python) use hashing as a core part of the language, and all modern languages incorporate hashing in some form.
The values returned by a hash function are called hash values, hash codes, or (simply), hashes.

Slide 8

Hashing – an introduction

Suppose we have 2-letter, lowercase words (e.g., ox or at), and their definitions.
The words are the keys, and the definitions are the values.
We want to do better (speed-wise) at storing and retrieving the keys than we can with a set (i.e., better than O(log n)).
Consider this:
- Because there are 26 letters in the English alphabet, and we have two-letter words, we have a total of 26 * 26 = 676 different possibilities for the words. I.e., aa, ab, ac, … zx, zy, zz. Some aren't words, of course, but let's assume we want the ability to store all two-letter combinations.
- Where could we store the 676 words? How about in an array? We'll say that the array has buckets for each key.
- We are going to call this array a hash table.

Slide 9

Our first hash function

If we want to put our 2-letter words into the array in an organized way, we can do so with a bit of arithmetic.
- Let's treat the letters as if they were digits in a base 26 system: Each character is assigned a value from 0 to 25, and the first character in the word will be worth 26 times its value, and the second character will be worth its value. To get the array index, we add the two together. Here are two examples:


    
        values (ints):
        a
        b
        c
        d
        e
        f
        g
        h
        i
        j
        k
        l
        m
        n
        o
        p
        q
        r
        s
        t
        u
        v
        w
        x
        y
        z
    
    
        index:
         0 
         1 
         2 
         3 
         4 
         5 
         6 
         7 
         8 
         9 
         10 
         11 
         12 
         13 
         14 
         15 
         16 
         17 
         18 
         19 
         20 
         21 
         22 
         23 
         24 
         25

ox = (14 * 26) + (23 * 1) = 387
at = (0 * 26) + (19 * 1) = 19

Here is our hash function in C++:

int hashWord(string word) {
    return (word[0] - 'a') * 26 + (word[1] - 'a'); 
}

Here is how we define the array to hold the hash table:
```
string* table = new string[676];
```

Now, we can store the definition for the words in the hash table at the location we get from the hash function:

string key1 = "ox";
string value1 = "a domesticated bovine animal";

string key2 = "at";
string value1 = "expressing location or arrival in a particular place or position.";

table[hashWord(key1)] = value1; // will go into index 387
table[hashWord(key2)] = value2; // will go into index 19

Slide 10

Definition of a hash function

Here is a good first definition of a hash function:

Any algorithm that maps data to a number, and that is deterministic.

Does our hash function fit this definition?

int hashWord(string word) {
    return (word[0] - 'a') * 26 + (word[1] - 'a'); 
}

It does – we get a number, and that number will always be the same for a particular input (i.e., ox will always produce 387, and at will always map to 19).
Why does this help us with O(1) access?
- It takes constant time to run the hash function, and constant time to insert into the array.
  - It also takes constant time to find, and constant time to delete (no moving necessary – just put an empty string to delete a value).
- We did it!
  - Well…wait a minute…

Slide 11

Hashing – all words?

We only built our table for 2-letter words.
What if we wanted to store all English words?

Word	Letters	Characteristics
Methionylthreonylthreonylglutaminylarginyl...isoleucine	189,819	Chemical name, disputed...
Methionylglutaminylarginyltyrosylglutamyl...serine	1,909	Longest published word
Lopadotemachoselachogaleokranioleipsano...pterygon	183	Longest word coined by a major author
Pneumonoultramicroscopicsilicovolcanoconiosis	45	Longest word in a major dictionary
Supercalifragilisticexpialidocious	34	Famous for being created for Mary Poppins
Pseudopseudohypoparathyroidism	30	Longest non-coined word in a major dictionary
Floccinaucinihilipilification	29	Longest unchallenged nontechnical word
Antidisestablishmentarianism	28	Longest non-coined and nontechnical word
Honorificabilitudinitatibus	27	Longest word in Shakespeare's works; longest word in the English language featuring alternating consonants and vowels.

Slide 12

What if we wanted to store all words?

An image of a place in New Zealand with the name Taumatawhakatangihangakoauauotamateaturipukakapikimaungahoronukupokaiwhenuakitanatahu

The image above is of a hill in New Zealand called "Taumatawhakatangihangakoauauotamateaturipukakapikimaungahoronukupokaiwhenuakitanatahu".
The name supposedly means

The summit where Tamatea, the man with the big knees, the climber of mountains, the land-swallower who traveled about, played his nose flute to his loved one.

Slide 13

Hashing long words

What if we wanted to hash Supercalifragilisticexpialidocious using our hashing method?
- We would need an array with 26^34 buckets – way, way too many! (26^36 ≅ 10^48, or about the number of iron atoms in the Earth. 16GB of memory is roughly 10^10 bytes, meaning that you would need 100 billion, billion, billion times more memory to hold that one array).
- English has about 700,000 words
- The array we would need would not only be enormous, but it would also end up being amazingly sparse. Each word would be, on average, 1.8 x 10^42 buckets apart (though it would be heavily shifted towards the left, because most words are short).
We need to conserve space
- For a 700,000 word dictionary, we really only want 700,000 spots (or even smaller, if we only want a subset of the words).
A better definition of a hash function would be this:

Any algorithm that maps data to a number, that is deterministic, and that maps to a fixed number of locations.
But remember, we need to be able to store arbitrary words (i.e., we could add any word, of any length with the characters in our dictionary!)

Slide 14

How to hash to a fixed number of buckets

A good method for mapping to a fixed number of locations is to use the modulus operator:
```
h(hashCode) = hashCode mod N
```
Where N is the length of the array we want to use.
Once we do this, we say we have compressed the hash, with a compression function.
- Technically, the function that creates the hash is the prehash function.
Using this compression function, we now have the ability to create a proper hash table.
- A hash table maps a huge set of possible keys into N buckets by applying a compression function to each hash code.

Slide 15

Hashing You!

Hash codes must be deterministic.
Hash codes should be fast and distributed

We have the following:

     prehash                 compression 
key --------->  hash code  -------------->  [0, N-1]

Now, let's hash you!
- We will do this via Zoom polls
- There are ten different choices, 0 - 9
- Based on the hash functions below (one at a time), choose the bucket you will land in.
- For example, for the "decade of your birth year", if you were born in the 1990s, you would choose (1990 / 10) % 10, or bucket "9". If you were born in 2000-2009, you would choose bucket 0, or (2000 / 10) % 10 = 200 % 10 = 0.
- We are going to hash you based on your birthday, in four different ways:
  1. by the decade of your birth year: (year / 10) % 10
  2. by the last digit of your birth year: year % 10
  3. by the last digit of your birth month: month % 10
  4. by the last digit of your birth day: day % 10

Slide 16

Birthday hashing

There were some problems with the birthday hashing!
- Lots of people ended up in the same bucket
  - This is called a "collision" – if we had only allowed one person per bucket, we would have been in trouble
- The distribution wasn't always great
Although we will still have collisions (we will deal with them shortly), we should pick the number of buckets at about the same size as the number of elements we want to hash. In other words:
- n is the number of keys we want to store
- N is the number of buckets in the table
- We want to make n approximately equal to N. We will discuss why shortly.

Slide 17

Collisions

With our hash/compression functions, we will ultimately have to deal with collisions, where we map the same key to the same bucket:
```
h(hashCode1) == h(hashCode2)
```

Let's do an example.

Let's say we have an array of 10 buckets. Empty locations will have -1 (we will only add positive values).
The keys will be integers
hashCode(k) = k % 10
We first want to insert 7, 8, 41, and 34

The insertions are straightforward:

How do we find(k) the keys once they are in the table?
- Easy! We hash/compress the key again, and then access the table. E.g., hashCode(34) == 4, and we access table[4] to see if the key is there.
Can we perform findMax(k) or findMin(k)
- No! We would have to search the entire table. This is a limitation of hash tables.

What if we now try to add 54?

We can't have two keys sharing the same bucket, so we have a collision

Slide 18

Hash table chaining

A set of links from a metal chain

To handle collisions in a hash table, there are a few options.

The option we will discuss today is called chaining, where each bucket has a linked list of entries, called a chain.

In other words, instead of storing integers, we store a pointer to a linked list, which stores integers.
When we find the bucket for a key, we have to search through the linked list to find the key (which means that we must store the keys and values in the linked list).


    
        
        0
        1
        2
        3
        4
        5
        6
    
    
        table →
        
        
        X
        
        X
        X
        
    
    
        
        ↓
        ↓
        
        ↓
        
        
        ↓
    
    
        
        key:novel
val:book
        key:swirl
val:spiral
        
        key:cat
val:mammal
        
        
        key:hint
val:word invented by Shakespeare
    
    
        
        ↓
        
        
        ↓
        
        
        
    
    
        
        key:supercalifragilistic-
expialidocious
val:song
        
        
        key:ox
val:bovine

Slide 19

Limiting the size of the linked list

With this linked list chaining idea, we have to be careful that we don't make the lists too long.
- If the list lengths become relevant with respect to n (the number of keys in the hash table), then our hash table becomes O(n), which is bad!
- As noted before, we want the number of buckets, N, to be about the same size as the number of elements, n. We can quantify this using the idea of the load factor, defined as follows:
```
               n
Load Factor = ---
               N
```
If
- the load factor stays low (generally below 1.0), and
- the hash code and compression function are good (we will see what this means), then
- each operation takes O(1) time!
However, if
- the load factor gets big (n >> N), then
- each operation takes O(n) time.
If the load factor gets too big, move your hash table to a bigger array.
- How do we move a hash table?
  - We have to go through the entire table and re-hash all keys to the new table (this is a big penalty, but worth it to keep the load factor low).

Slide 20

Hash Codes and Compression Functions

We said that
- Hash codes must be deterministic
- Hash codes should be fast to create and distributed
An ideal hash would map each key to a random bucket.
Is an ideal hash collision-free?
- What does your intuition say about 2,500 randomly placed keys in 1,000,000 buckets? How likely is a collision?
- We can test this! (run this code)

Solution

Even an ideal hash will not remove all collisions:

if 2,500 keys are hashed into a million buckets, even with a perfectly uniform random distribution, according to the birthday problem there is a 95% chance of at least two of the keys being hashed to the same slot. [Wikipedia, Hash Table]

Slide 21

What makes a good or bad compression function?

A bad compression function example:
- Suppose the keys are ints
- hashCode(i) = i; // hashCode is itself
- Compression function: h(hashCode) = hashCode % N
- N = 10,000 buckets
- Suppose the keys are divisible by 4
  - N is also divisible by 4
  - This is bad news, as 3/4 of the buckets are never used (not well distributed)
- One fix: make N prime. Now, when you take % N, the numbers are not divisible by any number in particular.
- Here is a better compression function:
```
h(hashCode) = ((a * hashCode + b) % p) % N
```
- a, b, and p are positive integers
- p is a large prime number and p >> N. p scrambles the bits nicely
- Now you don't have to worry about the number of buckets being prime.

Slide 22

A good hash function for strings

The following is a decent hash function for strings:

const int P = 16908799;
int hashCode(string key) {
	  int hashVal = 0;
	  for (int i = 0; i < key.length(); i++) {
	     hashVal = (127 * hashVal + key[i]) % P;
	  }
	  return hashVal;
}

This function sufficiently scrambles the bits such that it does a good job randomizing the output. E.g.:

hashCode("a") = 97
hashCode("ab") = 12417
hashCode("abc") = 1577058
hashCode("abcd") = 14289677
hashCode("abcde") = 5547587
hashCode("abcdef") = 11282892
hashCode("Stanford") = 10895896
hashCode("STANFORD") = 5472097

A bad hashcode for strings would be something like this:
- Sum the ASCII values of the characters
This function rarely exceeds 500 for a word
Most words would be bunched up into 500 buckets
Anagrams always collide

Slide 23

Back to Hasham

A stylized version of the Shazam! application logo

Hasham requires a large search space (source: Wang., A. An Industrial-Strength Audio Search Algorithm)
Do you recognize this song? (probably not…)
If you discretize the plot, you can pick out frequencies that occur at particular times in a song.
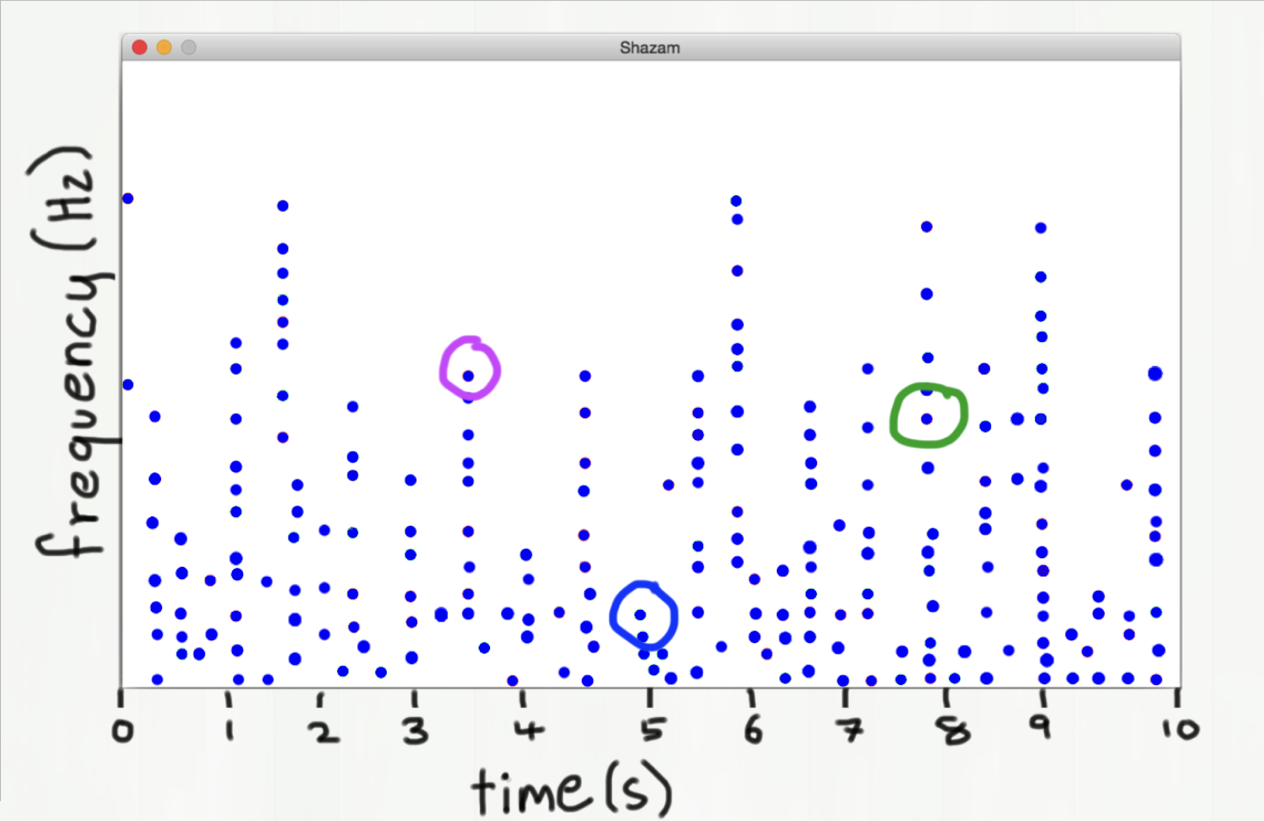
We don't hash the entire song (that would take too much time and memory)
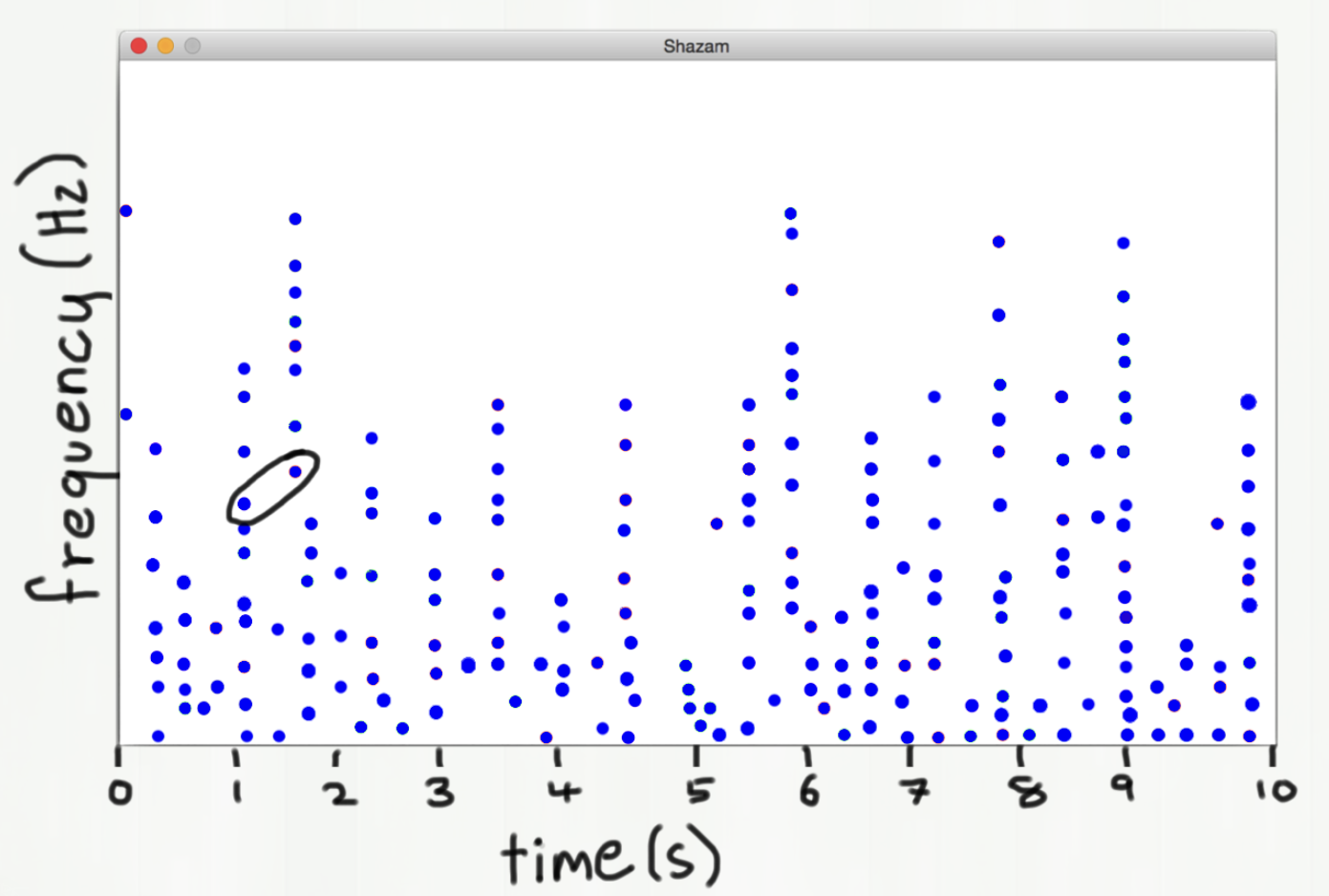
- Instead, we look at pairs of notes that occur near each other in time.
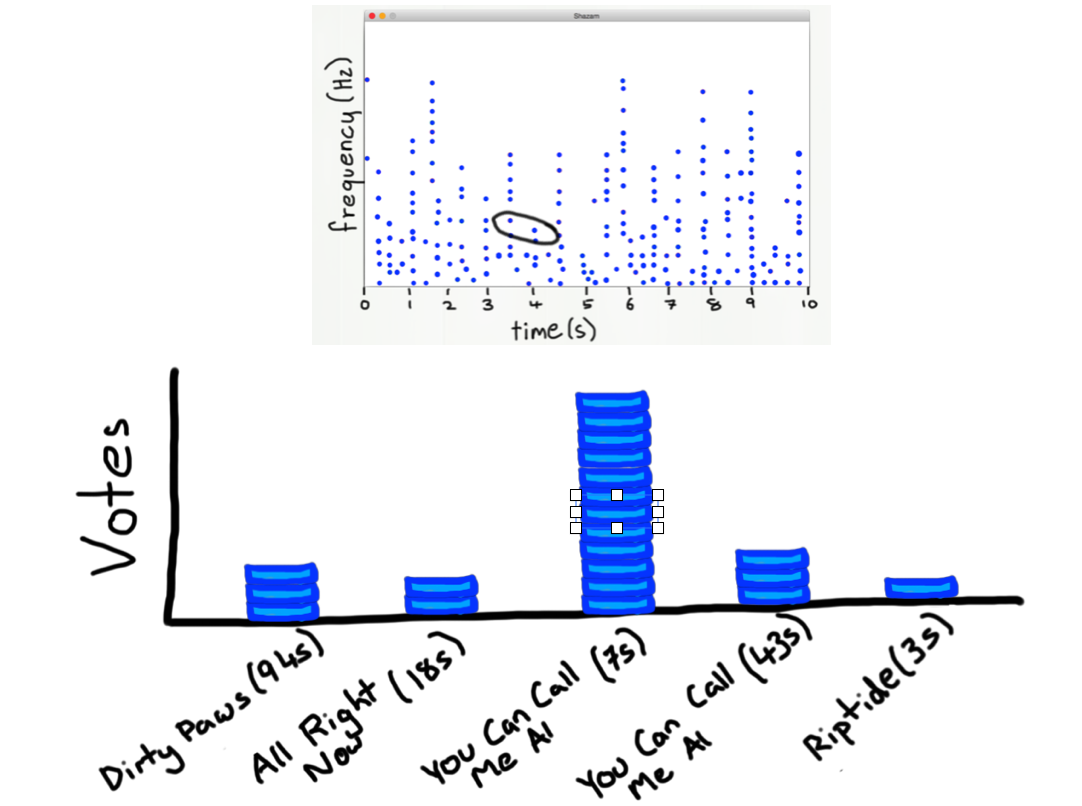
For every pair found in a song, that counts as a vote for the song. The song with the most votes is the most likely song:

We can write a little hash function based on the two frequencies and the time difference:

int hash(int f1, int f2, int timeDelta) { 
    int p = 31; 
    int pre = f1 + (p * f2) + (p * p * timeDelta); 
    return pre % NUM_BUCKETS; 
} 

values (ints):	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	p	q	r	s	t	u	v	w	x	y	z
index:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25

	0	1	2	3	4	5	6
table →			X		X	X
	↓	↓		↓			↓
	key:novel val:book	key:swirl val:spiral		key:cat val:mammal			key:hint val:word invented by Shakespeare
	↓			↓
	key:supercalifragilistic- expialidocious val:song			key:ox val:bovine