Introduction to Graphs

CS 106B: Programming Abstractions

Autumn 2020, Stanford University Computer Science Department

Lecturers: Chris Gregg and Julie Zelenski

A simple graph with six vertexes, numbered 1-6. 6 has a single edge to 4. 4 has edges to 3, 5, and 6. 5 has edges 4 and 2. 2 has edges to 3, 1, and 5. 2 has edges to 1, 3, and 5. 1 has an edge to 2.

Slide 2

Announcements

  • Assignment 7 is due on Wednesday at 11:59pm
  • The last section is this week!
  • Make sure you start working on your project write-up, which will be due on Sunday, November 15th, 11:59pm. This hard deadline with no grace period.
  • Next week you will present your projects to your SL.

Slide 3

Today's Topics

  • Graphs - the wild west of the node-based world
  • How graphs are used for real-world problems
    • Map direction-finding
      • Dijkstra's algorithm
      • A* Algorithm
    • Internet routing and traceroute
    • Social networks
    • Product relationships (e.g., on Amazon)
    • Routing circuits

Slide 4

Graph Motivation 1

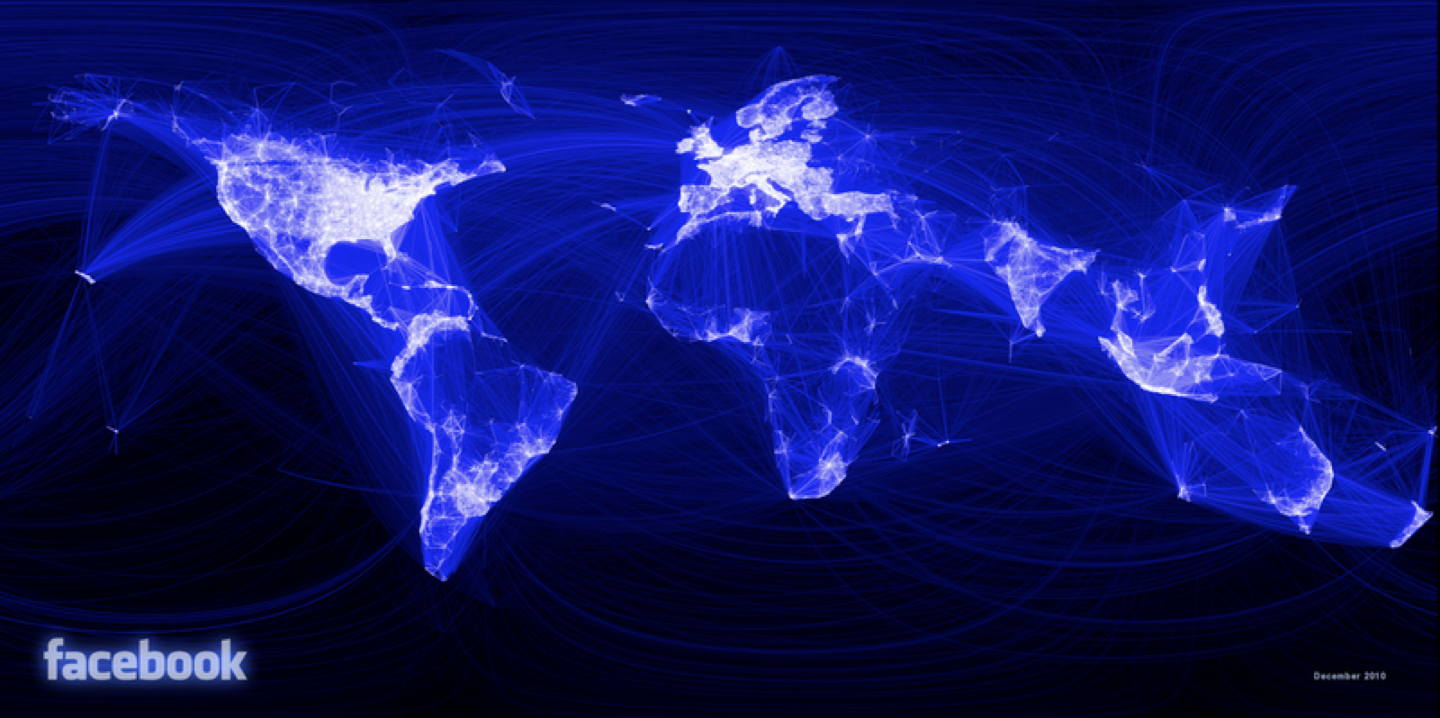
A map of the world showing Facbook connections. The map was drawn only using the connections, in other words, the outline of the countries only comes from the fact that there are people connected via facebook living there

  • Have you ever heard of a little company called Facebook? How about LinkedIn?
    • Companies that connect people together use a social graph to do so. Facebook has the world's largest social graph, connecting well over a billion people together. Facebook keeps track of connections in a graph data structure, which we will discuss today.

Slide 5

Graph Motivation 2

  • Have you ever wondered how your computer connects to other computers around the world?
  • You can see how this works with the traceroute command (Mac/Linux) or the tracert command (Windows).
  • Let's look at connecting from Stanford to the University of New South Wales, in Australia: 
    $ traceroute www.engineering.unsw.edu.au
traceroute to www.engineering.unsw.edu.au (149.171.158.125), 30 hops max, 60 byte packets
 1  csee-west-rtr-vl3804.SUNet (171.67.64.2)  0.296 ms  0.287 ms  0.275 ms
 2  xb-nw-rtr-vlan2.SUNet (171.64.255.130)  0.441 ms  0.419 ms  0.413 ms
 3  hpr-svl-rtr-vlan3.SUNet (171.66.255.147)  1.007 ms  0.997 ms  0.985 ms
 4  hpr-svl-hpr3--stan-100ge.cenic.net (137.164.27.60)  1.024 ms  1.013 ms  1.045 ms
 5  aarnet-2-is-jmb-778.sttlwa.pacificwave.net (207.231.245.4)  18.490 ms  18.486 ms  17.747 ms
 6  et-2-0-0.pe1.a.hnl.aarnet.net.au (113.197.15.200)  71.593 ms  70.828 ms  70.816 ms
 7  et-2-1-0.pe1.sxt.bkvl.nsw.aarnet.net.au (113.197.15.98)  164.803 ms  164.611 ms  163.838 ms
 8  et-3-3-0.pe1.brwy.nsw.aarnet.net.au (113.197.15.148)  163.997 ms  163.169 ms  163.981 ms
 9  138.44.5.1 (138.44.5.1)  163.384 ms  164.376 ms  163.513 ms
10  libcr1-te-1-5.gw.unsw.edu.au (149.171.255.102)  164.283 ms  165.070 ms  164.893 ms
11  libdcsl1-swp-5.gw.unsw.edu.au (149.171.255.174)  164.322 ms ombdcsl1-swp-5.gw.unsw.edu.au (149.171.255.194)  164.923 ms libdcsl1-swp-5.gw.unsw.edu.au (149.171.255.174)  164.380 ms
12  srdh5it8r22blfx1-ext.gw.unsw.edu.au (129.94.0.32)  163.981 ms srdh4it2r26blfx1-ext.gw.unsw.edu.au (129.94.0.31)  165.176 ms  165.102 ms
13  dcfw1-ae-1-3065.gw.unsw.edu.au (129.94.254.76)  164.405 ms  164.210 ms  165.111 ms
14  engplws011.ad.unsw.edu.au (149.171.158.125)  165.852 ms  164.604 ms  165.161 ms
  • It takes three hops just to get out of Stanford University. This is because there are a lot of computers at Stanford, and many smaller networks inside the school.
  • After the first three hops, we get to a site called cenic.net. This is the Corporation for Education Network Initiatives in California (CENIC), a nonprofit corporation formed in 1996 to provide high-performance, high-bandwidth networking services to California universities and research institutions (source: Wikipedia)
  • After that the next hop is to sttlwa.pacificwave.net, whose job is "to pass Internet traffic directly with other major national and international networks, including U.S. federal agencies and many Pacific Rim R&E networks" The logo for Pacific Gigapop, Northwest
  • The world's first undersea cables were in the 1850s (!) in the U.K. (under the English Channel) and linking non-land-locked countries in Europe. They were used to send Morse code.
  • The first Transatlantic cable that was successful was laid in 1865, with 2300 miles of cable spools, laid from England to Newfoundland.
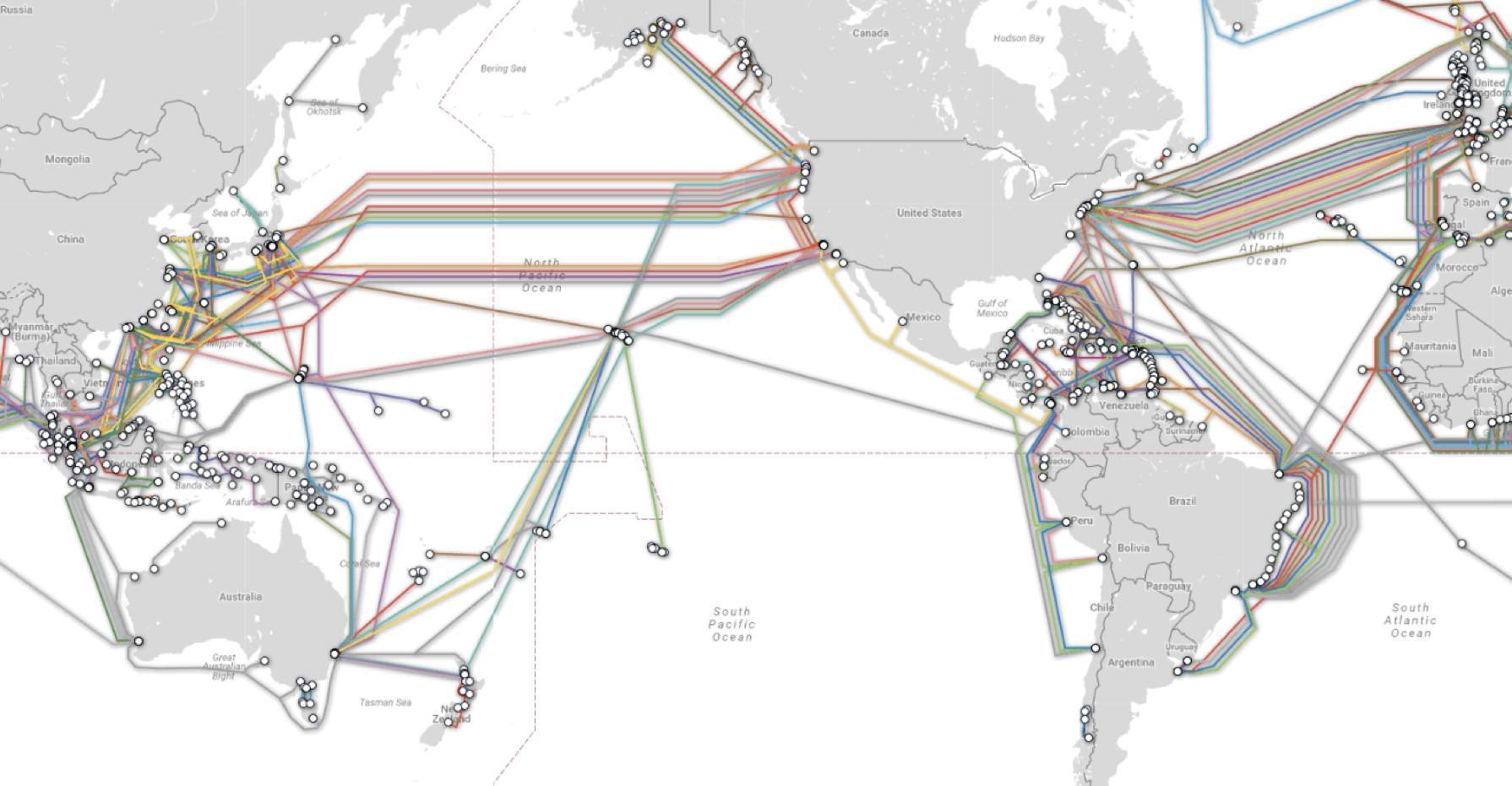
  • The next stop is Australia! How does this happen? Under the sea! A map of the world's undersea cables
  • Once the route gets to Australia, it takes four more hops to get to the University of New South Wales, and then four more hops to get to the computer I finally wanted to get to, in the engineering department.
  • The time to get to the final computer is 165 milliseconds.
  • Why don't we just use satellites?
    • Reason 1: Expense–satellites are so expensive, that it is cheaper to lay actual cable under the ocean.
    • Reason 2: Time–most communications satellites are in geostationary orbit, 22,236 miles away from Earth. Because of speed-of-light limitations, it takes almost 1/8th of a second (120ms) to get a signal from Earth to the satellite, and another 1/8th of a second to get back. This means that the total round-trip time is at least 240ms, which is slower than an undersea cable, which has to to less than 10,000 miles (instead of over 40,000 miles)
    • Reason 3: Bandwidth–modern undersea cables use fibre-optic cables, which can transmit a tremendous amount of data quickly. Satellites have limited bandwidth and cannot compete.
  • The bottom line (no pun intended): computer networks are graphs, and managing these graphs enable us to connect the world's computers together.
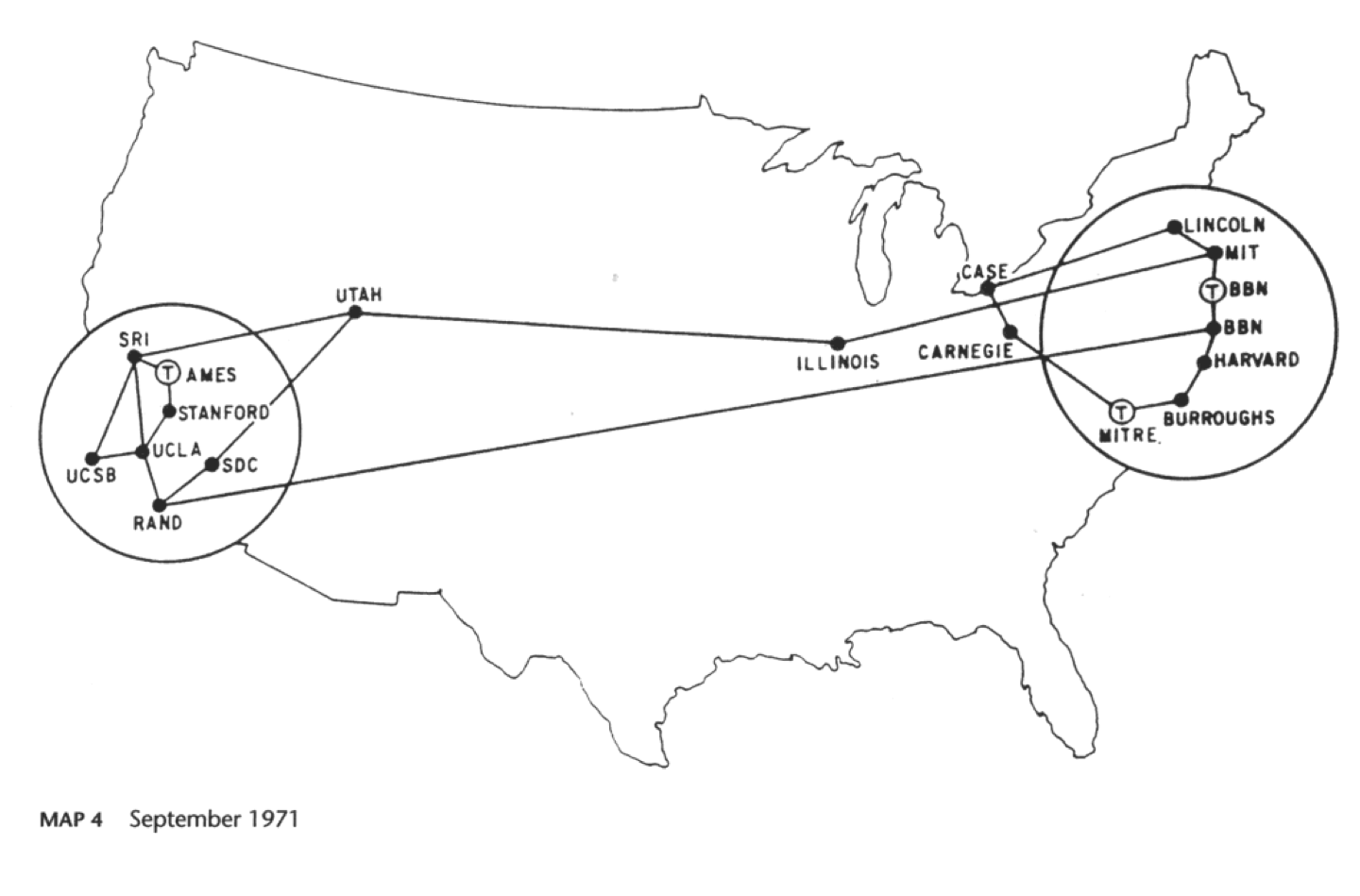
  • Originally, the Internet was only a few nodes: A map of the Internet in 1971
  • Today's Internet has 20 billion+ nodes: A map of the Internet

Slide 6

Graph definition

  • This was our tree definition: An image of a real parent holding a child's hand, and an image of a bicycle with a red 'no' sign through it

  • Now that we are talking about graphs…

An image of Morpheus from the Matrix movie, saying 'What if I told you there were no rules?'

  • A graph is a mathematical structure for representing relationships using nodes and edges.
  • This is just like a tree, but without any rules! I like to call graphs the wild west of the node-based world.
  • With graphs, we don't have any more notion of parents and children, and we allow cycles.

Slide 7

Graphs can have cycles

  • Graphs do not have any notion of a parent-child relationship, and they can have cycles: A simple graph with six vertexes, numbered 1-6. There is a cycle from 4-5-2-3, which means that you can continue from the 3 back to the 4, and go in the cycle continuously. 6 has a single edge to 4. 4 has edges to 3, 5, and 6. 5 has edges 4 and 2. 2 has edges to 3, 1, and 5. 2 has edges to 1, 3, and 5. 1 has an edge to 2.

Slide 8

Graphs do not have roots

  • Graphs also do not have roots: A graph from the show Game of Thrones -- Catelyn has a directed edge to Tyrion, and The High Sparrow has a directed edge to Tyrion. Tywin has directed edges to Tyrion, Cersi, and Jaime. Cersi has a directed edge to Joffrey, and Jaime also has a directed edge to Joffrey
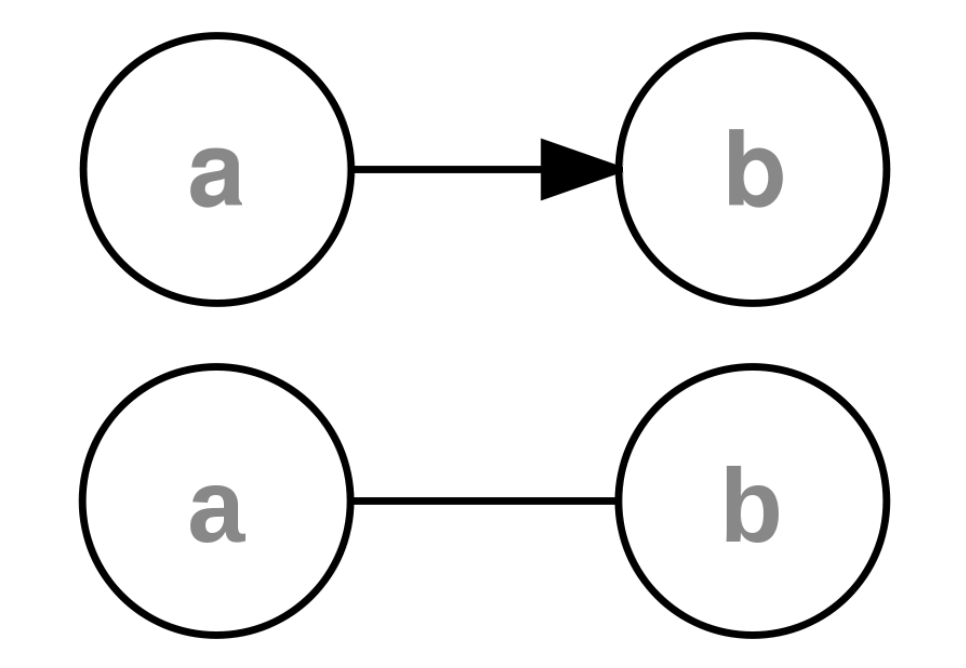
  • Notice that graphs can also have directed edges, which means that you can get from one node to another but not necessarily in the other direction: Two graphs with A and B nodes. In the first, there is an arrow point going from a to b, meaning the graph has directed edges and going from a to be is possible, but not b to a. In the other graph, there is just a line between a and b, so it is bi-directional

Slide 9

Weighted Graphs

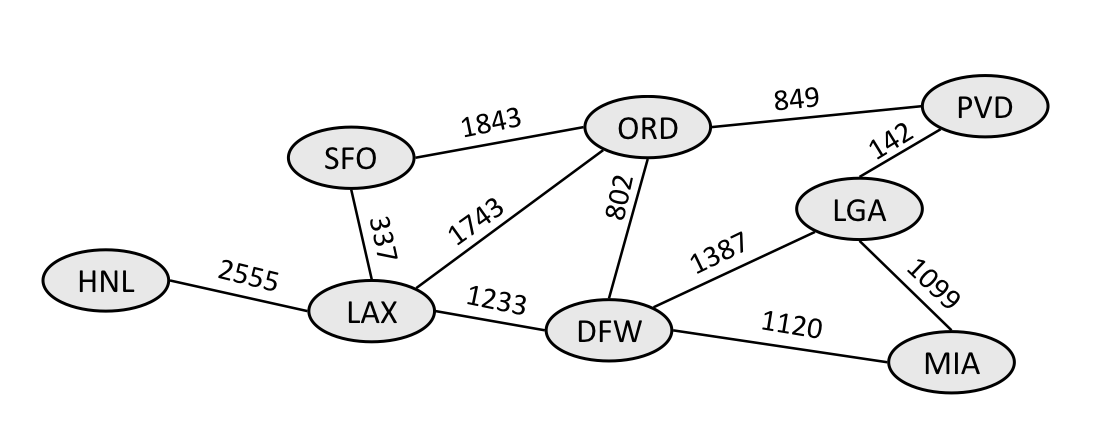
  • A graph is considered weighted if it has numbers associated with edges. Weighted graphs are particularly useful for applications such as mapping between two locations, to take into consideration traffic, distance, time, etc.
  • This is an example weighted graph of airline flights, with the weights representing the miles between airports. A weighted graph of airports with mileage distances between each airport and the ones they connect to. E.g., SFO connects to LAX with 337 as its weight, and SFO also connects to ORD with 1843 as its weight. ORD connects to LAX (1743), SFO, DFW (802), and PVD (849)

Slide 10

Different types of graphs: prerequisite graph

  • Graphs can also represent prerequisites: A graph of 'prerequisites' for learning C++. fractals has a directed edge to recursion which has a directed edge to collections and another to function calls, and function calls has a directed edge to simple c++.

Slide 11

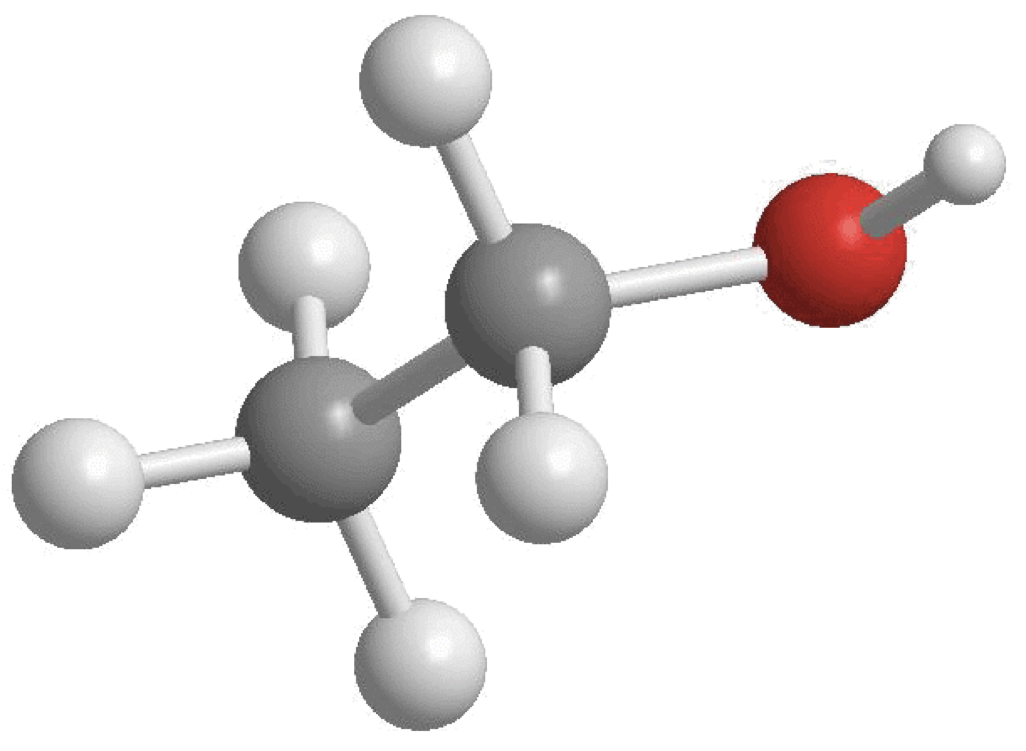
Different types of graphs: chemical bonds

  • A graph can be used to represent chemical bonds (even the drawings you are familiar with have nodes and edges). Ethanol is shown below: A graph of a chemical bond of ethanol

Slide 12

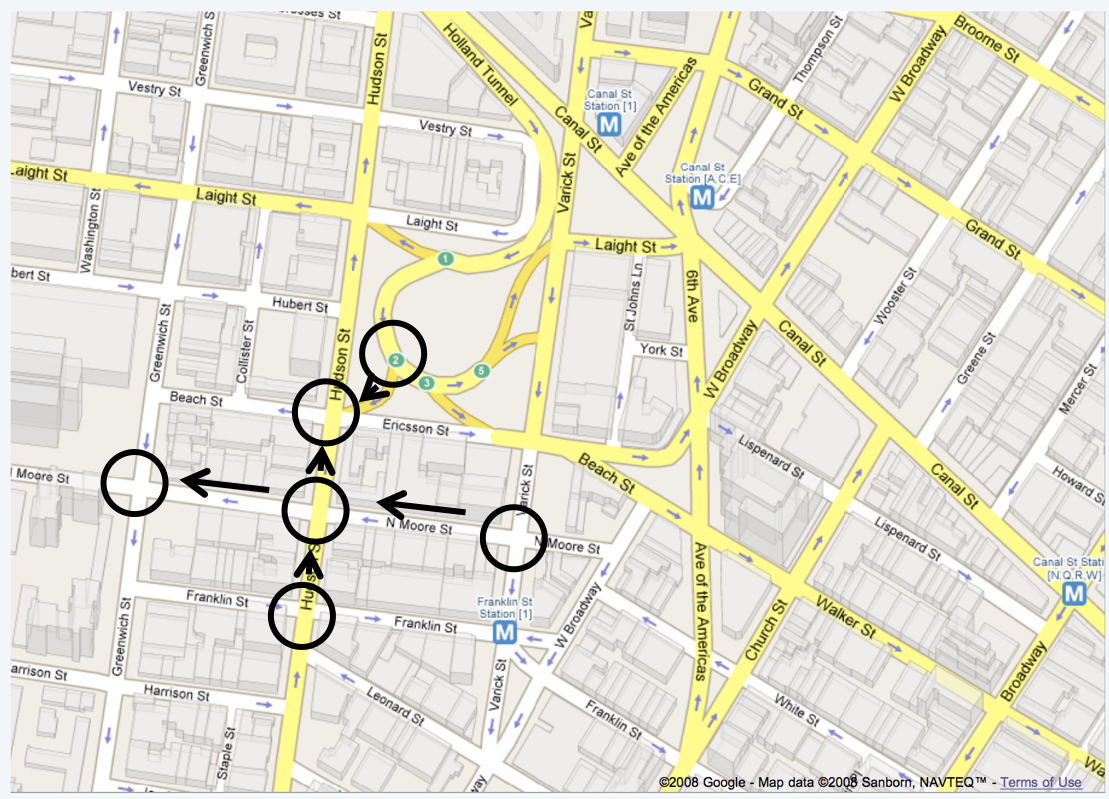
Different types of graphs: road maps

  • A graph can be used to represent road maps, which is particularly effective for applications such as Google Maps: A graph of a road map

Slide 13

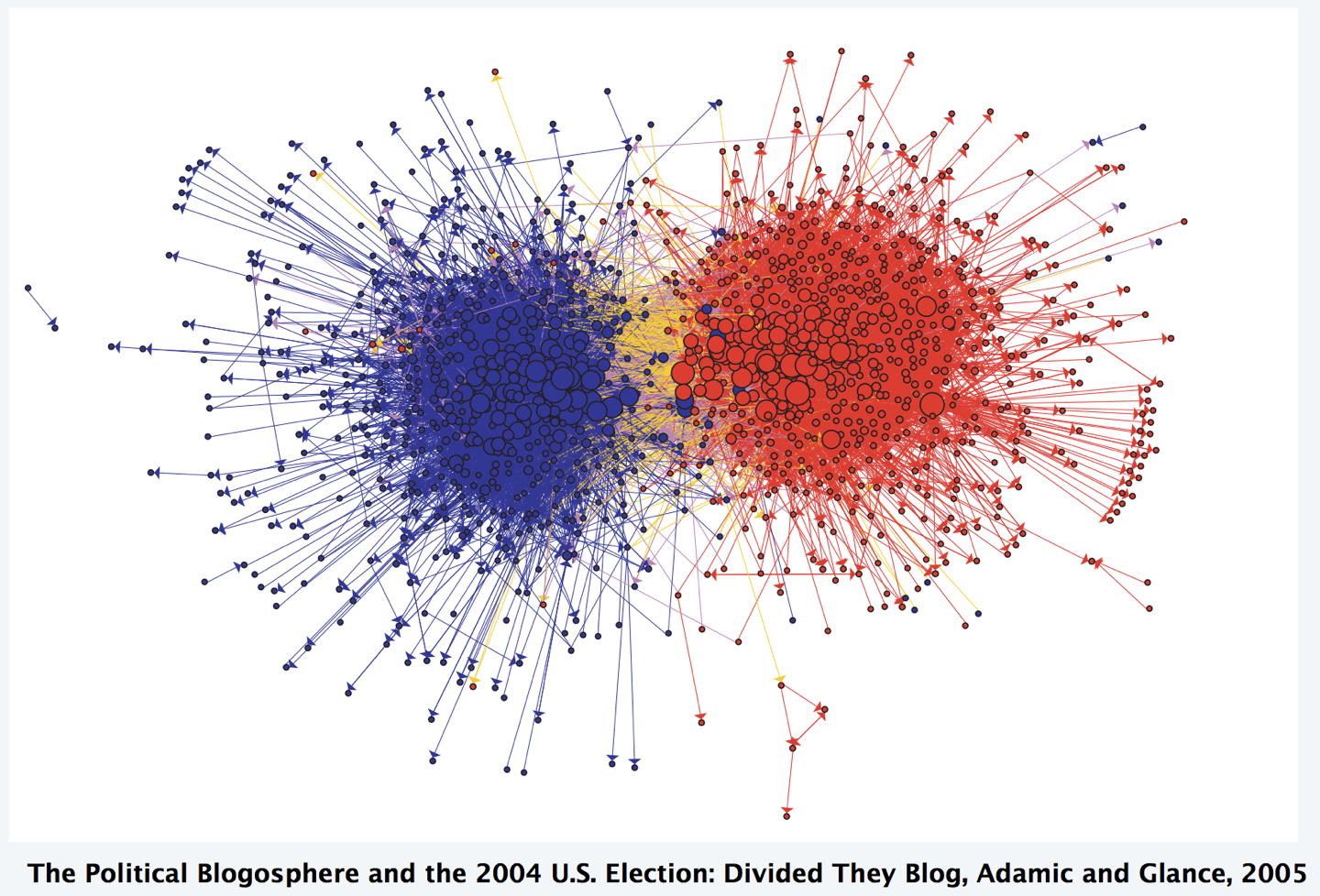
Different types of graphs: partisanship

Slide 14

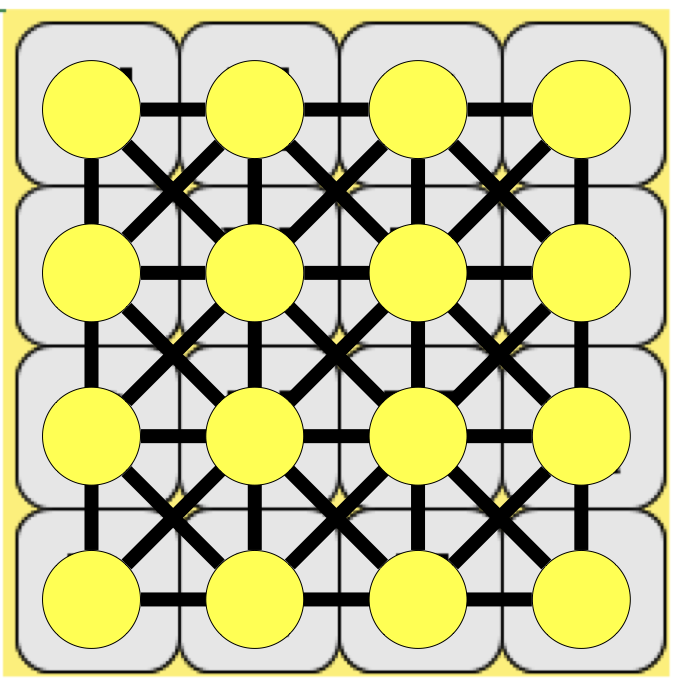
Different types of graphs: Boggle

  • We can represent Boggle as a graph: The Boggle board game The Boggle board game with tiles as nodes and edges to surrounding tiles for each node.

Slide 15

Different types of graphs: Circuit routing

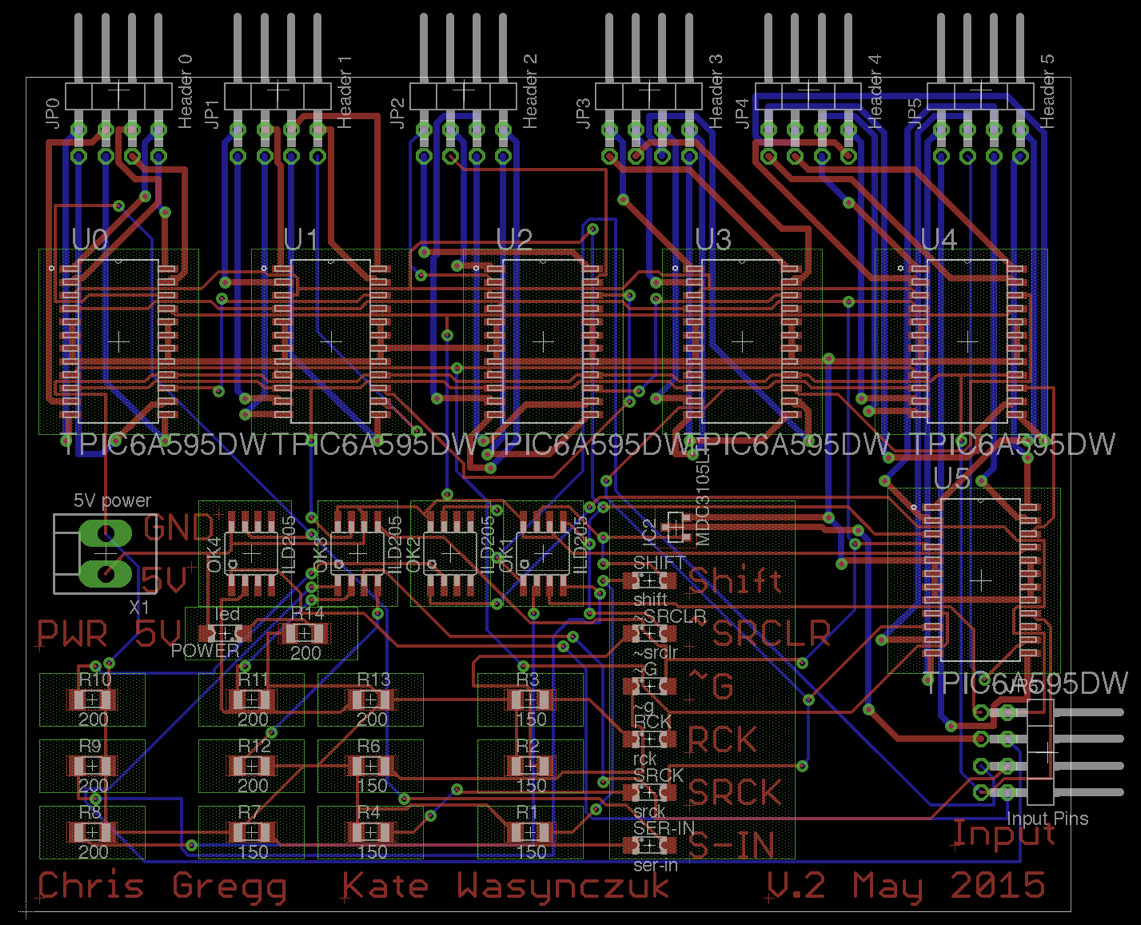
  • When designing circuits, you can have the computer try to "auto route" the circuit, and it uses a graph of all the connections to do so. A circuit PCB layout diagram

Slide 16

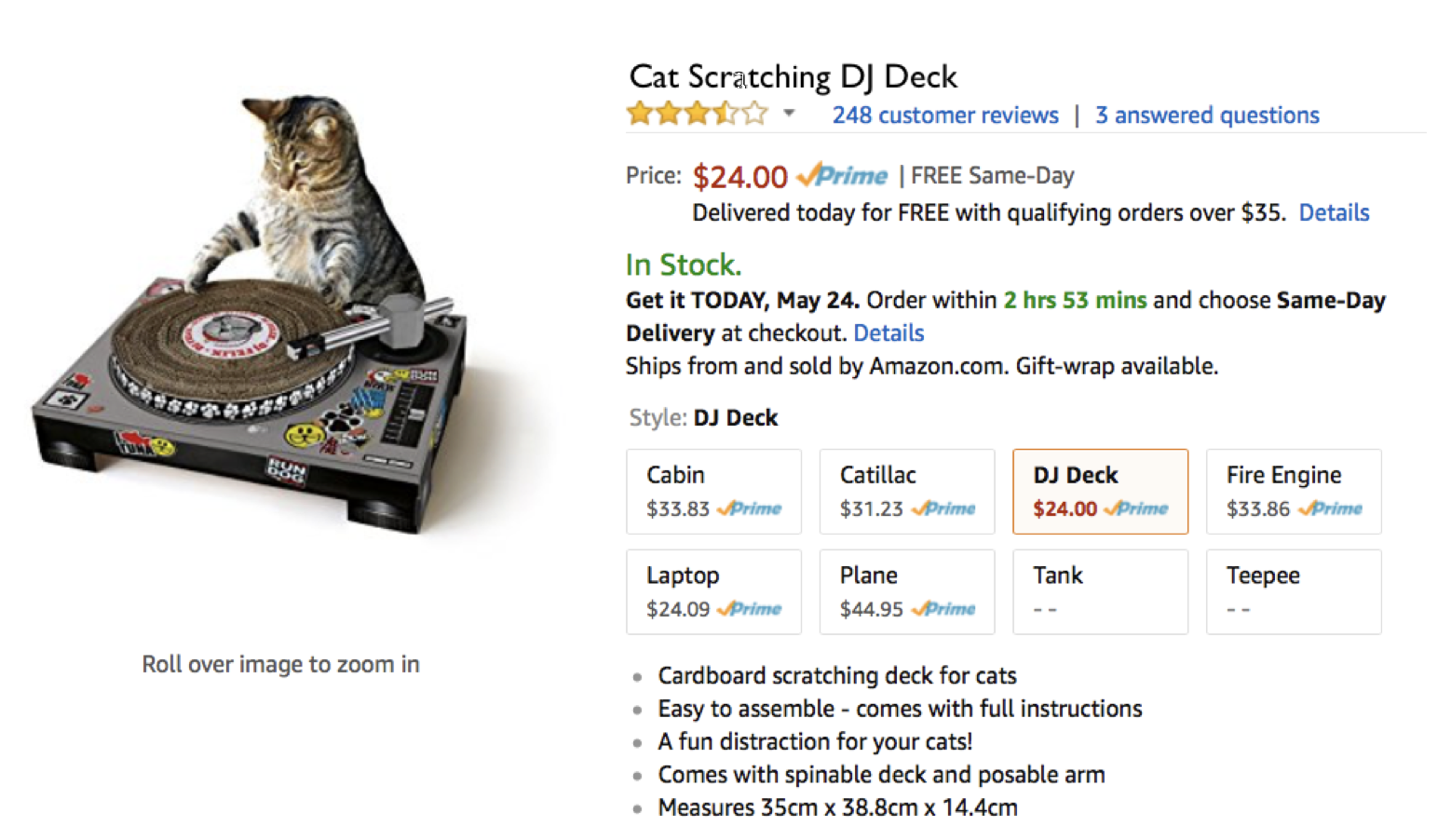
Different types of graphs: Amazon product relationships

  • Amazon.com product relationships are graph-based
  • When you search for an item, you get related items you might want to buy.
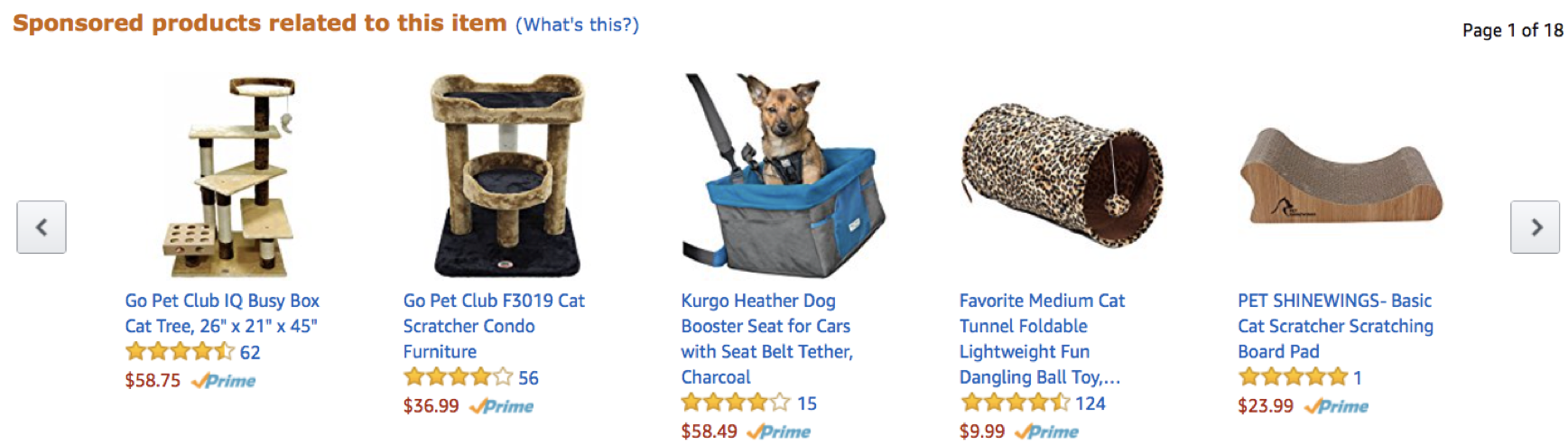
  • For example, what did I search for to get these results? Amazon suggestions: 'cat tree playground for cats', 'scratcher condo for cats', 'dog booster seat`, 'medium cat tunnel', 'basic cat scratcher scratching board pad'
Solution

An image of a cat playing with a 'cat scratching dj deck'

Slide 17

Graph Terms

  • node: the objects in a graph
  • vertex: A vertex is another name for a node.
  • edge: The connections between nodes.
    • directed edge: An edge that only goes in one direction (e.g., from a to b) but not the other way. In a diagram directed edges are arrows.
    • undirected edge: An edge that can go in both directions (e.g., from a to b and from b to a). In a diagram undirected edges are lines.
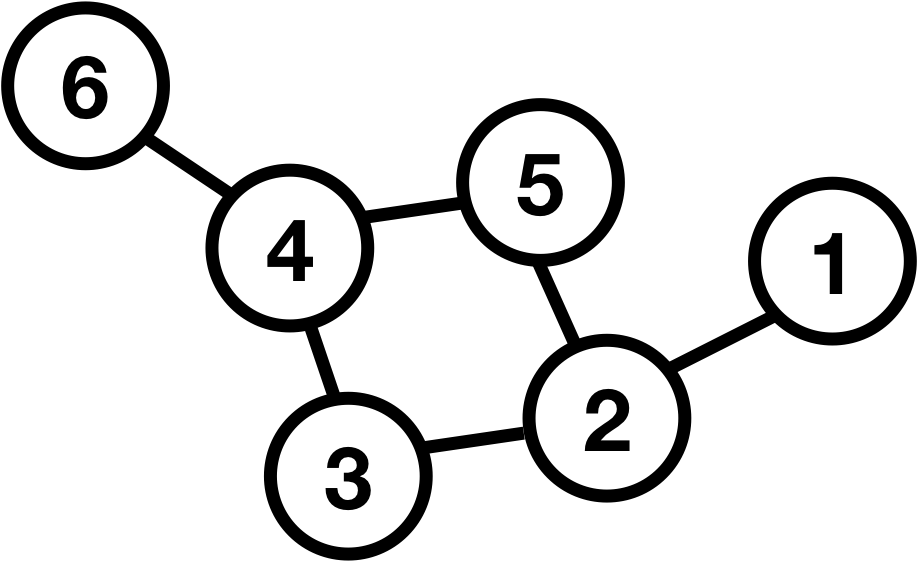
  • path: A path from node a to node b is a sequene of edges that can be followed starting from a to reach b.
    • A path can be represented as nodes visited, or edges taken.
    • In the diagram below, one path from V to Z is {b, h} or `{V, X, Z}'
    • What are two paths from U to Y?
  • path length: The number of nodes or edges contained in a path.
  • neighbor or adjacent: Two nodes connected directly by an edge.
    • Example below: V and X are neighbors.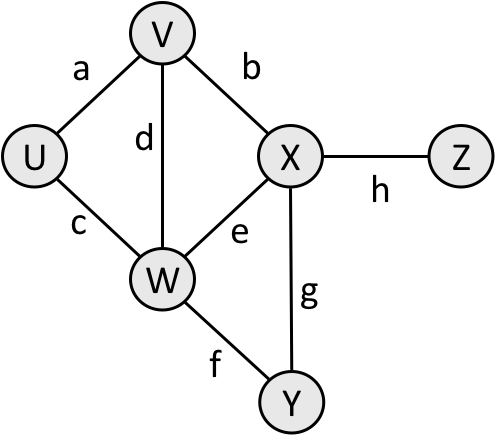 A graph with six nodes. Here are the adjacent nodes: V:UX, U,VW, X:WYZ. UV has edge a, VX has edge b, UW has edge c, VW has edge d, WX has edge e, WY has edge f, XY has edge g, and XZ has edge h
  • A path from U to V and a path from V to Z: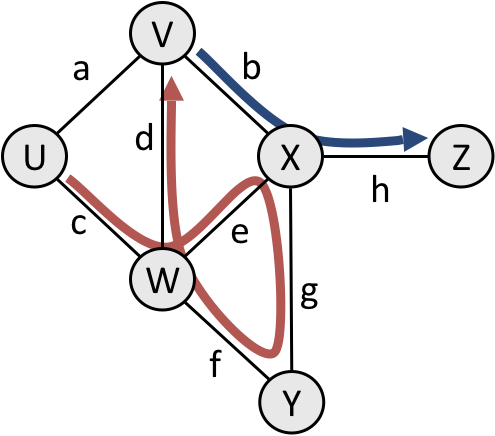 Same as above, except with a path UWXYWV and path VXZ

Slide 18

Loops and cycles

  • cycle: A path that begins and ends at the same node.
    • Examples below:
      • {b, g, f, c, a} or {V, X, Y, W, U, V}
      • {c, d, a} or U, W, V, U
  • acyclic graph: a graph that does not contain any cycles
  • loop: an edge directly from a node to itself
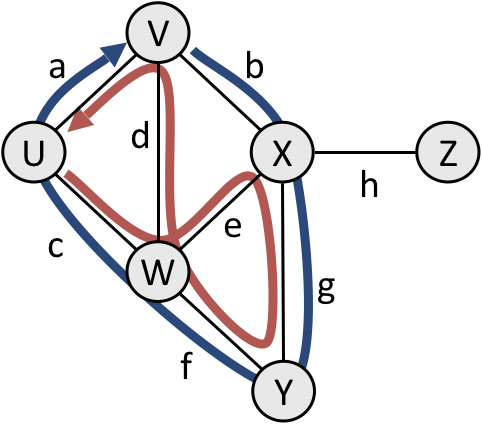
    • Many graphs do not allow loops (you can't be friends with yourself on Facebook) A graph with six nodes. Here are the adjacent nodes: V:UX, U,VW, X:WYZ. UV has edge a, VX has edge b, UW has edge c, VW has edge d, WX has edge e, WY has edge f, XY has edge g, and XZ has edge h Same as above except with a cycle VXYWUV and cycle YWXYWVU

Slide 19

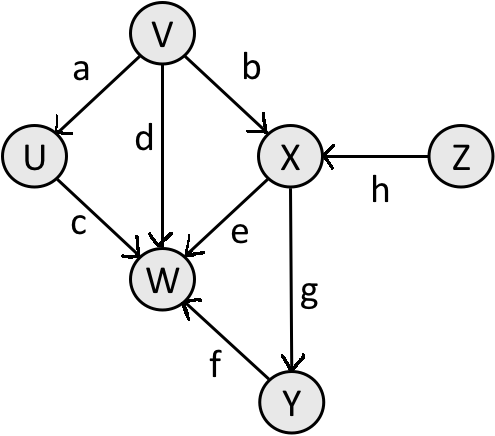
Reachability, connectedness

  • reachable: A node is reachable from another node if a path exists between the two nodes.
  • connected: A graph is connected if every node is reachable from every other node.
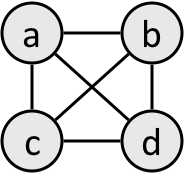
  • complete: A graph is complete if every node has an edge to every other edge (this grows as O(n^2))
  • In the following graph, Z is not reachable from any node. Y is reachable from V, X, Y, and Z, but not U or W. A graph with six nodes. Here are the adjacent nodes: V:UX, U:W, X:WY, Z:W. UV has edge a, VX has edge b, UW has edge c, VW has edge d, WX has edge e, WY has edge f, XY has edge g, and XZ has edge h
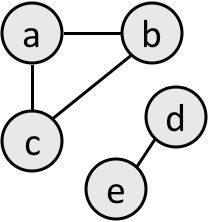
  • A graph that isn't connected: A graph that is not connected. There are five nodes, a, b, c, d, and e. a is connected to b and c, and b is connected to a and c. d and e are connected together. But, there is no connection from a/b/c to d/e
  • A complete graph: A complete graph with nodes a, b, c, and d. Every node has an edge to every other node

Slide 20

Representing Graphs in Code

  • There are a number of different ways to represent graphs.
    • The Stanford library has the BasicGraph class, which allows you to add nodes and edges. E.g, 
      #include "basicgraph.h"
BasicGraph graph;
graph.addNode("a");
graph.addNode("b");
graph.addNode("c");
graph.addNode("d");
graph.addEdge("a", "c");
graph.addEdge("c", "b");
graph.addEdge("b", "d");
graph.addEdge("c", "d");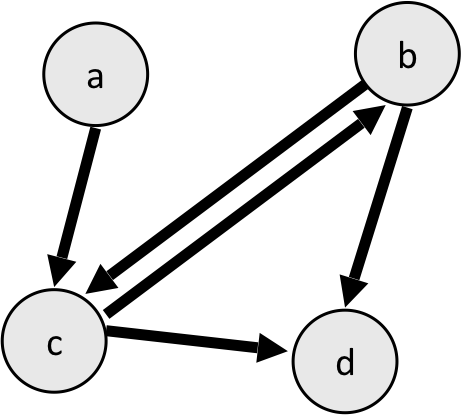

      The basic graph represented by the code above

  • The BasicGraph also has functions for finding a set of all edges, whether two nodes are neighbors, and others.
  • Another way to represent a graph is through an adjacency matrix. An adjacency matrix is a square matrix that represents all edges. For the graph above, the adjacency matrix would be as follows: 
    0 0 1 0
0 0 1 1
0 1 0 1
0 0 0 0
  
Row 0 represents a
Row 1 represents b
Row 2 represents c
Row 3 represents d
The columns represent a, b, c, d
    • a has an edge to c only, so row 0 is 0 0 1 0
    • b has an edge to c and d, so row 1 is 0 0 1 1
    • c has an edge to d only, so row 2 is 0 0 0 1
    • d has no outgoing edges, so row 3 is 0 0 0 0
  • A third way to represent a graph is through an adjacency list. An adjacency list represents each node with a list of its neighbors. There are many different forms of adjancency lists. One might look like this for the graph above: 
    a: c
b: c, d
c: d
d: <none>

Slide 21

Graph Algorithms

  • There are many, many different graph algorithms
  • Some of the famous examples are:
    • Dijkstra's algorithm and the A* algorithm, and Breadth-First-Search
      • These are path-finding algorithms for weighted graphs that are used for finding the shortest path between points. They are significant for applications like Google Maps. Here is a great animation
    • Kruskal's algorithm for finding a minimum spanning tree
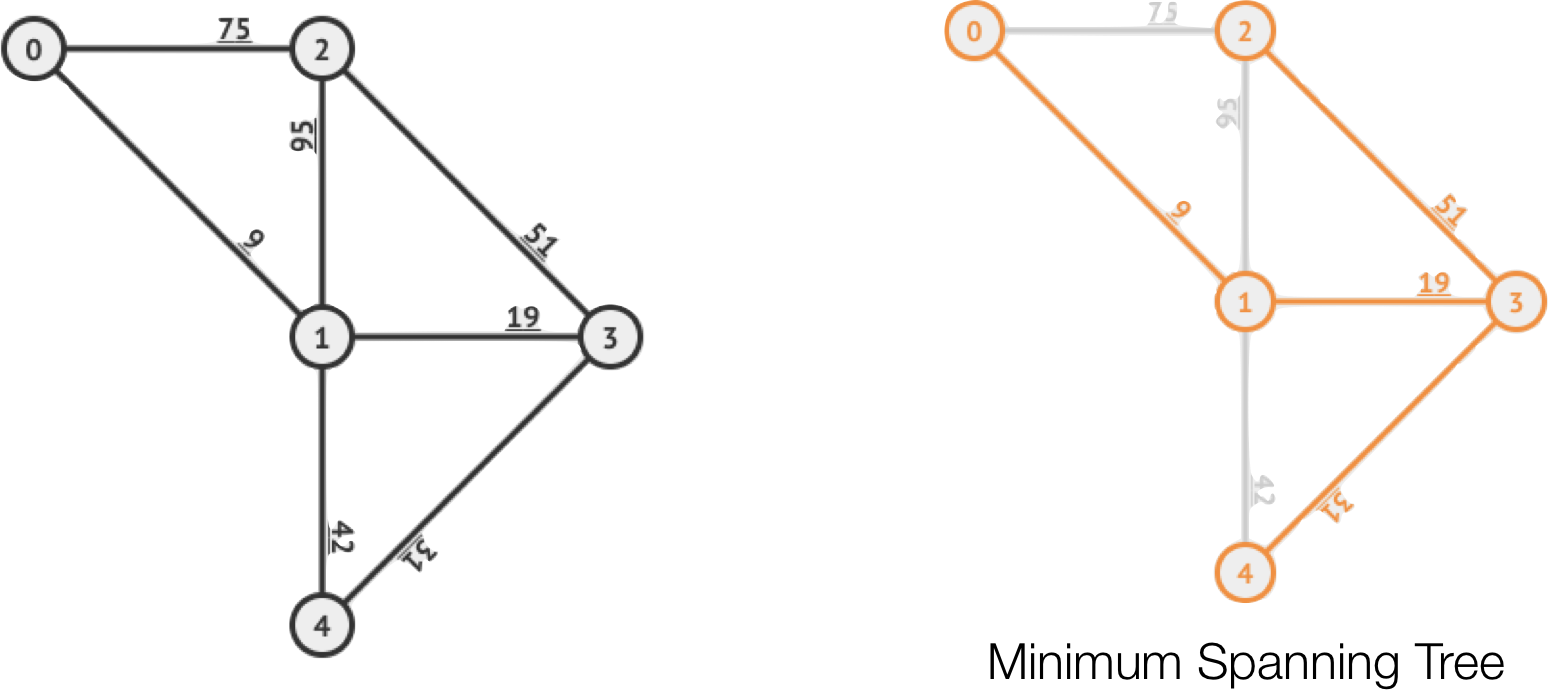
      • This algorithm creates a tree from a graph such that there is the least possible weight between any two nodes. A graph that becomes a minimum spanning tree after applying Kruskal's algorithm
    • Topological Sort
      • A topological sort allows scheduling of work based on dependencies between nodes (e.g., when doing laundry, the washer must finish before the dryer, and before folding). A graph where some nodes depend on others, and following the edges forces the ordering
    • The traveling salesman problem
      • There are many algorithms to solve this problem, but none are efficient. The problem asks, "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?" The cities are modeled as an undirected graph.