Exam instructions: There are 5 questions. Write all answers directly on the exam. This printed exam is closed-book and closed-device; you may refer only to your one letter-sized page of prepared notes and the provided reference sheet. You have 2 hours to complete the exam.
C++ coding guidelines: Unless otherwise restricted in the instructions for a specific problem, you
are free to use any of the CS106 libraries and classes we've covered in class. You don't need #include statements in your
solutions, just assume the required vector, strlib, etc. header files are visible. You do not need
to declare prototypes. You are free to create helper functions unless the problem states otherwise.
Comments are not required, but when your code is incorrect, comments could clarify your
intentions and help earn partial credit.
Q1) C++ Fundamentals
Say we have a Grid of ints, which we'll refer to as grid, that contains 0 in every location except for one, which contains a 1. Such a Grid is shown below. Note the single 1 (which is bold-faced for clarity), which is in the second row, fifth column of the Grid – that would be position grid[1][4].
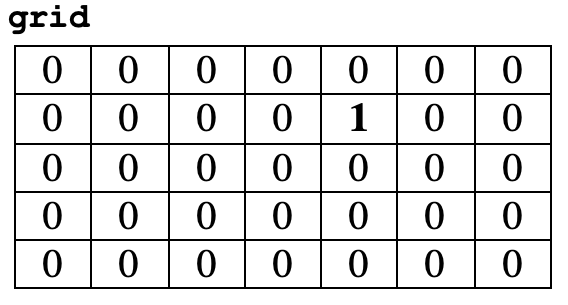
We would like to create a diagonal line of 1's going down and to the right through the Grid, which includes the initial 1 in the Grid and extends to the edges (but does not go outside) of the Grid. So, in the example grid shown above, we would end up with the following final Grid (again, the 1's in the Grid are bold-faced for clarity):
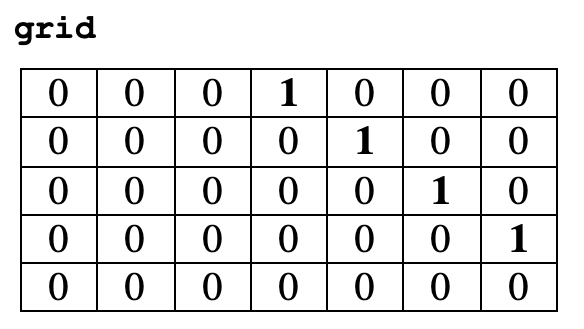
The initial Grid we are given can have any number of rows and columns (but it will be guaranteed to be at least 1x1). You can assume that every element in the Grid you are given, except for one, contains 0's and the remaining element has a 1. Your task in this problem is to write a function:
void diagonalLine(Grid<int>& grid)
which is passed in grid by reference and modifies grid to contain a diagonal line of 1's that includes the 1 initially in the grid. All other elements in the Grid should still be 0's.
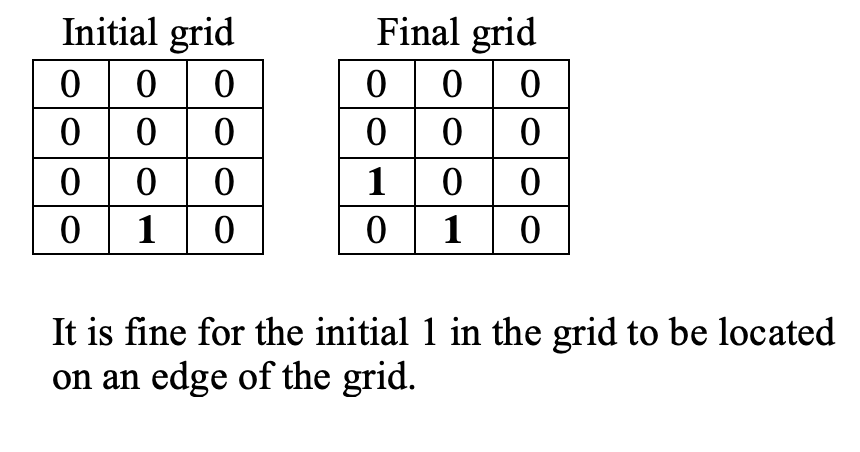
Below, we give two additional examples of initial/final Grids to help further clarify specific cases:

Your code here:
void diagonalLine(Grid<int>& grid)
Q2) ADTS
Google Translate is powered, in large part, by a technique called word2vec that builds an understanding of a language by looking at the context in which each word occurs.
Imagine you have a word like "well." There are certain words that might reasonably appear immediately before the word "well" in a sentence, like "feeling," "going," "reads," etc., and some words that that are highly unlikely to appear before "well," like "cake," "circumspection," and "election." The idea behind word2vec is to find connections between words by looking for pairs of words that have similar sets of words preceding them. Those words likely have some kind of connection between them, and the rest of the logic in word2vec works by trying to discover what those connections are.
Your task is to write a function:
Map<string, Set<string>> predecessorMap(Vector<string>& input)
that takes as input a Vector of strings representing the lines of a file, and returns a Map<string, Set<string>> that associates each word in the file with all the words that appeared directly before that word. For example, given a Vector containing the lines of JFK’s famous quote:
Ask not what your country can do for you;
ask what you can do for your country,
would look like:
{"Ask not what your country can do for you;", "ask what you can do for your country,"}
and function should return a Map with these key/value pairs:
"not" : { "ask" }
"what" : { "not", "ask" }
"your" : { "what", "for" }
"country" : { "your" }
"can" : { "country", "you" }
"do" : { "can" }
"for" : { "do" }
"you" : { "for", "what" }
"ask" : { "you" }
Notice that although the word "ask" appears twice in the quote, the first time it appears it’s the first word in the file and so nothing precedes it. The second time it appears, it’s preceded by a word from a different line, "you," which is what ultimately appears in the output map.
Some notes on this problem:
- You can assume you have access to a function
Vector<string> tokenize(string line)
that takes in a line, accurately tokenizes it into cleaned words (stripped of all punctuation, but with the original casing retained), and returns all of the words in the line as a Vector of strings. - If a word in a line contains no letters, it gets stripped to the empty string by the aformentioned
tokenizefunction:
tokenize("hi there 123")returns{"hi", "there", ""}
and your map-building process should completely ignore these empty tokens. - Your code should be case-insensitive, so it should return the same result regardless of the capitalization of the words in the file. The capitalization of the keys in the map is completely up to you.
- You have no guarantees about the number of strings in the Vector or the number of words in each string within the Vector.
Your code here:
Map<string, Set<string>> predecessorMap(Vector<string>& input)
Q3) Code study: ADTs and Big-O
This question is designed to let you demonstrate what you’ve learned about algorithmic analysis and data structure design. Below are four functions. We picked one of those functions and ran it on many different values of n. We captured the output of that function on each of those inputs, along with the runtime. That information is printed in the table below.
Function 1
int function1(int n) {
Stack<int> values;
for (int i = 0; i < n; i++) {
values.push(i);
}
int result;
while (!values.isEmpty()) {
result = values.pop();
}
return result;
}
Function 2
int function2(int n) {
Queue<int> values;
for (int i = 0; i < n; i++) {
values.enqueue(i);
}
int result;
while (!values.isEmpty()) {
result = values.dequeue();
}
return result;
}
Function 3
int function3(int n) {
Set<int> values;
for (int i = 0; i < n; i++) {
values.add(i);
}
int result;
for (int value: values) {
result = value;
}
return result;
}
Function 4
int function4(int n) {
Vector<int> values;
for (int i = 0; i < n; i++) {
values.add(i);
}
int result;
while (!values.isEmpty()) {
result = values[0];
values.remove(0);
}
return result;
}
| n | Time | Return value |
|---|---|---|
| 100,000 | 0.137s | 99999 |
| 200,000 | 0.274s | 199999 |
| 300,000 | 0.511s | 299999 |
| 400,000 | 0.549s | 399999 |
| 500,000 | 0.786s | 499999 |
| 600,000 | 0.923s | 599999 |
| 700,000 | 0.960s | 699999 |
| 800,000 | 1.198s | 799999 |
| 900,000 | 1.335s | 899999 |
| 1,000,000 | 1.472s | 999999 |
a) For each of these pieces of code, tell us its big-O runtime as a function of n. No justification is required.
Your answer here:
b) For each of these pieces of code, tell us whether that function could have given rise to the return values reported in the rightmost column of the table below. No justification is required.
Your answer here:
c) Which piece of code did we run to produce the table above? How do you know? Justify your answer.
Your answer here:
Q4) Tracing Recursion
a) For each of the calls to the recursive function below, indicate what output is produced:
void recursionTrace(int n) {
if (n <= 1) {
cout << ": ";
} else {
cout << (n % 2) << " ";
recursionTrace(n / 2);
cout << n << " ";
}
}
Write your answer below:
Call Printed value
----------------------------------------------------
recursionTrace(8) Your answer here:
recursionTrace(25) Your answer here:
recursionTrace(46) Your answer here:
b) For each of the calls to the recursive function below, indicate what output is produced:
int sillyFunc(int a, int b) {
if (b == 0) {
return 1;
} else {
return a * sillyFunc(a, b - 1);
}
}
Write your answer below:
Call Printed value
----------------------------------------------------
sillyFunc(10, 0) Your answer here:
sillyFunc(5, 2) Your answer here:
sillyFunc(4, 3) Your answer here:
c) What mathematical function does sillyFunc calculate?
Your answer here:
Q5) Recursive Function
Chapter exercise 7.7 from the textbook
Write a recursive function:
int digitSum(int n)
that takes a non-negative integer and returns the sum of its digits. For example, calling digitSum(1729) returns 19, since this is 1 + 7 + 2 + 9.
The recursive implementation of digitSum depends on the fact that it is very easy to break an integer down into two components using division by 10. For example, given the integer 1729, you can divide it into two pieces as follows:
1729
/ \
172 9
Each of the resulting integers is strictly smaller than the original and thus represents a simpler case.
1729
/ \
172 9
/ \ \
17 2 9
/ \ \ \
1 7 2 9
Your code here:
int digitSum(int n)