\(K\)-nearest neighbors#

Fig 3.16

Fig. 15 Illustration of KNN regression: \(K=1\) (left) is rougher than \(K=9\) (right)#

KNN estimator#

\[\hat f(x) = \frac{1}{K} \sum_{i\in N_K(x)} y_i\]

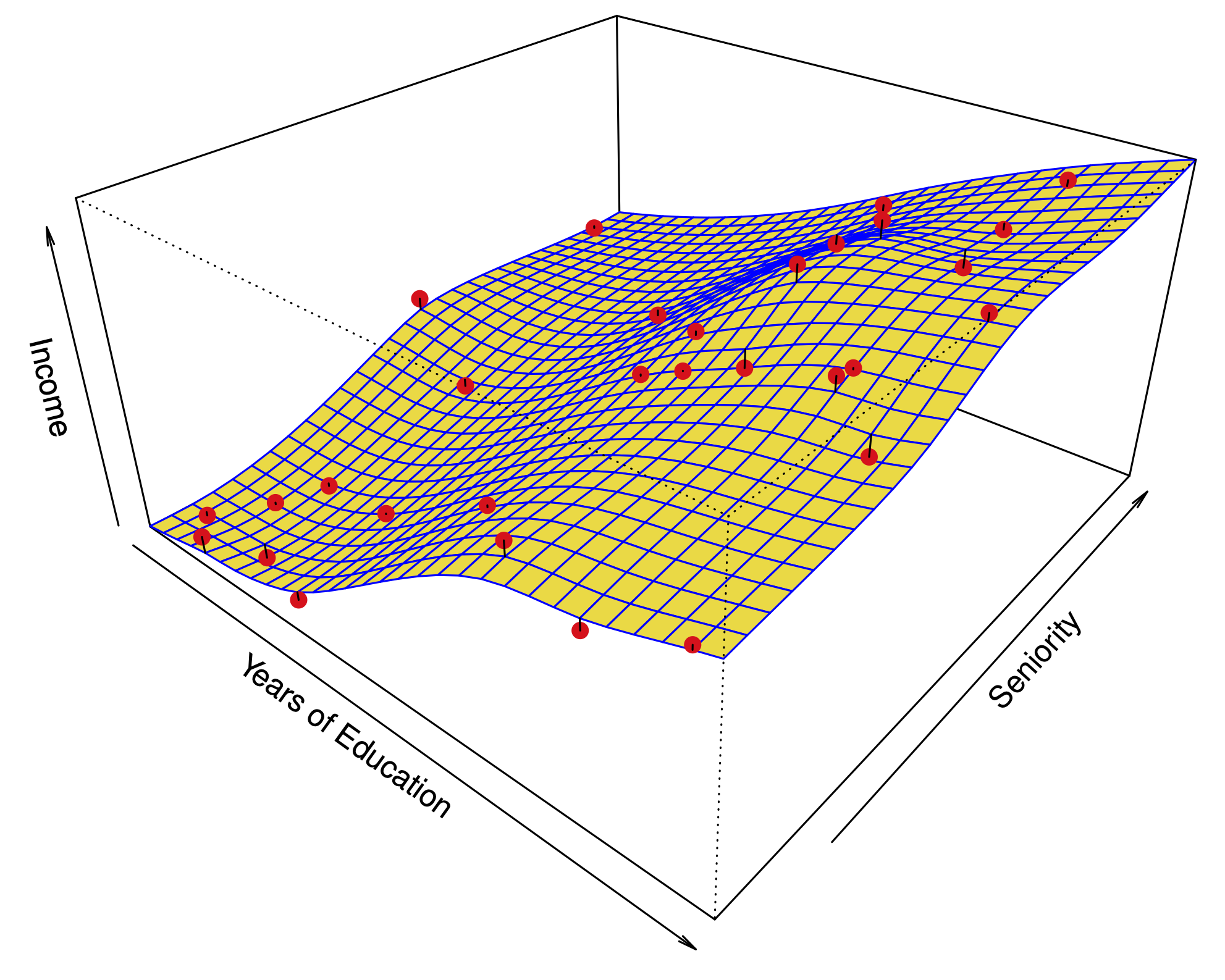
Comparing linear regression to \(K\)-nearest neighbors#

  • Linear regression: prototypical parametric method. Easy for inference.

  • KNN regression: prototypical nonparametric method. Inference less clear.

Long story short:#

  • KNN is only better when the function \(f\) is far from linear (in which case linear model is misspecified)

  • When \(n\) is not much larger than \(p\), even if \(f\) is nonlinear, Linear Regression can outperform KNN.

  • KNN has smaller bias, but this comes at a price of higher variance.

KNN estimates for a simulation from a linear model#

Fig 3.17

  • \(K=1\) on left, \(K=9\) on right.

Linear models can dominate KNN#

Fig 3.18

  • Truth is linear, plot of test MSE vs. 1/K shows KNN worse than linear regression.

Increasing deviations from linearity#

Fig 3.19

When there are more predictors than observations, Linear Regression dominates#

Fig 3.20

  • When \(p\gg n\), each sample has no near neighbors, this is known as the curse of dimensionality.

  • The variance of KNN regression is very large.