Contents

Poisson data (4.3)

  • Suppose \(Y \sim \text{Poisson}(\lambda)\).

  • Then, for \(y=0,1,2, \dots\)

\[\begin{split} \begin{aligned} P_{\lambda}(Y=y) &= \frac{\lambda^y}{y!} e^{-\lambda} \\ &= \exp(y \cdot \log \lambda) \frac{e^{-\lambda}}{y!} \end{aligned} \end{split}\]

  • This is one-parameter exponential family with sufficient statistic \(y\), natural parameter \(\log \lambda\), \(b(y)=1/y!\) and \(m\) counting measure on \(\{0,1,2,\dots\}\).

Generalized linear models for counts

  • Poisson is a natural model for counts (arguably, we might say this is because it appears in many limiting arguments involving counts).

  • Given \((Y_i,X_i)\) with \(Y_i \sim Poisson(\lambda_i)\), the log-linear model is

\[ \log\left(\lambda_i\right) = X_i^T\beta \]

with

\[ \lambda_i = E[Y_i|X_i]. \]

  • Just as there is a canonical link for Binomial data, there is one for Poisson as well. (What is canonical link for Gaussian?)

  • The log link here is related to conditional independencies among features \(X\) and response \(Y\).

  • Note that for Poisson data $\( \text{Var}[Y_i|X_i] = \lambda_i. \)$

Interpretation of coefficients

\[\frac{E_{\beta}(Y|\dots, X_j=x_j+1, \dots)}{E_{\beta}(Y|\dots, X_j=x_j, \dots)} = e^{\beta_j}\]

Likelihood for log-linear models

  • The Poisson deviance for the log-linear model is $\( DEV(\beta|Y) = 2 \sum_{i=1}^n \left[\exp(X_i^T\beta) - Y_i(X_i^T\beta) - Y_i + Y_i \log(Y_i) \right] \)$

  • Derivatives

\[\begin{split} \begin{aligned} \nabla DEV(\beta|Y) &= 2 X^T(\exp(X\beta) - Y ) \\ &= 2 X^T(E_{\beta}(Y) - Y) \\ \nabla^2 DEV(\beta|Y) &= 2 X^T\exp(X\beta)X \\ &= 2 X^T \text{Var}_{\beta}(Y)X \end{aligned} \end{split}\]

  • Similar form to logistic regression.

library(glmbb) # for `crabs` data
data(crabs)
satell_log = glm(satell ~ width + color, family=poisson(), data=crabs)
summary(satell_log)

Call:
glm(formula = satell ~ width + color, family = poisson(), data = crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.0415  -1.9581  -0.5575   0.9830   4.7523  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.08640    0.55750  -5.536 3.09e-08 ***
width        0.14934    0.02084   7.166 7.73e-13 ***
colordarker -0.01100    0.18041  -0.061   0.9514    
colorlight   0.43636    0.17636   2.474   0.0133 *  
colormedium  0.23668    0.11815   2.003   0.0452 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 559.34  on 168  degrees of freedom
AIC: 924.64

Number of Fisher Scoring iterations: 6

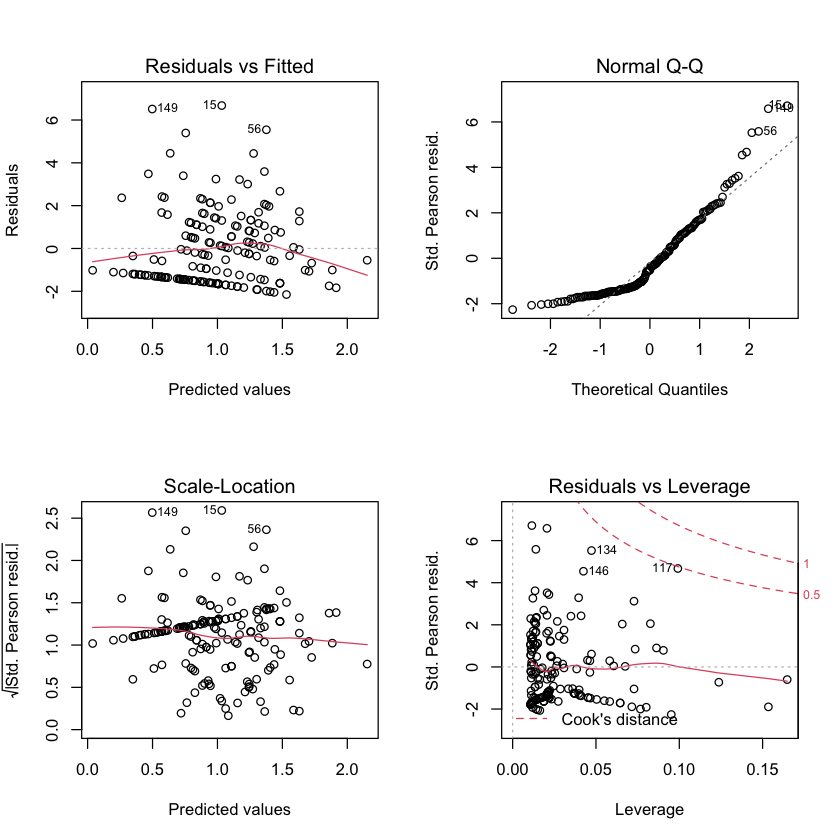
par(mfrow=c(2,2))
plot(satell_log)
../_images/GLM_II_5_0.png

Newton-Raphson for log-linear models

  • After initialization $\( \hat{\beta}^{(k+1)} = \hat{\beta}^{(k)} + (X^T\exp(X\hat\beta^{(k)})X)^{-1} X^T(Y - \exp(X\hat\beta^{(k)})) \)$

  • Can be written as IRLS with weights and response

\[\begin{split} \begin{aligned} W^{(k+1)} &= \exp(X\hat\beta^{(k)}) \\ Z^{(k+1)} &= X\hat{\beta}^{(k)} + (Y - \exp(X\hat\beta^{(k)}))/ \exp(X\hat\beta^{(k)}) \\ &= g(E_{\hat{\beta}^{(k)}}(Y)) + g'(E_{\hat{\beta}^{(k)}}(Y)) \cdot (Y - E_{\hat{\beta}^{(k)}}(Y)) \\ &= g(\hat{\mu}^{(k)}) + g'(\hat{\mu}^{(k)})(Y - \hat{\mu}^{(k)}) \end{aligned} \end{split}\]

“Unnatural models”

  • We could use a different link function

\[ g(\lambda_i) = X_i^T\beta \]

or,

\[ \lambda_i = g^{-1}(X_i^T\beta) \]

  • Deviance is now

\[ DEV(\beta|Y) = 2 \sum_{i=1}^n \left[g^{-1}(X_i^T\beta) - Y_i \log(g^{-1}(X_i^T\beta)) - Y_i + Y_i \log(Y_i) \right] \]

  • Usual choices in software for Poisson is log (canonical: default). Others:

    • identity: \(g(x)=x\)

    • inverse: \(g(x)=1/x\).

satell_inverse = glm(satell ~ width + color, 
                     family=poisson(link='inverse'), 
                     data=crabs)
summary(satell_inverse)

Call:
glm(formula = satell ~ width + color, family = poisson(link = "inverse"), 
    data = crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.8701  -2.0606  -0.4481   1.0042   4.6942  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  1.259804   0.136929   9.200  < 2e-16 ***
width       -0.031806   0.004905  -6.484 8.92e-11 ***
colordarker  0.011778   0.077006   0.153   0.8784    
colorlight  -0.126441   0.055752  -2.268   0.0233 *  
colormedium -0.085615   0.045740  -1.872   0.0612 .  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 574.53  on 168  degrees of freedom
AIC: 939.82

Number of Fisher Scoring iterations: 8

“Unnatural models”

  • Derivatives

\[\begin{split} \begin{aligned} \nabla DEV(\beta|Y) &= 2 X^T\left(\frac{1 - \frac{Y}{g^{-1}(X\beta)}}{g'(g^{-1}(X\beta))}\right) \\ &= 2 X^T\left(\frac{1 - \frac{Y}{E_{\beta}(Y)}}{g'(E_{\beta}(Y))}\right) \\ E_{\beta}\left[\nabla^2 DEV(\beta|Y) \right] &= 2 X^T\left(\frac{1}{g'(E_{\beta}(Y))^2 E_{\beta}(Y)}\right)X \\ &= 2 X^TW_{\beta}X \end{aligned} \end{split}\]

with

\[ W_{\beta} = \text{diag}(1 / (\lambda_i g'(\lambda_i)^2)), \qquad \lambda_i = g^{-1}(X_i^T\beta) \]

“Unnatural models”

  • Fisher scoring $\( \hat{\beta}^{(k+1)} = \hat{\beta}^{(k)} + (X^TW_{\hat{\beta}^{(k)}}X)^{-1}X^T\left(\frac{1 - \frac{Y}{E_{\beta}(Y)}}{g'(E_{\beta}(Y))}\right) \)$

  • Equivalent to IRLS with

\[\begin{split} \begin{aligned} W^{(k+1)} &= W_{\hat{\beta}^{(k)}} \\ Z^{(k+1)} &= \hat{\eta}^{(k)} + g'(\hat{\mu}^{(k)})(Y - E_{\hat{\beta}^{(k)}}(Y)) \end{aligned} \end{split}\]

with

\[ \hat{\eta}^{(k)} = X\hat{\beta}^{(k)} = g(\hat{\mu}^{(k)}). \]

  • Form of weights comes from “\(\text{Var}(Z)\)”.

  • Recall that \(E_{\beta}(Y)=\text{Var}_{\beta}(Y)\) for Poisson data.

Distribution of \(\hat{\beta}\)

  • Using our usual Taylor series $\( \hat{\beta} - \beta^* \approx N\left(0, (X^TW^{(\infty)}X)^{-1} \text{Var}(X^TW^{(\infty)}Z^{(\infty)})(X^TW^{(\infty)}X)^{-1} \right) \)$

  • When model is correct, $\( \text{Var}(X^TW^{(\infty)}Z^{(\infty)}) \approx X^TW^{(\infty)}X \)\( so asymptotic distribution is \)\( \hat{\beta} - \beta^* \approx N\left(0, (X^TW^{(\infty)}X)^{-1} \right). \)$

  • This is covariance that R reports to us with vcov.

X = model.matrix(satell_log)
W = fitted(satell_log)
solve(t(X) %*% (W * X))
A matrix: 5 × 5 of type dbl
(Intercept)widthcolordarkercolorlightcolormedium
(Intercept) 0.310805970-0.0114263483-0.0162473663 0.0019301044 0.0027713727
width-0.011426348 0.0004343334 0.0002297147-0.0004612394-0.0004932173
colordarker-0.016247366 0.0002297147 0.0325477977 0.0099601366 0.0099432238
colorlight 0.001930104-0.0004612394 0.0099601366 0.0311020571 0.0107278527
colormedium 0.002771373-0.0004932173 0.0099432238 0.0107278527 0.0139590542
 
vcov(satell_log)
A matrix: 5 × 5 of type dbl
(Intercept)widthcolordarkercolorlightcolormedium
(Intercept) 0.310805898-0.0114263456-0.0162473648 0.0019301016 0.0027713695
width-0.011426346 0.0004343333 0.0002297147-0.0004612393-0.0004932172
colordarker-0.016247365 0.0002297147 0.0325477151 0.0099601366 0.0099432238
colorlight 0.001930102-0.0004612393 0.0099601366 0.0311020569 0.0107278525
colormedium 0.002771369-0.0004932172 0.0099432238 0.0107278525 0.0139590539
 
X = model.matrix(satell_inverse)
W = fitted(satell_inverse)^3
solve(t(X) %*% (W * X))
A matrix: 5 × 5 of type dbl
(Intercept)widthcolordarkercolorlightcolormedium
(Intercept) 0.0187471088-6.400857e-04-2.108431e-03-7.723414e-04-1.139935e-04
width-0.0006400857 2.405665e-05 1.474627e-05-3.546863e-05-6.021163e-05
colordarker-0.0021084309 1.474627e-05 5.933203e-03 1.694329e-03 1.679162e-03
colorlight-0.0007723414-3.546863e-05 1.694329e-03 3.108126e-03 1.804845e-03
colormedium-0.0001139935-6.021163e-05 1.679162e-03 1.804845e-03 2.092418e-03
 
vcov(satell_inverse)
A matrix: 5 × 5 of type dbl
(Intercept)widthcolordarkercolorlightcolormedium
(Intercept) 0.0187494465-6.401830e-04-0.0021081258-0.0007720202-1.136107e-04
width-0.0006401830 2.406026e-05 0.0000147454-0.0000354700-6.021527e-05
colordarker-0.0021081258 1.474540e-05 0.0059298789 0.0016940499 1.678885e-03
colorlight-0.0007720202-3.547000e-05 0.0016940499 0.0031082448 1.804558e-03
colormedium-0.0001136107-6.021527e-05 0.0016788847 0.0018045581 2.092165e-03

Distribution of \(\hat{\beta}\)

  • When model is incorrectly specified, the parameter we are estimating (under \((X_i,Y_i) \overset{IID}{\sim} F\)) is a solution to $\( 0 = E_F\left [X \cdot \frac{1 - \frac{Y}{g^{-1}(X\beta^*(F))}}{g'(g^{-1}(X\beta^*(F)))} \right] \)$

  • Must use some method (sandwich, bootstrap) to estimate covariance of the above random vector (multiplied by \((X^TWX)^{-1}\)).

Overdispersion

  • Poisson model says $\( \text{Var}(Y_i) = E(Y_i). \)$

  • This may not be true (or close to true).

  • Simple clustering models yield plausible model $\( \text{Var}(Y_i) = \phi \cdot E(Y_i). \)$

library(dplyr)
crabs$groups = cut(crabs$width, breaks=c(0, seq(23.25, 29.25, by=1), max(crabs$width)))
results = crabs %>%
          group_by(groups) %>%
          summarize(N=n(), numS = mean(satell), varS = var(satell))

Attaching package: ‘dplyr’

The following objects are masked from ‘package:stats’:

    filter, lag

The following objects are masked from ‘package:base’:

    intersect, setdiff, setequal, union

`summarise()` ungrouping output (override with `.groups` argument)

results
A tibble: 8 × 4
groupsNnumSvarS
<fct><int><dbl><dbl>
(0,23.2] 141.000000 2.769231
(23.2,24.2]141.428571 8.879121
(24.2,25.2]282.392857 6.543651
(25.2,26.2]392.69230811.376518
(26.2,27.2]222.863636 6.885281
(27.2,28.2]243.875000 8.809783
(28.2,29.2]183.94444416.879085
(29.2,33.5]145.142857 8.285714

Quasilikelihood

  • Begins with observation that fitting a GLM with variance function

\[ V_{Q}(\mu) = \phi \cdot V(\mu) \]

yields exactly the same fitted value whatever \(\phi\) we use.

  • (Similar to observation that OLS estimators in Gaussian regression are MLE even when \(\sigma^2\) unknown, whatever \(\sigma^2\) is.)

  • A rearrangement of \(\nabla \text{DEV}\) yields the form $\( 2 X^TV(\hat{\mu}^{(k)})^{-1}(\hat{\mu}^{(k)} - Y) \frac{d\mu}{d\eta}\biggl|_{\eta=X\hat{\beta}^{(k)}} \)$

  • IRLS algorithm will find a zero of “gradient” above for any pair \((g,V)\)

Quasilikelihood

Estimate of dispersion

\[ \hat{\phi} = \frac{1}{n-p} \sum_{i=1}^n \frac{(Y_i - \hat{\mu}_i)^2 }{V(\hat{\mu}_i)} = \frac{1}{n-p} X^2(M) \]

  • R reports (?) asymptotic distribution

\[ \hat{\beta}-\beta^* \approx N(0, \hat{\phi} \cdot (X^TW^{(\infty)}X)^{-1}) \]

  • Tough to justify covariance as there is no likelihood behind our model.

  • A sandwich / bootstrap estimator may give a better estimate of the variance.

summary(glm(satell ~ width + color, family=quasipoisson(), data=crabs))
c(0.037 / 0.020, sqrt(3.23))

Call:
glm(formula = satell ~ width + color, family = quasipoisson(), 
    data = crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.0415  -1.9581  -0.5575   0.9830   4.7523  

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -3.08640    1.00251  -3.079  0.00243 ** 
width        0.14934    0.03748   3.985  0.00010 ***
colordarker -0.01100    0.32442  -0.034  0.97300    
colorlight   0.43636    0.31713   1.376  0.17066    
colormedium  0.23668    0.21246   1.114  0.26687    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for quasipoisson family taken to be 3.233628)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 559.34  on 168  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 6
  1. 1.85
  2. 1.79722007556114
summary(satell_log, dispersion=3.228764)

Call:
glm(formula = satell ~ width + color, family = poisson(), data = crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.0415  -1.9581  -0.5575   0.9830   4.7523  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.08640    1.00176  -3.081  0.00206 ** 
width        0.14934    0.03745   3.988 6.66e-05 ***
colordarker -0.01100    0.32417  -0.034  0.97294    
colorlight   0.43636    0.31689   1.377  0.16851    
colormedium  0.23668    0.21230   1.115  0.26492    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 3.228764)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 559.34  on 168  degrees of freedom
AIC: 924.64

Number of Fisher Scoring iterations: 6

summary(satell_log)

Call:
glm(formula = satell ~ width + color, family = poisson(), data = crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.0415  -1.9581  -0.5575   0.9830   4.7523  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.08640    0.55750  -5.536 3.09e-08 ***
width        0.14934    0.02084   7.166 7.73e-13 ***
colordarker -0.01100    0.18041  -0.061   0.9514    
colorlight   0.43636    0.17636   2.474   0.0133 *  
colormedium  0.23668    0.11815   2.003   0.0452 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 559.34  on 168  degrees of freedom
AIC: 924.64

Number of Fisher Scoring iterations: 6

Negative binomial (4.3.4)

  • One model sometimes used instead of Poisson is

\[ Y \sim \text{Negative binomial}(\mu,k) \]

where

\[ P(Y=y) = \frac{\Gamma(y+k)}{\Gamma(k) \Gamma(y+1)} \left(\frac{k}{\mu+k} \right)^k \left(1 - \frac{k}{\mu+k} \right)^y, \qquad y=0,1,2,\dots \]

  • Note: this is not the usual parametrization of the negative binomial.

Negative binomial

  • In this model

\[\begin{split} \begin{aligned} E[Y] &= \mu \\ \text{Var}(Y) &= \mu + \mu^2 / k \end{aligned} \end{split}\]

so that it is a GLM for \(k\) fixed.

  • In practice, we don’t know \(k\)…

library(MASS)
satell_nb = MASS::glm.nb(satell ~ width + color, data=crabs)
summary(satell_nb)

Attaching package: ‘MASS’

The following object is masked _by_ ‘.GlobalEnv’:

    crabs

The following object is masked from ‘package:dplyr’:

    select

Call:
MASS::glm.nb(formula = satell ~ width + color, data = crabs, 
    init.theta = 0.9320986132, link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.8714  -1.3769  -0.2663   0.4410   2.2496  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.87271    1.19047  -3.253  0.00114 ** 
width        0.17839    0.04529   3.939 8.18e-05 ***
colordarker -0.01570    0.33125  -0.047  0.96220    
colorlight   0.52033    0.38396   1.355  0.17536    
colormedium  0.24440    0.22864   1.069  0.28510    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for Negative Binomial(0.9321) family taken to be 1)

    Null deviance: 216.56  on 172  degrees of freedom
Residual deviance: 196.23  on 168  degrees of freedom
AIC: 760.6

Number of Fisher Scoring iterations: 1


              Theta:  0.932 
          Std. Err.:  0.168 

 2 x log-likelihood:  -748.596 

# Standard errors have changed, estimates are similar
summary(satell_log)

Call:
glm(formula = satell ~ width + color, family = poisson(), data = crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.0415  -1.9581  -0.5575   0.9830   4.7523  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.08640    0.55750  -5.536 3.09e-08 ***
width        0.14934    0.02084   7.166 7.73e-13 ***
colordarker -0.01100    0.18041  -0.061   0.9514    
colorlight   0.43636    0.17636   2.474   0.0133 *  
colormedium  0.23668    0.11815   2.003   0.0452 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 559.34  on 168  degrees of freedom
AIC: 924.64

Number of Fisher Scoring iterations: 6

previous

Generalized linear models (Ch. 4)

next

Bayesian methods for GLMs (7.2)