Section #2: Variables & Control Flow
September 27th, 2020
Written by Brahm Capoor, Juliette Woodrow, Parth Sarin, Kara Eng & Tori Qiu
This week in section, your goal is to practice and gain familiarity with the principles of variables and control flow.
Tracing
The following is code for an interactive console program that performs
a type of calculation that is probably familiar. Examing the code.
What is the role of the SENTINEL constant? How do each of
the four variables-a, b, x and
y-change over time? Overall, what common task does this
program do?
"""
File: mystery_calculation.py
----------------------------
It's your job to figure out what this program does!
"""
SENTINEL = -1
def main():
a = int(input("Enter a value for a: "))
b = int(input("Enter a value for b: "))
x = int(input("Enter a value for x: "))
while x != SENTINEL:
y = a * x + b
print("Result for x = " + str(x) + " is " + str(y))
x = int(input("Enter a value for x: "))
if __name__ == "__main__":
main()
What's That in Dog Years?
Everyone knows that our furry friends age at a different rate to
humans. Write a program that takes asks the user for a human age
(expressed as a whole number) and prints the equivalent dog age using
the fact that there are seven dog years per human year. Consider
defining a constant DOG_YEARS_PER_HUMAN_YEAR. You can
assume the user types in an integer age, but not necessarily that the
integer is positive. If it isn't, print an error message.
Your program should continuously ask the user for human ages until the user types 0, at which the program should end.
Here is an example of what one run of your program should look like (user input is italicized):
Enter an age in human years: -12
Sorry, please enter a positive number or 0 to exit
Enter an age in human years: 13
The age in dog years is 91
Enter an age in human years: 0
Finding Factors
Implement a program that asks the user to enter an integer, then print out all the factors of the given number, one by one. Your function should check that the entered number is greater than 0. The program should keep asking for numbers until 0 is entered.
Here is an example of what one run of your program should look like (user input is italicized):
Your number: -10
Please input a positive number
Your number: 42
1
2
3
6
7
14
21
42
Your number: 53
1
53
Your number: 0
Rock, Paper, Scissors
In 1997, a computer named Deep Blue beat world chess champion Gary Kasparov at a game of chess. In 2020, IBM has findally gained the confidence to expand its repertoire of human vs. computer games and enlisted you to write a program that allows a human player and computer to spar over a game of Rock Paper Scissors.
Each game consists of 5 rounds of Rock, Paper, Scissors. Each round
consists of you--the user--choosing whether to play Rock, Paper or
Scissors, and the computer doing the same. In this game, the user will
type 1 if they wish to play Rock, 2 if they
wish to play Paper and 3
if they wish to play Scissors.
In each round, you should follow the following steps:
- Prompt the user to enter their move (you can assume they type '1', '2' or '3'.)
-
Randomly choose either rock, paper, or scissors as the computer’s
move using the random module (remember, calling `random.randint(a,
b)` will give you back an integer between
aandb, inclusive). - Determine who wins the round. As a reminder, rock beats scissors, scissors beats paper, and paper, somewhat inexplicably, beats rock.
- Print a message reporting whether the human player won or lost and which moves each player made.
At the end of the program, you should print a message saying how many rounds you won.
Here is an example of what one run of your program should look like (user input is italicized):
Your move (1, 2, or 3): 1
It's a tie!
Your move (1, 2, or 3): 3
You Win! Scissors cuts paper
Your move (1, 2, or 3): 2
You Lose! Scissors cuts paper
Your move (1, 2, or 3): 2
It's a tie!
Your move (1, 2, or 3): 1
You Win! Rock crushes scissors
You won 2 rounds!
Estimating \(\pi\)
Write a function, estimate_pi, that estimates the value
of \(\pi\) using Python!
\(\pi\) is a mathematical constant that comes from geometric properties of a circle. Specifically, a circle that has radius \(r\) will have area \(\pi r^2\) and circumference \(2 \pi r\). \(\pi\)'s value is roughly \(3.141\dots\) and in this problem, we'll get pretty close to that value (we're shooting for 2 decimal places of accuracy)!
One nice way to estimate \(\pi\) is using the
random module. Imagine a \(2 \times 2\) square drawn on a
2D plane, centered at the origin. We can draw a circle inside this
square, with radius \(1\), centered at the origin. So far, our drawing
looks like this:
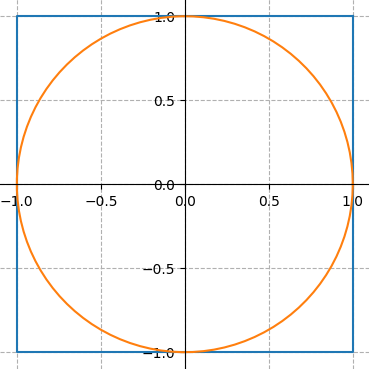
The area of the square is \(2 \times 2 = 4\) and the area of the circle is \(\pi \times 1^2 = \pi\). The circle takes up a large fraction of the square's area: to be precise, the ratio of the circle's area to the square's area is \(\frac{\pi}{4}\).
One way to think about this is that if you pick a bunch of points, randomly, inside the square, the fraction of those points that will lie inside the circle is \(\frac{\pi}{4}\).
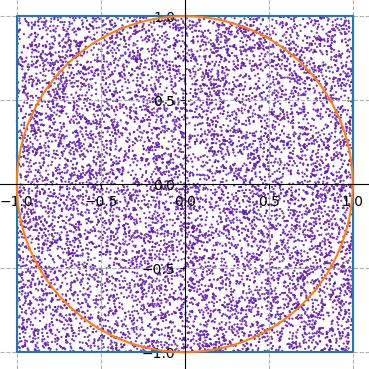

Your function, estimate_pi should randomly pick
100000 points inside the square (remember that it’s good
programming style to use constants where appropriate; consider
defining a constant NUM_POINTS = 100000).
You can pick a random point in the square by picking a random
x coordinate and a random y coordinate (both
of which should be real numbers between \(-1\) and \(1\)). Count the
number of points that are inside the circle and use that number to
calculate the fraction of points that landed inside the
circle. That number is approximately \(\frac{\pi}{4}\), so multiply
your ratio by \(4\) and print out that value as our approximation of
\(\pi\). How close did you get? What happens when you change
NUM_POINTS?
Hint: A point \((x, y)\) is inside the circle of radius \(1\), centered at the origin, if \(x^2 + y^2 \leq 1\).
Note: Your function will produce a number, not the graphs that you see in this writeup. However, these graphs were actually generated using Python and you'll be able to make images like these by the end of the quarter!
Part B: Parameters and Return Values
Once we've covered parameters and return values in class, you can re-write your solution to this problem to get some practice with for the diagnostic and calculate a more accurate value of \(\pi\)!
Re-write estimate_pi so it returns the value of \(\pi\)
that it computes and write a main function that calls
estimate_pi 100 times, in a loop. The
main function should average the values that
estimate_pi returns and print out
"The average of those estimations is:
{avg_estimation}"
where {avg_estimation} is replaced by the average of
values returned by estimate_pi.
How close is your estimation? Our estimation was accurate to four decimal places!