Ctrl+K

Alternative two sample

Alternative two sample#

Download#

Kernelizing Hotelling \(T^2\)#

library(pdfCluster)
data(oliveoil)
# let's make it a two-sample dataset (of 3 regions)
X = oliveoil[oliveoil$macro.area %in% c('South', 'Centre.North'),]
#| echo: true
South = X[X$macro.area=='South',3:10]
North = X[X$macro.area=='Centre.North',3:10]
X_1 = as.matrix(South)
X_2 = as.matrix(North)

pdfCluster 1.0-4

Olive oil data South vs Centre.North#

pairs(X, col=X$macro.area)
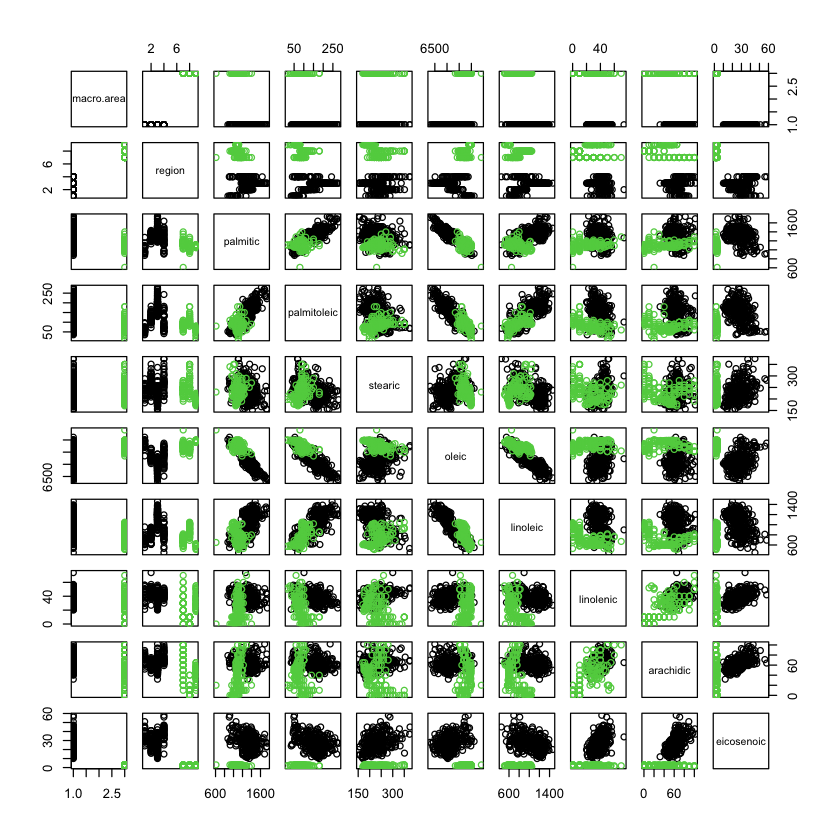
../_images/90e33b80bb570f38c158c8bec6595533dfe7ab0801f8bf190e3ac2f553993aa9.png
\[H_0:F_1=F_2\]

Gram matrices#

  • We used the term Gram matrix last time for a reason.

  • For any covariance kernel \(K:\mathbb{R}^p \times \mathbb{R}^p \rightarrow \mathbb{R}\) we could use

\[ G_{ij} = K(X_i, X_j) \]

  • Gram matrices can be computed for data that is not even Euclidean…

\[\begin{split} \begin{aligned} \text{Tr}(GP^{\Delta}) &= \frac{1}{\frac{1}{n_1}+\frac{1}{n_2}} \biggl(\frac{1}{n_1^2} \sum_{i,j=1}^{n_1} K(X_1[i,],X_1[j,] \\ & \qquad + \frac{1}{n_2^2} \sum_{i,j=1}^{n_2} K(X_2[i,],X_2[j,]) \\ & \qquad - \frac{2}{n_1 n_2} \sum_{i=1}^{n_1} \sum_{j=1}^{n_2} K(X_1[i,],X_2[j,])\biggr) \end{aligned} \end{split}\]

  • Rearranging a little

\[ \begin{aligned} \text{Tr}(GP^{\Delta}) =W_1(G) +W_2(G) \end{aligned} \]

with

\[\begin{split} \begin{aligned} W_1(G) &= W_1(G;X_1,X_2) \\ &= \frac{1}{\frac{1}{n_1}+\frac{1}{n_2}} \biggl(\frac{1}{n_1^2} \sum_{i,j=1:i\neq j}^{n_1} K(X_1[i,],X_1[j,]) \\ & \qquad \qquad + \frac{1}{n_2^2} \sum_{i,j=1: i \neq j}^{n_2} K(X_2[i,],X_2[j,]) \\ & \qquad \qquad - \frac{2}{n_1 n_2} \sum_{i=1}^{n_1} \sum_{j=1}^{n_2} K(X_1[i,],X_2[j,])\biggr) \end{aligned} \end{split}\]

  • The other term is

\[\begin{split} \begin{aligned} W_2(G) &= W_2(G;X_1,X_2) \\ &= \frac{n_1 n_2}{n_1+n_2} \biggl( \frac{1}{n_1^2} \sum_{i=1}^{n_1} K(X_1[i,],X_1[i,]) \\ & \qquad \qquad + \frac{1}{n_2^2} \sum_{i=1}^{n_2} K(X_2[i,], X_2[i,]) \biggr) \\ &\overset{H_0: (n_1, n_2) \to \infty }{=} C(n_1, n_2) E_{F_1}(K(X,X)) + O(n^{-1/2}) \end{aligned} \end{split}\]

Where does \(W_2\) come from?#

  • Let \(K(x,y)=x^Ty\) be the linear kernel. Then,

\[ E((\bar{X}_1-\bar{X}_2)^T(\bar{X}_1-\bar{X}_2)) = \|E_{F_1}(X)-E_{F_2}(X)\|^2_2 + \text{Tr}(\text{Var}(\bar{X}_1 - \bar{X}_2)) \]

  • This last term should be subtracted to get an unbiased estimate of \(\|E_{F_1}(X)-E_{F_2}(X)\|^2_2\).

  • We see then, that for any feature map \(h:\mathbb{R}^p \rightarrow \mathbb{R}^k\) leading to kernel \(K(x,y)=h(x)^Th(y)\) subtracting this \(W_2\) term yields unbiased estimate of

\[ \|E_{F_1}(h(X))-E_{F_2}(h(X))\|^2_2 \]

Maximum Mean Discrepancy Statistic (MMDS)#

  • When \(K\) is the Gram matrix of a covariance kernel, Gretton et al. (almost) propose \(W_1(G)\) as a two-sample test.

  • Specifically they propose (up to scaling)

\[\begin{split} \begin{aligned} T_{MMD} &= \widehat{MMD}({\cal H}; X_1, X_2) \\ &= \frac{1}{\frac{1}{n_1}+\frac{1}{n_2}} \biggl(\frac{1}{n_1 (n_1-1)} \sum_{i,j=1:i\neq j}^{n_1} K(X_1[i,],X_1[j,]) + \\ & \qquad \qquad \frac{1}{n_2 (n_2-1)} \sum_{i,j=1: i \neq j}^{n_2} K(X_2[i,],X_2[j,]) \\ & \qquad \qquad - \frac{2}{n_1 n_2} \sum_{i=1}^{n_1} \sum_{j=1}^{n_2} K(X_1[i,],X_2[j,]) \biggr)\\ \end{aligned} \end{split}\]

Comments#

  • This is almost \(W_1(G;X_1,X_2)\): if \(K\) is bounded by \(C'\), difference is bounded by \(C'/n\).

  • Easy to analyze their form as it is exactly a two-sample \(U\) statistic (degenerate under \(H_0\)).

MMDS in general#

  • For a class of functions \({\cal F}\) define $\( MMD({\cal F}; F_1, F_2) = \sup_{h \in {\cal F}} E_{F_1}(h(X)) - E_{F_2}(h(X)) \)$

  • When \({\cal H}\) is the unit ball in an RKHS with kernel \(K\) they show $\( MMD({\cal H}; F_1, F_2) = E_{F_1 \times F_1}(K(X,X')) + E_{F_2 \times F_2}(K(X,X')) - 2 E_{F_1 \times F_2}(K(X,X')) \)$

  • Notation: \(E_{F \times G}[h(X,X')]\) denotes expectation under \((X,X') \sim F \times G\).

  • Statistic of Gretton et al. is an estimator of \(MMD({\cal H}; F_1, F_2)\).

  • Using kernel property, it is not hard to see that the analog of (rescaled) \(\text{Tr}(XX^TP^{\Delta})\) is given by

\[\begin{split} \begin{aligned} \text{Tr}(GP^{\Delta}) &= \frac{1}{\frac{1}{n_1}+\frac{1}{n_2}} \left\| \frac{1}{n_1} \sum_{i=1}^{n_1} K_{X_1[i,]} - \frac{1}{n_2} \sum_{j=1}^{n_2} K_{X_2[j,]} \right\|^2_{\cal H} \\ &= \frac{1}{\frac{1}{n_1}+\frac{1}{n_2}} \left( \sup_{h: \|h\|_{\cal F} \leq 1} \left \langle \frac{1}{n_1} \sum_{i=1}^{n_1} K_{X_1[i,]} - \frac{1}{n_2} \sum_{j=1}^{n_2} K_{X_2[j,]}, h \right\rangle_{\cal H}\right)^2 \end{aligned} \end{split}\]

  • Like \(\widehat{MMD}({\cal H}; X_1, X_2)\) but includes this \(W_2\) term…

kernlab#

#| echo: true
library(kernlab)
kmmd(X_1, X_2)

Using automatic sigma estimation (sigest) for RBF or laplace kernel 

Kernel Maximum Mean Discrepancy object of class "kmmd" 
 
Gaussian Radial Basis kernel function. 
 Hyperparameter : sigma =  2.8390782080874e-06 


 H0 Hypothesis rejected :  TRUE
 Rademacher bound :  0.444461696552373

 1st and 3rd order MMD Statistics :  0.901532029840108 0.643725854362546

#| echo: true
kmmd(X_1, X_2, kernel='vanilladot', kpar=list())

Kernel Maximum Mean Discrepancy object of class "kmmd" 
 
Linear (vanilla) kernel function. 


 H0 Hypothesis rejected :  FALSE
 Rademacher bound :  3760.42987748469

 1st and 3rd order MMD Statistics :  798.276202069945 399126.145253863

Energy statistics#

Energy statistics#

  • We saw that Hotelling’s \(T^2\) test is essentially determined by an \(n \times n\) (case) similarity matrix \(G\):

\[ \text{Tr}(P^{\Delta}GP^{\Delta}) \]

  • A simple way to construct a similarity matrix is from a distance matrix \(D_{ij} = d(X_i, X_j)\) and setting

\[ S = \kappa I - D \]

  • Noting that \(\text{Tr}(P^{\Delta}) = 1\) suggests simply using

\[\begin{split} \begin{aligned} -\text{Tr}(DP^{\Delta}) &= \frac{1}{\frac{1}{n_1}+\frac{1}{n_2}}\text{Tr}((M_1-M_2)D(M_1-M_2)^T) \\ &= \frac{n_2n_1}{n_1+n_2} \biggl( 2 \frac{1}{n_1n_2} \sum_{i=1}^{n_1} \sum_{j=1}^{n_2} d(X_1[i,],X_2[j,]) \\ & \qquad \quad - \frac{1}{n_1^2} \sum_{i,j=1}^{n_1} d(X_1[i,],X_1[j,]) \\ & \qquad \quad - \frac{1}{n_2^2} \sum_{i,j=1}^{n_2} d(X_2[i,],X_2[j,])\biggr) \end{aligned} \end{split}\]

  • These are the energy test statistics of Szekely et al..

  • Permutations can be used to get valid tests (in package energy in R)

Energy test with Euclidean distance#

#| echo: true
library(energy)
X = rbind(X_1, X_2)
n_1 = nrow(X_1)
n_2 = nrow(X_2)
D = dist(X)
T = eqdist.etest(D, c(n_1, n_2), distance=TRUE, R=500)
T

	2-sample E-test of equal distributions

data:  sample sizes 323 151, replicates 500
E-statistic = 94382, p-value = 0.001996

Sanity check#

#| echo: true
M_1 = c(rep(1, n_1), rep(0, n_2)) / n_1
M_2 = c(rep(0, n_1), rep(1, n_2)) / n_2
P_delta = (M_1 - M_2) %*% t(M_1 - M_2) * n_1 * n_2 / (n_1 + n_2)
Dm = as.matrix(D)
c(package.value=T$statistic, byhand=-sum(diag(P_delta %*% Dm)))
package.value.E-statistic
94382.2812754321
byhand
94382.2812754317

Classification two-sample tests (C2ST)#

LDA classifier#

  • A natural classifier related to our two sample problem is to map a new test point \(x\) to the class \(i\) that (under equal sample sizes) minimizes

\[ (x - \bar{X}_i)^TS_p^{-1}(x-\bar{X}_i). \]

  • For test data \(H_0:F_1=F_2\), such a classifier should be roughly a coin flip.

  • This is the basis of the C2ST

General procedure#

  • Create label $\( Y = \begin{pmatrix} 1_{n_1} \\ 2_{n_2} \end{pmatrix} \)$ and form D=cbind(Y, X)

  • Split D randomly up in to D_test and D_train in such a way that for test data the number of cases from X_1 matches that of X_2. Let n_test denote the total number of cases of each held out.

  • Fit a classifier \(\hat{C}\) on cbind(X_train, Y_train), and evaluate its classification accuracy on cbind(X_test, Y_test).

  • Under \(H_0:F_1=F_2\), conditional on D_train the accuracy has (approximate) distribution $\( \frac{1}{n_{test}} \text{Binomial}\left(n_{test}, \frac{1}{2} \right). \)\( (This seems easiest to justify when \)X_i\( are simple random samples from large populations -- in this case given case \)x$ is selected a Bernoulli(1/2) determines which sample it finds itself in.)

References#

Contents